让深度教学发生的“四变”

■福建省厦门市民立小学 沈 铭

《义务教育数学课程标准（2011年版）》提出：数学教学的本质是推动学生思维发展。但是在实际教学中，教师往往过多地关注一些细枝末节，而忽视了某些重要的东西。在具体教学中，教师只有不断制造让学生“深度思考”的事件，才能让学生变得越来越有智慧。

一、变“单一灌输式的表层化教学”为“促进持续建构的阶梯式教学”

现代学习论认为，学习不是获得，而是建构。建构本来就是一个由易到难、由浅入深、由表及里、由分到合的持续过程。因此，学习的本质即持续的建构。例如：人教版五年级下册《找次品》，首先借助flash技术制作生动逼真的天平，通过引导学生操作生动直观的“天平”，从5个零件中找1个轻的次品，能用规范严密的语言表达“在最不利因素条件下，如果用天平从3个次品中找到其中的1个次品，只要称1次就可以找到次品。”接着让学生动手操作从9个零件中找到其中1个次品，并记录探究过程，教师通过引导学生对探究过程中的记录数据的数据观察、思考、分析，特别是观察“称第一次后能确定几个正品”，学生会发现，不管把物品平均分成几份，只有把物品平均分成三份，确定正品个数所占的百分率才是最高的（或者说能一次就确定正品的个数最多）。从而很快地就能推理出“把物品平均分成3份，能最快找到次品”，最后再从8个零件中找到其中1个次品，来体验如不能平均分的，就尽量平均分成3份的方法是最好的”（因为把物品平均分成3份，第一次能确定的正品数量最多）。通过在教师的引导下学生持续建构的探究过程，即培养学生解决数学问题的意识和能力，同时渗透“优化”这一重要的数学思想方法，以有效地提高学生的分析和解决问题的能力。

二、变“机械记忆式复述”为“参与体验式表达”

要想改变这种靠机械记忆式的学习，应当有意识地让学生积极主动地参与课堂学习中，根据学生的生活经验和学习经验，设计有针对性的学习活动去体验、探究。

例如：人教版六年级上册《圆的认识》，教师就通过把学具放在箱子里(如下图）用手去摸，谁能最快把圆摸出来？并说出摸的方法。接着让学生动手独立尝试画圆，让学生亲身感受画圆遇到的困难，再通过微课展示，规范了学生规范画圆的动作要领，从而让学生更加深刻地掌握画圆的技术要领。然后再根据教学情境要求学生动手完成：①学生画出指定位置的圆；②大小不同的圆；③画出一条以圆心为其中一个端点且另一个端点在圆上的线段；④画出一条经过圆心且2个端点在圆上的线段，从而让学生在实际体验过程中掌握圆心确定位置、半径（直径）确定圆的大小、认识半径和直径这些圆的特征，最后再通过在教师甩动短绳制造的圆中寻找圆心和半径中进一步巩固对圆的认识。

三、变“真理传承式的教学”为“思辨创新式的教学”

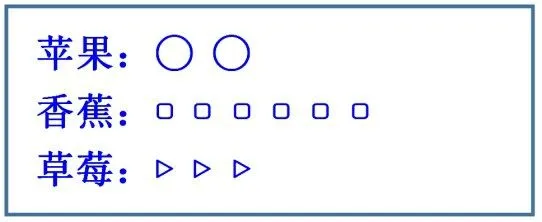
教育不仅仅是简简单单的社会文化传承、复制，应该说新时代的教育是肩负传承与创新的共同体。例如：人教版三年级上册《倍的认识》，三年级大部分学生还停留直观思维阶段，要理解“倍”这相对抽象的概念还是比困难的。因此，利用课件的直观具体这一优越性，在课件的设计就有意识地把苹果按2个一组的摆放，有意识地向学生渗透“1倍量”意识。再引导学生通过观察、思考后不仅能说出香蕉比苹果多4个以外（或苹果比香蕉少4个），还能通过观察课件在教师的引导下说出：把2个苹果看作1份，香蕉的根数有这样的3份。此时教师就可以适时地引出：我们就说香蕉的根数是苹果个数的3倍。当学生初步建立了“倍”这这一概念后，此时，通过追问：如果要使香蕉的根数是苹果的4倍，应该怎么办？从而让学生明白香蕉根数是苹果的几倍，关键是看香蕉的根数有几个“1倍数”。当学生理解“倍的意义”后，再呈现，追问：同样是6根香蕉，为什么它是苹果个数的3倍，却是草莓个数的2倍呢？引导学生通过对比思辨得出结论：因为“1倍数”的个数不一样，也就是要知道香蕉是2种水果的几倍，必须先确定“1倍数”有几个，然后看香蕉有几个这样的“1倍数”，就可以确定香蕉是它们的几倍。从而给学生建立“倍的意义模型”：先确定1倍数有多少，再看另一个量有几个1倍数，就知道另一个量是1倍数的几倍。

四、变“单一的知识传授”为“建立关联的知识体系”

新课程改革特别强调对学生思维能力的培养，而在课堂教学上有意识地让学生从整体上把握知识就是非常重要的一个环节。如果在课堂教学的时候，着眼于学生的最近发展区，有意识地借助新旧知识连接点，通过观察、对比、分析，探究新旧知识的异同点，同时有意识地引导学生勾连与此关联的同类知识进行对比，总结其共性的知识内涵。

例如：人教版五年级下册《异分母分数加、减法》，在教学时，大部分教师都会以灌输式的方式进行教学，对学生说，因为和的分数单位不同，所以不能直接相加减，所以要通分，也就是把分母不同的分数转换成分母相同的分数再进行计算。但还是有部分学生不理解“分数单位不同”的真正内涵是什么意思。如果此时借助“数形结合”让学生用+来表示这个算式，就能很清楚地诠释“分数单位不同”的含义了。当学生在掌握异分母分数加、减法的计算方法后，再实时出现159+27、159-2.7这四种计算，让学生通过观察比较其计算方法上有什么相同点，学生很快就能发现整数加法列竖式要个位对齐、小数减法在列竖式要小数点对齐、异分母分数要先通分再计算，都是要为了计数单位相同，才能直接相加减，从而建立第一级计算的本质内涵知识体系。只有“现在的我”与“过去的我”在教材解读、教学策略、教学方法、教学理念上进行对比与改变，才能引导学生的学习更本质、更深入、更高效，使学生经历“真学”“会学”“乐学”，从而让我们的教学真正发生。