让学生“动”起来，让数学课堂“活”起来

何君悦

【摘要】一堂“活”的数学课就像摆在眼前的珍珠那样耀眼，就像一把能开启智慧之门的金钥匙。“活”的课堂主要指教师的教学方法手段要灵活，学生的思维要鲜活，课堂的气氛要快活。当代数学老师不仅要思维敏捷、学识渊博，还要魅力四射、饱含激情，更要有新时代背景下教育的新理念，要让学生“动”起来，让课堂“活”起来。

【关键词】八年级数学上册;动;活

数学新教材形式多样，再也没有像旧教材那样直奔主题的例题了。这无不告诉我们，当代数学老师不仅要思维敏捷、学识渊博，还要魅力四射、饱含激情，更要有新时代背景下教育的新理念，要让学生“动”起来，让课堂“活”起来。

一堂“活”的数学课就像摆在眼前的珍珠那样耀眼，就像一把能开启智慧之门的金钥匙。“活”的课堂主要指教师的教学方法手段要灵活，学生的思维要鲜活，课堂的气氛要快活。十几年的教学经历，告诉我具备了这三“活”，才能让学生积极主动地参与数学课堂，才能使学生全身心地动起来，从中感受到学习数学的乐趣，甚至是数学知识的掌握，学生认识水平、数学素养、人文精神的教育和情感个性的协调发展才能实现。让学生主动积极地参与课堂是新课程理念的要求，也是我一直以来探寻的目标，以下是我在八年级数学上册教学片段中采取的一些措施。

一、创设情景，让学生“心”动

俗话说：“良好的开端是成功的一半。”如果教师在教学过程中设法多创设具有针对性、趣味性、创造性的活动情景，引起学生发自内心的去学习知识，活动中常会起到意想不到的效果。

1.利用新闻导入。比如，在《等腰三角形的判定定理》教学中，我是用如下的方式进行课题引入的。利用课件显示：远处一片浩瀚的海洋，风平浪静，一所游轮正在航行，忽然狂风大作，游轮上下起伏，屏幕显示问题：2005年7月29日，一艘远洋巨型游轮正在我国东南沿海海面A处航行，突然强烈的海啸向他们猛然袭来，情况万分紧急，船长立即向B、C两处的两艘救生船发出求救信号，请求救援。当时测得∠B=∠C，问如果这两艘救生船以同样的速度同时出发能不能大约同时赶到出事地点实施救援？（不考虑风浪因素）以这样贴近生活紧急救助问题形式呈现，与学生心灵碰撞，可激发学生的求知欲。

2.故事激发兴趣。比如在探索最短路径问题时，我是用以下故事引入课题的。“相传古希臘亚历山大里亚城里有一位久负盛名的学者，名叫海伦。一天，一位将军专程拜访学者，求教一个百思不得其解的问题：从图中的A地出发，到一条笔直的河边l饮马后到B地。到河边什么地方饮马可使他所走的路程最短？”数学来源于生活又服务于生活。本就是生活中的问题，可如果用典故的形式呈现更可以达到激发学生兴趣的效果。

3.游戏导入，学习深刻。在学习《全等三角形及其性质》时，我设计了这样两个游戏：①找朋友。上课时我送给每个同学一个三角形，请他们快速在自己周围找朋友，谁手中的三角形能与自己的完全重合，谁就是自己的好朋友。

②我们做游戏时把双手五指重叠在一起，两个大拇指、两个食指、两个中指……分别对齐来理解对应关系，那么怎么将两个全等三角形重叠在一起？如果重叠的元素理解为对应的话，那么它们会有哪些对应元素？分别叫什么名称？

二、利用日常行为习惯、礼仪情感编成话剧让学生“动”起来

学生在学习《多项式乘法》时，总是会漏乘或多乘甚至是符号错误。因此，在教学中设计了这样一个活动：将班上一个小组的七八名同学抽出来分成两组，每组的同学相当于一个多项式，而每个同学就是这个多项式里的项，然后两组的同学各自拿着代表项排成队，一组不动，另一组按顺序一一和不动的那组握手，每握手一次计算出来的项记录好才进行下一次或下一个的握手。观摩后，班上其他各组按先布置好的多项式演示一遍，让人人参与、亲身经历以达到学习的最大目的。事实上，学生只要回想当时表演的情境，多项式乘法运算就不再头昏脑胀啦，计算就也条理了，显然很少出错。

三、动手操作、自主探究、合作交流，让学生成为课堂的演绎者，让课堂“活”起来

教“活”学“活”，课堂气氛怎能不“活”？教师引导学生“探究”，学生全身心投入思考;教师鼓励学生“尝试”，学生就不断开拓创新;教师激励学生“挑战”，学生就思维飞扬。

《等腰三角形的判定定理》教学中，不仅仅是学会定理，运用定理解决问题，更重要的是要使学生经历探究的过程，培养学生的动手操作能力，合作意识和创新意识。因此整个过程中要注意让学生在动手操作、自主探究，充分发挥学生的主观能动，将学习过程切实变成学生主动获取知识的过程。我是组织以下几环节进行教学。

1.动手操作，合作探究，猜测结论

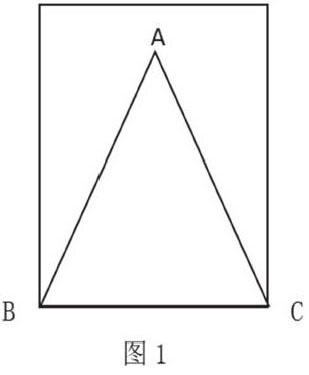
（1）布置学生分组进行操作剪纸，让学生利用量角器和剪刀剪出如图1所示的两个相等的角形成一个三角形ABC，然后让学生度量AB和AC的长，在这个过程中应留给学生足够的时间思考、探索、交流，教师要巡堂加以指导、点拨，及时帮助学生解决所遇困难。

（2）小组汇报交流，各小组分别到讲台展示自己剪出的三角形，并指出其中的线段大                          小关系

（3）启发点拨、猜测结论：在三角形中，如果有两个角相等，那么这两个角所对的边也相等。

2.分析比较对比证明

（1）回顾等腰三角形的性质，引导学生比较自己得出的结论与等腰三角形的性质定理的关系，此时可复习命题，逆命题、定理的概念。

（2）进一步启发学生回顾上节课等腰三角形性质定理的

证明方法：

a作顶角的平分线，

b作底边上的高线，

c作底边上的中线，

让学生试着类似的方法来证明判定定理，但辅助线的作法要有所改变

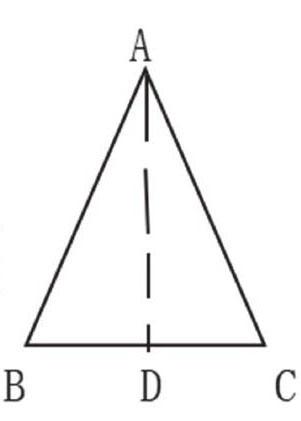
d作∠A的平分线AD，

e作BC边上的高线AD，

f作BC边上的中线AD，

通过学生的分析、讨论，学生会发现e、d可以证明判断定理，而f不能证明它。这也是判定定理和性质定理在证明途径方面的区别。

（3）汇报交流，导出定理。

总之，在教学中教师要通过设计丰富多彩的活动，还要敢于、舍得让学生去做活动，引导学生积极用眼、用口、用手、用脑，在活动中启动多种感官去获得直接经验，让学生在实践和体验中努力思考提高解决问题的能力，只有这样才能激发学生学习数学的兴趣，培养学生动手的欲望和操作的能力，让学生发自内心的学习数学，让学生学得轻松、乐学、爱学，“让学生在数学课堂上始于快乐，止于智慧”。

【参考文献】

[1]人教版八年级数学（上册）.

[2]中学课程辅导（教学研究），2017（21）.

[3]一堂活的语文课[J].小说月刊， 2018（2）.