斜拉索风雨振影响参数的理论研究

2020-08-27陈冬剑胡云天

结构工程师 2020年3期

陈冬剑毕伟胡云天

（1.江苏省建筑工程质量检测中心有限公司，南京210000；2.邢台职业技术学院，邢台054000；3.中交公路规划设计院有限公司，北京100088）

0 引言

当前斜拉桥在设计阶段就考虑拉索的风致振动危害问题，其中以风雨振最为突出，很多大跨度斜拉桥已经将风洞试验研究列于设计文件之中，然而由于拉索长度制约，风洞研究普遍采取节段拉索进行试验以获得相应的气动力试验数据，故有必要进行节段拉索风雨振理论模型的推导，给出相关分析结果以供风洞试验研究进行参考比对。

在理论分析方面，Yamaguchi［1］建立了首个弯扭耦合的两自由度节段拉索模型；彭天波［2-3］建立了含上下水线的三自由度节段拉索模型；杜晓庆［4］通过试验获得了拉索和水线平均气动力系数建立了更精细的两自由度节段拉索模型；李暾［5］研究了水线与拉索表面的相互作用力，确定了PE材料表面的库伦阻尼力约为0.062 7 N/m，并根据Prandtl 边界层理论确定了黏滞线性阻尼力约为1 Ns/m2，相互作用力的确定使得风雨振节段拉索模型更加完善。

然而，在当前日趋完善的风雨振模型下，斜拉索与水线的参数对风雨振影响规律的定量研究还不多，基于此原因本文开展了相应的研究工作。

1 风雨振节段拉索模型

1.1 理论模型推导

本文采用运动水线两自由度节段拉索风雨振理论模型，结合国内外当前对于风雨振的认知，可作如下假设：

（1）考虑斜拉索面内振动，忽略面外振动；

（2）计入上水线影响，下水线稳定性可不计；

（3）水线的形状、大小在风雨振时保持不变；

（4）水线的质量远远小于拉索的质量；

（5）准定常假设成立。

风雨振斜拉索理论模型的示意图如图1 所示，其中图1（a）给出了节段拉索空间位置示意图。根据图1（b）可建立拉索沿面内方向的振动微分方程，其表达式为

由图2 可建立上水线沿拉索表面作周向运动的微分方程：

图1 风雨振模型Fig.1 Rain-wind induced vibration model

式（1）和式（2）中：Mc为单位长度拉索的质量；m为单位长度水线的质量；c为拉索阻尼系数；k为拉索刚度系数；g为重力加速度分别为斜拉索在面内发生振动的位移、速度和加速度；θ0为水线的初始位置分别为水线的角位移、角速度和角加速度；R为拉索截面半径；cr为黏滞线性阻尼系数；文献［6］将水线振动的弹性回复力kθ假设为库仑阻尼力F0；sgn（）为符号函数；FL为拉索受到的平均气动升力；FD为拉索受到的平均气动阻力；fτ为水线受到的平均气动力沿拉索表面切线方向的分量；FN为斜拉索表面与水线之间的正压力；α为拉索倾角。

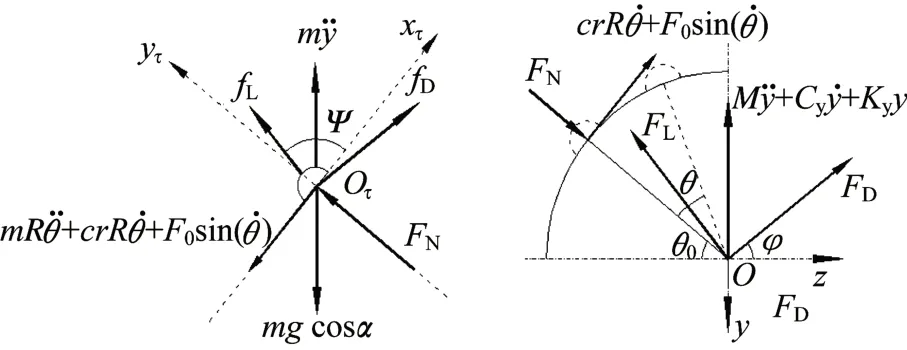
图2 相互作用力示意图Fig.2 Interaction force diagram

由图1（a）可获得相对风速Urel与水平风速的夹角φ值为

式（3）中：

式中：β为风偏角；U0为来流风速。

Urel相对风速的大小为

式（1）中，拉索受到的平均气动力为

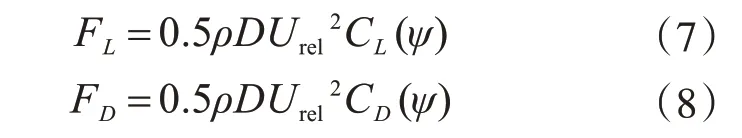
式（2）中，水线受到的平均气动力沿拉索表面切向的分量fτ为

式（7）-式（9）中：

式中：D为斜拉索的直径；CL为拉索的平均气动升力系数；CD为拉索的平均气动阻力系数；B为水线表面圆弧直径；fL、fD分别为水线受到的平均升力和阻力；cl、cd分别为水线平均升力和阻力系数；ρ为空气密度。

在式（1）中，根据假设（4），由于单位长度水线质量m、正压力FN、库仑阻尼力F0和黏滞线性阻尼力crRθ˙的值很小，在方程中可以忽略不计。因此式（1）可以化简为

式中：ξ为拉索的阻尼比；ω为拉索振动圆频率。

拉索风雨振的求解即转化成对于式（2）和式（11）的微分方程求解。

1.2 拉索风雨振响应

拉索风雨振的求解算法采用四阶龙格库塔法。其中拉索与水线的气动力系数选取杜晓庆在节段拉索风洞试验中粘贴固定人工水线进行试验测得的数据［4］。节段拉索参数、水线参数以及振动初始条件见表1。

经计算获得拉索在振动后期振幅与风速的关系如图3 所示，可见拉索风雨振呈现出明显的“限速限幅”特性且发生在较低的风速下，这与当前拉索风雨振的模拟与实测结果相符合。在当前工况下，拉索风雨振出现三个平稳段和两个起振风速区间。

图4 给出了拉索在三个平稳段和两个起振风速区间内某一风速下的振动时程，由图可见平稳段的拉索振幅由于自身阻尼作用振动呈现衰减形式，而在两个起振风速区间内，拉索发生了稳定持续的大幅振动。

表1 参数取值Table 1 Parameter value

图3 拉索振幅与风速的关系Fig.3 Relationship between cable amplitude and wind speed

将起振风速区间内拉索与水线的振动经快速傅立叶变换得到其幅频如图5 所示，拉索以其固有频率发生振动，水线振动的主要频率与拉索固有频率相一致，同时夹杂着少量的倍频成分。

2 拉索风雨振参数影响分析

2.1 阻尼比的影响

对于拉索阻尼比的变化对拉索振幅的影响如图6 所示，拉索最大振幅随着阻尼比的增加而显著地减少，当阻尼比达到0.6%后拉索基本不发生共振。与此同时可见，拉索阻尼比的变化并不会改变风雨振起振风速区间。

2.2 黏滞线性阻尼系数的影响

图4 拉索风雨振时程图Fig.4 Wind and rain vibration time history

对于拉索和水线之间的黏滞线性阻尼系数cr的推导可参考文献［5］采用了Prandtl 边界层理论确定了cr约等于1 Ns/m2，拉索最大振幅随着黏滞线性阻尼系数的增大会经历着由小变大，再由大变小这样的起落过程，其中cr=1 Ns/m2振幅最大（图7），同时随着黏滞线性阻尼系数的增大对第一起振风速区间的影响很大，但对第二起振风速区间的改变不显著。

2.3 单位长度拉索质量的影响

图5 拉索与水线的幅频图Fig.5 Amplitude-frequency plot of cable and waterline

图6 阻尼比对振幅的影响Fig.6 Effect of damping ratio on amplitude

图7 阻尼比对振幅的影响Fig.7 Effect of damping ratio on amplitude

在进行节段拉索风雨振的风洞试验亦或是利用节段拉索理论模型进行计算时，若采用单位长度拉索在实际情况下的质量，其振幅将小于实际连续拉索振幅，因而节段拉索模型通常选取实际连续拉索的折减质量，折减后的单位长度拉索质量约为实际质量的1/5～1/10。对于单位长度拉索质量Mc的变化对振幅的影响如图8 所示，可见拉索最大振幅随着单位长度质量的增加而减少，其变化规律类似阻尼比，拉索单位长度质量的变化并不会改变风雨振起振风速区间。

图8 单位长度拉索质量对振幅的影响Fig.8 Effect of mass of cables per unit length on amplitude

3 风雨振水线参数影响分析

3.1 水线表面圆弧直径的影响

对于水线参数的取值，目前尚未见有文献对水线的大小、形状和质量给出明确的确定方法。针对水线表面圆弧直径B，参考文献［4］的假定取值13.5～16.4 mm，通过图9 可知，B的增大对拉索振动最大幅值的影响近似成线性递减，随着B的增大风雨振的风速区间大小基本不变，但风雨振区间出现的风速发生了提前。

图9 水线表面圆弧直径对振幅的影响Fig.9 Effect of arc diameter on waterline surface on amplitude

3.2 单位长度水线质量的影响

关于单位长度水线质量m的取值，不同学者［4，7-9］都有所不同，本文考虑由 0.01～0.06 kg/m 变化。而文献［10］指出观测到的风雨激振的风速基本在5～20 m/s，图10 给出了该风速段下单位长度水线质量和拉索最大振幅的关系，可见单位长度水线质量m在0.03 kg/m 以下时拉索振幅较小，m在 0.04～0.06 kg/m 时，拉索在风速 14～20 m/s 时出现了更大的振幅，水线质量的增加同时也会提高起振风速，并且风雨振的风速区间变得更大。