基于人工地震波的铅芯橡胶支座等效线性化模型研究

杨 春

（上海经纬建筑规划设计研究院股份有限公司，上海200090）

0 引 言

建筑或桥梁结构隔震设计的原理是通过设置水平隔震支座，延长结构自振周期，削弱地震能量传递，减小地震作用时的结构响应，从而在最大程度上保障结构的抗震安全性。地震作用下，隔震支座进入非线性受力状态，一般情况下应通过非线性时程分析以获得精确解。然而，隔震结构的地震反应特征近似于单自由度体系，理论上采用反应谱分析方法也可得到比较准确的结果。使用反应谱方法的前提条件是结构为线弹性体系，因此，将隔震支座的非线性特征做等效线性化是反应谱分析首先需要解决的问题。

隔震支座等效线性化的原理是在支座水平剪切变形量相同的条件下，用一个等效线性系统的刚度和阻尼比来反映支座屈服后的刚度退化和弹塑性耗能，从而将非线性分析问题转化为线性分析问题。鉴于其物理意义明确、应用简便的特点，我国以及国外的抗震规范都引入了等效线性化方法。目前，已提出的等效线性化方法可归为两类：一类是从概念推导出的理论模型；另一类是由统计分析回归得到的经验模型。总体来说，经验模型的准确度比理论模型更高。但是经验模型的应用也是有局限性的，不可能对任何设计输入地震波都能预测得到比较准确的计算结果，因为现有的经验模型是由数量有限且具有某种反应谱特征的天然地震波“训练”得到的。然而，我国的桥梁工程设计中一般采用人工合成地震波进行抗震设计，人工地震波与天然地震波在反应谱特征上存在显著差异，现有经验模型的预测准确性必然会降低。基于上述原因，本文以抗震规范设计加速度反应谱的合成地震波作为“训练”样本，统计回归出一种在我国桥梁工程适用性更强的铅芯橡胶支座等效线性化经验模型。

1 理论推导

1.1 经典等效线性化模型回顾

1）AASHTO规范模型

美国的 AASHTO 规范［1］，以及我国的桥梁抗震设计规范［2］均采用了割线刚度法，等效刚度为最大水平位移对应的割线刚度，等效阻尼比按最大滞回耗能相等的原则确定。

2）JPWRI规范模型

日本的JPWRI规范［3］仍采用割线刚度法的形式，但等效刚度与等效阻尼比按0.7倍最大水平位移确定。

3）CALTRANS规范模型

美 国 加 州 规 范 CALTRANS［4］采 用 了 Hwang等［5］在 Iwan 模型［6］基础上发展起来的经验模型，该模型适用于延性比μ≤8、屈服刚度折减系数α=0.05的情况。

4）Hwang模型

Hwang 等［7］又在 CALTRANS 规范模型的基础上提出了适用于较大屈服刚度系数（α≥0.05）和延性比（μ≥8）的经验模型，拓宽了等效线性化方法的适用范围。

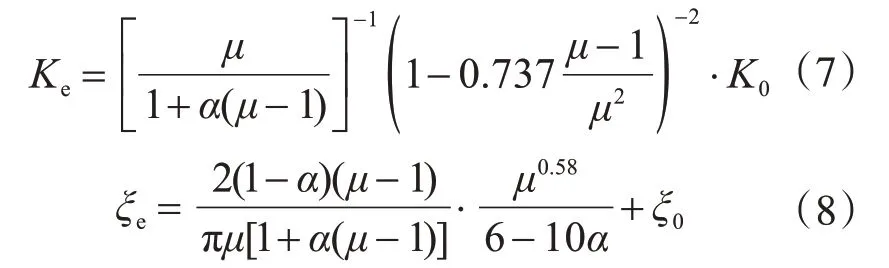
以上模型公式中，μ为支座水平位移延性比，α为支座屈服刚度折减系数，Ke为支座的等效水平刚度，ξe为支座的等效阻尼比，K0为支座的初始水平刚度，ξ0为支座其他耗能的综合阻尼比，一般取0.05。需要说明的是，综合阻尼比ξ0是支座的任何位移阶段都存在的，而黏滞阻尼比是支座进入弹塑性位移后才附加进去的，所以将等效阻尼比表示成黏滞阻尼比与综合阻尼比之和的形式。

1.2 本文等效线性化模型

本文等效线性化模型的推导仍以CALTRANS模型的原理为基础，即认为等延性比条件下的弹塑性位移谱可由一个线弹性系统的位移谱来近似，该线弹性系统就是所求的等效线性系统，其系统参数可通过优化算法进行识别。以下介绍具有双线性恢复力模型的铅芯橡胶支座的等效线性化推导过程。

系统参数识别优化算法的误差函数如下：

式中：Sd为等效线性系统的位移谱；Sμ是延性比为μ的双线性系统的弹塑性位移谱；T0，i为双线性系统初始自振周期；n为位移谱的周期点数；β1=Te/T0为自振周期比，β2=ξe为等效线性系统阻尼比，β1与β2即为所要识别的参数。

我国规范［8］推荐的标准铅芯橡胶支座的屈服刚度折减系数α约为0.155，综合阻尼比取值为 0.05［9］。

为了使等效线性化模型具有普遍适用性，识别出的参数具有统计平均意义，需要由各种特征的人工地震波计算出Sμ的目标样本。根据我国抗震设计规范对不同烈度区、不同级别地震大小的定义，选取了覆盖6～9 度区设防地震和罕遇地震的7种地震动峰值加速度0.05g、0.1g、0.125g、0.2g、0.22g、0.4g和 0.62g。另外按均匀分布的原则选取了7 种场地特征周期，分别为0.25 s、0.35 s、0.45 s、0.55 s、0.65 s、0.75 s 和 0.9 s。共计49 条地震波。图1 绘制了其中一条峰值加速度0.2g，特征周期0.45 s 的地震波时程曲线及其加速度反应谱。

图1 人工合成地震波（0.2 g-0.45 s）Fig.1 Artificial earthquake wave（0.2 g-0.45 s）

隔震后的桥梁结构初始自振周期通常不高于2 s，因此位移谱周期范围取 0.2～2 s，间隔 0.1 s。Sμ的目标样本应考虑到出现支座大位移的可能性，故取用了17 种延性比：2、4、6、8、10、12、14、16、18、20、24、28、32、36、40、45和50。

本文的系统参数识别采用修正的高斯-牛顿算法［10-11］，搜索迭代公式为

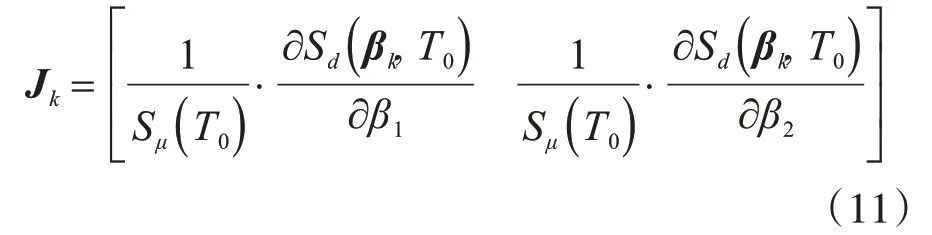
根据以上算法，图2给出了在图1地震波作用下延性比μ分别为8、28和50的系统参数，以及相应的弹塑性位移谱与等效弹性位移谱曲线。

图3 汇总了前述49 条地震波作用下，识别出的关于17 个延性比的等效线性系统参数，其中每个点对应于一条地震波和一个延性比。根据识别出的系统参数及其分布特征，分别拟合出周期比、等效阻尼比与延性比的关系曲线，如图3 中实线所示。周期比与等效阻尼比的拟合公式分别为式（12）和式（13），由式（12）可进一步得到等效刚度Ke的计算公式（14）。

前述经典模型与本文模型在不同延性比时的等效刚度比和等效阻尼比如图4 所示。由图可见，各模型的等效刚度比变化趋势比较相似，本文模型的等效刚度比与Hwang 模型更为接近；各模型的等效阻尼比变化趋势差异较大，除CALTRANS 模型外均呈先增后减的变化趋势，本文模型的等效阻尼比与Hwang 模型更为接近，但在中、高延性比范围内较Hwang模型更大。

图2 弹塑性位移谱与等效弹性位移谱比较Fig.2 Comparison between inelastic spectrum and identified equivalent elastic spectrum

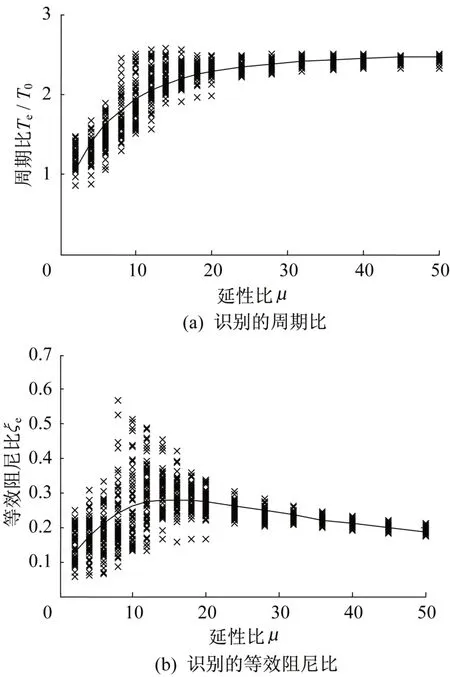
图3 等效线性系统参数拟合曲线Fig.3 Parameter fitting curve of equivalent linear system

图4 各种等效线性化模型对比Fig.4 Comparison among various equivalent linear models

2 算例验证

为了验证本文推导的等效线性化模型的适用性，下面以一座3×30 m 小箱梁桥的铅芯橡胶支座隔震分析作为数值算例，结构有限元模型见图5。上部结构为4 片小箱梁，梁距3 m；下部结构盖梁截面2×2.5 m，墩柱截面1.6×2.5 m，高度5 m；承台高度2 m。小箱梁混凝土强度等级C50，盖梁C50，墩柱C40，承台C30。铅芯橡胶支座竖向刚度1×108kN/m，水平初始刚度20 600 kN/m，屈服刚度折减系数0.155，水平屈服承载力134 kN。桩基对桥梁的约束采用6×6刚度矩阵模拟。输入地震波选用了3 条新合成的人工波和2 条天然波。计算分析在Sap2000有限元软件上完成。

图5 桥梁隔震计算模型Fig.5 Numerical model of isolated bridge

表1 汇总了5 条地震波输入时的隔震支座最大水平位移预测结果。由表可见，本文等效线性化模型的预测结果均优于Hwang模型。这说明本文模型不仅适用于人工合成地震波的隔震分析，对于部分天然地震波的隔震分析也是适用的。

表1 等效线性与弹塑性位移结果比较Table 1 Comparison between equivalent and inelastic displacement solution

3 结 论

本文采用我国抗震规范的设计加速度反应谱合成的地震波建立了一种在桥梁工程中适用性更强的铅芯橡胶支座的等效线性化经验模型，并用数值算例验证了该模型的有效性，得到以下结论：

（1）同属于经验模型，用人工地震波拟合的等效线性化模型与Hwang 模型在中、高延性比区段内存在显著差异，这说明隔震支座的等效线性化模型不仅与支座自身的力学参数有关，还受地震加速度反应谱特征的影响。因此，在实际工程中应注意合理选择等效线性化模型。

（2）本文模型主要用于按我国抗震规范的设计加速度反应谱所做的隔震设计，支座水平位移预测的准确度优于Hwang 模型，而且对部分天然地震波的隔震分析也有较好的预测结果。