钢筋混凝土梁的时变可靠度实用分析方法
2020-08-27蒋利学王卓琳
蒋利学 王卓琳
(上海市建筑科学研究院有限公司上海市工程结构安全重点实验室,上海200032)
0 引 言
我国国家标准《工程结构可靠性设计统一标准》(GB 50153—2008)[1]和《建筑结构可靠度设计统一标准》(GB 50068—2001)[2]将结构极限状态分为承载能力极限状态和正常使用极限状态两类,并明确将耐久性划入正常使用极限状态范畴。新版的《建筑结构可靠性设计统一标准》(GB 50068—2018)[3]考虑了结构耐久性的影响,将结构极限状态分为承载能力极限状态、正常使用极限状态和耐久性极限状态。《混凝土结构耐久性评定标准》(CECS 220:2007)[4]确定三种耐久性极限状态:钢筋开始锈蚀,钢筋保护层锈胀开裂,混凝土表面出现可接受的最大外观损伤。显然,这里的耐久性极限状态是限定在正常使用极限状态范畴的。对大多数建筑结构而言,将耐久性问题设定在适用性范畴的目标是合适的。但某些情况下耐久性问题可能演变为结构安全性范畴的问题,如:对于临时性建筑、仓库等使用要求不高的建筑,使用数年后拟拆除的建筑等,人们往往可以接受对影响正常使用的问题不作维修、允许其超越正常使用极限状态但安全风险仍可控的状况。这时,评定后续使用年限内耐久性退化是否会影响结构安全性是一项最重要的任务。
工程实践表明,由于我国建筑结构设计规范正式提出耐久性设计要求的时间不足20 年,部分既有建筑的耐久性措施不足,人们对结构服役阶段的正常检查维修工作重要性认识不足、措施不到位,部分老旧建筑的服役时间已远超过其原设计使用年限,部分既有建筑由于经济或其他制约因素长期年久失修等,确有不少既有建筑已出现钢筋严重锈蚀、保护层剥落、箍筋锈断、砖墙严重风化等耐久性损伤,这些损伤不仅严重影响正常使用,而且对结构安全性也造成了显著影响。这在既有结构评定与加固的工程实践中经常遇到。
某些使用环境恶劣的结构,在新建结构设计或既有结构改造设计时,采取耐久性防护措施技术难度大或经济性不合理,这时可采取提高结构安全储备的措施以弥补耐久性的不足。
一般而言,多数材料耐久性引起的抗力退化有先慢后快的非线性发展规律。以一般大气环境下钢筋锈蚀引起的混凝土构件性能退化为例,其退化过程大致分为三个阶段:第一阶段,混凝土碳化引起钢筋开始脱钝锈蚀前,抗力一般不退化;第二阶段,钢筋脱钝至保护层胀裂前,一般钢筋锈蚀率不大,抗力降低较少,但对于钢筋直径较小且保护层厚度较大的墙、板类构件,钢筋截面损失率可能达10%以上[4],梁、柱类构件的箍筋锈蚀引起保护层开裂时的截面损失率也可能达15%以上[5],这些构件的抗力退化已不容忽视;第三阶段,保护层胀裂后,钢筋锈蚀和抗力退化速率明显加快。更为重要的是,钢筋锈蚀不仅引起钢筋截面损失,还引起钢筋力学性能降低、与混凝土的粘结性能下降,构件承载力进一步下降,甚至引起构件破坏模式的改变。这种性能退化更加体现出先慢后快的非线性发展规律[6-7]。文献[8]通过对北京地区民用建筑地上结构的调查,确定钢筋锈蚀引起的抗力衰减函数可用一条三次曲线表达,即随着服役时间的增长,不仅抗力退化速率加快,而且抗力退化的加速度也是随时间增长的。可见,耐久性问题对一般新建结构可能并不突出,但对服役时间较长的既有结构,耐久性引起的抗力退化不仅影响正常使用,还可能直接影响结构安全性。
国内外已有不少研究考虑抗力退化的结构可靠度分析和寿命预测的成果。但由于同时考虑抗力和荷载效应时变性的可靠度分析模型十分复杂,多采用蒙特卡罗或改进蒙特卡罗方法[8-11]进行计算,计算工作量很大,难以在一般工程中推广应用。姚继涛提出的时段分析法[12]不同于蒙特卡罗或改进蒙特卡罗方法,但计算过程同样十分复杂,直接用于工程计算尚有不少难度。作者利用不考虑抗力退化时结构的累积失效概率与服役年数成正比的规律,当评估使用年限缩短时,直接对累积失效概率进行线性折减确定抗力需求折减系数,以此代替荷载效应折减;采用同时考虑空间和时间分布上的抗力平均值,将结构抗力随机过程退化为随机变量。以此为基础,建立了既有结构基于评估使用年限的可靠度评定实用方法[13]。
本文以钢筋混凝土梁的受弯承载力为研究对象,考虑服役期内的抗力退化和评估使用年限缩短,采用近似方法对其进行时变可靠度分析,并对近似法与可靠度法的计算结果进行了比较。
1 不考虑抗力退化时结构累积失效概率的发展规律
以按我国现行规范[14]设计的钢筋混凝土梁的受弯承载力为例,不考虑抗力退化,分析其在服役期的累积失效概率发展规律。根据作者的前期研究,按照我国标准及相关统计参数计算,恒荷载+风荷载组合下的构件可靠度普遍低于恒荷载+楼面活荷载组合下的可靠度;另一方面,我国相关标准对风荷载提供了最短重现期为1 年的统计数据,而对楼面活荷载仅提供最短时长为10 年的统计数据,因此恒荷载+风荷载组合下更具有精细化分析的条件。基于上述两点,本文选择恒荷载G与风荷载W组合下的钢筋混凝土梁承载力进行分析。风荷载与恒荷载标准值的比值ρ=Wk/Gk,取ρ=0.1、0.25、0.5、1.0、2.0五种工况。荷载和抗力的统计参数和分项系数见表1。设QT=maxQ(t),t∈[0,T]为设计使用年限T内可变荷载效应Q(t)的最大值随机变量,则当不考虑抗力退化时,承载能力极限状态的功能函数为

按照我国统一标准[1,3]和荷载规范[15],风荷载采用极值I 型分布模型。按照表1 所示统计参数计算,不同设计或评估使用年限下的风荷载最大值随机变量QT的统计参数见表2。
用JC 法计算构件在不同服役年数下的可靠指标,并将其换算为累积失效概率,得到不考虑抗力退化时累积失效概率随服役年数增长而发展的曲线见图1。

表1 荷载和抗力的统计参数和分项系数Table 1 Statistical parameters and partial coefficients of load and resistance

图1 不考虑抗力退化时累积失效概率的发展规律Fig.1 Development law for cumulative failure probability without consideration of resistance degradation
由图1 可见:除ρ=0.1 的工况,其余各种工况下的累积失效概率与服役年数基本成正比;T=50 a(a代表年)时的可靠指标越小,则其对应的累积失效概率越大,直线的斜率越大(图中以ρ=2.0时的斜率最大)。ρ=0.1 时,Pf-T曲线为幂函数曲线,即服役初期累积失效概率增长较快,后期增长逐渐减慢,这是可变荷载比例过小引起的。可以设想,如该构件仅受永久荷载作用,则它的Pf-T曲线为一条水平直线。虽然ρ=0.1时并未呈现“累积失效概率与服役年数成正比”的规律,但考虑到按我国现行设计规范[14],ρ=0.1时永久荷载效应起绝对控制作用,对既有结构评定而言,由于永久荷载可通过现场实测确定,其不确定性大幅度降低,分项系数γG取1.3 时可靠指标有较大余量,在“累积失效概率与服役年数成正比”的假定下对累积失效概率进行线性折减确定抗力需求折减系数,不会引起实际可靠度不足。如评估使用年限为5年时,抗力需求折减系数取0.9[13],则相当于永久荷载分项系数取1.3×0.9=1.17,其荷载效应仍具有足够的保证率。
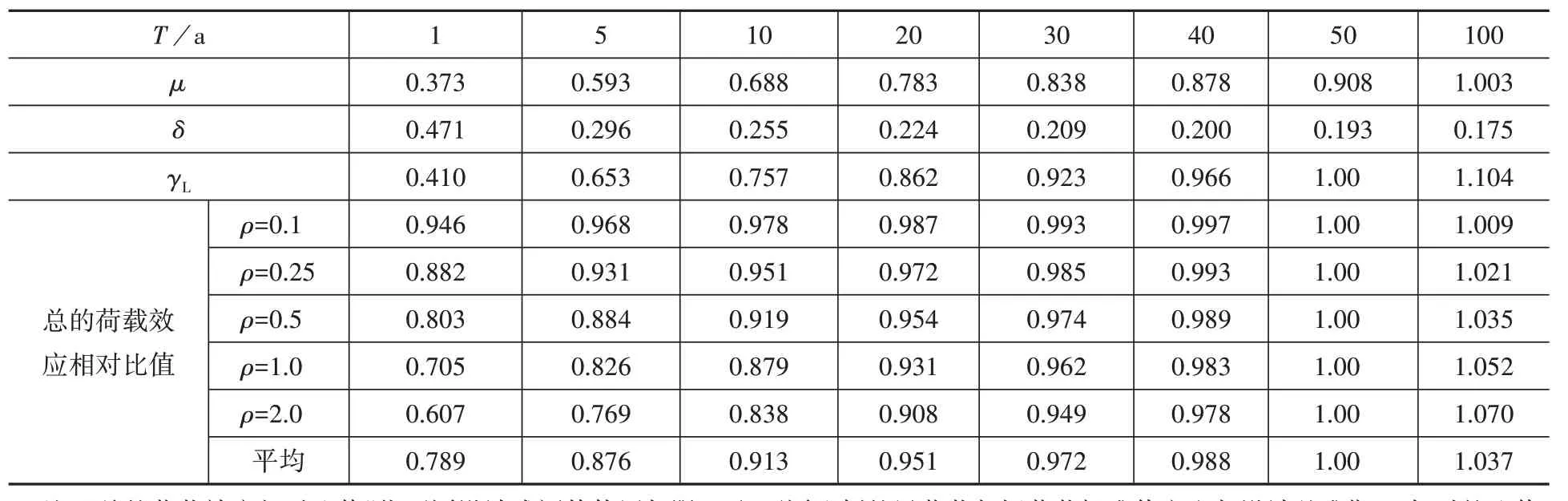
表2 风荷载QT的统计参数Table 2 Statistical parameters of wind load QT
综合上述分析,当不考虑抗力退化时,可认为结构的累积失效概率与服役年数成正比。因此,当设计使用年限缩短时,可对累积失效概率进行线性折减确定抗力需求折减系数,代替现行规范[15]和文献[16-17]中的可变荷载标准值折减。显然,采用抗力需求折减的方式可建立结构可靠指标(或累积失效概率)与使用年限之间更明确、更直接的关系。
2 抗力退化时不同时段的累积失效概率和可靠指标分析
2.1 基本分析方法
考虑抗力退化时,式(1)变为

式中,R(t)为时变抗力随机过程,多数文献将R(t)简化为如下的随机过程模型[8-11]:

其中,R0为服役期起始点的抗力随机变量,φ(t)为抗力衰减函数,是一个确定性函数。
当荷载效应保持不变时,抗力退化结构在短时段内的失效概率必然有前小后大的趋势,当对评估使用年限内的累积失效概率进行近似计算时,可用评估使用年限内的抗力平均值作为随机变量,代替抗力随机过程,式(2)进一步简化为


对于既有结构评定,

其中,T0为新建结构的设计使用年限,t0为既有结构评定时的服役年数,T′为既有结构的评估使用年限。
2.2 累积失效概率和可靠指标的发展规律
为考察抗力退化对不同使用年限内结构的累积失效概率和可靠指标的影响,仍用第1 节中钢筋混凝土梁的受弯承载力为例进行分析。取ρ=2.0,抗力衰减函数用如下的二次函数表达:

当参数α=0 时,代表结构抗力不退化。当参数α取 0.000 02、0.000 04、0.000 08 时,分别代表结构抗力轻度退化、中等退化和严重退化三种情况。由式(7)可得,服役50 年后结构的抗力退化率φ(50)分别为0.95、0.9 和0.8,其相应的φ(100)分别为0.8、0.6和0.2。用JC法计算在上述四种情况下的构件可靠指标β′(T),并将其换算为累积失效概率Pf(T),结果见图2、图3。这里用β′(T)区别于文献[13]中不考虑抗力退化的可靠指标β(T)。
图2 为不同服役年数下的结构累积失效概率Pf(T)-T曲线。可以看出,抗力不退化时的累积失效概率与服役年数成正比。抗力退化时,Pf(T)-T曲线为抛物线,相对于抗力不退化的情况,前30年内Pf(T)-T曲线差别不大,但服役超过30后,四种情况下的Pf(T)-T曲线的分化迅速增大。抗力退化程度越严重,Pf(T)-T曲线增长越快;如T=60 a 时的累积失效概率与T=50 a 时相比,抗力不退化时只增大0.000 1 左右,而抗力严重退化时增大了0.001 4左右,即后者为前者的14倍左右。
图3 为不同服役年数下的可靠指标β′(T)-T曲线,该曲线与图2的Pf(T)-T曲线对应。可以看出,抗力不退化时,服役前10 年内的可靠指标迅速减小,而后减小速率趋缓;当抗力退化时,服役前 30 年内的β′(T)-T曲线的差别不大,如T=30 a时的可靠指标,抗力不退化时为3.404,抗力轻度退化、中等退化和严重退化时分别为3.379、3.352、3.300,四者的比值为1∶0.99∶0.98∶0.97。服役超过30年后曲线的分化明显增大,如T=50 a时的可靠指标,抗力不退化时为3.264,抗力轻度退化、中等退化和严重退化时分别为3.178、3.114、2.952,四者的比值为1:0.97:0.95:0.90;若以目标可靠指标为[β]-0.25=2.95 为标准,此时各种情况下的安全性仍满足要求。T=100 a时的可靠指标,抗力不退化时为3.064,抗力轻度退化、中等退化和严重退化时分别为2.735、2.375、1.488,四者的比值变为1∶0.89∶0.78∶0.49;抗力不退化时的可靠指标仍大于2.95,抗力轻度退化时的可靠指标低于2.95但仍大于安全等级为三级的目标可靠指标2.7,而抗力中等退化和严重退化时的可靠指标严重不足。

图2 不同抗力退化程度下的累积失效概率发展规律Fig.2 Development law for cumulative failure probability under different degree resistance degradation

图3 不同抗力退化程度下的可靠指标发展规律Fig.3 Development law for reliability index under different degree resistance degradation
2.3 等时段内结构失效概率和可靠指标的变化
图4和图5分别为等时段(以每10年为一个时段)内结构失效概率和可靠指标的变化过程。可见,抗力不退化结构在等时段内的失效概率和可靠指标曲线是一条水平直线;抗力退化时,结构失效概率和可靠指标的差异迅速扩大。抗力不退化结构在10年时段内的失效概率保持为0.000 11,当服役期末的时点t=30 a 时,四种不同抗力退化程度下的10年时段失效概率之比为1∶1.5∶2.3∶5,而当t=50 a 时,该比值扩大至1∶2.7∶7.1∶46.8。相应地,抗力不退化结构在10 年时段内的可靠指标保持为3.686,当t=30 a 时,四种不同抗力退化程度下的 10 年时段可靠指标之比为 1∶0.97∶0.95∶0.89,而 当t=50 a 时 ,该 比 值 扩 大 至 1∶0.93∶0.86∶0.69。

图4 10年时段内的失效概率变化规律Fig.4 Development law for failure probability within a 10-year period

图5 10年时段内的可靠指标变化规律Fig.5 Development law for reliability index within a 10-year period
2.4 设计和评估使用年限内的可靠度与分段可靠度的关系
从理论上分析,如果各随机变量保持不变或在各时段内相互统计独立,则某一设计或评估使用年限内的可靠度可通过对应各分段可靠度的乘积计算得到。那么,当抗力按式(3)所示规律退化时,是否仍有这种规律?对于上述实例,通过分段(T=10 a)失效概率得到分段可靠度,再将对应于各设计或评估使用年限的各分段可靠度相乘得到累积可靠度,然后将其换算为可靠指标,与直接计算的设计或评估使用年限内的可靠指标相比较,结果见表3。
由表3 可见,抗力不退化时,分段换算的可靠指标略小于直接计算值,两者相差不超过0.3%。抗力不很严重时(轻度退化全过程,中等退化时的前50年,或严重退化时的前30年内),两者相差一般不超过1%。抗力退化严重时(中等退化或严重退化时的其他时段内),两者的差别迅速增大,多数时段内仍不大于5%,而严重退化时自t=50 a 开始的30 年内,差别增大至35%。总体而言,对于抗力退化不很严重的时段,两种算法十分接近;而对于抗力退化很严重的时段,两种算法相差较大。误差增大的原因,是分段换算方法实质上假定了抗力在各时段内完全独立,而直接计算方法实质上假定了抗力在各时段内完全相关。实际抗力退化结构在各时段内的相关性介于完全独立与完全相关之间,两个不同时段在时间上越接近其抗力退化相关性越大[12]。因此,当抗力退化很严重时,实际结构的可靠指标介于直接计算方法与分段换算方法之间。
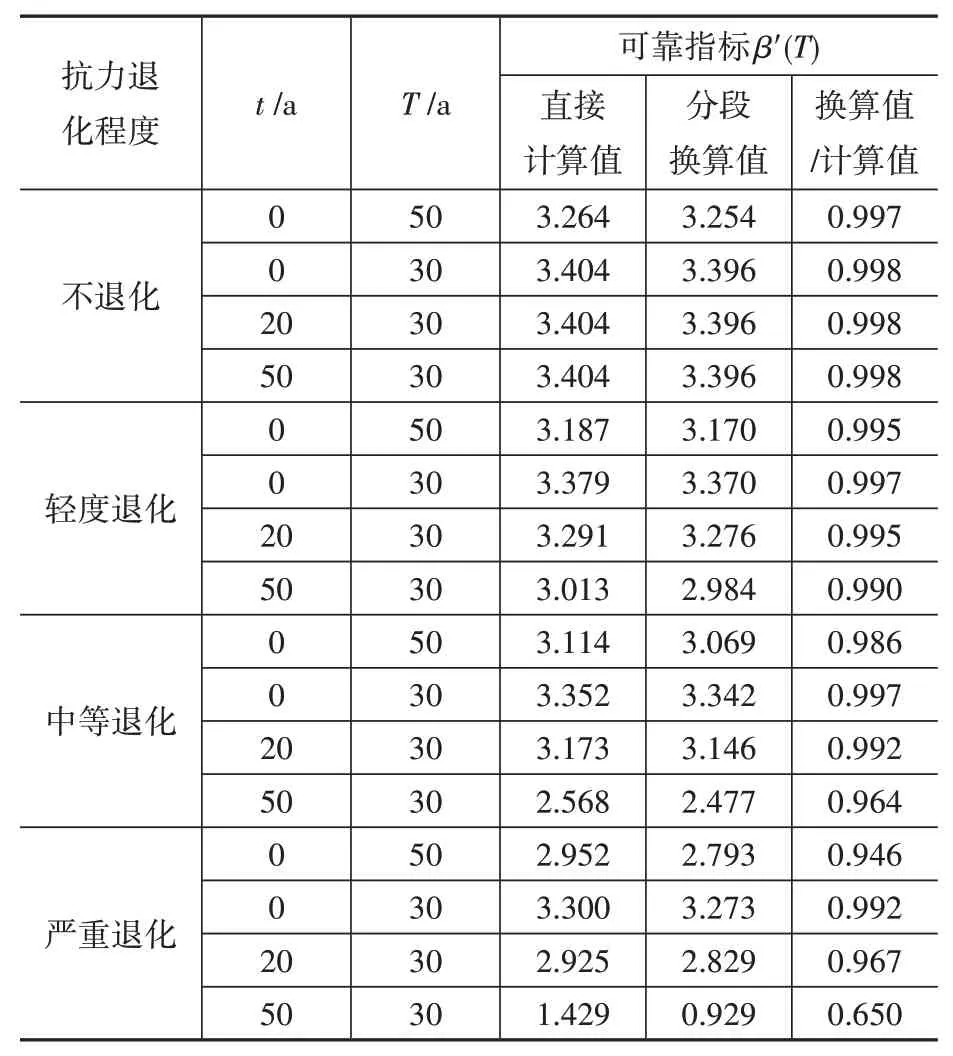
表3 不同使用年限内直接计算与分段换算的可靠指标比较Table 3 Comparison of reliability indexes calculated by direct calculation and segmental conversion
3 折减系数法与可靠度法计算结果的比较
根据文献[13],假定抗力R和荷载效应S均为正态分布,且设计或评估使用年限缩短为T时,荷载效应的平均值减小为μs(T)而标准差保持不变时,荷载效应折减系数λs(T)可近似按下式计算:

进一步假定抗力退化时,抗力平均值减小而标准差保持不变,则有

式中,φ*为评估使用年限T内的平均抗力退化系数。
当K0、φ*和λs(T)三个参数已知时,可根据式(9)近似计算β′(T)/β0。将计算得到的β′(T)/β0与根据可靠度法直接计算(即JC 法)得到的β′(T)/β0进行比较,可以间接对比上述近似算法与可靠度法的计算结果。
表4 列出本文实例中不同时段内近似算法与可靠度法计算的β′(T)/β0比较。近似算法与可靠度法计算值的比值在0.86~1.01之间;抗力退化越严重,两种方法之间的误差越大。分析两者计算结果的误差,主要来自以下两个方面:
(1)按可靠度法直接计算β′(T)/β0时,由于抗力随机过程采用式(3)所示模型,抗力标准差与平均值同步减小,故变异系数保持不变。但根据钢筋锈蚀引起的抗力退化研究成果[6-7,12],随着耐久性劣化的发展,抗力平均值减小时,标准差反而增大,变异系数也增大。故可靠度法计算结果略偏于不安全。
(2)根据文献[13],按近似算法计算β′(T)/β0时,采用了三个假定:抗力和荷载效应随机变量均为正态分布,荷载效应随机变量的标准差不变,抗力标准差也不变。这三个假定均有近似性,抗力退化严重或使用年限明显缩短时,近似法的误差会增大。本文实例的计算结果中已反映出这个规律。
总体上,近似算法能反映抗力退化与使用年限缩短引起的结构时变可靠度变化规律,便于工程应用。
4 结 论
本文考虑服役期内的抗力退化和评估使用年限缩短,对钢筋混凝土梁受弯承载力进行时变可靠度分析,得到如下结论:

表4 近似法与可靠度法(JC法)计算的β′(T)/β0比较Table 4Comparison of β′(T)/β0between approximate method and JC method
(1)不考虑抗力退化时,总体上存在“累积失效概率与服役年数成正比”的规律。
(2)以二次曲线近似表达混凝土梁受弯承载力的退化过程,比较了不同抗力退化率下结构累积失效概率及可靠指标的发展规律。
(3)分析了等时段内结构失效概率及其对应可靠指标的变化,发现有如下规律:抗力退化不很严重时,分段可靠度的乘积接近设计或评估使用年限内的可靠度,但抗力退化严重时,这个规律不存在。
(4)通过算例与可靠度法比较分析表明,采用抗力退化系数-荷载效应折减系数近似计算的方法总体上能反映抗力退化与使用年限缩短引起的结构时变可靠度变化规律,便于工程应用。
