一日内与逐日的双动态网络交通流演化
2020-08-26陈文思
陈文思
(福建省城乡规划设计研究院 福州 350116)
0 引 言
出行者的出发时间与路径选择行为是影响网络交通流变化的重要因素,要解决城市交通拥堵问题除了探索出行者的路径选择行为,还必须考虑出行者的出发时间选择行为对网络交通流的影响,建立相应的模型来刻画交通流的时空分布.
综合考虑出发时间与路径选择的网络交通流研究分为两类:①假设平衡存在,以网络交通流的平衡态为对象,进行同时考虑出发时间与路径选择的动态交通分配研究[1];②研究探讨平衡是否存在的问题,平衡态不是它的研究重点,它更多关注的是网络交通流的动态演化过程.从Horowitz[2]最早基于包含两条路径的简单网络进行交通流演化研究开始,针对出行者单一出行选择行为下的网络交通流演化研究成果颇丰[3],而综合考虑出发时间与路径选择的网络交通流演化研究也受到学者们的关注.Mahmassani等[4]先在单一路径下,通过一系列仿真实验方法,研究城市通勤出行者的逐日出发时间选择的动态特性,随后,又进一步引入路径选择行为,对城市通勤者的路径与出发时间选择动态特性进行实验研究,该研究侧重各路径出发时间分布的变化情况以及出发时间与路径调整次数的统计分析,未分析流量演化规律.Cascetta等[5]基于历史出行时间与费用信息,建立了1 d内与逐日(day-to-day and within-day)的双动态模型,但该研究侧重分析网络流量在1 d内的变化,对于各时段网络流量逐日演化规律未做深入分析.Ziliaskopoulos等[6]针对同时考虑出行者出发时间与路径选择的情况下,通过建立仿真模型研究网络交通流演化,该研究分析了网络交通流达到均衡的条件,但对于网络交通流演化不稳定情况缺乏分析.陈玲娟等[7]研究出行者逐日出发时间及路径选择的变化规律,得出考虑出发时刻选择的路网流量波动较大,但未进一步分析参数对交通网络波动规律的影响.刘诗序等[8]在考虑出行者的出发时间选择行为影响下,分析网络交通流演化规律,但逐日的路网流量未考虑多时段的情形.
针对以往研究中存在的问题,本文根据出行者的出发时间与路径选择过程,针对一般交通网络建立1 d内与逐日的双动态模型,在考虑出行费用的构成中,除了包括由行程时间转化的费用外,还考虑由到达时间产生的早到/迟到附加费用.通过数值实验,对各时段各路径流量逐日演化规律做进一步分析.
1 一日内与逐日网络交通流更新规则
综合考虑1 d内与逐日的双动态网络交通流演化过程,见图1.本研究的时段假设为高峰时段,出发时段的交通需求量假设是固定的.
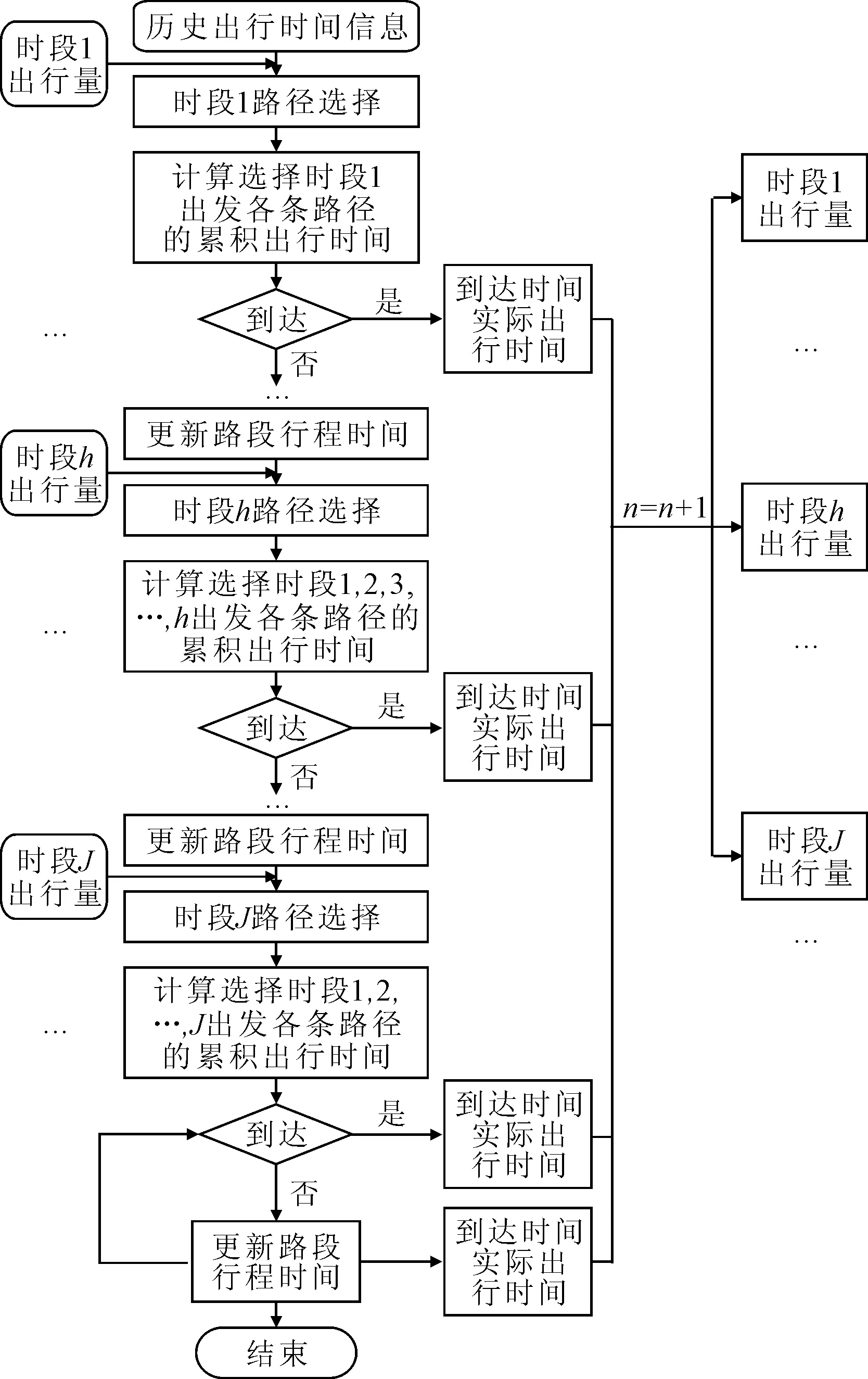
图1 1 d内与逐日的双动态网络交通流演化过程
2 一日内与逐日的双动态网络交通流演化模型
2.1 出发时段交通需求量逐日更新模型

(1)
式中:φ为权重系数,且0≤φ≤1.φ的大小反映了出行者对前1 d出行感知效用的依赖程度,φ越大,依赖程度越大,反之,φ越小,依赖程度越小.
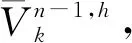
(2)

(3)
则,第n天选择时段h出发的概率:
(4)
式中:Vh反映出行者在其他条件一致的情况下,对时段h选择的偏好效用.
第n天选择时段h出发的交通需求量为
qn,h=DPn,h
(5)
2.2 一日内路径选择模型
确定了出行的出发时间后,当天的出发时间不再变动.而当天出发前的路网信息,仍会影响出行者的路径选择.假设第n天选择时段h路径k出行的出行者在时段t结束时的累积出行时间:
(6)
第n天在时段t时,路段a的交通量为
(7)
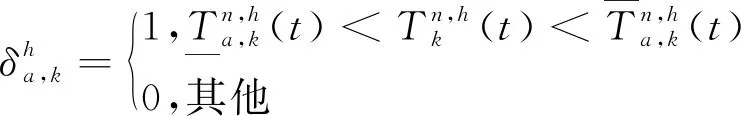
(8)
(9)
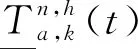
针对在不同出发时段下选择的各条路径所包含路段的行程时间更新分为以下三种情况.
1) 当前位置对应的路段行程时间更新 确定了选择各时段各路径出行的交通量在路网上的当前位置后,针对选择不同出发时间和不同路径出行的交通量,沿着选择的路径行驶,到达相应路段后,需对选择该出发时间出行,相应路段的行程时间进行更新,分成已走过的路段和剩余未走过的路段两部分.则第n天选择时段h路径k出行的交通量,沿路径k行驶,在时段t时到达路段a,则该路径包含的路段a的行程时间更新(见图2):
(10)
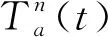

图2 路径包含的路段行程时间更新示意图
2) 当前位置之前的路段行程时间更新 在路段a之前的路段,也就是选择时段h路径k出行的交通量在时段t时已经走过的路段,这些路段的行程时间保持不变:
(11)
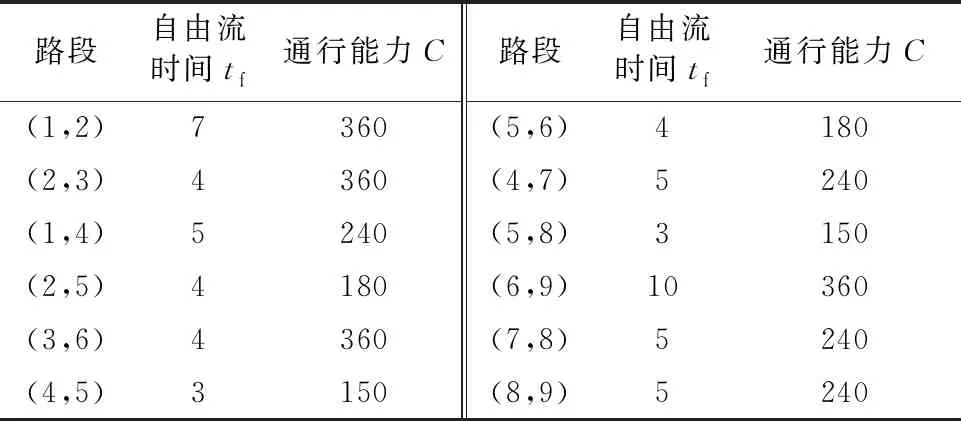
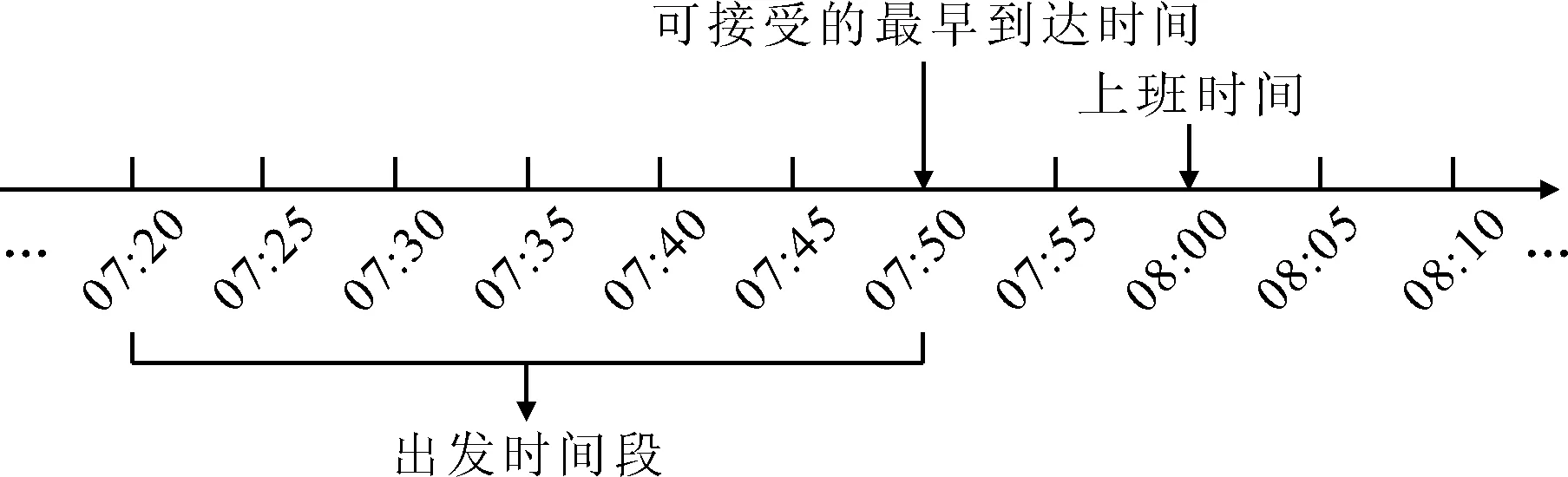
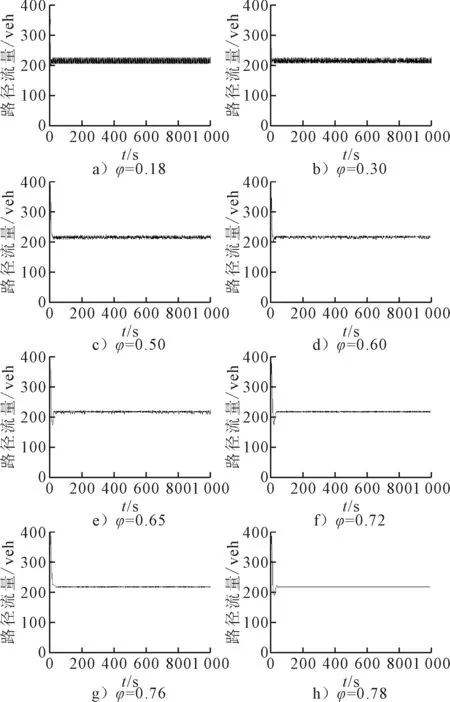
其中,i 3) 当前位置之后的路段行程时间更新 在路段a之后的路段,也就是选择时段h路径k出行的交通量在时段t时即将通过或者还未通过的路段,该部分路段的行程时间: (12) 其中:i>a. 假设各路段行程时间仅与路段交通量相关,第n天时段t路段a的行程时间函数为 (13) 第n天时段t路径k的行程时间: (14) 第n天下一时段(t+1)选择路径k的概率: (15) (16) 则第n天时段t+1选择路径k的交通量: (17) (18) 图3为路网示意图,实验路网包含一个OD对,其中节点1为起点,节点9为讫点.路网共有9个节点,12条路段,每个路段的行程时间t关于该路段交通量q的函数为t=tf[1+0.15(q/C)4],其中tf为路段自由流行程时间,C为路段通行能力,各路段的tf与C的取值见表1. 图3 路网示意图 表1 参数取值 本次实验模拟的总时长为100 min,研究时间范围为07:20—09:00,划分的时间间隔为5 min,共划分为20个时段.其中,出行者的出发时间范围为07:20—07:50,共六个时段,另外,出行者可接受的最早达到时间为07:50,上班时间为08:00,具体时段划分情况见图4.可选择的出发时段的OD需求量为2 400 veh,其他时段为平峰时段,各平峰时段的OD需求量假设为100 veh,出行者共有6条路径可供选择,实验天数为1 000 d.参数取值θ1=1;θ2=1;θ3=3. 图4 研究时段划分情况 本文在参数φ与λ取不同值的条件下进行仿真实验,考察各时段各路径交通流演化情况.其中参数φ反映了出行者对前一天出行感知效用的依赖程度,参数λ反映出行者在时段选择时对时段感知效用的敏感程度.通过设定参数λ和φ的不同值,进行大量数值实验,发现各时段各路径的演化规律均类似.下面固定λ=0.90,选取φ=0.18,0.30,0.50,0.60,0.65,0.72,0.76,0.78的条件下,以时段2路径1-4-5-8-9的仿真结果为例进行分析,见图5. 图5 λ= 0.90时φ取不同值时时段2路径1-4-5-8-9上的流量动态演化 由图5可知,选择时段2下的路径1-4-5-8-9出行的流量演化规律:φ取值较小时,选择时段2下的路径1-4-5-8-9出行的流量随着天数的波动较大,随着φ值的增大,该时段下对应路径流量的波动也越来越小,当φ超过一定值时,系统随着天数的演化最终会达到平衡状态. 通过固定λ值,对不同φ值下各时段各路径的流量演化规律进行初步探讨,得到随着φ值增大,各时段各路径流量随天数演化出现的波动越来越小,当φ值增大到一定值时,系统随天数演化会达到稳定状态. 通过数值实验,绘制出系统关于参数φ和λ的状态划分图,见图6.从横向来看,随φ值增大,系统演化状态最终均为稳定状态,但是随φ值变化过程中,不再呈现波动逐渐减小最后达到稳定的统一规律,并且还发现当λ很小时,不论φ取何值,系统均稳定.从纵向来看,当φ≤0.82时,系统随λ值增大,系统演化状态最终均为不稳定状态.相反,当φ>0.82时,系统随λ值增大,系统演化状态最终均为稳定状态.在随λ值变化过程中,均表现出稳定与波动交替出现的规律. 图6 系统关于φ和λ的状态划分图 1) 固定参数λ时,随着参数φ增大,各时段网络交通流演化最终会达到平衡状态;而参数λ对各时段网络交通流演化规律的影响较为复杂,当参数φ≤0.82时,随着参数λ变化,各时段网络交通流随着天数演化结果最终均为波动状态,反之,最终均为稳定状态. 2) 参数λ反映出行者在时段选择时对时段感知费用的敏感程度,λ越大时,反映出行者对时段感知费用越敏感,参数φ反映了出行者对前1 d出行感知效用的依赖程度,φ越小时,意味着出行者对前1 d出行感知效用的依赖程度越小,出行者越倾向于根据实际路网信息选择相应时段和路径出行.当参数λ较大而参数φ较小时,意味着对时段感知费用敏感的出行群体,根据实际路网信息选择相应时段和路径出行,更容易使网络达到稳定状态.相反,当参数λ和参数φ均较大时,意味着对时段感知费用敏感的出行群体,根据路径出行感知效用选择相应时段和路径出行,反而会使网络处于波动状态.因此,出行者在进行时段与路径选择时,出行者对出行感知效用的依赖程度以及对时段感知费用的敏感性均显著影响网络交通演化结果.
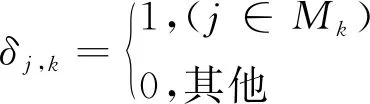
3 模拟实验设计

4 系统演化规律

5 结 论
