基于离散元的拔桩过程中土体动力响应分析*

孙亭亭 杨吉新* 张志华 杨竟南 张 璇 石 旷

(武汉理工大学交通学院1) 武汉 430063) (长江水利委员会长江科学院2) 武汉 430010)

0 引 言

在桥梁建设中，经常需要借助钢管桩作为临时支撑体系来承担各种施工荷载，在施工完成后会把临时支撑体系拆除，这就涉及到拔桩的相关问题，特别是对于入土较深的钢管桩.

目前学者对抗拔桩的研究比较多，陈昌富等[1]通过建立桩-土传递模型，分析了抗拔桩在不同荷载下的桩体位移.刘梅等[2]研究了不同桩长的抗拔桩在不同地基中的破坏模式.Moayedi等[3]采用模拟器模拟了地震荷载的作用，研究了在地震作用下土层的剪切波速度的变化情况.闫澍旺等[4]运用自制直剪仪，结合土体参数提出了“抗剪糙度”的概念，并分析了其变化规律的影响.史吏等[5]对群桩基础的动力特性进行分析，得出荷载频率越高，地基位移衰减越快的结论.

上述研究主要通过试验的方法对桩-土进行研究，在数值仿真方面，出现了有限差分法(FDM)、边界元法(BEM)，以及离散元法(DEM)等数值计算方法，相对来说离散元在解决岩土工程时有特殊的优势.Zhan等[6]以颗粒流理论为基础，利用PFC2D研究了土体堵塞的形成规律.周喻等[7]基于颗粒流理论，研究了荷载-桩体位移关系、土体变形及地基位移场分布.袁贵涛[8]采用颗粒离散元的方法，分析了在高频反复剪切荷载作用下振动参数对土体参数的影响.Fattah等[9]讨论了土塞效应对钢管桩极限承载力的影响.Zhang等[10-12]采用2D DEM模型进行了土体剪切振动分析，通过振动直剪，对剪切力，孔隙率，体积应变和配位数等进行研究.可以看出，离散元既能模拟土体颗粒的宏观力学状态，又能分析细观变化，具有其他方法所不能比拟的优点[13].但是上述学者对拔桩过程中土体参数响应的研究比较少，不能满足拔桩时桩-土参数计算的需要，同时，受到现场环境限制施工中较难测试拔桩过程中的土体参数.基于此，本文利用PFC2D软件，建立拔桩数值模型，从颗粒变化的细观角度研究了不同振动频率下颗粒响应状态，分析了拔桩时颗粒的运动规律，监测了拔桩敏感区域土体参数响应情况.

1 桩-土理论和离散元理论

1.1 桩-土理论

按照Winkler模型，桩土相互作用可以用阻尼和缓冲器系统来进行模拟，见图1.桩-土的波动方程[14]为

(1)

式中：Pz为土层每米中的能量；Cz为阻尼系数；Kz为刚度系数；ω为振动频率；r为桩的半径；t为时间.

图1 桩土之间效应

1.2 离散元理论

离散元是Cundall在19世纪70年代提出的，计算时利用牛顿第二定律和力-位移定律对颗粒进行迭代计算，颗粒之间的接触力和颗粒的体力确定颗粒运动和更新颗粒的速度和位置关系，接触力在接触面上分为法向量和切向量[15].为了详细研究颗粒之间的相互作用力，本文引入线性接触黏结模型，颗粒之间的接触状态见图2.

图2 颗粒之间的接触状态

控制方程为

(2)

(3)

式中：mi为颗粒i的质量；Ii为颗粒i的转动惯量；ui为颗粒i的平动速度；ωi为颗粒i的转动速度.颗粒所受的力和力矩主要有：重力mig，颗粒i与颗粒j的法向接触力Fcn,ij和切向接触力Fct,ij，法向阻尼力Fdn,ij和切向阻尼力Fdt,ij.图2中Tij为切向和力矩，可以分解成切向转矩Tt,ij和摩擦转矩Tr,ij，其中Tt,ij为由切向力产生引起颗粒i发生转动的力矩，Tr,ij是阻止颗粒i发生转动的力矩.

2 工程概况和建模介绍

2.1 工程概况

建宁大桥新建工程位于湖北省石首市，桥梁总长548 m，主桥主梁断面全宽45.8 m，桥梁横断面宽35.5～41.5 m.地质条件如下：山底湖水深1～2 m，无流速，在勘探所达深度范围内，从表层往下地质依次为灰黑色黏土、黄色黏土、黄色粉土、青灰色粉土、青灰色粉沙，层厚1.8～24 m.其中入土深度最长为26 m，水深2 m.桩土分布情况见图3.

图3 桩土分布示意图

2.2 数值模型

首先建立墙体(wall)来模拟土体的边界，建立了40 m×50 m的区域.土体颗粒细观参数取值参考文献[16]中进行取值.土体颗粒采用线性接触黏结模型，在模型控制范围内随机生成颗粒，颗粒按随机方式在给定的范围内排列.结合文献中试验数据和地质报告中的相关参数.本文不考虑水渗透的影响，鉴于待拔桩的入土深度，土体均采用黄色黏土.

采用颗粒簇(clump)建立待拔桩，桩体参数参考文献[17]中进行取值，不考虑拔桩时桩体的受力变化，假设待拔桩为刚体.模型建模取值见表1.待拔桩直径1 m、长度28 m(其中地下埋深26 m，露出地面2 m).模型共构建了68 051个ball球体单元，2 701个clump桩体单元.结合实际的工程特点，分别选择了在拔桩过程中有重要影响的5个监测区域布置监控测量圆，测量圆直径1 m.颗粒和测量圆布置图见图4.

2.3 桩体振动曲线

在拔桩时利用振动设备进行加载，主要施加不同的振动频率，示意图中选取30 Hz振动频率进行加载到桩顶，见图5.

表1 模型参数取值

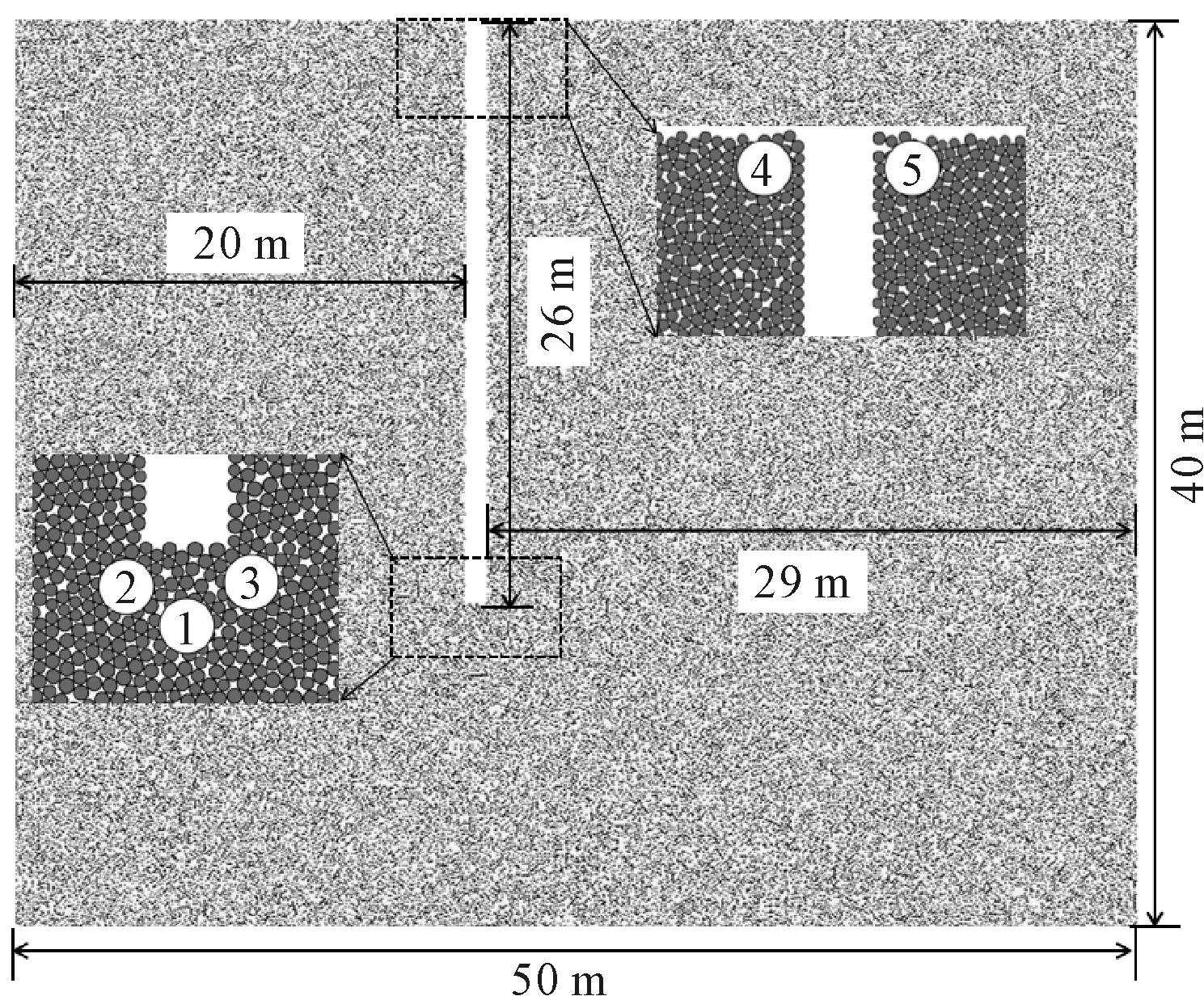
图4 颗粒模型图

图5 桩顶振动加载曲线

3 拔桩响应分析

3.1 颗粒位移变化分析

选择在四种振动频率下的x方向颗粒变化情况绘制位移云图进行分析，选取颗粒位移变化比较明显的水平区域[16,25] m和竖直区域[13,20] m范围.提取位移变化0.5 m以上的颗粒绘图，见图6.由图6可知，桩基底部在振动荷载的作用下1号测点区域颗粒变化不大，2和3号测点区域土颗粒变化现象明显，2号土体测点区域颗粒向上运动，3号测点土体颗粒向下运动.在图6c)中颗粒位移范围逐渐扩大，图6d)中桩底部颗粒出现散开幅度较大，主要是因为在频率荷载作用下土体随荷载变化明显，并出现填充拔桩空隙的趋势.

图6 不同振动频率下的x方向土颗粒位移云图

为了详细研究不同振动频率下土体颗粒的变化情况，对10，20，30，40和50 Hz这五种频率作用下的y方向的颗粒运动进行分析，提取2号测点区域和3号测点区域计算数据，绘制时间-位移曲线图，见图7、图8.

图7 2号测点位移图

图8 3号测点位移图

由图7可知，位移变化跌宕起伏比较复杂，最终整体呈现上升趋势.在初始阶段0～0.09 h内所有位移变化均呈现线性增长的趋势；0.09～0.19 h内，五种振动频率下的位移变化也是呈现上升趋势，且以50 Hz作用下上升幅度最大，在0.17 h时刻达到这个区域峰值15.90 mm，在这个时间段内的变化趋势和文献[18]一致；在0.35～0.45 h内，土体颗粒位移随振动频率大小变化不明显，大频率作用下位移反而较小，主要是因为土体在振动后慢慢出现重组的现象，土体间的相互作用力发生变化，接触面也随着改变，位移基本稳定在15 mm左右；在后面的时间中，颗粒位移不断增加，最大值出现在50 Hz时，达到67 mm左右.在0.5 h后位移和频率之间变化基本一致，各种振动频率之间都是呈现上升趋势，且50 Hz增长变化幅度最大.

在图6的云图中，土体颗粒上升和下降有明显的分界线，分界线处土体基本没有位移变化.由图8可知，在0～0.12 h内，土体在不同振动频率的作用下出现上下波动的情况，在0.1 h时波动达到最大值2 mm左右，而后位移逐渐减小，最小位移出现在10 Hz时数值是-0.3 mm，变化趋势和文献[18]一致；在0.25～0.4 h内20 Hz作用下土体主要发生向下的位移，值为-8 mm，在40和50 Hz作用下颗粒发生向上位移明显，在50 Hz作用下颗粒运动达到最大值12 mm，在高频振动作用下颗粒散开并向上运动，低频振动荷载作用下向下运动，说明在低频作用下颗粒发生聚集的现象；在0.5 h后的曲线图中可以看出，土体位移和频率变化呈现一定的规律性，频率越大位移越大，这说明在振动荷载的作用下，一段时间后土体伴随振动产生运动，颗粒不断产生分散和重组的情况.在50 Hz作用下颗粒位移重组现象明显，说明在待拔桩拔起时颗粒往下填充了拔桩空隙.本文中计算结果呈现的规律性和文献[15]中试验得出的结果基本一致，验证了本文计算方法的可行性和参数选取的准确性.

3.2 颗粒速度变化分析

在位移分析中主要是y方向的位移变化幅度比较大，本节主要分析在20，30，40和50 Hz不同振动频率下桩周土体颗粒速度分布，本文选择速度在5 m/s以上的颗粒分布做云图，为了更准确体现颗粒变化情况，选择水平区域[16,25] m和竖直区域[13,20] m，见图9.

图9 不同振动频率下的桩底土颗粒速度云图

由图9可知，振动频率对颗粒的运动速度有较大的影响，20 Hz作用下颗粒速度在5 m/s以上的分布较少，30，40和50 Hz作用下颗粒分布明显增加.主要体现在桩基底部颗粒运动速度较大，因为在拔桩过程中下部颗粒发生向上或者向下的位移明显，向上运动伴随着拔桩同时产生，向下运动填充了拔桩的空隙，同时拔桩过程中带动桩基底部颗粒向上运动，桩侧颗粒分布范围比较大.

3.3 颗粒受力变化分析

相对于连续性材料，土体颗粒作用离散的单体颗粒，颗粒之间会因为外界荷载的作用发生相对的位移变化、速度变化和受力变化，但是他们之间的传递不是连续的，是通过颗粒之间的连接作用进行传递的.由颗粒连接理论可以看出颗粒之间相互作用使得颗粒受力情况比较复杂.本文主要考虑拔桩5 m高处时，20，30，40和50 Hz四种振动频率下的颗粒受力变化情况，本节主要考虑拔桩时受力影响较大的2号测点区域和5号测点区域.

从前文所述可以看出2号测点区域位移变化和速度变化均比较复杂，现选择2号区域进行颗粒受力状态分析.绘制力-时间曲线图，见图10.在振动荷载作用下颗粒受力情况和振动情况相似呈现上下波动情况，尤其是低频作用下更加明显；由图10a)可知，前期阶段土颗粒受力较小，在0.5 h之内受力波动逐渐增大，达到最大的峰值，最大值182.87 kN和最小值-155.46 kN，随后波峰和波谷呈现逐渐减小的趋势，经过反复震荡后，最后回归为零；图10b)和c)也呈现相应的规律，出现反复震荡的情况，只不过波峰波谷出现的时间更晚；图10d)中达到整个拔桩过程中波峰波谷的最值，最大值238.16 kN和最小值-306.72 kN，前期颗粒受力波动较大，后期逐渐平缓.对于图10中各不同振动频率下呈现的规律，可以看出整体图形中颗粒伴随着振动的持续不断变化，受力和加载曲线基本一致，图中受力为零的位置说明在振动中颗粒出现不断的重组和分散.

图10 拔桩5 m高度时2号测点各频率作用下颗粒受力图

对5号测点绘制在20 Hz、30 Hz、40 Hz和50 Hz四种振动频率下的颗粒受力曲线图，选择对颗粒受力影响比较大的前1 h进行分析，见图11.从总的图形分布中可知，颗粒受力状态都是从0点开始，刚开始围绕0点上下波动，波动频率和2号测点区域类似，但是总体上下波动幅度不大，前期都是呈现上升的趋势.经过一段时间的重组后，土颗粒出现相互挤压和重组的情况，使得土颗粒的受力发生变化，随着集聚的不断增加，达到一个极值最后下落，然后出现各图中所示的波峰和波谷.由图11a)可知，颗粒受力最大值116.31 kN和最小值-37.10 kN；由图11b)可知，颗粒受力最大值115.26 kN和最小值-30.36 kN；由图11c)可知，颗粒受力最大值113.26 kN和最小值-28.54 kN；由图11d)可知，颗粒受力最大值105.32 kN和最小值-35.17 kN.前期波动明显，但是都在-50～50 kN振荡，说明颗粒重组和散开现象明显和前文中位移和速度变化规律一致.

图11 拔桩5 m高度时5号测点各频率作用下颗粒受力图

4 结 论

1) 选择水平区域[16,25] m和竖直区域[13,20] m的颗粒，分析x方向和y方向的位移变化.2号测点y方向5种振动频率下从位移变化也是呈现上升趋势，且以50 Hz作用下上升幅度最大，达到区域峰值15.90 mm；3号测点在0.1 h波动位移达到最大值2 mm，而后位移逐渐减小，最小位移出现在10 Hz时数值是-0.3 mm，本文中计算结果呈现的规律性和文献[18]中试验得出的结果基本一致，验证了本文计算方法的可行性和参数选取的准确性.

2) 从选定区域内的颗粒运动速度来看，颗粒运动速度较大的位置主要集中在桩侧和桩底，桩侧速度分布沿着横向坐标依次递减，说明拔桩过程中对桩侧土体影响比较大，颗粒之间相互传递效应明显.位移分布也是呈现这一特点，速度变化趋势和位移变化趋势基本一致.

3) 对于颗粒受力变化，主要考虑拔桩时受力影响较大的2号测点区域和5号测点区域.对于2号测点在50 Hz作用下颗粒受力差值最大，主要在最小值-306.72 kN和最大值238.16 kN之间跳动，对于5号测点最大值116.31 kN和最小值-37.10 kN，从数值变化中说明颗粒不断进行分散和重组，颗粒受力变化与位移变化和速度变化呈现相同的规律性.