基于航海雷达的船舶自动定位方法研究*

吴建华 戴卓鑫 王 政 俞飞飞 吴小红

(武汉理工大学航运学院1) 武汉 430063) (内河航运技术湖北省重点实验室2) 武汉 430063)

0 引 言

在极地航行过程中，精准可靠的船舶定位与导航是保障船舶航行安全的主要措施[1-3]，同时也是降低船舶运营成本的重要手段[4].随着电子信息技术的发展，无线电定位技术在船舶定位与导航中占据了主导地位，其中，以GPS定位为代表的卫星导航定位技术以其精度高、覆盖范围广、使用方便等特点，成为目前船舶定位的首选[5-8].但是，卫星导航定位技术依赖于接收外界的卫星信号，在极地区域极端条件下，可能会影响其使用的可靠性[9-10]，需要一种应急定位方法.近岸航行时，尤其是在沿岸10 n mile之内，雷达能够提供较高船舶定位精度，是驾驶员备选的定位设备，在卫星定位设备出现异常时可提供船舶定位[11-12].

传统的雷达定位是通过驾驶员对比海图与雷达图像，选择合适的定位目标，测量目标的距离或方位，在海图上画出定位目标到本船的距离、方位位置线，两个或多个位置线交点即为本船船位.针对人工雷达定位操作繁琐、定位误差大、难以提供连续定位的局限性，本研究基于参考物标的位置信息，利用雷达的目标跟踪功能，自动获取参考目标到本船的距离、方位数据，借助航迹推算数学模型推算出本船的船位经纬度数据，从而实现雷达自动定位功能，为沿岸航行船舶提供一种快速、连续、准确的雷达定位方法.

1 船位推算数学模型

已知某参考物标A的经纬度为(λA,φA)，在雷达上测得物标A相对本船的真方位为θ，距离为R，为了推算出本船O处的经纬度数据，将物标距离R沿经线、纬线分解为SY=Rcosθ，SX=Rsinθ，见图1.

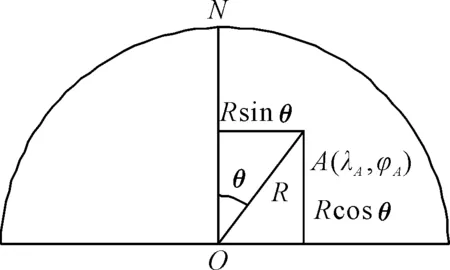
图1 参考物标沿经线、纬线分解示意图

假设A沿经线移动无限小的距离到达A′，纬度增加dφ，设参考物标A所在位置经线曲率半径为M，见图2.

则经线上对应的这一段微分弧长AA′为

(1)

图2 经线弧长计算示意图

由参考物标A沿经线到达任意一点B，设其纬度为φB，由φA至φB的经线长度Sm可通过对式(1)进行积分计算得出，即

(2)

将经线曲率半径M代入，经整理，得

(3)

式中：ae为地球椭球体长半径；e1为子午椭圆的第一偏心率;其余各参数计算方法及数值为

(4)

当B点纬度φB取：

φΒ=φΑ±1°

(5)

即可计算出参考目标A沿经线移动1°所对应的弧长DY.

因此，本船至参考点A的纬度差Δφ为

(6)

本船的纬度φ0即为

φ0=φA±Δφ

(7)

同理，可以推算出本船距离参考目标的经度差，由参考物标A沿纬度圈到达任意点C的距离Sn为

Sn=r(λC-λA)=NcosφΑ(λC-λA)

(8)

式中：r为纬度平行圈半径；N为卯酉圈曲率半径.

(9)

取λC-λA=1，利用式(8)，即可得到参考物标A沿纬度圈移动1°所对应的弧长DX.

本船与参考物标A的经度差Δλ为

(10)

本船的经度λ0为

λ0=λA±Δλ

(11)

2 雷达定位模型精度测算

为了检验前述船位推算数学模型的定位精度，通过在实验室雷达设备上设置不同距离、方位的参考目标，通过游标提取参考物标的位置数据、相对于本船的距离、方位数据，代入船位推算数学模型，分别推算出本船船位，与本船的真实船位进行比对，测算出雷达定位模型的理论定位精度.

以3 n mile量程为例，分别在与本船相对方位为45°，135°，225°，315°的1，1.5，2，2.5，3 n mile处设置参考物标，设定参考物标位置见图3，对应推算船位与真实船位误差结果见图4a).

同样对于6 n mile量程的情况，分别在与本船相对方位为45°，135°，225°，315°的1，2，3，4，5，6 n mile处设置参考物标，对应推算船位与真实船位误差结果见图4b)，为了便于3 n mile量程档的定位精度进行比较，将3 n mile和6 n mile的数据同时绘制于一张图上.

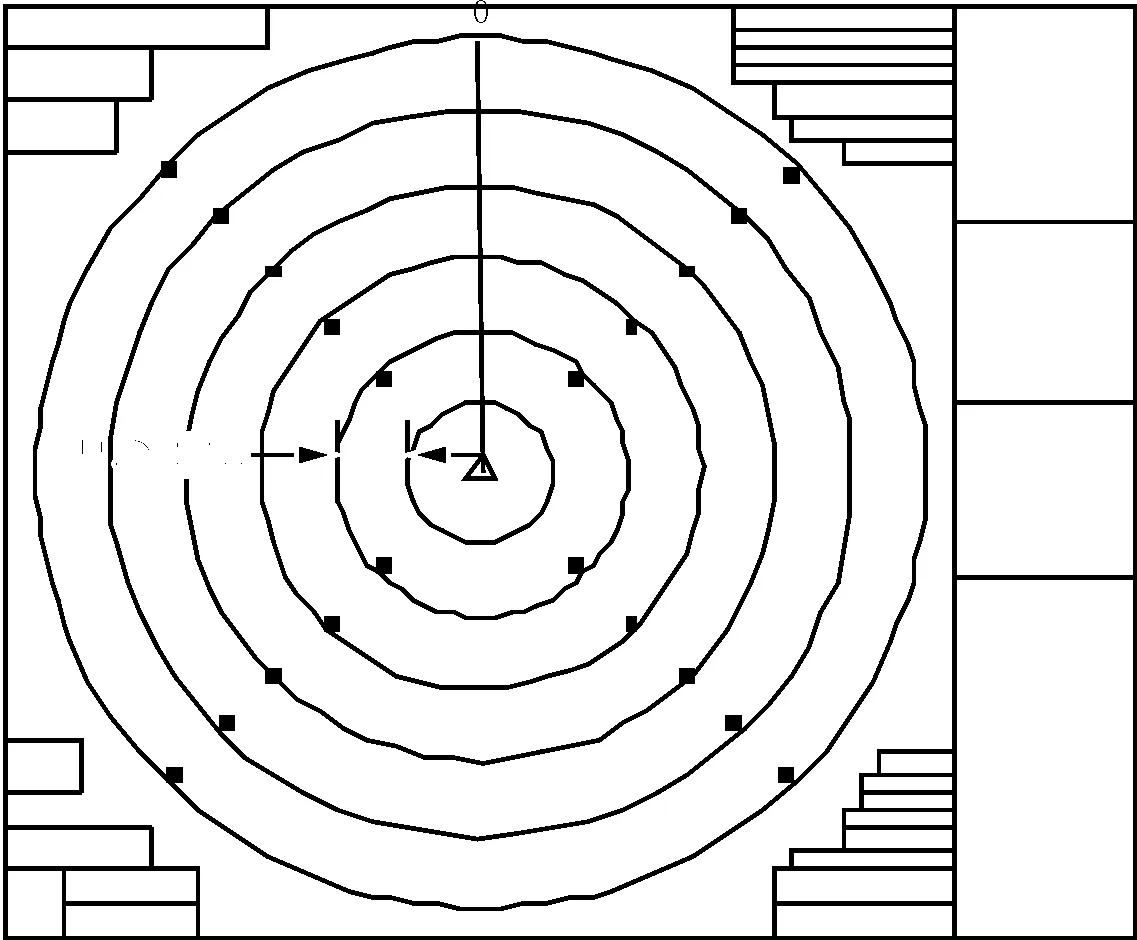
图3 3 n mile量程测试参考物标位置示意图

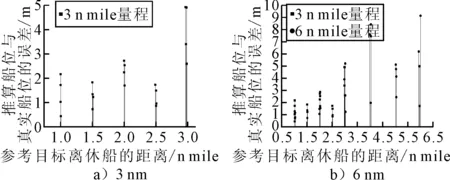
图4 3 n mile和6 n mile量程定位精度测算结果图

在3 n mile量程档选择参考物标，使用本数学模型定位的理论误差在5 m以内.

而6 n mile量程档选择参考物标，使用本数学模型定位的理论误差在10 m以内.

进一步在不同雷达量程下进行实验，设定不同距离、方位的参考物标，获得多组推算船位与真实船位之间的误差数据，结果见图5.

由图5的测算结果可知：

1) 在雷达目标跟踪范围内，即当参考物标距离船舶小于32 n mile时，定位误差保持在45 m以下，雷达定位数学模型精度较高，能满足特殊情况下船舶定位的精度需求.

2) 参考物标距离本船越近、量程设置越小，雷达定位数学模型精度越高.

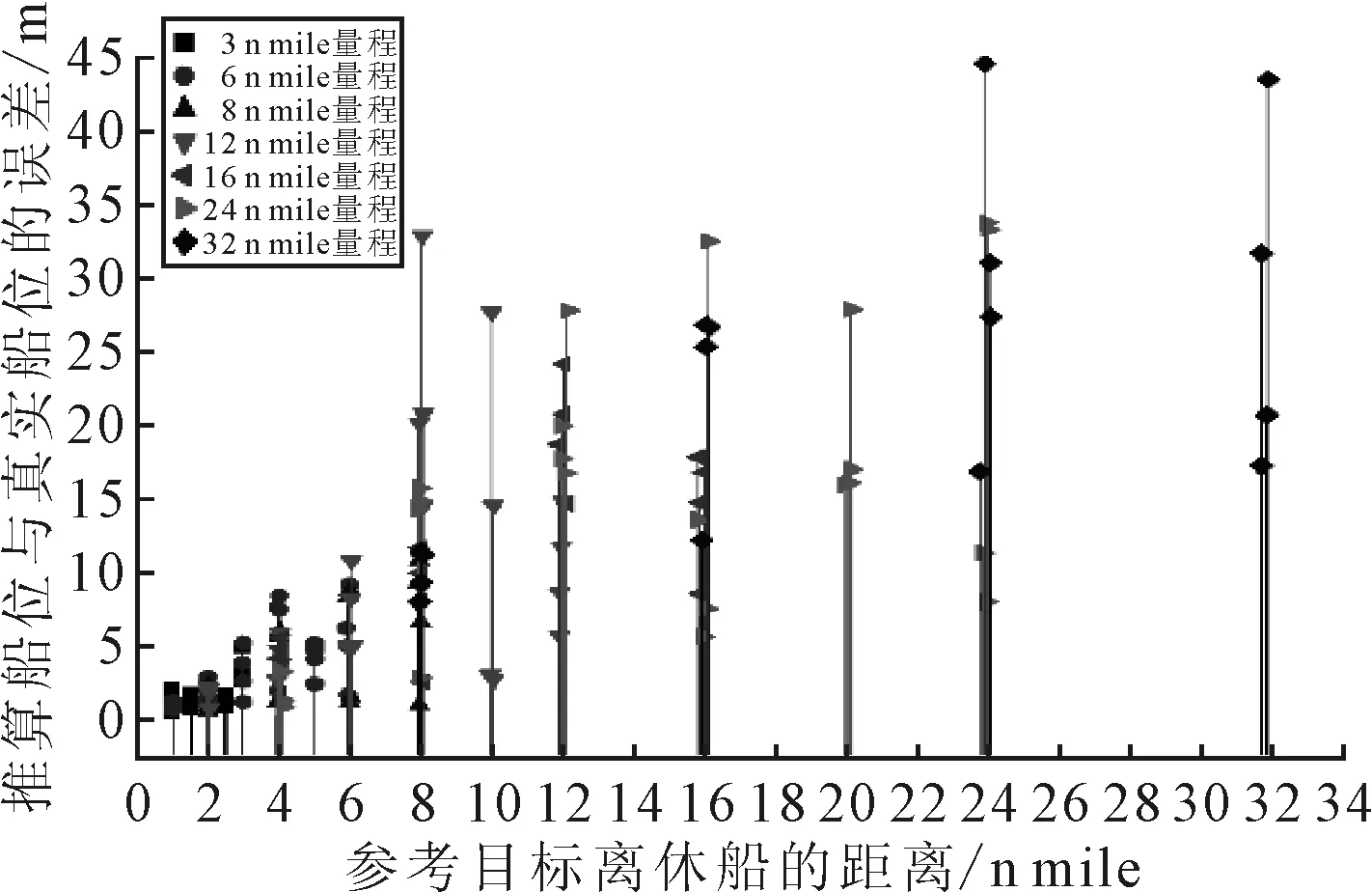
图5 定位精度测算结果汇总图

3 实船雷达数据定位精度测试

在实际使用雷达定位时，还必须考虑雷达测距、测方位、目标闪烁等随机误差的影响，雷达实船定位精度会低于理论定位精度.由于船舶在极地航行时，多行驶在沿岸航线，航线附近岛屿、灯塔等参照物较多，为了测试实际使用时雷达的定位精度，笔者在“长航福海”和“长航幸海”号船舶航行时，使用雷达分别选取固定参考目标进行了捕捉，获得连续的目标跟踪(target tracking，TT)数据，使用雷达定位模型计算出船位并与GPS真实船位进行了对比，测算实船雷达定位精度.

在“长航福海”上选取江苏南通龙爪岩作为定位参考物标，船舶在内河航行时，选取小量程(4 n mile)、近距离参考物标，偏心显示可以选择距离本船更远物标.

分别将定位参考物标的游标数据和TT数据代入雷达定位模型计算出理论定位船位和实际定位船位，定位精度结果见图6，理论定位精度为8 m以内，实际定位精度为20 m以内，且波动较大，符合船舶航行时使用雷达探测物标数据具有随机误差的特点.

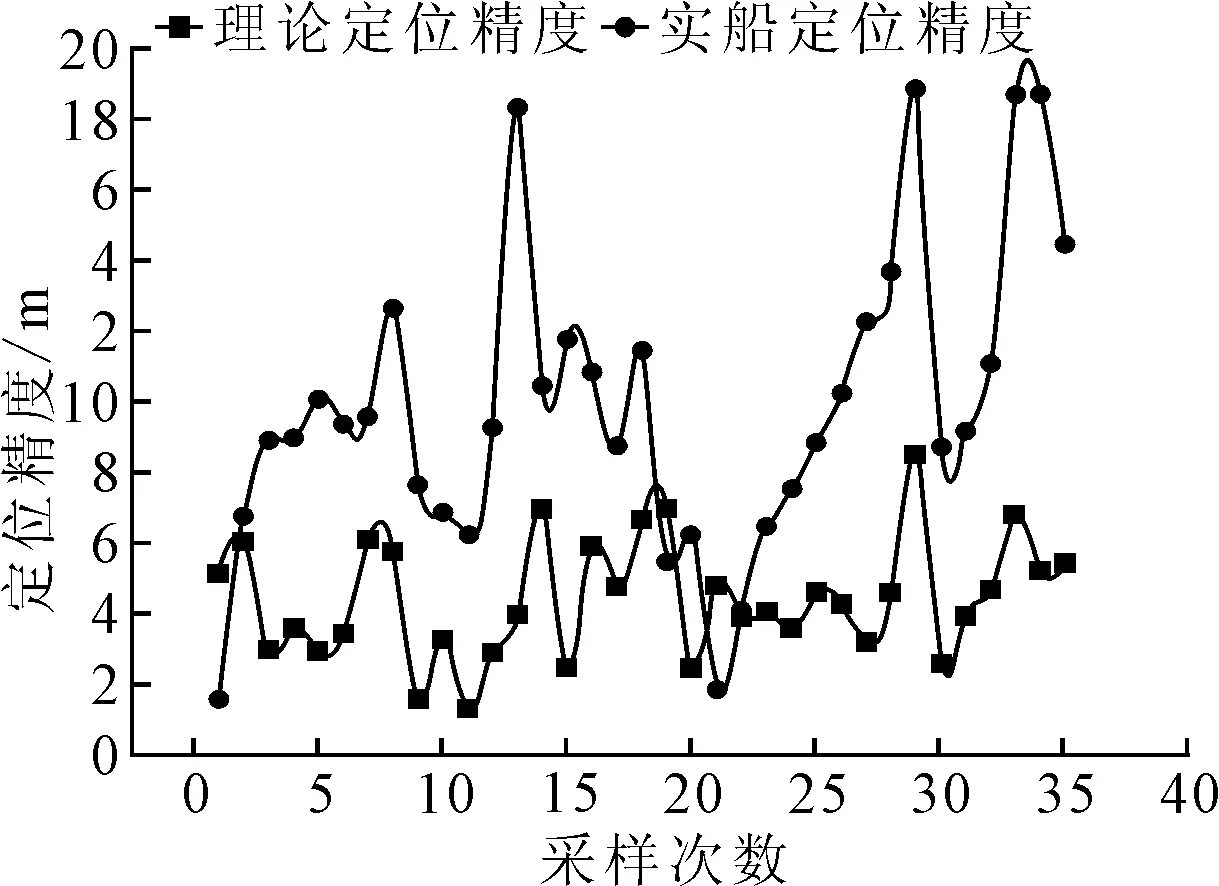
图6 “长航福海”雷达理论定位精度与实船定位精度对比图

在“长航幸海”上选取青岛大公岛作为定位参考物标.船舶在海上航行时，可以选取大量程档进行测试(12 n mile)、测试的定位精度结果见图7，显然12 n mile档量程的定位误差比前面4 n mile档量程定位误差要大，所以条件许可的情况下，尽可能地选择近距离目标作为定位参考物标.此外，当船舶航行时，参考目标相对船舶的位置由左前方、正横、侧后方变化时，雷达电磁波照射参考物标的中心位置有所移动，会带来较大误差.

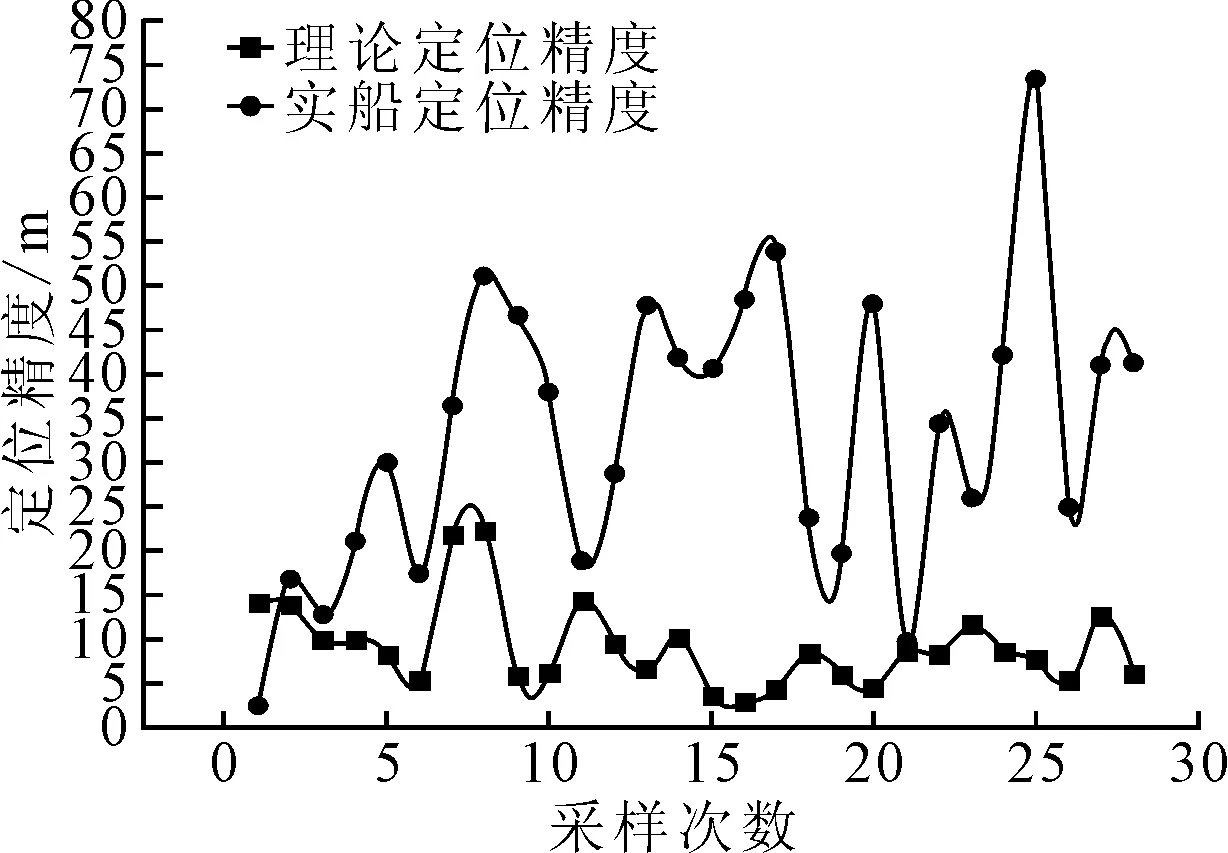
图7 “长航幸海”雷达理论定位精度与实船定位精度对比图

4 自动雷达定位系统实现方法

在雷达上捕获目标之后，TT目标的相关参数，包括到本船的距离、方位等输出至屏幕显示，因此可以通过串口将雷达与PC机连接，并通过计算机编程依据NMEA0183协议提取TT目标的相关参数，代入前述雷达定位模型，实现自动计算船舶位置数据.

选择周围静止物标作为定位参考物标，通过雷达捕捉使其成为跟踪目标TT，在输入参考物标的经纬度之后，程序可以输出船舶的经纬度数据，实现船舶的自动雷达定位，自动雷达定位工作框图见图8.

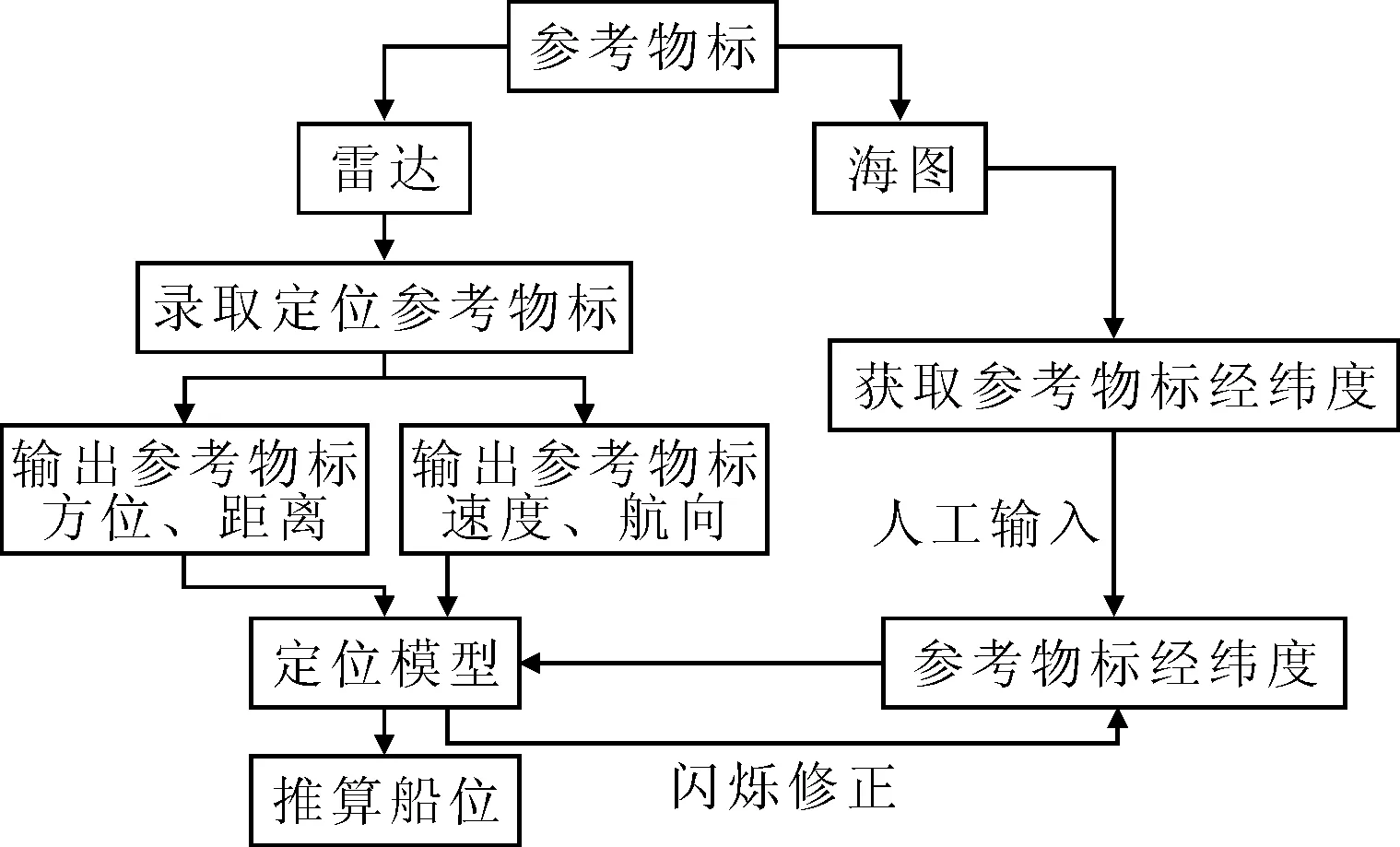
图8 自动雷达定位程序工作框图

5 雷达定位精度影响因素及对策

5.1 参考物标测量点的选择

雷达定位时，参考物标的初始位置值是操作人员从海图上估计测量点后提取的，与参考物标的雷达图像位置数据难以精确匹配，导致通过定位模型推算后的船位也会产生误差.

在雷达上选择某一固定参考物标，在海图上查找到该物标的初始位置值和参照GPS数据精确获得初始位置值分别输入到定位模型中得到的定位精度实验结果参见图9，前者定位精度均值40 m，后者则为10 m，显然，参考物标初始位置的精确与否对雷达定位精度有较大的影响.

图9 参考物标取值不同的雷达定位精度对比图

为了减少参考物标输入的初始位置与实际位置之间的误差，船用雷达定位时精确选择参考物标测量点的几个要点：①考虑船舶与定位参考物标的相对位置和角度选择参考物标测量点；②使用者对雷达探测目标的知识和经验；③雷达捕获参考物标稳定跟踪3 min之后，待输出数据精度提高到一定程度后再进行定位；④GPS正常时，参考GPS数据提取参考物标测量点值，并对固定航线的常用参考物标位置信息进行记录存档备用.

以海事雷达作为定位参考物标，对VTS监控水域的船舶定位时，由于海事雷达位置精确已知，所以可以获得更高的定位精度.

5.2 跟踪物标回波闪烁

雷达在跟踪参考物标的过程中，由于参考物标与雷达之间的距离、方位,以及雷达跟踪目标处理等因素的影响，导致雷达捕获到物标后，雷达电磁波照射参考物标的中心位置有所飘移，物标回波产生闪烁现象，即固定参考物标在雷达上变成漂移物标，观察跟踪物标的SOG和COG值的变化可以得到验证，见图10.

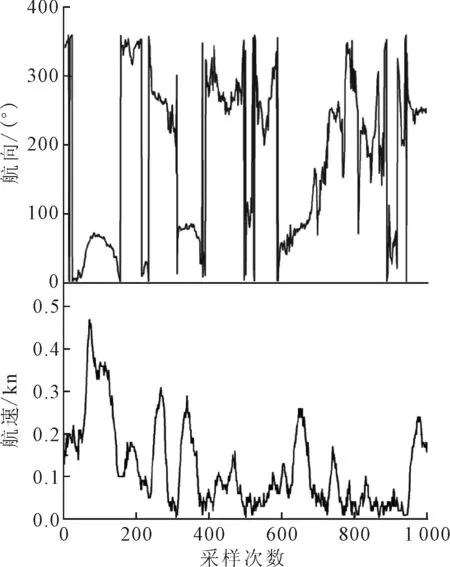
图10 参考物标漂移速度和航向变化图

虽然每次漂移的速度较小，单次定位的影响不大，但是在连续的定位过程中误差会累积增加，导致雷达定位误差不断增大.

为了减少雷达在跟踪参考物标的过程中由于目标闪烁而造成的精度影响，显然不能把参考物标作为一个固定物标处理.本研究使用了参考物标漂移位置点自动跟踪的方法提高定位精度，即每次定位时以原来的参考物标位置为起点，使用SOG、COG计算出参考物标漂移后到达的位置点作为定位参考物标的新位置值，代入定位模型，实现自动跟踪参考物标位置漂移变化的雷达定位方式.参考物标位置为固定值和动态值的定位精度结果以及对应的漂移速度见图11.

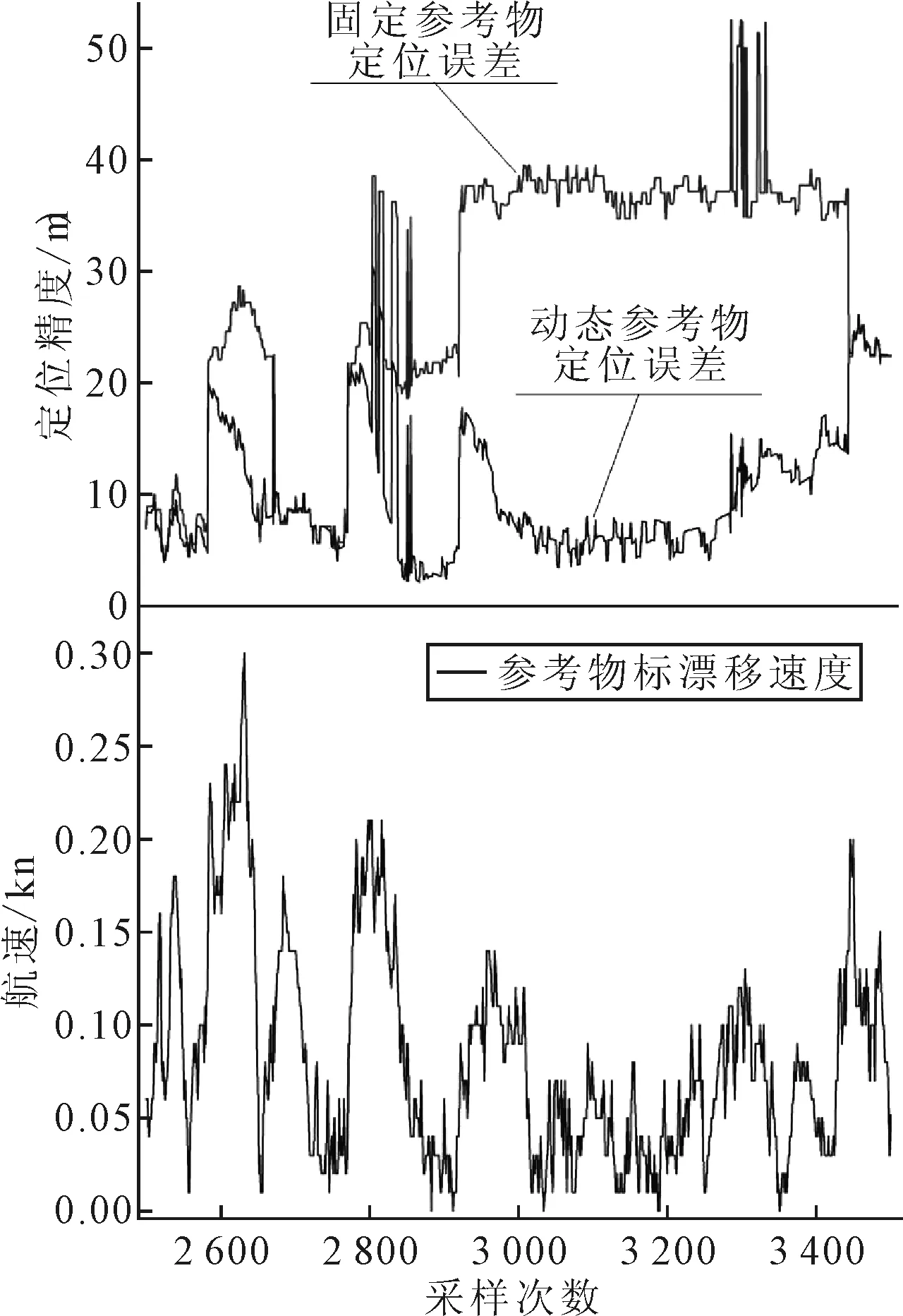
图11 参考物标位置固定取值和动态取值的定位精度

当漂移速度较大时，参考物标漂移距离较大，远离原来的位置点，而仍然以原来的位置点(固定值)进行定位的误差会越来越大，由于漂移具有一定的随机性，漂移一段时间后，测量点有可能会回到原来的初始位置，定位误差减小.而采用漂移后的位置点(动态值)进行定位的方式则可以有效地减少漂移带来的影响.比较两者结果可知：采用参考物标漂移位置点自动跟踪进行测量点位置修正的方法，受参考物标位置漂移带来的影响较小，基本能保持在初始时的定位精度.

6 结 束 语

本文通过构建船位推算数学模型，在获取参考物标位置信息的基础上，利用雷达跟踪物标功能，推算船舶船位；采用实验测算和实船雷达数据测试的方法，验证了高精度自动雷达定位的可行性，开发了一款自动雷达定位应用软件，并使用该软件对自动雷达定位精度进行了测试，分析了雷达定位精度影响因素及提出相应的控制对策，实现了在卫星定位出现异常的情况下，为极地航行船舶提供一种快速、连续、准确的替代定位手段，同时本方法也可以扩展为海事雷达监管船舶提供定位服务.

通过在实验室多次试验证明：在精准获取参考物标初始位置的条件下，本研究提出的自动雷达定位方法可以获得较高的定位精度.在实船上开展进一步测试工作是课题组后续研究的课题.