指路标志与路面文字协同设置安全距离研究*

裴玉龙 曹永臣

(东北林业大学交通学院 哈尔滨 150040)

0 引 言

随着城市经济的迅速发展，汽车保有量的增大，城市基础设施的建设明显加快，城市道路网越来越复杂，我国虽已颁布文献[1-2]等国家标准以期科学性、规范性，以及系统性地管理城市道路交通标志与标线设置，但交通指路标志需要表达的信息越来越多，同时驾驶人的视认能力有限，例如，新的地名、路名大量涌现，造成个别路段交通提示标志信息过多，或因为停车位车辆或道边树木的遮挡，驾驶人没有足够时间识别、理解这些信息，从而影响道路交通安全.

国内外专家学者对交通标志和标线的和合理布设以及驾驶人的视认特性，进行了大量的研究.Byshov 等[3]系统地将道路标线与特定的速度限制相关联可能是提高提示效率的有效方法.Costa等[4]从注意力不集中、驾驶行为的自动性等方面研究路边直立式标志下驾驶人的视认特性.Charlton[5]研究在驾驶人在弯道驾驶时，四种警告标志组合和几种道路标线组合对于车辆速度和车道位置的影响.徐志等[6]以Ltti的视觉注意模型为基础，建立了针对交通标志的注视点预测模型，对复杂交通标志的注视点预测具有良好的精度.熊坚等[7]提出了一种通过驾驶动态模拟心理学实验评价城市指路标志认知性的方法．建立了用于驾驶模拟实验的路网及相关的指路标志系统.姚裔虎等[8]针对现冰雪地区公路弯道，提出了冰雪道路弯道诱导标设置间距模型，进而得出减速限速和提醒标志设置的最佳位置.文献[2]在交叉口与路段上的交通标志和标线协调设置方面进行了更加细致的规定.

国内外对交通标志标线设置的安全距离和驾驶人视认效果有较详实的研究，但对二者协同设置的研究较少.由此，本文提出使用交通指路标志与路面文字协同设置的方法，选取城市主干路作为研究对象，将设置在路边的单悬臂式交通指路标志版面所表达的部分信息，以路面文字的形式设置在指路标志前方，以对道路信息进行重复表达.在车辆行驶过程中，驾驶人的视认顺序为“路面文字→指路标志”.本文提出协同距离的概念，为路面文字与交通指路标志顺次设置时，使得驾驶人对指路标志的视认时间最少时二者的间距.

1 驾驶人视认过程分析

1.1 研究的前提假设

本文的研究内容为城市主干路上路面文字与指路标志的协同设置，为方便实验和研究的顺利进行，需先做出以下前提假设：①研究对象为城市主干路，道路设计车速为40，50和60 km/h，指路标志的尺寸取140 cm×100 cm；②研究范围为双向6车道道路，单车道宽度设定为3.25 m；③参与实验的被试人员生理、心理皆为正常状态.

1.2 驾驶人视认过程

驾驶人视认过程见图1，驾驶人在A点视认设置在D点的路面文字并在B点视认结束，即为路面文字认读点，AB为视认距离，车辆从A点行驶到B点所使用的时间为驾驶人对路面文字的视认时间.驾驶人到达C点时，路面文字从视野中消失.

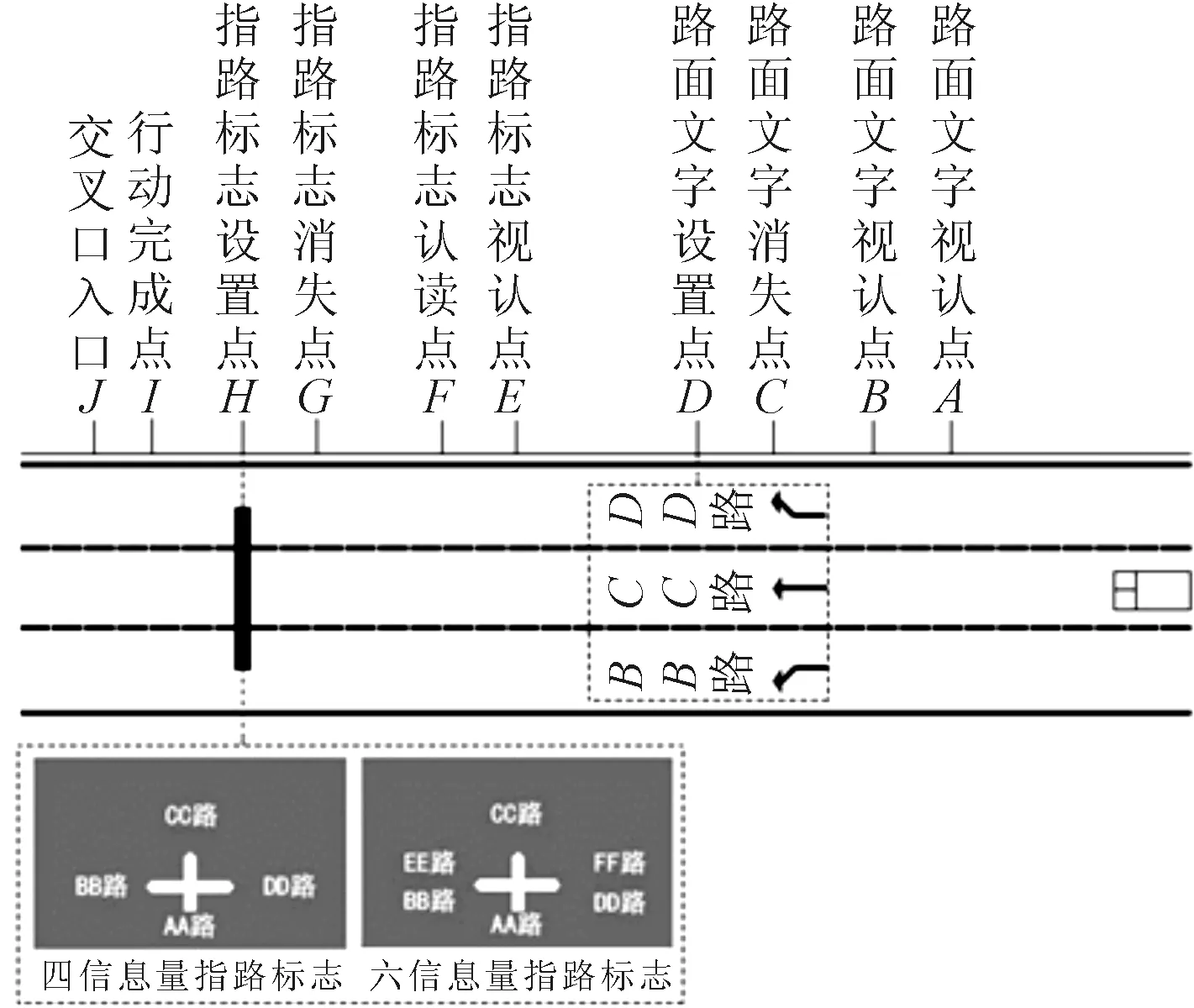
图1 驾驶人视认过程

驾驶人在E点视认设置在H点的指路标志(包括四信息量和六信息量指路标志)，并在F点视认结束.DH为路面文字和指路标志的设置间距S1.EF为指路标志视认距离(E点或F点相对于于D点的先后位置不确定)，车辆从E点行驶到F点所使用的时间为驾驶人对指路标志的视认时间，驾驶人进行决策及操作行为.

驾驶人到达G点时，指路标志从视野中消失，并在I点时行动完成，J点为交叉口的入口处，HJ为指路标志前置距离S2，DJ为路面文字的前置距离S3.则路面文字和指路标志的设置条件应满足：

S1+S2=S3

(1)

式中：S1为指路标志和路面文字设置间距，m；S2为指路标志前置距离，m；S3为路面文字前置距离，m.

1.3 指路标志设置高度

由于车辆高度相较于交通标志较低，a为驾驶人的竖直视角，根据文献[9]可知，当a>8°时，驾驶人视认能力迅速下降，因此取8°为驾驶人竖直视角的临界值；h为驾驶人视点高度，取1.2 m；d为驾驶人与指路标志的垂直距离；H为交通标志设置高度，等于h和d之和，取5.2 m；X为标志从驾驶人视野消失时，驾驶人与指路标志的水平距离，X与d的关系见式(2).本文研究的交通指路标志为单悬臂式，驾驶人与指路标志的几何关系见图2.

d=Xtana

(2)

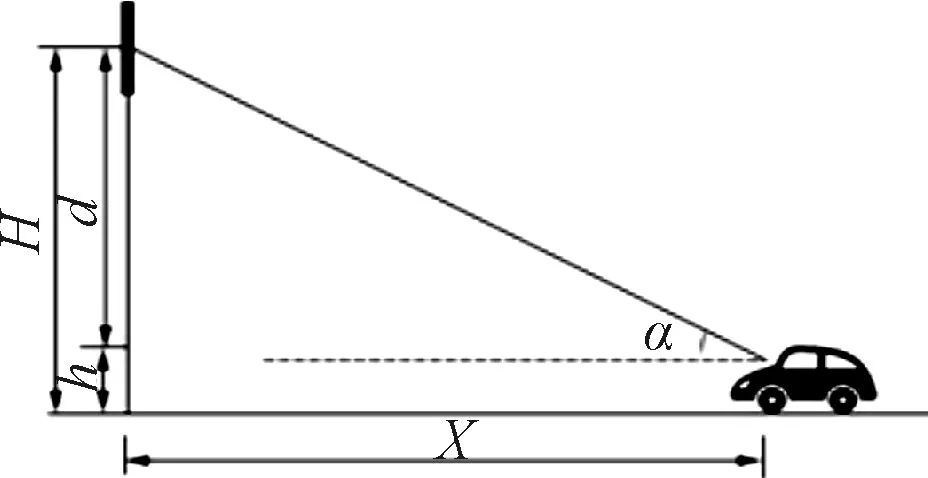
图2 驾驶人与指路标志的几何关系

1.4 指路标志前置距离

驾驶人认读指路标志后，操纵车辆变换车道过程见图3，M1～M6为道路上几个车辆行驶状态发生改变的位置.车辆经过视认点—认读点—思考点—消失点过程，达到车辆变道的第一个决策点F，车辆经过两组决策点和执行点后完成两次变换车道的操作，最终到达变道完成点J点.则指路标志前置距离模型S2[10]为

(3)

式中：S2为指路标志前置距离，m；(n-1)L为变换车道所必需的距离，m；L为改变一次车道所需距离，m；n为车道数；为减速、改变方向所必需的距离，m；v1为接近车速，m/s；v2为交叉口处车速，m/s；t为驾驶员的决策时间，s；a为车辆减速度，m2/s；l为视认点和指路标志的间距，m.

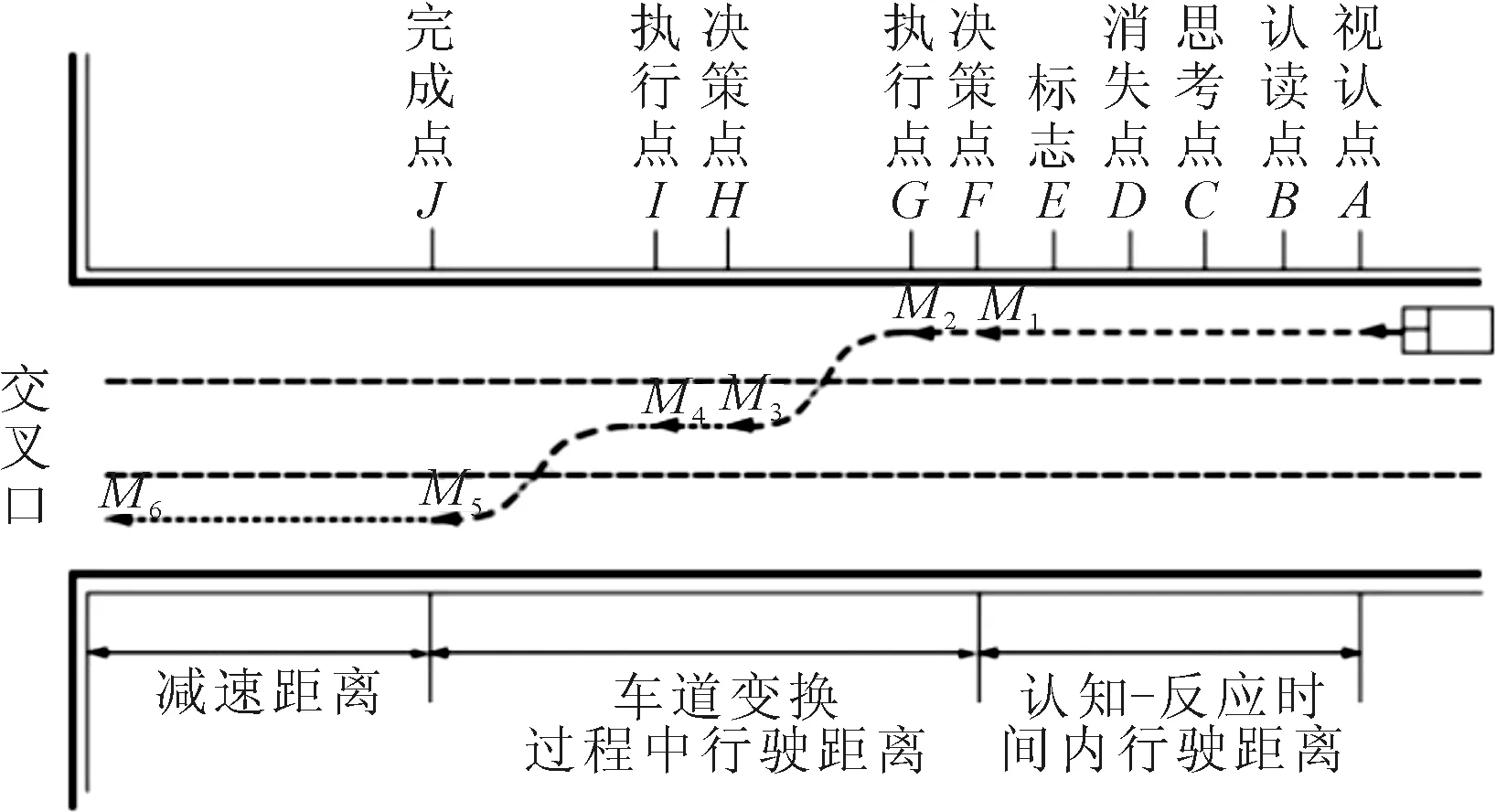
图3 车辆变换车道过程

参照文献[1]中速度值所对应的前置距离，以及杨冰浩等[11-14]的研究成果，并结合式(3)，得到设计速度对应指路标志前置距离的建议值见表1.

表1 指路标志前置距离

2 标志标线协同设置实验

2.1 实验设计

1) 使用视频制作软件Adobe Premiere，结合余曼等[15]的研究成果对指路标志和路面文字进行设计，制作城市主干路驾驶场景视频作为实验材料，按标志标线设置方式分为两类：仅指路标志作用、路面文字和指路标志协同作用.

2) 将实验材料中，指路标志表达的信息数量分为四信息量和六信息量两类，路名信息位置设计见图4.对于四信息量指路标志，路面文字重复位于图4a)中位置2、位置3、位置4的路名；对于六信息量指路标志，根据文献[2]中8.1.4节的要求，图4b)中位置5和位置6为远信息，位置2和位置4为近信息，也就是下一次左转或者是右转时将进入的道路，所以路面文字重复位于图4b)中位置2、位置3、位置4的路名.

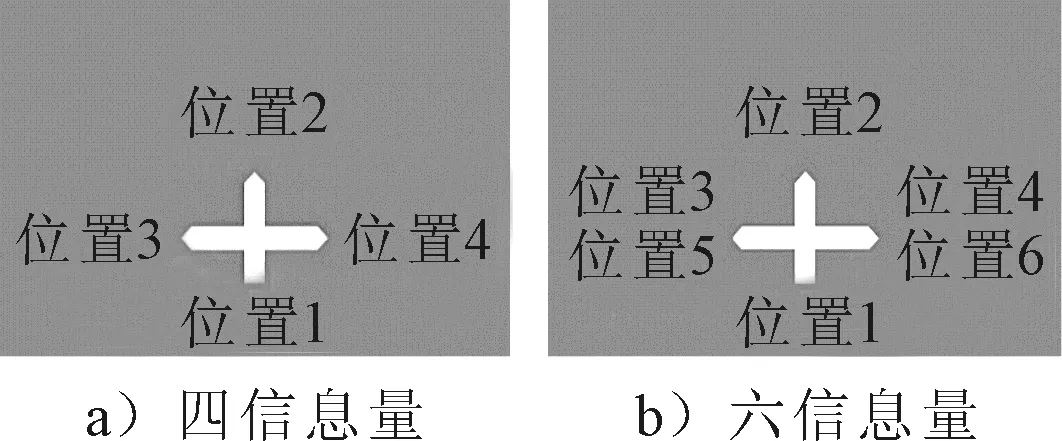
图4 路名在指路标志版面的位置

2.2 实验过程

1) 选择24人作为被试人员进行实验.实验前，要求被试人员完成基本信息的调查问卷，问卷内容包括年龄、性别、有无驾龄、有无近视、是否患病等，剔除其中不符合条件的被试人员.

2) 向被试人员解释实验过程，以确保所有被试人员在了解实验要求和内容.

3) 使用投影仪播放实验材料，被试人员观看视频并按要求作出响应(用秒表记录时间节点)，其中仅指路标志出现的驾驶场景见图5,路面文字和指路标志顺次出现的驾驶场景见图6.

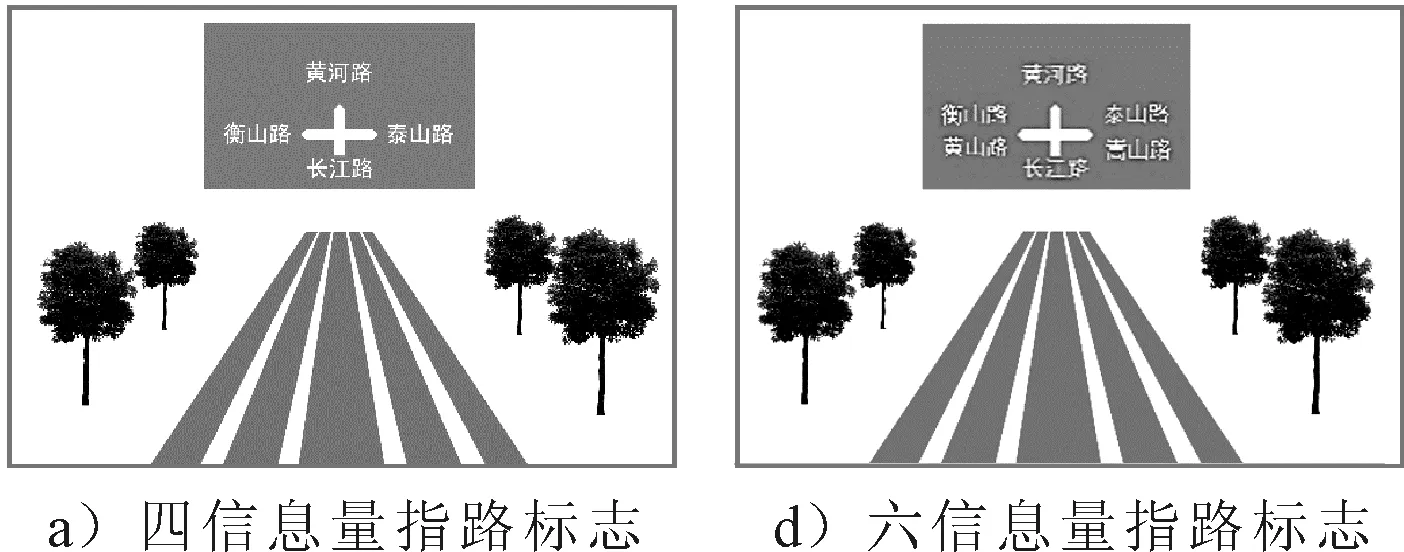
图5 仅指路标志实验材料

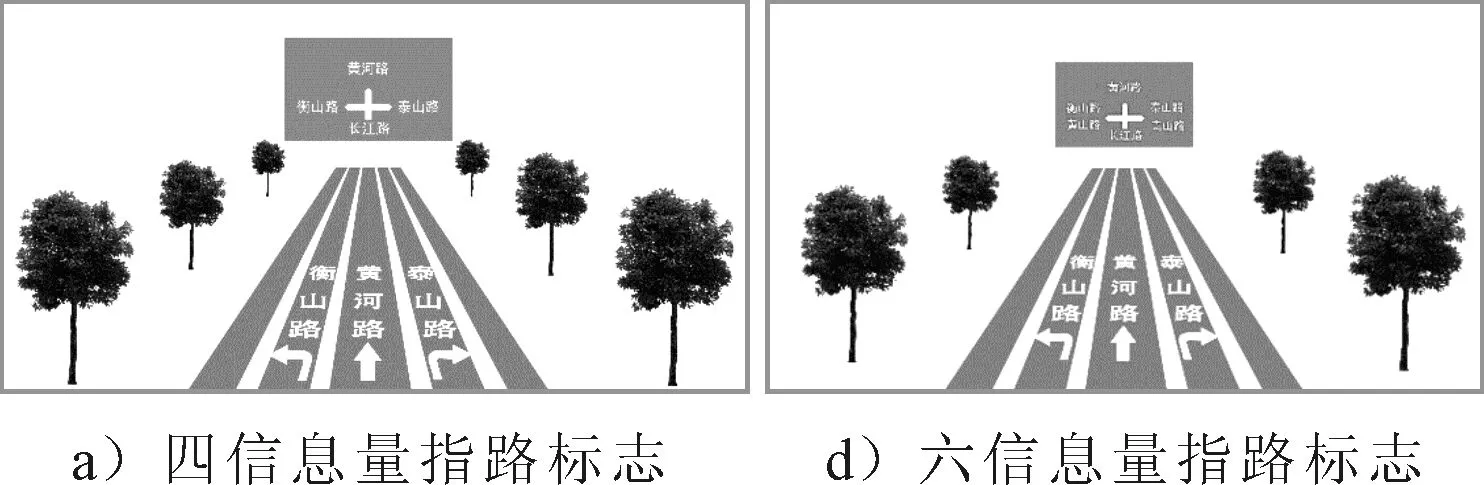
图6 路面文字和指路标志顺次出现实验材料

4) 将测试人对指路标志视认时间、测试人基本信息、路面文字和指路标志设置间距等原始数据进行整理，导入SPSS软件进行分析，依据统计结果将反应时间异常的数据定义为反应错误数据，在进行反应时间分析时，反应错误的数据不做统计.

3 路面文字与指路标志协同设置距离优化

3.1 剔除不相关因素

筛选出性别、有无近视、有无驾龄等不相关因素.对数据中的样本进行t检验，结果分别见表2～4.

表2 性别独立样本检验

表3 有无近视独立样本检验

表4 有无驾龄独立样本检验

检验结果表明测试人的性别、有无驾龄以及有无近视对实验结果没有影响，结合袁黎等[16]的研究成果，应将该类因素剔除，表明本文属于基础研究，性别、有无驾龄、有无近视等因素对实验结果得到的规律没有影响.

3.2 信息量和信息位置对协同设置优化程度的影响

比较仅指路标志、路面文字和指路标志协同两种情况下驾驶人对指路标志的视认时间并求得二者差值，即视认时间差，将视认时间差分为四信息量指路标志和六信息量指路标志两种情况[17].对信息量和视认时间差两组数据进行独立样本t检验，得到独立样本检验见表5.其中T=-6.701、P=0.000，表明指路标志信息量与视认时间差之间显著相关.

四、六信息量情况下，将视认时间差按路名所在的版面位置分为位置2、位置3、位置4三组，比较路面文字和指路标志协同设置对指路标志视认时间的优化程度，即比较三个位置在这两种信息量情况下的视认时间差，见图7.由图7可知，相对于四信息量指路标志，设置于六信息量指路标志前的路面文字对驾驶人视认效果的改善作用更为显著，且改善程度为位置4>位置3>位置2，其原因为三个位置上协同设置对四信息量指路标志的优化程度相近，主要在0～0.6 s，而对六信息量的优化程度为0.2～0.6 s(位置2)、0.4～0.9 s(位置3)、0.6～1.2 s(位置4)，优化程度有较大差别.

表5 独立样本检验

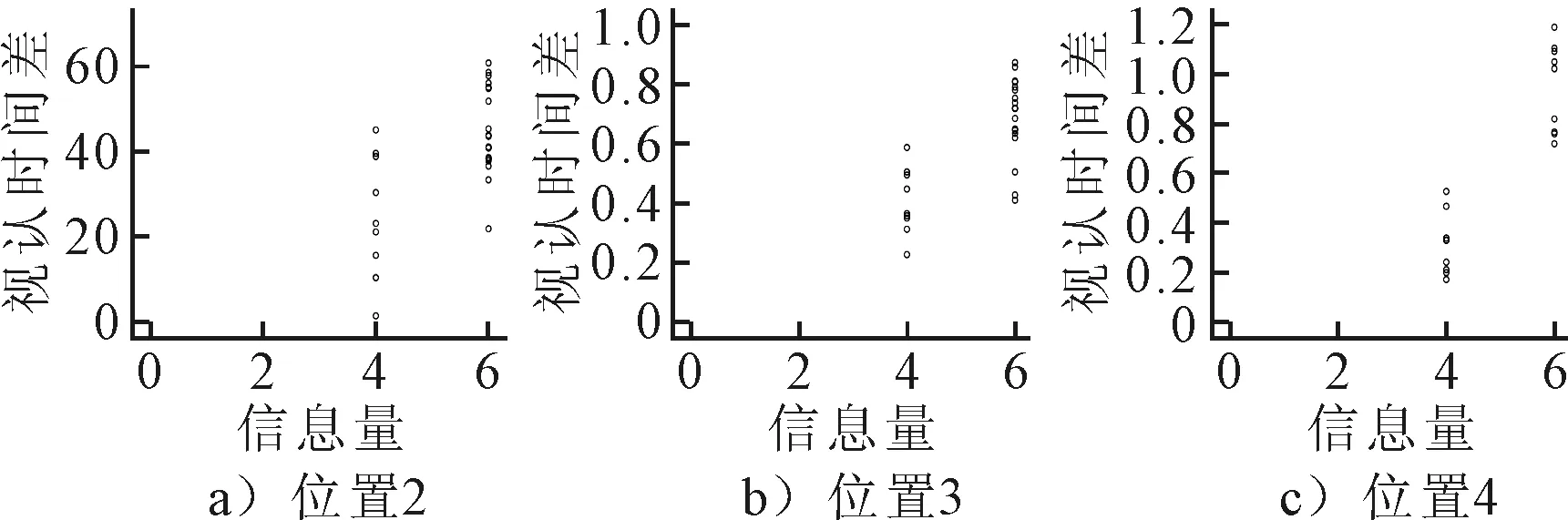
图7 四信息量和六信息量视认时间差

3.3 路面文字与指路标志最佳设置间距研究

分析设计车速为40，50，60 km/h，并分别使用四信息量、六信息量指路标志的情况下，路面文字与指路标志设置间距和驾驶人指路标志视认时间的关系.将实验得到的6种情况下设置间距与驾驶人视认时间两组数据，依设计车速分组进行拟合，得到2组拟合结果见图8～9(v为设计车速)，其中，视认时间为驾驶人从看到指路标志到认读标志牌信息所使用的时间，设置间距为路面文字与指路标志二者所处位置间的距离.可以看出，起初视认时间随设置间距的增大而减小，但在设置间距达到某一数值后，视认时间达到最小值，之后则随设置间距的增大而缓慢增大，表明路面文字和指路标志的设置间距并非绝对的越大越好，而是存在一个最优解，即最佳的设置间距.

将6种情况下的拟合优度按指路标志信息量分组表示，结果见表6～7，拟合程度、F检验、显著性均皆较好，表明拟合程度较好，其结果可用于进一步分析，得到设置间距与视认时间的关系模型见式(4)～(5).

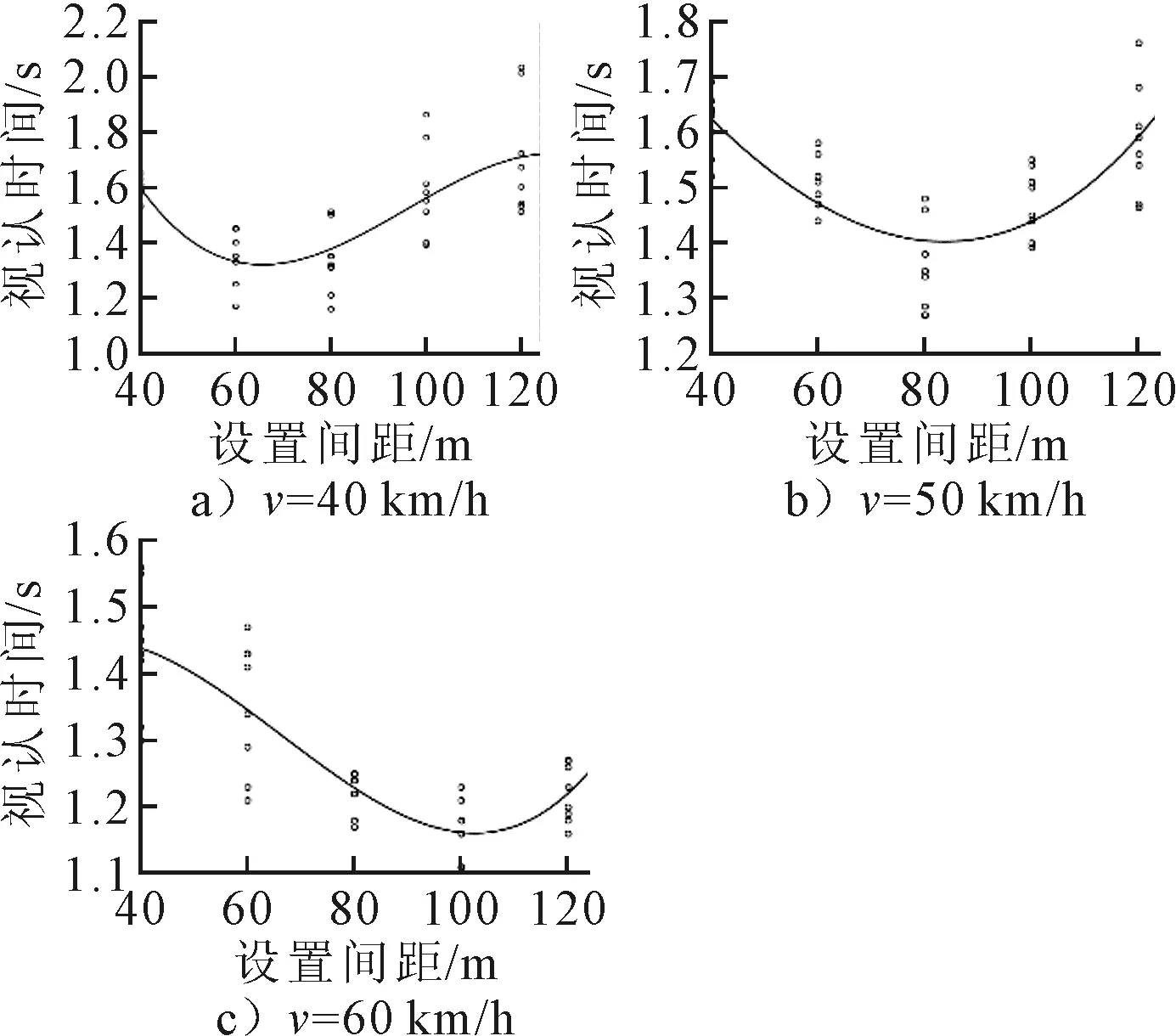
图8 四信息量情况下的拟合结果

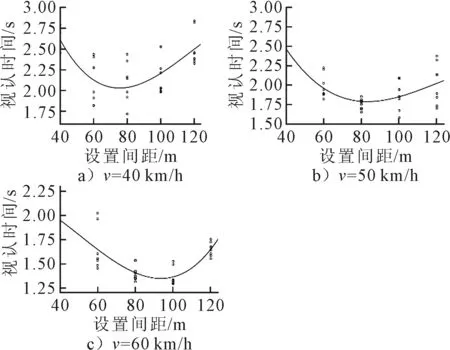
图9 六信息量情况下的拟合结果

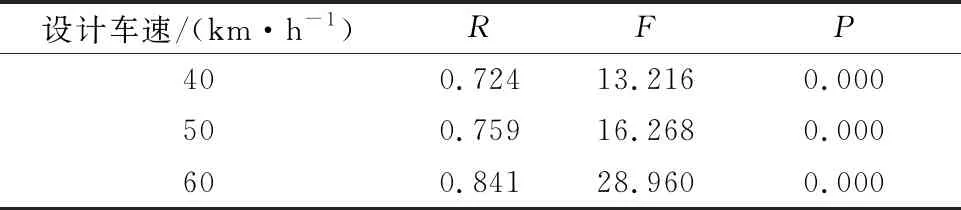
表6 四信息量指路标志拟合优度

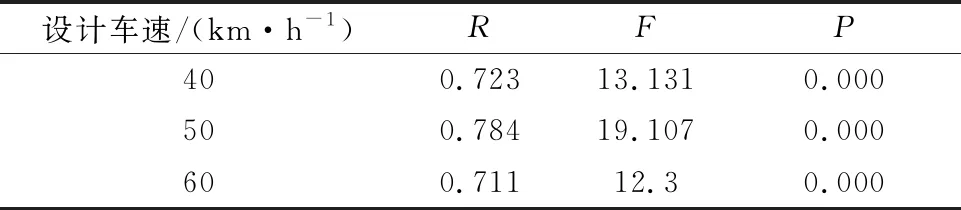
表7 六信息量指路标志拟合优度

四信息量指路标志与路面文字设置间距模型：

(4)

六信息量指路标志与路面文字设置间距模型：

(5)

式中：S1为路面文字和指路标志的设置间距，m；t为驾驶人对指路标志的视认时间，s；v为设计速度，km/h.

使用MATLAB数学软件计算式(4)～(5)的极值，得到在不同设计车速、指路标志信息量的情况下，驾驶人对指路标志视认时间最少时，路面文字和指路标志的设置间距，作为最佳设置间距，即本文所提出的协同距离，结果见表8～9.

表8 四信息量情况下的协同距离

表9 六信息量情况下的协同距离

由表8～9可知，路面文字和指路标志的协同距离受指路标志信息量影响较小，但受设计车速影响较大，且呈正相关.不同设计速度下，对四信息量指路标志的视认时间差别不大，对六信息量指路标志的视认时间差别较大，且随设计车速的增大而减小.

根据式(1)得到各情况下路面文字和指路标志前置距离，见表10～11.

表10 四信息量指路标志和路面文字的前置距离

表11 六信息量指路标志和路面文字前置距离

4 结 论

1) 相对于四信息量指路标志，设置于六信息量指路标志前的路面文字对驾驶人视认效果的改善作用更为显著，且信息位于指路标志版面的不同位置，其改善程度不同.

2) 构建不同信息量、不同设计车速情况下，协同设置间距和驾驶人对指路标志视认时间的关系模型，并得到在各类情况下视认时间最少时，路面文字和指路标志的设置间距，作为最佳安全间距，即协同距离.