基于不同数值通量的间断Galerkin方法性能的研究
2020-08-25张小华
李 广,张小华
(三峡大学 理学院,湖北 宜昌 443002)
浅水波方程已经被广泛应用于海洋和水利工程以及地球物理流,如河流、潮汐、流动的水库和明渠等[1],该系统将其描述为带有附加源项的守恒律.然而对于双曲守恒律,即使具有光滑的初始条件和边界条件,也可能在计算域内产生不连续解[2].因此,浅水波方程的数值模型需要能够捕获这些不连续性,DG方法是一种解决这类问题的适当选择.它具有精度高、并行效率高和易于处理边界条件等优点,在计算流体力学的框架下,已经被广泛地应用于空气声学、粒状流、磁流体动力学、气象学、海洋学、湍流、粘弹性流动、浅水建模以及天气预报等领域.
最早的DG方法是由 Reed和Hill于1973年在一个报告中提出来的,并解出了与时间无关的中子输运线性双曲方程[3].Cockburn和舒其望等人对其发展作出了非常重要的贡献,即建立了一个易于求解且与时间相关的非线性双曲守恒律的框架[4-10].在这个框架中,时间离散使用的是高阶龙格-库塔(RK)格式,空间离散来自于有限元方法,数值通量一般使用的是Lax-Friedrichs通量,并且在时间步进格式中的每一步后都使用一次全局变分有界(TVB)限制器.
DG方法的一个重要组成部分是基于精确或近似黎曼求解器的数值通量,同时借鉴了有限差分法和有限体积法.一般情况下,通量的定义不是唯一的,取而代之的是一个数值通量.因此,必须选取一种正确的解,我们把这个解称为数值通量[11].通量的作用是运用所求方程的信息流动来保证所构造的DG格式的稳定性,数值通量的选取也是构造各种DG格式的关键,因此必须保证数值通量是相容的.关于数值通量的另一要求是选取的通量必须是单调的,即既要对第一变量非递减,又要对第二变量非递增[12].在大多数研究DG的文献中,Lax-Friedrichs 通量因其简单性而被广泛使用.本文主要研究使用基于各种不同数值通量的DG法在求解一维浅水波方程中的性能,比如Lax-Friedrichs通量[12-13]、Rusanov通量[14]、Harten-Lax-van Leer通量[2,15]以及Roe通量[2].
1 一维控制方程
在一维空间中考虑浅水波方程,其形式如下:
(1)
其中,h为水流深度,u为x方向上平均水深的速度,g是重力加速度,S0与Sf分别是底部床坡与斜坡摩擦,下标t和x分别表示关于时间t和坐标x的偏导数.该系统考虑了由于底部地形和斜坡摩擦引起的源项,还可以加入其他源项,比如粘性应力、科氏力、潮汐势力和风表面应力等影响.先将方程(1)改写成如下守恒形式为
其中,U=[h,hu]T为保守变量的向量,F=[f1,f2]T=[hu,hu2+0.5gh2]T是通量向量,源项向量是S=[0,gh(S0-Sf)]T,上标T表示矩阵的转置.一般情况下,假定稳态流动的斜坡摩擦在非定常流态下是有效的,其中n为曼宁粗糙度系数,于是底部与斜坡摩擦项可以分别近似为
2 DG方法
2.1 空间离散
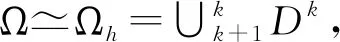
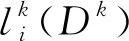

(2)
对K个单元都成立, 但是方程(2)还不能用于求解整体解. 假设试验函数光滑但跨界面不连续,对方程(2)关于空间变量分部积分,所得格式就是经典弱形式下的节点DG方法
(3)
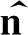
2.2 数值通量

2.2.1 Lax-Friedrichs (LF)通量LF通量是DG方法和高阶有限体积法最简单、应用最广泛的基本部分之一.然而,LF通量的数值黏性在标量问题的单调通量中也是最大的.其定义和最大波速度分别为
2.2.2 Rusanov(RUS)通量定义为

2.2.3 Harten-Lax-van Leer (HLL)通量Harten,Lax和Van Leer于1983年提出了HLL黎曼求解器,该求解器具有三个恒定状态,分别被两个波隔开.浅水波方程的HLL通量为

2.2.4 ROE通量一维矩形河道浅水流动的Roe通量函数为
Roe通量函数中的变量为
2.3 时间离散
时间步长被记为Δt,且Δt=tn+1-tn,则Un+1=U(t=tn+1).此处采用文献[13]中的三阶三步总变差递减-龙格库塔格式,也被称为保强稳定的龙格库塔格式.这种格式既能够保证高精度又能保证在时间积分过程中不会引进额外的振荡.因此,适用于浅水波方程的具有最优三阶精度的SSP-RK格式为
2.4 斜率限制器
即使在初始条件是光滑的情况下,非线性守恒律的解也会出现不连续甚至产生振荡,这给数值求解带来了很大的困难,所以在SSP-RK时间步进格式中每一步之后都使用一次斜率限制器是一种很好的选择.限制器既能够获得高效、可靠的重建策略,又能够获得更好的数值解,还能节省计算成本.虽然可以在DG方法中使用多种限制器,但是对各种不同的问题,没有一种确切的限制器明显优于其他限制器[11].
2.4.1 Minmod梯度限制器(MD)梯度限制器重构的方法是基于守恒定律的单调上游格式和分段抛物线法.为寻求一个具体修改解的局部均值以保证TVDM性质,定义minmod函数m(·)为
如果k个变量取为k个单元上解的梯度,那么当所有梯度不同号时,minmod函数将梯度设置为零,这表明一个振荡;否则,minmod函数取为最小的梯度.
2.4.2 改进的梯度限制器(MM)简单利用梯度限制器可能会破坏光滑区域上的高阶精度,而广义梯度限制器虽然可以改进在解的光滑区域处的精度,但是不能克服在局部极值附近精度的损失.本文使用改进的一种minmod梯度限制器.其处理方法是放松全局变分的衰减条件,只要求平均的全局变分有界,即TVBM条件.对此,需要稍微修改minmod函数m(·)的定义为
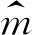
则满足TVBM条件.常数M是在局部极值处二阶导数的一个上界,一般取M=20 .
3 数值实验
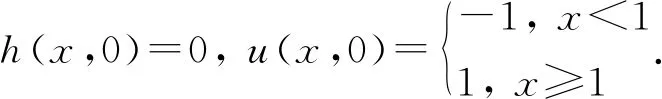
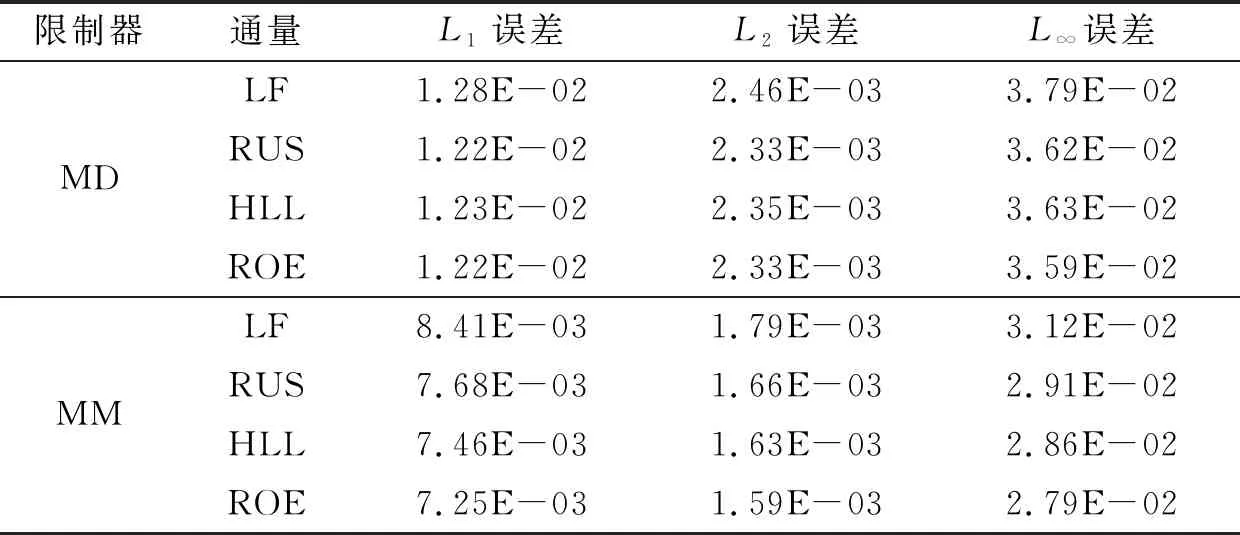
表1 DG方法计算水深h所得的L1, L2和L∞误差
表1分别提供了基于四种不同通量的DG格式关于水深h的L1,L2和L∞误差.将通量为“X”的DG方案表示为DG—X,例如通量为LF的DG方案表示为DG—LF.当使用梯度限制器时,其他方案关于水深h的L1,L2和L∞误差分别约是DG—LF方案的95%,96%,95%.当使用改进的梯度限制器时,其他方案关于水深h的L1,L2和L∞分别约是DG—LF方案的91.3%,88.7%,86.2%.相比之下,当限制器相同时,使用ROE通量计算所得的误差在所有方案中最小.
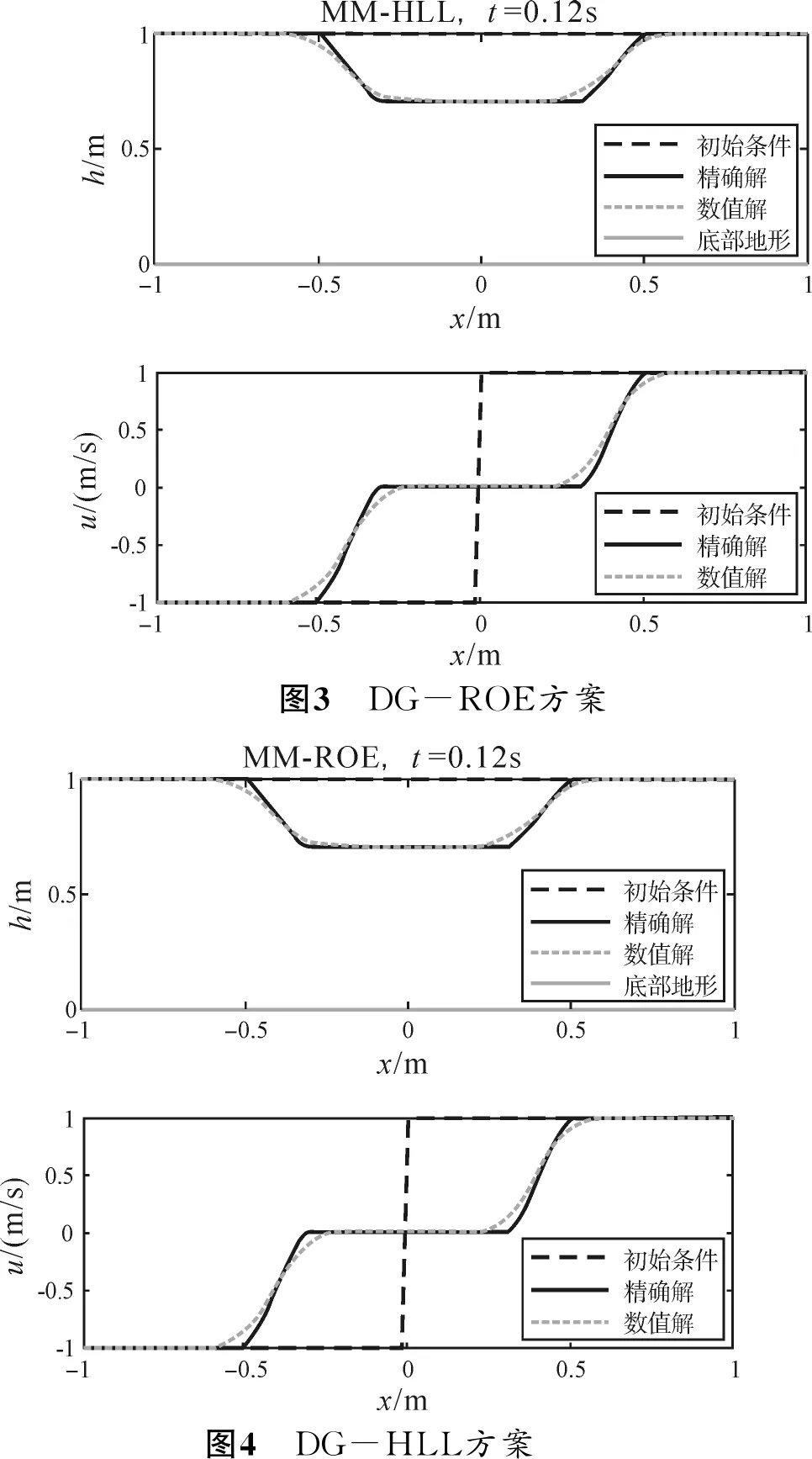
可以看出,使用改进的梯度限制器计算出了水深h与水流速度u分别在DG—LF,DG—RUS, DG—ROE和DG—HLL方案下同一网格上的数值解(包含接触不连续).可以看出,由DG—RUS, DG—HLL和DG—ROE方案计算的结果略优于DG—LF方案.关于不连续的解,以上几种方案的计算效果类似.

4 结语
本文系统地研究和比较了DG方法的四种不同数值通量,并对一维浅水波方程进行了模拟,结果表明ROE通量和改进的梯度限制器可能是DG方法的较好选择.本文仅对线性三角形单元和一维平底浅水波方程进行了测试,扩展到非平底河床和高维浅水波方程的研究,以及与现有模型相结合,将是下一步的工作.
