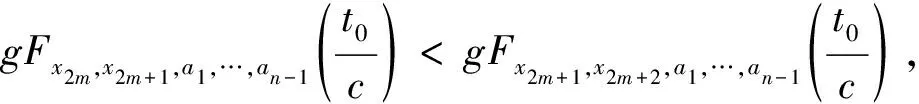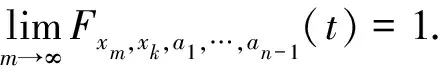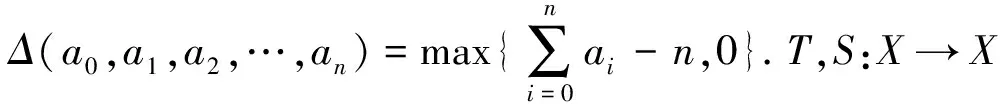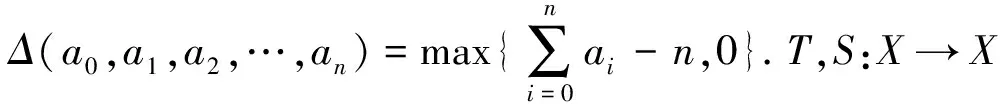非阿基米德Menger概率n-度量空间中一类映象的不动点定理
2020-08-25张树义
张树义,聂 辉
(渤海大学数理学院,辽宁 锦州 121013)
1 预备知识
关于在概率度量空间建立不动点定理文献[1-8]做过研究,其中文献[6]在概率n-度量空间中建立了一类映象的不动点定理.本文在非阿基米德Menger概率n-度量空间中建立一类新的映象对公共不动点的存在性定理,改进和推广了文献[1,7]中的相应结果.
定义1[1]映象f:=(-,+)→+=[0,+)称为分布函数,如果它是不减的、左连续的,
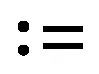
(ⅰ)Fp(0)=0;
(ⅱ)对任意n个相异的x1,x2,…,xn∈X,存在y∈X,t0>0,使得0≤Fp1(t0)<1,p1=(x0,x1,…,xn,y);
(ⅲ)Fp(t)=H(t)⟺p=(x0,x1,x2,…,xn)的坐标x0,x1,x2,…,xn中至少有两个相等;
(ⅳ)Fx0,x1,x2,…,xn=Fx1,x0,x2,…,xn=…=Fx1,x2,…,xn,x0;
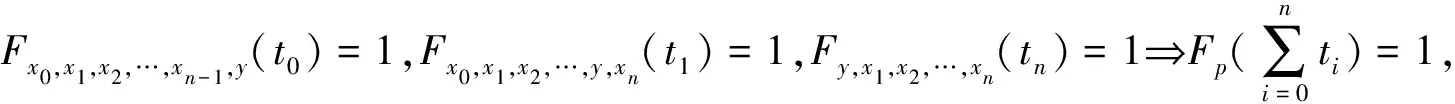
则称(X,F)为概率n-度量空间.
定义3[6]映象Δ:∏[0,1]→[0,1]称为三角范数(简称t-范数),如果满足以下条件:
(ⅰ)Δ(0,0,…,0)=0;∀a∈[0,1],Δ(a,1,1,…,1)=a;
(ⅱ)Δ(a0,a1,a2,…,an)=Δ(a1,a0,a2,…,an)=…=Δ(a1,a2,…,an,a0);
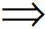
(ⅳ)Δ(Δ(a0,a1,a2,…,an),b1,b2,…,bn)=(Δ(a0,Δ(a1,a2,…,an,b1),b2,…,bn)=…=Δ(a0,a1,a2,…,an-1,Δ(an,b1,b2,…,bn)).
注1几种常用三角范数:∀ai∈[0,1],i=0,1,2,…,n.
2)Δ2(a0,a1,a2,…,an)=a0·a1·a2·…·an;
3)Δ3(a0,a1,a2,…,an)=min{a0,a1,a2,…,an}.
定义4[6]如果(X,F)是概率n-度量空间,Δ是t-范数且满足广义Menger三角不等式:

∀p=(x0,x1,x2,…,xn)∈∏X,∀y∈X,∀ti∈+,i=0,1,2,…,n,则称(X,F,Δ)为Menger概率n-度量空间.

(Ⅰ)若对∀ε>0,存在M=M(ε),当m≥M时,有Fxm,x,a1,…,an-1(ε)=1,∀ai∈X,i=1,2,…,n-1,则称序列{xm}收敛于x∈X.
(Ⅱ)若对∀ε>0,存在M=M(ε),当m,k≥M时,有Fxm,xk,a1,…,an-1(ε)=1,∀ai∈X,i=1,2,…,n-1,则称序列{xm}为Cauchy序列.
(Ⅲ)若X中任一Cauchy序列都收敛于X中的一点,则称(X,F)是完备的.
定义6如果定义2中条件(ⅴ)换为:
(ⅵ)∀y∈X,若Fx0,x1,x2,…,xn-1,y(t0)=1,Fx0,x1,x2,…,y,xn(t1)=1,…,Fy,x1,x2,…,xn(tn)=1,则Fp(max{t0,t1,…,tn})=1,∀p=(x0,x1,x2,…,xn)∈∏X,∀y∈X,∀ti∈+,i=0,1,2,…,n,
则称(X,F,Δ)为非阿基米德概率n-度量空间.
定义7称(X,F,Δ)为非阿基米德Menger概率n-度量空间,若(X,F)是一非阿基米德概率n-度量空间,Δ是满足下列条件的t-范数:
(ⅶ)Fp(max{t0,t1,…,tn})≥Δ(Fy,x1,x2,…,xn(t0),Fx0,y,x2,…,xn(t1),…,Fx0,x1,x2,…,xn-1,y(tn)),∀p=(x0,x1,x2,…,xn)∈∏X,∀y∈X,∀ti∈+,i=0,1,2,…,n.
设Ω={g|g:[0,1]→[0,)连续、严格递减,g(1)=0,g(0)<+}.
定义8非阿基米德Menger概率n-度量空间(X,F,Δ)称为(C)g型的,如果存在g∈Ω,使得∀p=(x0,x1,x2,…,xn)∈∏X,y,z∈X,∀t≥0,有
gFx0,x1,x2,…,xn-1,y(t)≤gFx0,x1,x2,…,xn-1,z(t)+gFx0,x1,x2,…,xn-2,z,y(t)+…+gFz,x1,x2,…,xn-2,y(t).

定义10设(X,F,Δ)是(C)g型非阿基米德Menger概率n-度量空间,(X,F,Δ)中序列{xm}收敛于x当且仅当对∀ε>0,λ>0,存在N(ε,λ)∈*,使得m≥N(ε,λ),有gFxm,x,a1,…,an-1(ε) 定义11设(X,F,Δ)是(C)g型非阿基米德Menger概率n-度量空间,(X,F,Δ)中序列{xm}称为Cauchy序列当且仅当对∀ε>0,λ>0,存在N(ε,λ)∈*,使得∀k,m≥N(ε,λ),有gFxk,xm,a1,…,an-1(ε) 引理1(ⅰ)如果非阿基米德Menger概率n-度量空间(X,F,Δ)是(D)g型的,则(X,F,Δ)是(C)g型的. 证明:(ⅰ)显然,下证(ⅱ).取g(t)=1-t,t∈[0,1],则g∈Ω,且 因此(X,F,Δ)是(D)g型的.证毕. 设∀t>0,∀ai∈X,i=1,2,…,n-1,0 注2取Φ(t)=βt,∀t∈+,0<β<1,则Φ∈Φ1. 证明:由引理2条件有 (1) 其中,Φm(t)表示Φ(t)的n次迭代函数.下证gFx0,x1,xs,a2,…,an-1(t)=0,s=0,1,2,….事实上,当s=0,1时gFx0,x1,xs,a2,…,an-1(t)=0显然成立.设gFx0,x1,xs,a2,…,an-1(t)=0对s≤k-1成立,现证对k也成立.由式(1)可推得 gFx0,x1,xk,a2…,an-1(t)≤gFxk-1,x1,xk,a2,…,an-1(t)+gFx0,xk-1,xk,a2,…,an-1(t)+ …+gFx0,x1,xk,a2,…,xk-1,an-1(t)+gFx0,x1,xk,a2,…,an-2,xk-1(t)≤ 定理1设(X,F,Δ)是(C)g型非阿基米德Menger概率n-度量空间.T,S:X→X是两映象,对∀x,y∈X,t>0,有 (2) 其中Φ∈Φ1,∀ai∈X,i=1,2,…,n-1,0 证明:对x0∈X,可归纳定义序列{xm}为x2m+1=Tx2m,x2m+2=Sx2m+1,m=0,1,2…,注意到如果对某个m,xm=xm+1,则xm是T与S在X上一公共不动点.事实上,如果对某个m,x2m=x2m+1,则x2m是T不动点.由式(2)有 gFx2m+2,x2m+1,a1,…,an-1(t)=gFSx2m+1,Tx2m,a1,…,an-1(t)≤ 于是gFx2m+1,x2m+2,a1,…,an-1(t)=0,即x2m+1=x2m+2.因此,x2m是T与S在X上一公共不动点.如果对某个m,x2m+1=x2m+2,则类似如上证明,由式(2)可得x2m+1是T与S在X上一公共不动点.假设对任意m≥0,xm≠xm+1,由式(2),对∀t>0,有 gFx2m+2,x2m+1,a1,…,an-1(t)=gFSx2m+1,Tx2m,a1,…,an-1(t)≤ (3) 在式(3)中取a1=x2m,有 因此,gFx2m+1,x2m+2,x2m,a2,…,an-1(t)=0.由式(3),对∀t>0,有 (4) 同理对∀t>0,有 于是对m=0,1,2,…,∀t>0,有 连续重复上述步骤m次,有 (5) 下证{xm}是Cauchy序列.对∀k,m∈:k>m,注意到Φ∈Φ1,g∈Ω,由式(5)和引理2有 Fxm,xk,a1,…,an-1(t)≥Δ(Fxm+1,xk,a1,…,an-1(ct),(Fxm,xm+1,a1,…,an-1(t),Fxm,xk,xm+1,a2,…,an-1(t),…,Fxm,xk,a1,…,an-2,xm+1(t)))≥ Δ(Δ(Fxm+2,xk,a1,…,an-1(c2t),Fxm+1,xm+2,a1,…,an-1(ct),Fxm+1,xk,xm+2,a2,…,an-1(ct),…,Fxm+1,xk,a1,…,an-2,xm+2(ct)), (Fxm,xm+1,a1,…,an-1(t),Fxm,xk,xm+1,a2,…,an-1(t),…,Fxm,xk,a1,…,an-2,xm+1(t)))= 从而gFz,Sz,a1,…,an-1(t)=0,于是z=Sz.故z是T与S在X上的一公共不动点.类似地,若S连续,则T与S在X上有一公共不动点.假设T与S在X上还有另一公共不动点w.由式(2)有 因此z=w.证毕. 如果(X,F,Δ)是非阿基米德Menger概率n-度量空间,取 则由引理1知(X,F,Δ)是(D)g型非阿基米德Menger概率n-度量空间,其中g(t)=1-t,t∈[0,1].于是由定理1有: 其中Φ∈Φ1,∀ai∈X,i=1,2,…,n-1,0 在定理2取Φ(t)=βt,∀t∈+,0<β<1,则有: 其中∀ai∈X,i=1,2,…,n-1,0 注3可把本文结果推广到积分型四个映象的情形.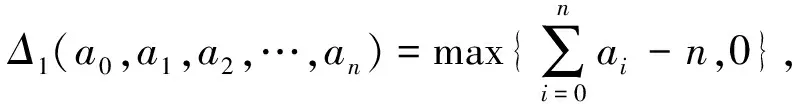

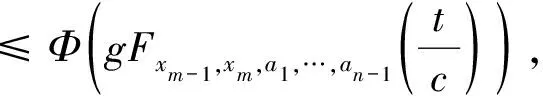

2 主要结果