基于随机投影的高维数据流聚类

朱颖雯 陈松灿

1(南京航空航天大学计算机科学与技术学院 南京 211106)2(模式分析与机器智能工业和信息化部重点实验室(南京航空航天大学) 南京 211106)3(三江学院计算机科学与工程学院 南京 210012)(yingwen.zhu@nuaa.edu.cn)

随着云计算、物联网的快速发展，许多新型的应用领域，诸如网络入侵检测、视频监控、气象卫星遥感以及电力供应网等，每时每刻都在产生大量的数据.这些数据并不事先存放在存储介质中，而是像水流一样不断出现，它们具有快速(high speed)、时序(temporally ordered)、海量(massive)等特征，被称作数据流(data stream).

越来越多数据流的产生和应用需求使得对于数据流的挖掘变得炙手可热.挖掘数据流[1-9]的目的是从这些连续不断的流数据中提取隐藏的知识结构.数据流挖掘技术包括数据流分类、数据流聚类、数据流关联规则挖掘等.其中，数据流聚类是数据流学习的一项重点任务，它是将数据对象集合中相似对象划分为一个或多个组(称为“簇”，cluster)的过程，划分后同一簇中元素彼此相似，但与其他簇中元素相异.不同于传统的静态数据聚类，数据流聚类面临许多问题，例如：1)有限内存(bounded memory)，数据流中的数据常是海量，所以不可能在内存及硬盘上存储整个数据流集；2)一次扫描(single-pass)，同样因为数据量巨大，传统的多遍扫描方法不再适用，对其挖掘应该是一个单遍扫描过程，且对流中数据元素的访问只能单次线性(linear scan)，即只能按照流入顺序依次读取一次，无法进行随机访问；3)实时响应(real-time response)，多数应用要求快速响应，因此挖掘应该是一个连续在线的过程；4)概念漂移(concept-drift detection)，数据分布常随着时间的推移而发生变化.

目前，对于数据流聚类算法的研究已在学术界和工业界得到了广泛关注，许多相关算法已被提出[10-26].现有数据流聚类算法均由传统聚类算法扩展而来，根据其所扩展的传统算法不同，我们可以将其分为5类：基于划分的方法(STREAM[10])；基于层次的方法(CluStream[11],HPStream[12],SWClustering[13],E-Stream[14],REPSTREAM[15])；基于密度的方法(DenStream[16],ACSC[17],OPTICS-Stream[18],incPre-Decon[19])；基于网格的方法(D-Stream[20],MR-Stream[21],CellTree[22])；基于模型的方法(SWEM[23],GCPSOM[24],G-Stream[25],RPGStream[26]).表1分别针对6个特性对现有方法进行总结：1)基算法；2)所用计算策略(在线学习或两步学习)；3)类簇个数是否自适应；4)是否可挖掘拓扑结构；5)是否可检测概念漂移；6)是否适合高维数据.

如表1所示，基于划分的数据流聚类方法相对简单并易于实现，但其需要预先定义类簇个数，然而由于数据分布未知，类簇个数通常无法直接得到.此外，该方法无法检测概念漂移.基于层次的数据流聚类方法虽然能够发现有意义的类簇结构，但其一般具有较高的计算代价，而且对流数据到达的顺序敏感.基于密度的数据流聚类方法可以发现任意形状的类簇，但是算法需要预设较多参数.基于网格的数据流聚类方法运行速度较快，也可以发现任意形状的类簇，但是其聚类质量取决于选取的网格粒度.基于模型的数据流聚类方法包含了很多领域知识并强依赖于假设模型，例如SWEM算法基于EM模型、GCPSOM算法基于SOM模型、G-Stream和RPG-Stream算法均基于GNG模型.从表1我们发现，在线(联机)学习算法是处理数据流聚类的一个很好策略，可以解决数据流约束中的一次扫描，实时响应和有限内存问题.STREAM[10]，REPSTREAM[15]，ACSC[17]，incPre-Decon[19]，SWEM[23]，GCPSOM[24]，G-Stream[25]和RPGStream[26]均为在线学习算法，但只有REPSTREAM，ACSC，SWEM，GCPSOM，G-Stream和RPGStream可以处理概念漂移，即此算法能够随着数据的流动更新新来的概念并移除旧的概念.GCPSOM,G-Stream和RPGStream不仅可以解决数据流挖掘中的各类约束，同时可以发现数据的拓扑结构，它们分别基于SOM(self-organizing maps)和GNG(growing neural gas)模型.但GCPSOM和G -Stream面对高维数据无能为力，据现有资料显示只有HPStream[12],incPre -Decon[19]和RPGStream[26]可以处理高维数据.RPGStream虽然可以处理高维数据，但因其基于GNG模型，超参数较多，调节参数对算法性能影响较大.故本文的直接动机是设计一个可在单机执行、适用于高维数据流的高效数据流聚类算法.

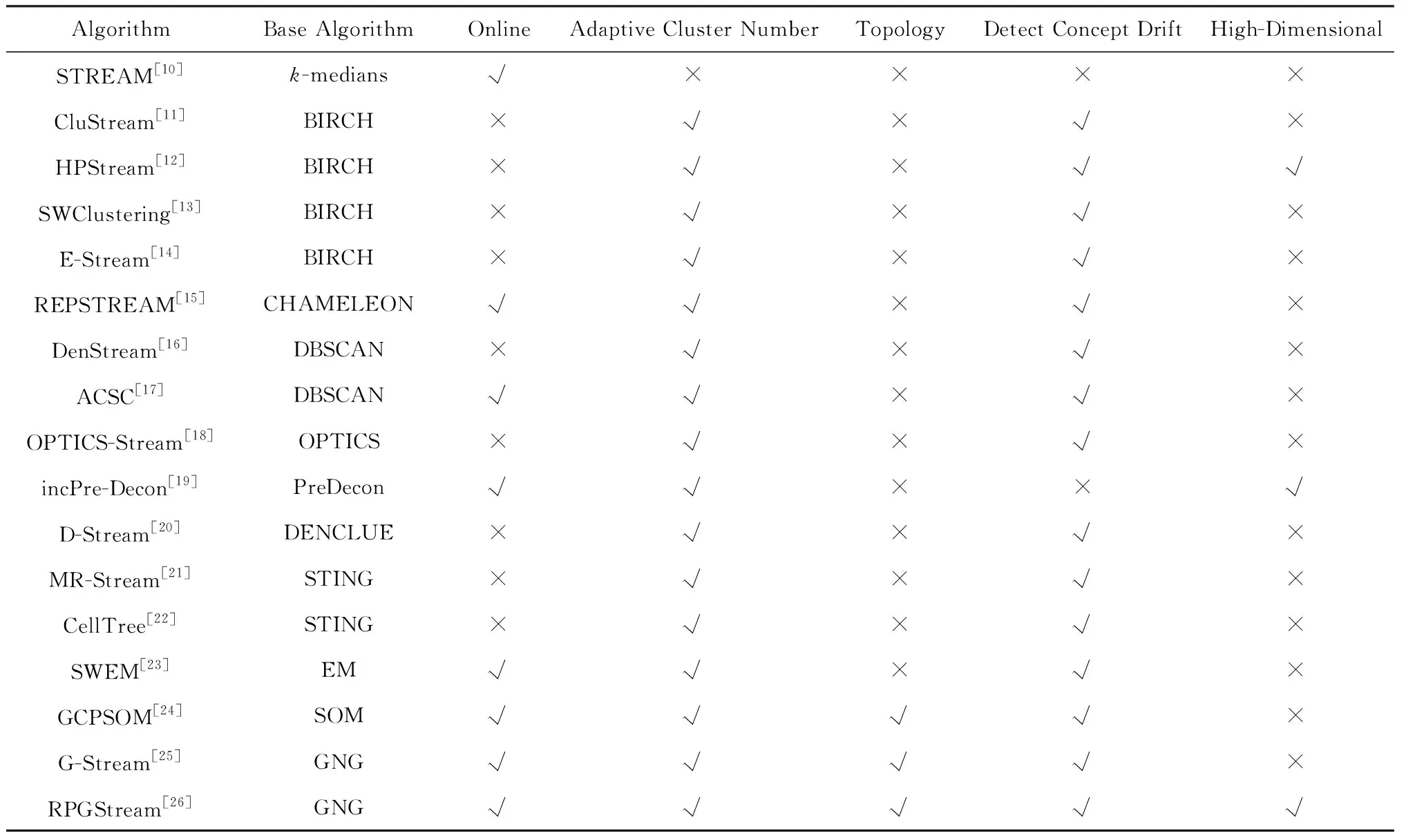
Table 1 Comparison of Various Data Stream Clustering Algorithms表1 数据流聚类算法比较

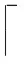
为解决高维数据流聚类问题(n和d均很大)，本文提出了一种基于随机投影的高维数据流聚类算法RPFART.首先通过随机投影将原始高维数据映射到低维数据空间，再使用ART模型[42]进行数据流聚类.ART具有线性计算复杂度，且仅使用1个超参数，并对参数设置鲁棒.虽然将随机投影用于K-Means算法可以分析理论最差界，但由于ART本身的复杂性我们无法分析RPFART的最差界.所以，本文中我们使用大量实验分析RPFART算法的聚类性能.多个数据集上的实验结果表明:即使原始尺寸压缩到10%，RPFART算法仍可以达到与RPGStream算法相当甚至更好的性能.对于ACT1数据集，其维数从67 500减少到6 750.

1 相关工作

1.1 数据流聚类与ART

自组织神经网络是人工智能领域应用最为广泛的一种学习模型.为解决大部分神经网络模型遭遇的“稳定性-弹性问题”，美国Boston大学的Grossberg和Carpenter于1976年提出了一种无监督竞争型神经网络模型，即自适应谐振理论网络(adaptive resonance theory, ART)[43]，可在稳定原有模式类的前提下学习新的模式.ART模拟了人类大脑如何捕捉、识别、记忆关于事物和事件的信息.随着理论的不断完善，学者们提出了大量基于ART改进的无监督学习模型，如ART1[44],ART2[45],ART2-A[46],ART3[47]和模糊ART(fuzzy ART)[42].模糊ART通过在类别空间实时搜索和匹配现有类簇，增长式地逐步处理每一个输入模式，是本文研究的基本模型.警戒参数(vigilance parameter)用于约束在同一个类簇中模式的最小相似度.当输入模式与现有类簇都不相似时，则生成一个新的类簇来编码这个新模式.模糊ART已用于解决图像和文本挖掘问题，如Web文档管理、基于标记的Web图像组织、图像-文本关联，但还未用于数据流聚类.

模糊ART模型由输入层F1和识别层F2组成，如图1所示.输入层F1包含的输入向量I被提交到网络，与识别层F2中各个类簇的权值向量进行相似度比较并归类.

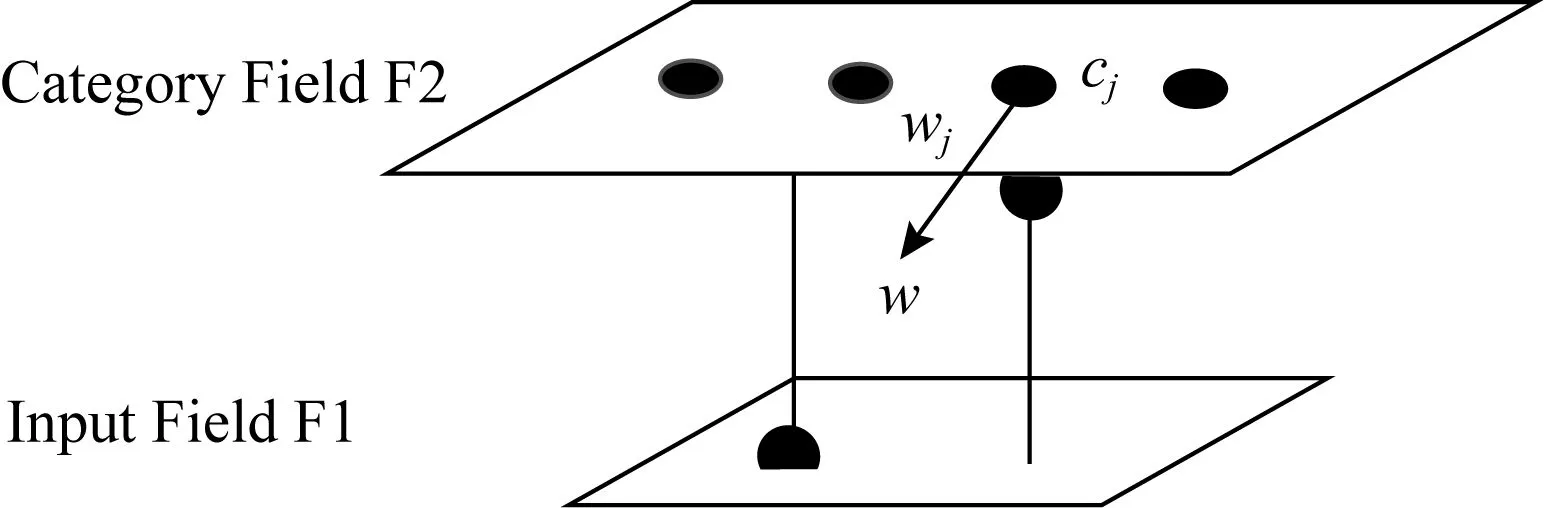
Fig.1 Fuzzy ART architecture图1 模糊ART结构

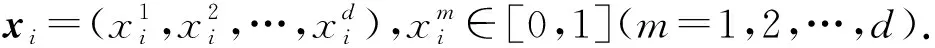
2) 权值向量(weight vector).设wj表示识别层F2中第j个类cj(j=1,2,…,J)的权值.

3) 参数(parameter).模糊ART随着3个参数动态改变，它们分别是选择参数α>0、学习参数β∈[0,1]、以及警戒参数ρ∈[0,1].

模糊ART聚类过程包含3个关键步骤：

步骤1. 类别选择(category choice).对每个输入模式I，模糊ART根据选择函数计算此输入对识别层F2中的每个类簇的选择值，并取具有最大值的类簇作为获胜类簇cj*.第j个类簇cj的选择函数定义为

(1)

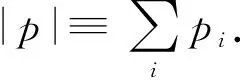
步骤2. 模板匹配(template matching).输入模式I与获胜类簇cj*使用匹配函数Mj*进行评估，Mj*定义为

(2)

如果获胜类簇cj*的Mj*≥ρ，则发生共振(resonance)，引发步骤3——中心学习.否则，返回步骤2，继续在剩下的类簇中寻找一个获胜类簇.如果所有选出的获胜类簇均不满足Mj*≥ρ，则生成一个新的类簇来编码这个输入模式I.

步骤3. 中心学习(prototype learning).如果获胜类簇cj*的Mj*≥ρ，根据式(3)更新其权值向量wj*.

(3)

1.2 随机投影

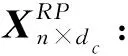
(4)

随机投影的理论依据是JL引理[31]：高维欧氏空间里的点集映射到低维空间，其相对距离得到一定误差范围内的保持.

(5)

这里参数ε控制距离保持的精度，β控制投影成功的概率.dc是一个正整数，且dc≥k0，随机矩阵R是一个d×dc矩阵，R(i,j)=rij,rij是一个独立的随机变量，可以由3种概率分布生成：

rij～N(0,1);

(6)

(7)

(8)

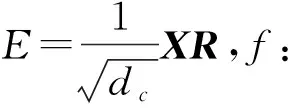
对所有的u,v∈X，在至少1-n-β概率下:

(9)

从式(9)可以看出，理论上JL界(k0)不依赖于原始空间的维度d，为了得到定理1的结果，我们只需要通过一个简单的概率分布生成随机矩阵R，同时进行投影计算.

通过假设输入数据的期望为0，在主成分分析的激励下，文献[41]给出结论：根据概率上的方差分析，压缩后的数据获得了原始数据的全部可变性.首先，压缩后的数据可以从低维数据中获得很多信息，因为这些低维都是线性无关的.其次，原始数据维度的方差之和等于投影后数据维度的方差之和.

1) 投影数据的维度是相互独立的.

Cov(Yi,Yj)=0,∀i≠j;

2) 随机投影保持了可变性.

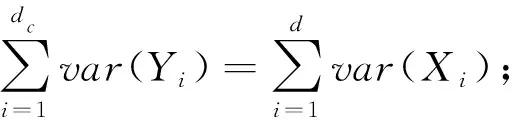
利用上述性质，已有相关工作验证了将随机投影应用于聚类问题的可行性.Boutsidis等人[33]首次将随机投影与k-Means结合进行聚类;吴等人[34]和Schneider等人[37]针对SLC和ALC聚类以及最小生成树(MST)问题，探索了基于随机投影的快速层次聚类算法.同时Schneider和Vlachos[38]通过使用随机投影来扩展基于密度的聚类，并提出了显著提高学习效率的算法.Ferns和Brodley[39]、Cardoso和Wichert[40]、叶等人[41]提出了使用随机投影对高维数据聚类的集成模型和迭代模型.

2 基于随机投影的数据流聚类算法

2.1 RPFART算法

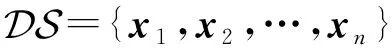
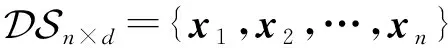
算法1.RPFART算法.

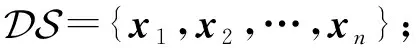
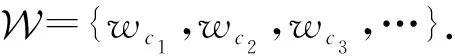
① 生成满足定理1的随机矩阵Rd×dc(dc≪d);

② for eachxi

③yi=xi×R；

④ 对yi使用模糊ART算法进行聚类；

⑤ end for

2.2 算法复杂度分析

算法1中最耗时的运算是步骤③和步骤④.可以看出随机投影在计算上非常简单，可以快速生成，故步骤③的投影时间复杂度为O(nddc).模糊ART算法包含了类别选择、模板匹配、中心学习3个主要步骤，每个步骤的时间复杂度分别为O(d)，O(md)，O(d)，给定n个输入样本，总体时间复杂度为O(nmd)，其中m是聚类结果中节点个数.故步骤④的时间复杂度为O(nmdc).RPFART算法的总体时间复杂度为O(nddc+nmdc).

3 实验与结果

为了验证本文提出算法的有效性，我们在5个数据集上与现有数据流聚类算法RPGStream进行了比较.实验使用的计算机配置为Intel Core i5-6300U 2.4 GHz处理器和8 GB内存，Windows 10操作系统，所有比较程序均在MATLAB R2015a上设计和运行.

3.1 聚类评价指标

为了对各种聚类算法性能进行评价，我们引入了3项评价指标[26]：1)accuracy(purity);2)NMI(normalized mutual information);3)RI(rand index).

1) Accuracy(Purity)

(10)

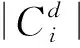
2)NMI(normalized mutual information)

归一化互信息NMI是一个量化2个分布之间共享统计信息的对称策略.当类簇标签和真实样本类别一对一映射时NMI值到达最大值1.0.给定真实类簇A={A1,A2,…,Ak}和某聚类算法得到的类簇B={B1,B2,…,Bh}，混淆矩阵C中的元素Cij表示即在Ai又在Bj中的样本个数.NMI计算为

NMI(A,B)=

(11)

其中，CA(CB)表示A(B)中样本个数,Ci.(C.j)表示C中i行元素和(C中j列元素和)，N表示样本个数.

3)RI(rand index)

RI比较n×(n-1)/2个数据对，其中n为数据集中样本个数，P1，P2为2种聚类算法，n11为数据对(xi,xj)在P1，P2中划分为同一类的数据对数，n00则为(xi,xj)隶属不同类的数据对数，RI错误率计算为

(12)

由式(12)可得RI∈[0,1]，当P1与P2划分完全一致时RI=1.

3.2 数据集和参数设置

为了对RPFART算法的聚类有效性进行评价，实验中我们使用了人工和真实数据集，表2给出数据集的相关信息：

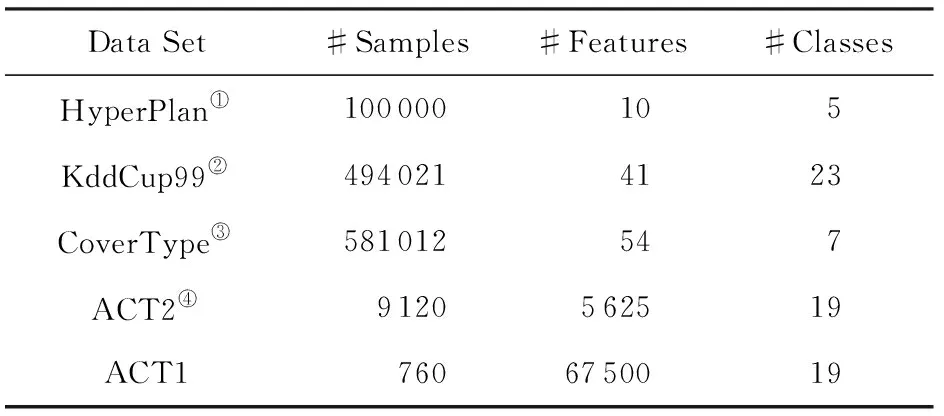
Table 2 Statistics of Five Datasets表2 数据集

HyperPlan数据集是人工模拟数据集.HyperPlan是一个含有概念漂移的数据流，包含5个类共10万个样本，每个样本5维.KddCup99，CoverType和ACT均来自UCI.KddCup99数据集最早来源于MIT林肯实验室的一项入侵检测评估项目,记录了9周内TCP网络连接和系统审计数据,仿真各种不同的用户类型、网络流量和攻击手段.这些原始数据包含约50万条连接记录的训练集.每个连接记录包含41个属性，这些连接记录含1种正常的标识类型和22种训练攻击类型共23个类别.CoverType数据集来源于US Geological Survey (USGS)和US Forest Service (USFS)对位于Roosevelt国家森林的四片荒野区域的观测.数据集中包含581 012条记录,这些记录最终被分为7种类型.每条观测记录包含54个地质学和地理学属性.ACT(The Daily and Sports Activities Data Set)数据集包含45个传感器在5 min内以25 Hz的采样频率收集的19项活动的数据.为了获得高维数据集，我们分别将1 min和5 s的活动数据处理为一个样本，结果得到了760×67 500(ACT1)和9 120×5 625(ACT2)数据矩阵.

由算法1所示，RPFART算法需要设置警戒参数ρ和压缩率r.RPGStream算法设置εb=0.01、εn=0.001、β=300(ACT1取30)、λ1=0.2、λ2=0.2、|windows|=600(ACT1取60)、|reservoir|=400(ACT1取50)、agemax=250(代表边年龄的最大值)、weightmin=2(代表神经元节点权值的最小值)，并且每次插入新节点的个数NbNodesInserted=3.

3.3 聚类性能比较

首先评估RPFART的聚类质量，并将其与RPGStream算法在5个数据集上进行比较.每个算法重复实验10次.聚类结果如表3～5所示.参数r表示压缩率，例如对于KddCup99数据集，r=90%表示通过随机投影将特征数减少到54×0.9=48.

从表3～5中我们可以发现：1)RPFART在使用了随机投影后，总体上与RPGStream的结果相当，特别是NMI和Rand指数在所有数据集上均超过了RPGStream.2)RPFART在HyperPlan和ACT2数据集上的聚类纯度略低于RPGStream.3)即使设置一个小的r，例如r=10%，RPFART在ACT1上的聚类纯度、NMI和Rand指数仍然是最好的.4)我们的算法不限于海量数据，即使对高维小样本也可以得到很好的结果，如在ACT1数据集上取得了较好的效果.

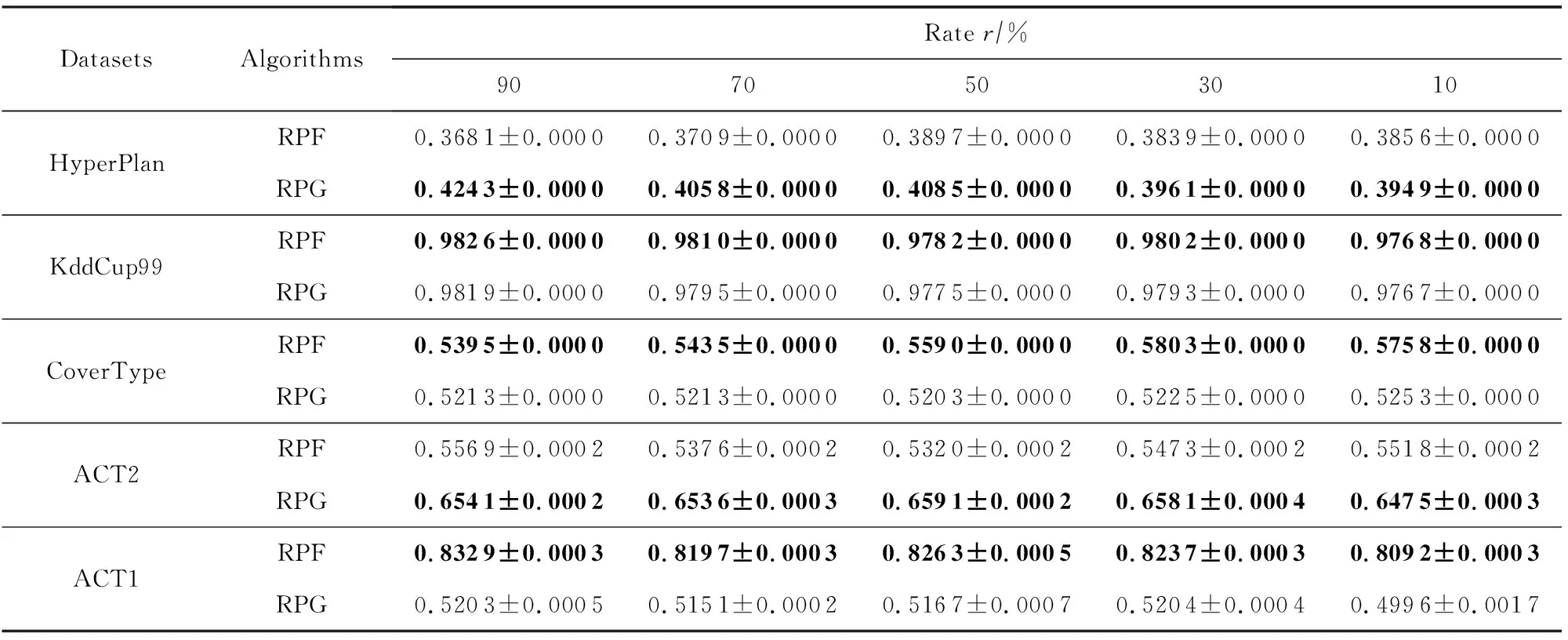
Table 3 The Comparison Results of RPFART and RPGStream in Terms of Accuracy表3 RPFART(RPF)和RPGStream(RPG)在不同数据集上的聚类性能Accuracy比较

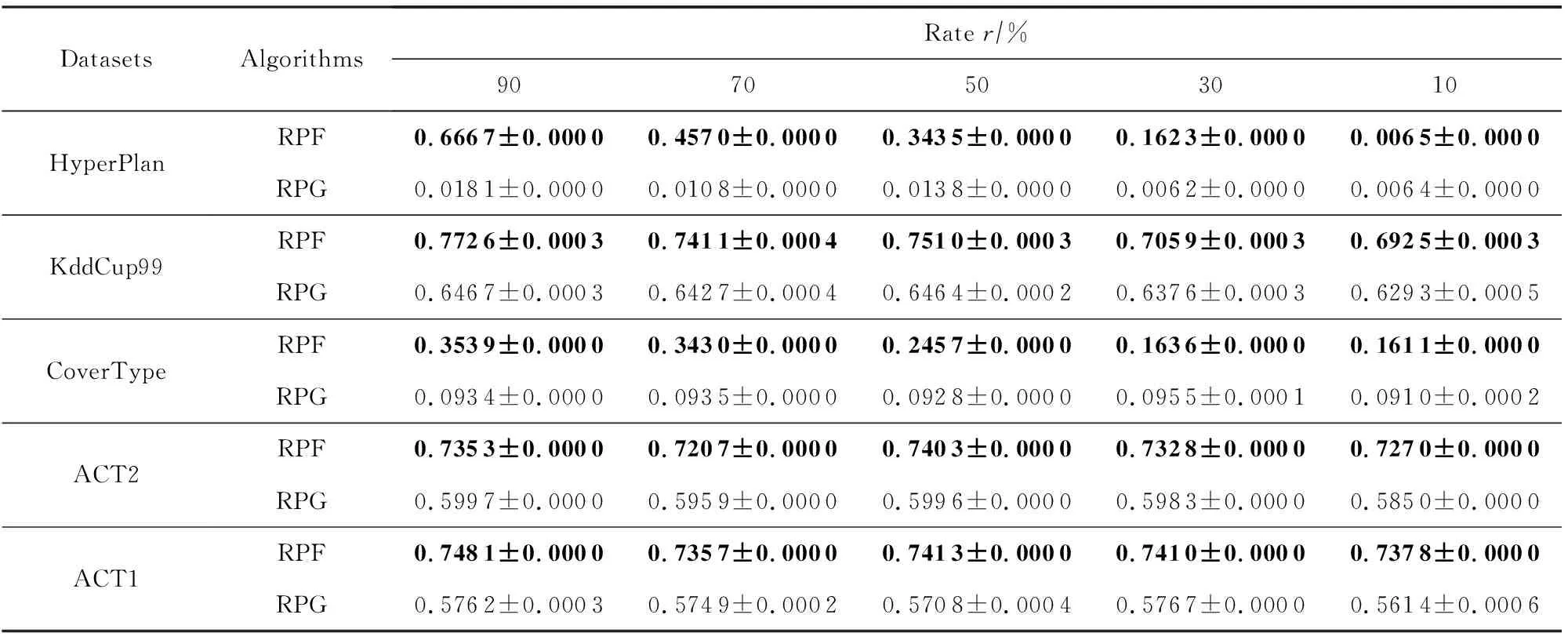
Table 4 The Comparison Results of RPFART and RPGStream in Terms of NMI表4 RPFART(RPF)和RPGStream(RPG)在不同数据集上的聚类性能NMI比较

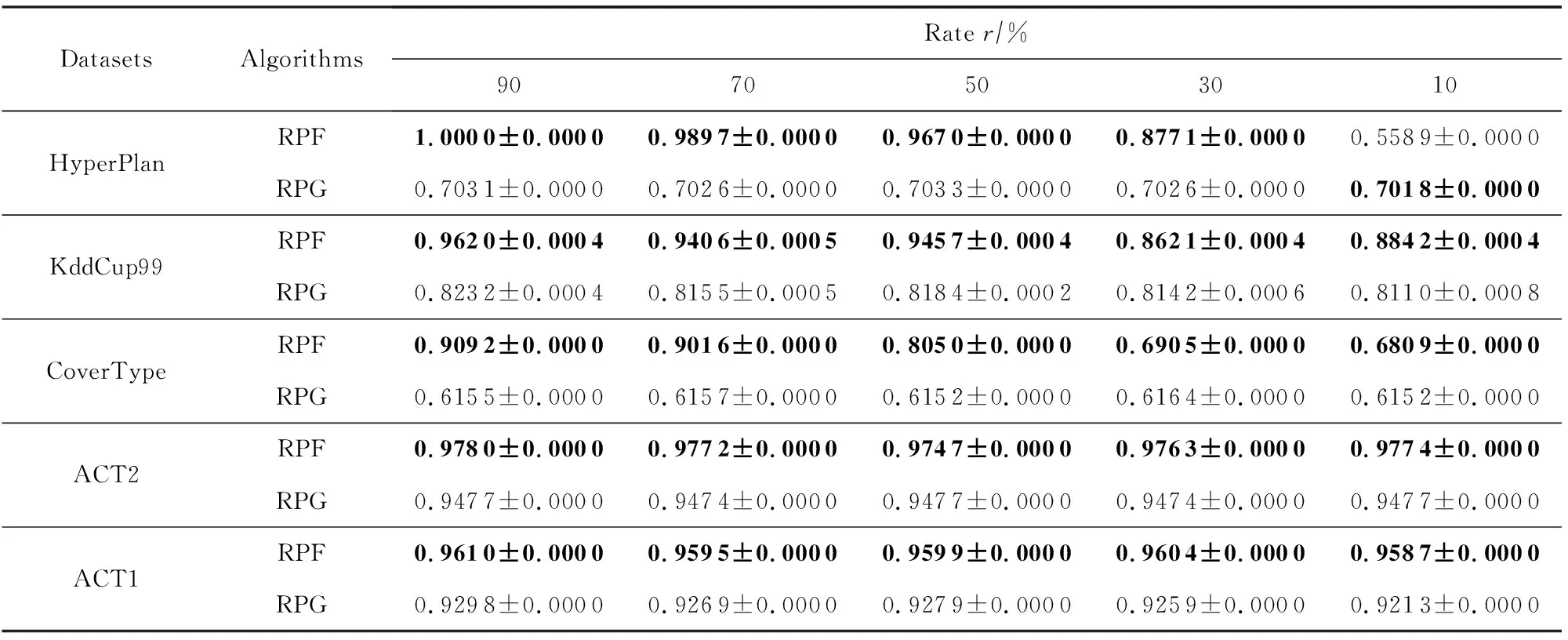
Table 5 The Comparison Results of RPFART and RPGStream in Terms of Rand Index表5 RPFART(RPF)和RPGStream(RPG)在不同数据集上的聚类性能RI比较

为了进一步证明RPFART的性能，我们分别在5个数据集上与离线聚类算法RPK-Means和PCAFART进行了比较.PCAFART算法是将模糊ART与PCA结合对数据流进行聚类.其结果如表6～8所示.

从表6～8中我们可以发现：1)RPFART在精度、NMI、Rand指数都优于KddCup99，CoverType，ACT2，ACT1数据集上的RPK-Means.2)RPFART与PCAFART具有相当的聚类结果，但后者在处理高维ACT1数据集时，出现内存耗尽溢出问题.因此，我们可以得出RPFART更适合于高维数据，同时结合随机投影和模糊ART是可行和有前途的.此外，RPFART的方差比其他方法略小，这表明它相对稳定.除了随机投影，PCA也可以用来降维，但当我们想将PCA与模糊ART结合用于ACT1数据集时，算法因为内存不足而停止.

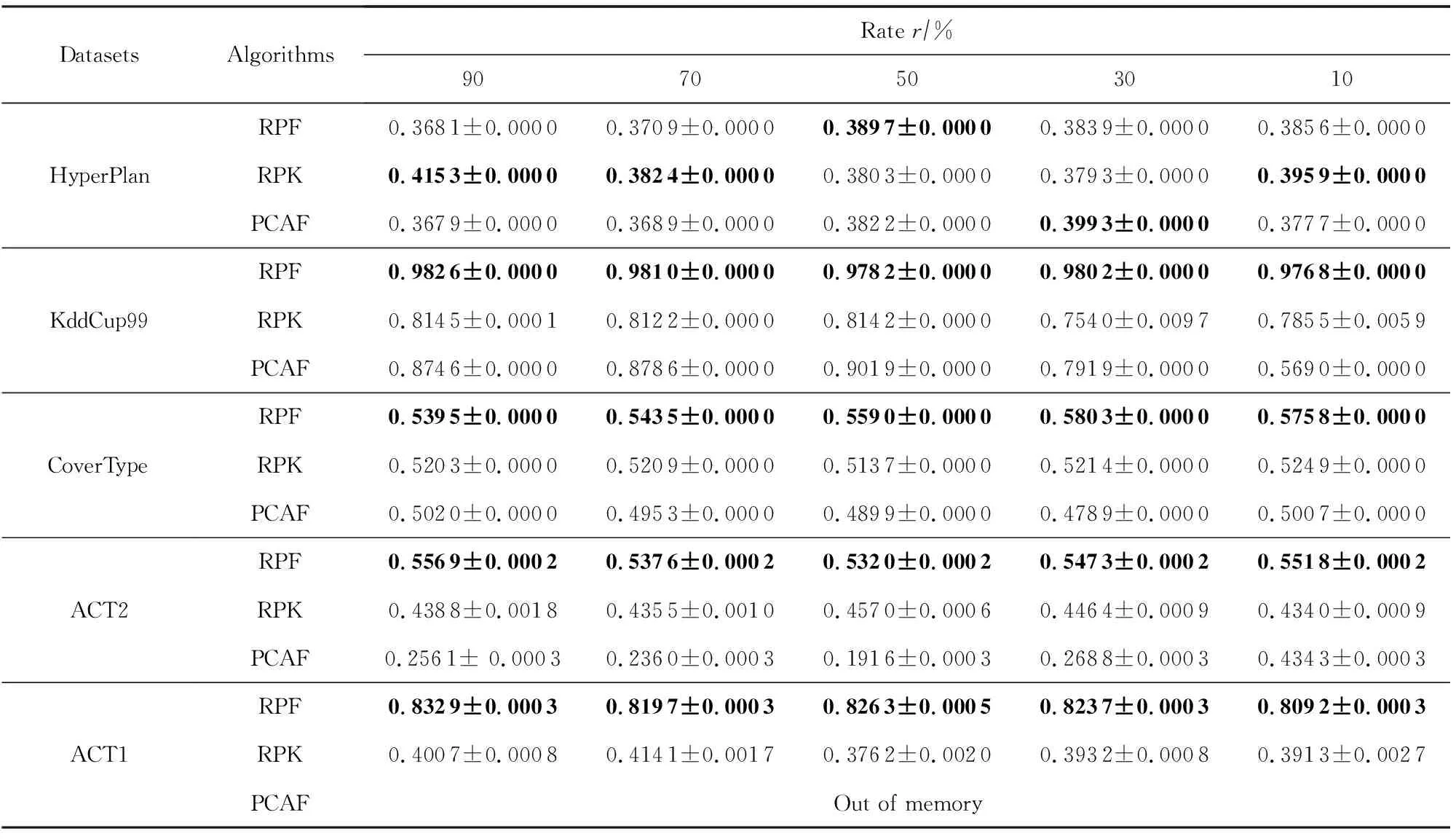
Table 6 The Comparison Results of RPFART, RPK-Means and PCAFART in Terms of Accuracy表6 RPFART(RPF)和RPK-Means(RPK), PCAFART(PCAF)在不同数据集上的聚类性能Accuracy比较

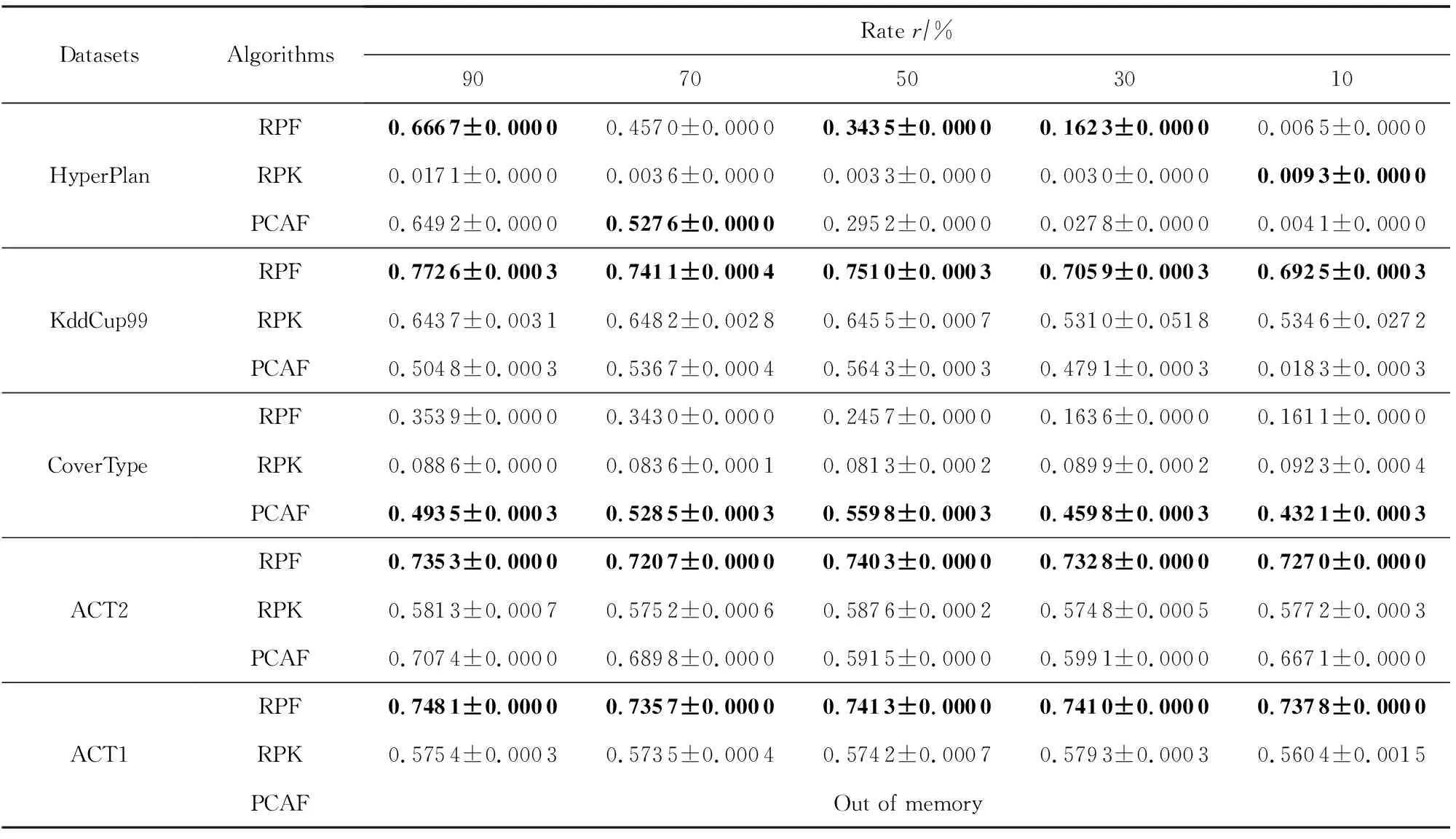
Table 7 The Comparison Results of RPFART, RPK-Means and PCAFART in Terms of NMI表7 RPFART(RPF)和RPK-Means(RPK), PCAFART(PCAF)在不同数据集上的聚类性能NMI比较

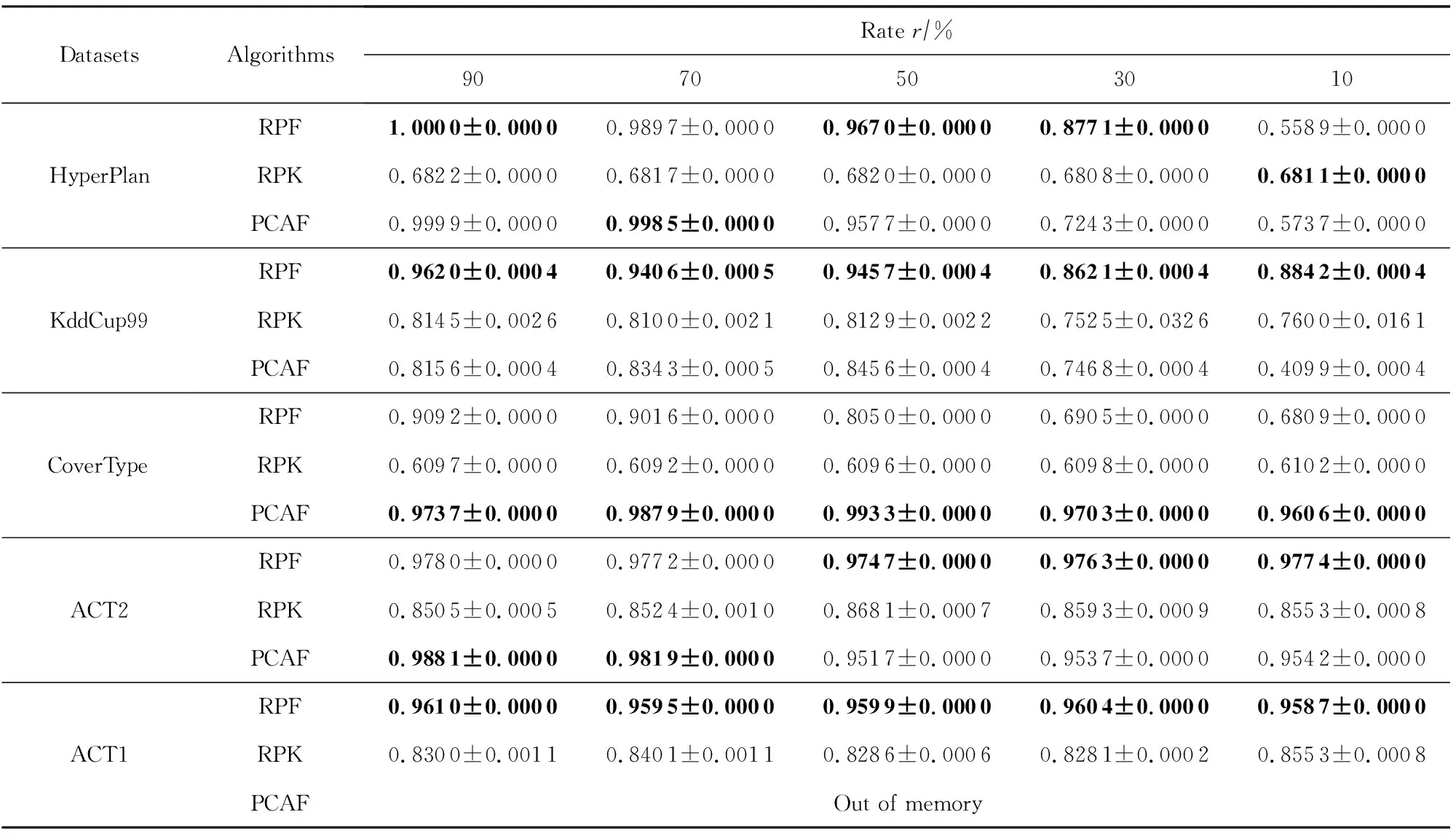
Table 8 The Comparison Results of RPFART, RPK-Means and PCAFART in Terms of RI表8 RPFART(RPF)和RPK-Means(RPK), PCAFART(PCAF)在不同数据集上的聚类性能RI比较

3.4 运行时间比较

图2显示了r=50%时的5个数据集上RPFART和RPGStream的运行时间.

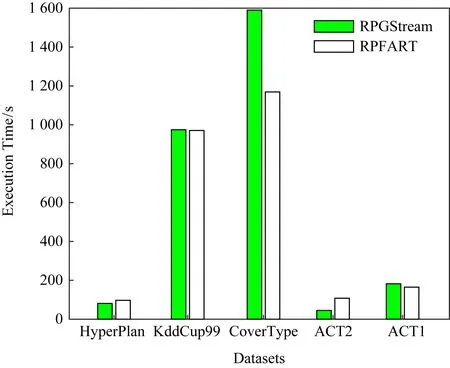
Fig. 2 Execution time(in seconds)图2 运行时间比较

从图2可以看出：1)RPFART和RPGStream的执行时间都随着数据量的增加而增加.2)随着样本数的增加RPFART比RPGStream更快.研究表明，RPFART算法对大规模、高维数据的处理效率更高.

3.5 随机矩阵的选择

由于RPFART是基于随机投影的，所以直观地说，随机矩阵R的类型选择将在一定程度上对聚类性能产生影响.因此，为分析其影响，我们使用不同类型的随机矩阵进行实验，典型的有高斯分布(式(6))、均匀分布(式(7))和稀疏分布(式(8))随机矩阵.我们还利用Gram Schmidt方法对上述随机矩阵进行正交实验.所有实验均在HyperPlan,Kddcup99,CoverType,ACT2上进行，重复10次，r=50%.结果如表9所示.结果表明，正交后RPFART算法在聚类纯度、NMI和Rand指数上比非正交算法较优.然而，正交化并不免费，计算上十分昂贵.有趣的是，Hecht-Nielsen[48]证明高维空间中存在大量几乎正交(而不是严格正交)的方向，即具有随机方向的一系列向量同样可以是有效正交，从而其可作为一组基的近似.

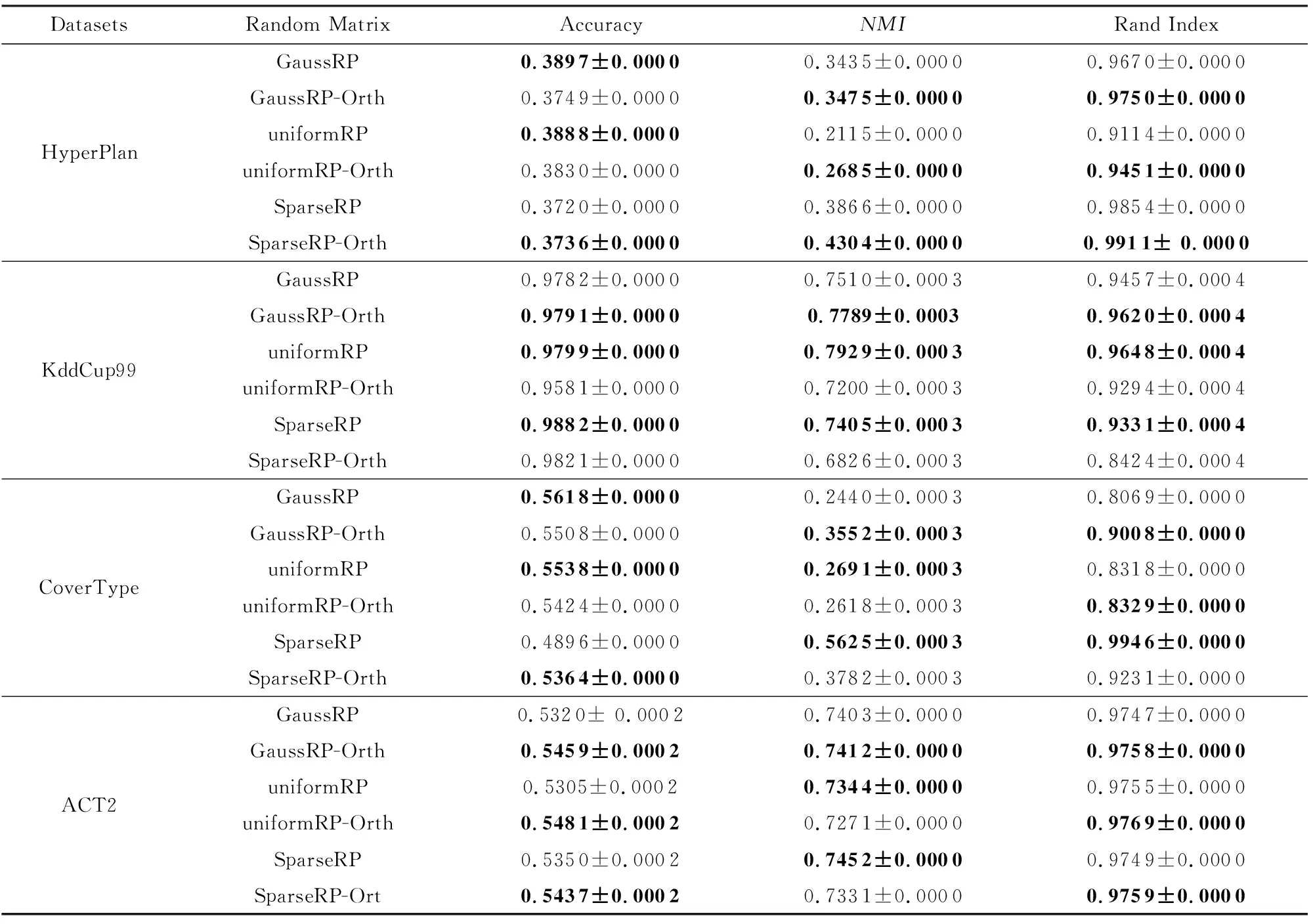
Table 9 Performance of Clustering Algorithms with Different Random Matrix表9 不同随机矩阵对RPFART的影响

3.6 处理非平稳数据能力

本节研究RPFART在非平稳数据流聚类中的有效性.许多实际应用程序中，数据通常随着时间演变，即具有非平稳性.例如，第1个类的数据点全部到达后，第2个、第3个类的数据点才依次按类别到达.这种情况下，旧的概念消失，同时新的概念随着新的数据点的到来而出现，从而导致概念漂移.因此我们分别将RPFART在类排序(按类标签)和类未排序的数据流上进行聚类，重复实验10次.图3～5显示了RPFART的聚类纯度、NMI和Rand指数.

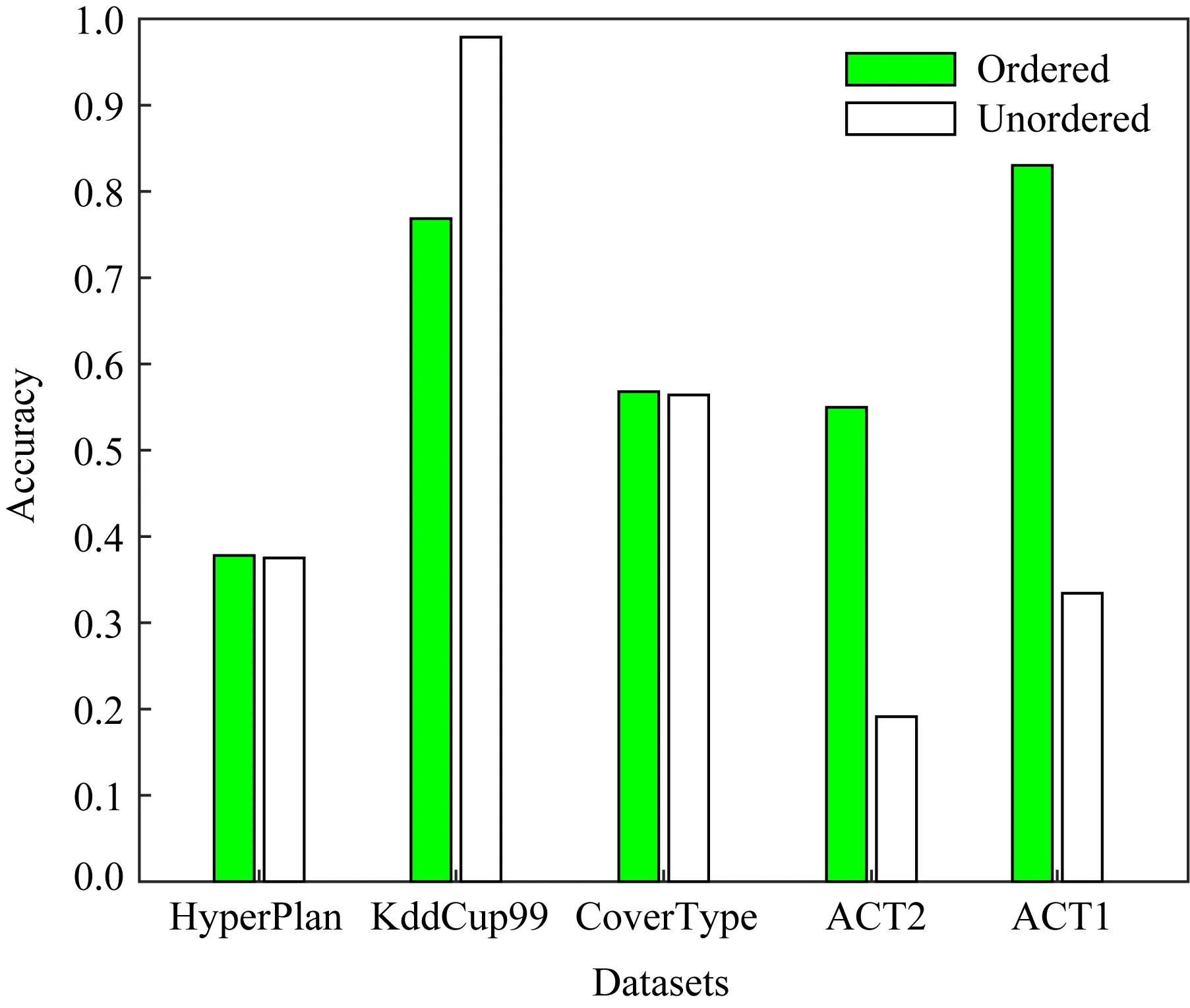
Fig. 3 Accuracy of RPFART with and without ordering of classes图3 RPFART在类排序与类未排序数据集上的聚类纯度

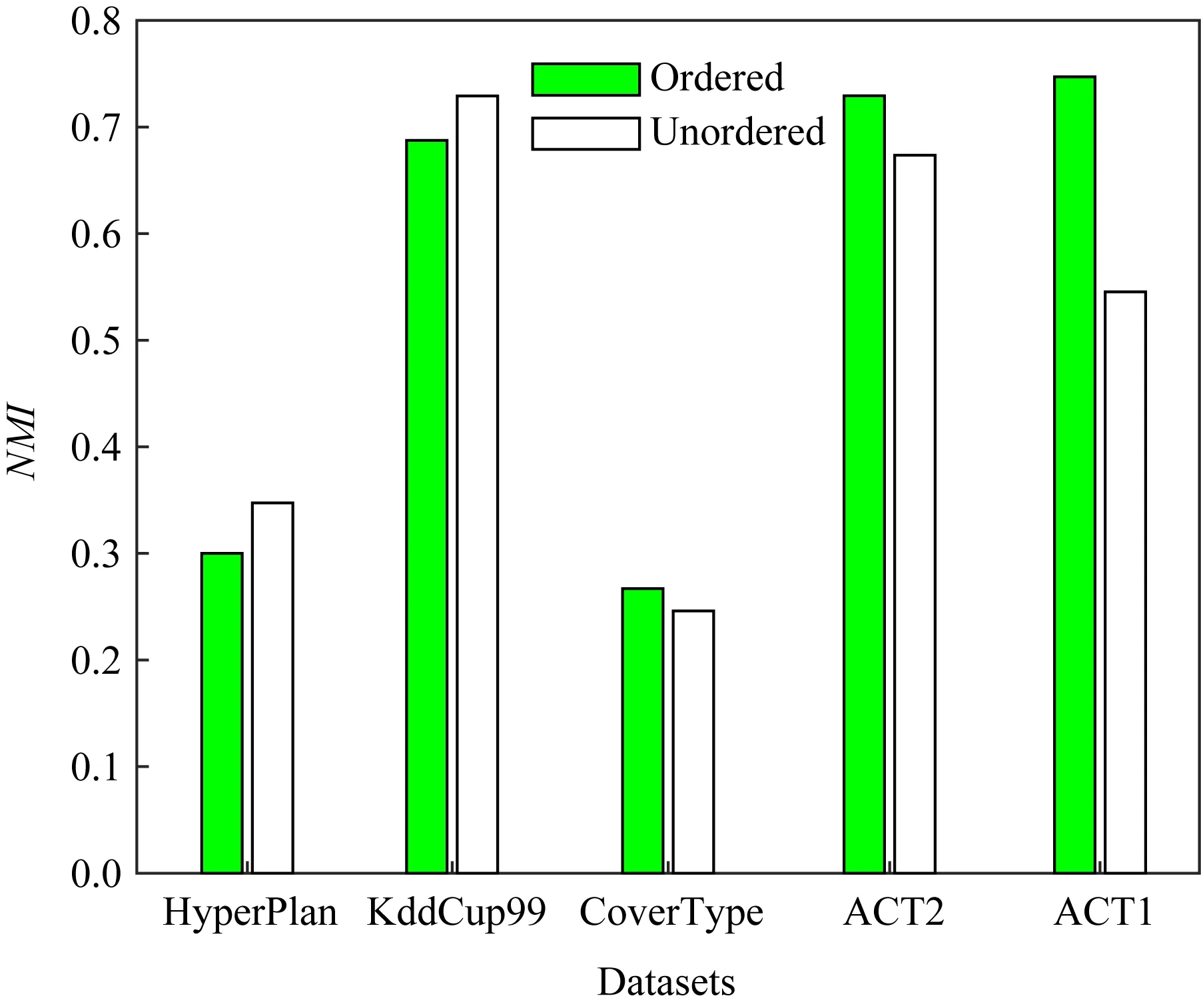
Fig. 4 NMI of RPFART with and without ordering of classes图4 RPFART在类排序与类未排序数据集上的NMI

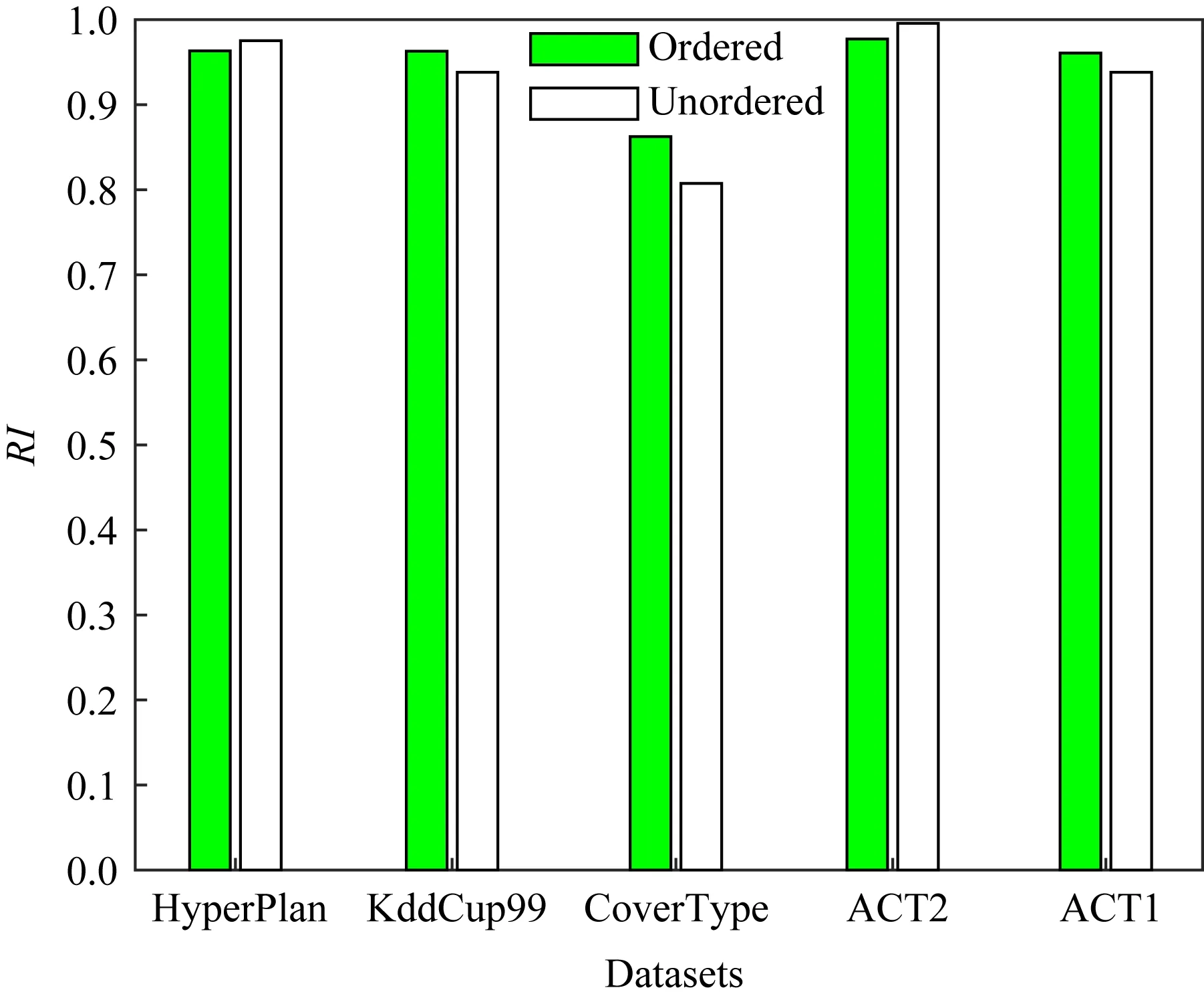
Fig. 5 Rand index of RPFART with and without ordering of classes图5 RPFART在类排序与类未排序数据集上的Rand指数

从图中可以看出：1)RPFART在类排序数据集上可以找到与类未排序数据集上相当的聚类纯度、NMI和Rand指数.特别是ACT2和ACT1数据集上甚至更优.2)仅KddCup99数据集上RPFART的聚类纯度值略有下降.基于以上结果，我们可以得出结论，不管数据是否按类标签排序到达，RPFART均可以有效地处理概念漂移问题.

3.7 警戒参数ρ的变化

图6显示了r=50%时RPFART在5个数据集上随警戒参数ρ的变化聚类性能的变化.

从图6可以看出：1)5个数据集上聚类纯度均随参数ρ的增大到达一定值后有所下降；2)在HyperPlan,CoverType,ACT2这3个数据集上NMI和Rand指数都随参数ρ的增大稳步增长，但KddCup99和ACT1数据集有下降趋势.

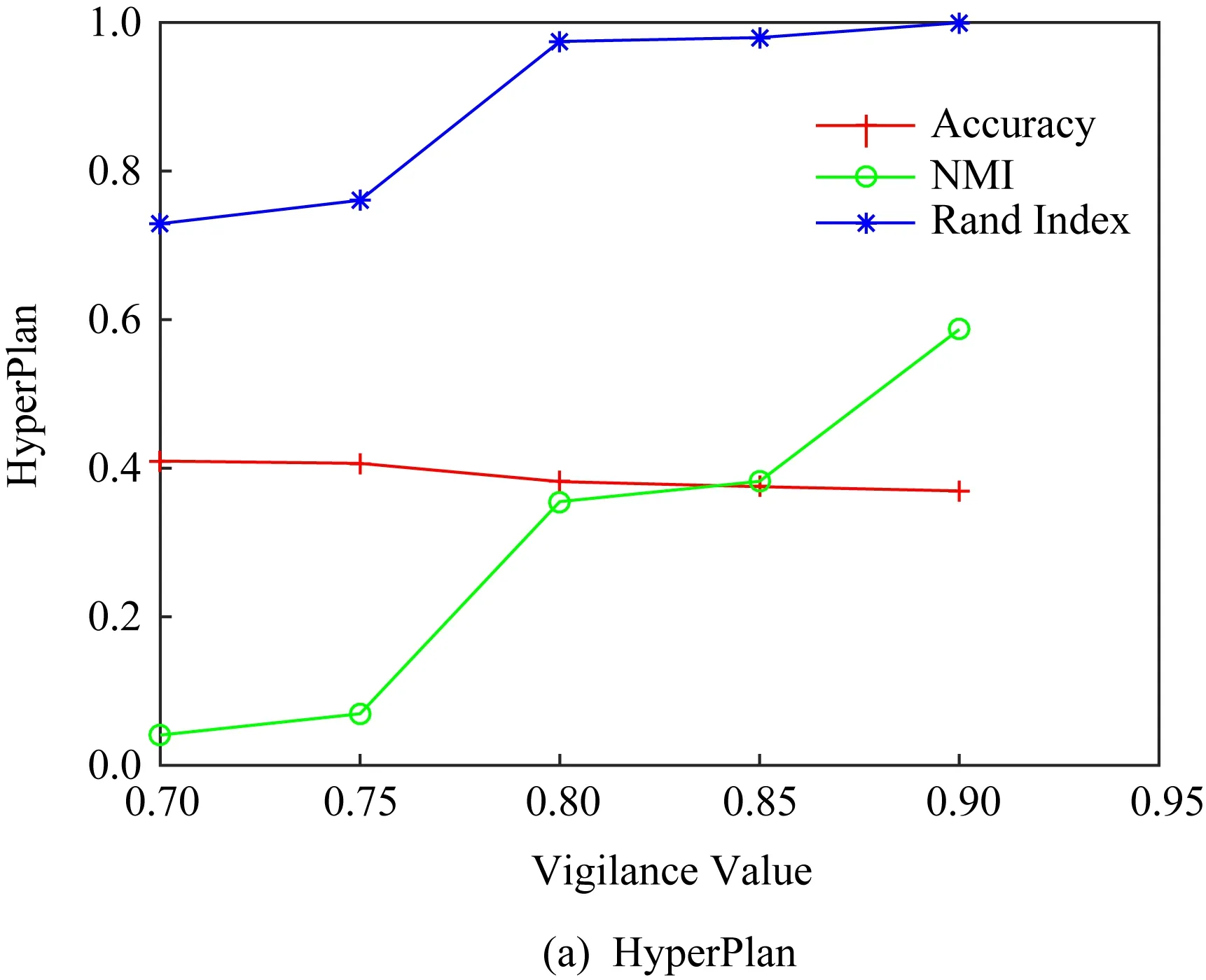
Fig. 6 Sensitivity of RPFART to vigilance value图6 警戒参数对RPFART算法影响

4 结 论

本文基于随机投影提出了高维数据流聚类算法RPFART.首先通过随机投影将原始高维数据映射到低维数据空间，再使用ART模型进行数据流聚类.ART具有线性计算复杂度，仅使用1个超参数，并对参数设置鲁棒.文中使用大量实验分析RPFART算法的聚类性能.多个数据集上的实验结果表明，即使原始尺寸压缩到10%，RPFART算法仍可以达到与RPGStream算法相当甚至更好的性能.对于ACT1数据集，其维数从67 500减少到6 750.