基于自适应邻域嵌入的无监督特征选择算法

刘艳芳 李文斌 高 阳

1(计算机软件新技术国家重点实验室(南京大学) 南京 210023)2(龙岩学院数学与信息工程学院 福建龙岩 364012)(liuyanfang003@163.com)

随着全球信息化的发展，许多应用领域得到的原始数据往往具有很高的特征维数.对高维数据的处理不仅增加了运算的时间复杂度和空间复杂度，也会导致学习模型的过拟合现象.而在高维数据中，只有部分特征是和学习任务相关的，同时，流形学习中验证高维空间的数据可以在低维空间表示[1]，因此，对这些高维数据进行降维是有必要的.

特征选择是一种重要的降维方法[2]，它一般是根据每个特征的重要性排序来选择特征子集，保留了原始特征的物理意义，为学习的模型提供了可解释性，这在许多研究领域是十分重要的.根据数据中是否有标签信息，特征选择分为监督特征选择[3-4]、半监督特征选择[5-6]和无监督特征选择[7-9].而在现实世界中存在大量的无标签高维数据，对这些数据进行标记是昂贵和耗时的，甚至是不可行的，比如医疗图像数据是需要非常专业的人士进行标注.因此，对无监督特征选择方法的研究是具有很大现实意义的.

近年来，国内外许多研究人员对无监督特征选择算法进行了大量的研究.在已有的无监督特征选择算法中，很多学者将k近邻法得到的样本相似矩阵嵌入到目标函数中，在高维无标记的数据集中得到了不错的结果.主要算法有：基于拉普拉斯打分的特征选择LS[10]根据同一类别数据较紧凑的特性，利用近邻得到数据的局部几何结构图，然后计算每个特征的得分选择特征；多类簇无监督特征选择MCFS[11]通过对拉普拉斯矩阵的谱分析获得特征之间的关系，然后利用1正则回归选择特征子集；无监督判别特征选择算法UDFS[12]基于样本可以由线性分类器分类的假设，采用k近邻挖掘的局部判别信息和2,1正则得到具有判别性的特征子集；基于非负谱分析的无监督特征选择算法NDFS[13]将k近邻得到数据的局部几何结构、谱聚类方法和正则结合起来，获得了更加精确的伪标签信息和判别性的特征子集；鲁棒的无监督特征选择算法RUFS[14]利用了鲁棒非负矩阵分解、局部学习、鲁棒特征学习，以及正则来处理标签和特征之间的关系，并删除冗余和噪声特征；自适应结构学习的无监督特征选择FSASL[15]为结构学习和特征选择提供了一个统一的框架，用特征选择的结果自适应更新结构信息，同时用更新后的结构去重新选择具有代表性的特征子集；冗余和噪声特征的存在导致原数据集得到的相似性矩阵不完全可信，因此，结构图优化的无监督特征选择算法SOGFS[16]融合了特征选择和局部结构学习，可以根据所选的特征子集自适应地更新相似性矩阵，并且通过约束相似性矩阵选择更有价值的特征；已有特征选择算法往往假设线性重构函数，而重构函数是依赖于数据本身的，而在高维情况下数据集往往是线性不可分的，因此，基于重构的无监督特征选择REFS[17]将重构函数的学习嵌入到特征选择过程中，同时，为保留原有特征结构，加入了拉普拉斯矩阵的正则项，进而选择具有判别性的特征子集；依赖指导的无监督特征选择算法DGUFS[18]给出了2种依赖关系：一种是原数据集和学习到的聚类标签集的依赖关系，另一种是所选择的特征子集和聚类标签的依赖关系，同时加入了2,0等式约束，进而获得具有代表性和判别性的特征子集；基于邻域保持学习的无监督特征选择[19]利用k邻域重构系数，引入中间矩阵构造低维空间，继而运用拉普拉斯乘子法优化目标函数，选择有效的特征子集；基于结构正则的自适应特征选择[20]首先用k邻域重构图，然后低秩约束重构图对应的拉普拉斯矩阵，并在优化过程学习重构图和所选特征矩阵，进而在过程中自适应局部结构；为了减少噪声数据对数据分布的影响，基于局部学习和组系数回归的无监督特征选择JLLGSR[21]首次结合基于局部学习的聚类和组稀疏正则项，并利用一个新的偏置项来提高模型的泛化性，进而选择相关的特征子集；基于广义不相关回归和自适应图的无监督特征选择URAFS[22]将通过最大熵得到的自适应图嵌入到流形学习中，并加入到广义不相关的回归模型中，通过闭式解得到不相关、无冗余的判别性特征子集；根据高维数据的稀疏性，文献[23]提出了鲁棒邻域嵌入的无监督特征选择RNE，通过k近邻构造系数矩阵，并加入1范数正则约束数据中的噪声和异常点，进而利用ADMM优化方法得到重要的特征子集；基于谱聚类的无监督特征选择FSSC[24]分别运用self-tuning[25]、样本标准差和距离矩阵[26]等3种自适应邻域方法对所有特征进行谱聚类，将相似性高的特征聚成一类，并通过特征的区分度与特征独立性之积度量特征重要性,从各特征簇选取代表性特征，构造特征子集.

已有的融合了流形学习、结构学习和谱聚类学习的无监督特征选择算法，大都采用k近邻得到局部相似矩阵或者相似图.然而，高维数据集大都不是均匀分布的，为每个样本选取相同而固定的近邻数是不能很好地适应每个样本的局部几何结构的.因此，本文提出了一种基于自适应邻域嵌入的无监督特征选择算法(adaptive neighborhood embedding based unsupervised feature selection, ANEFS).首先，根据数据集自身的稀疏稠密情况，为每个样本自适应地选择近邻数.其次，计算样本和其自适应邻域的权重系数，进而构造局部相似矩阵.然后，引入具有正交化的中间矩阵构建低维空间，并运用拉普拉斯乘子法选出有效的特征子集.最后，在公开的6个UCI数据集的实验结果表明，所提出的算法能够选出具有更高聚类精度和归一化互信息的特征子集.

1 自适应邻域

本节将介绍本文中使用的一些符号以及根据数据稀疏稠密情况构造自适应邻域.

1.1 符号说明

1.2 自适应邻域构造

通常运用k近邻法，采用欧氏距离，为每个样本找到k个近邻点.基于任何2个对象之间的欧氏距离不受分析中添加新样本的影响，同时，相较于其他度量方式，欧氏距离往往拥有较少的计算时间[27]，本文继续采用欧氏距离度量样本之间距离.然而，所有样本采用相同的近邻数，不能很好地适应每个样本的局部流形结构特征.文献[28]在样本固定、特征逐个到来的背景下根据数据自身的稀疏稠密情况自适应选择邻域，进而运用邻域粗糙集来选择特征.本文在文献[28]自适应邻域的基础上，明确使用的定义，并改进可接受的最大距离.首先，我们为数据集中的每个样本定义了一个有序序列.

list(xi)=(x(i,1),x(i,2),…,x(i,n-1)),

(1)

其中，Δ(xi,x(i,1))≤Δ(xi,x(i,2))≤…≤Δ(xi,x(i,n-1))，S={xi,x(i,1),x(i,2),…,x(i,n-1)}，Δ(xi,xj)是样本xi和样本xj之间的欧氏距离.

如果数据集X服从均匀分布，将Δ(xi,x(i,n-1))分成n-1段，那么每一段中应包含一个样本.在实际应用中，数据集往往不是均匀分布的.为了根据数据集实际分布寻找邻域，我们在有序序列的基础上，根据每个样本和其他样本之间的最大距离和最小距离，即样本自身的稀疏稠密情况来定义样本的自适应邻域.简单起见，我们将Δ(xi,x(i,j))记为Δi(x(i,j)).

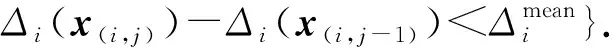
(2)

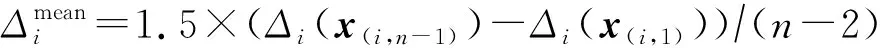
1.3 人造数据集的自适应邻域分析

Fig. 1 Neighbors based on kNN and the adaptive neighborhood图1 基于k近邻和自适应邻域构造法的近邻点分布

由图1(a)可知，原始50个样本点是非均匀分布的，其中样本a处数据样本分布稀疏，样本b相对于样本a处数据样本分布更为稀疏，而样本c处数据样本分布较为稠密.图1(b)为k=5时k近邻法得到的近邻分布结果，样本a，b和c的近邻数均相等，无法反映数据分布的稠密稀疏情况.图1(c)是根据式(2)得到的自适应邻域分布结果，从图中可以看到，样本，和的近邻样本数分别为4，1和18.因此，可以说明，自适应邻域构造方法得到的邻域个数已经考虑到数据分布的稀疏稠密程度.

2 自适应邻域嵌入的特征选择算法

运用k近邻法得到的样本相似矩阵可以捕获到比全局结构更加关键的局部几何数据结构[29].在无监督特征选择中，很多学者将k近邻法得到的样本相似矩阵嵌入到目标函数中，在高维无标记的数据集中得到了不错的结果.然而，k近邻法得到的局部几何结构不能反映数据分布的稠密稀疏情况.因此，本文将反映数据分布情况的自适应邻域引入到无监督特征选择算法中，提出了基于自适应邻域嵌入的无监督特征选择算法(adaptive neighborhood embedding based unsupervised feature selection, ANEFS).

自适应邻域嵌入的无监督特征选择算法分为4部分：1)利用式(2)中的自适应邻域构造方法得到数据样本的近邻点；2)求解每个样本的权重系数向量；3)引入中间矩阵构建低维空间；4)运用拉普拉斯乘子法选出有效的特征子集.

2.1 构造自适应邻域集

不同于k近邻法，定义2中数据集中每个样本点获得的自适应邻域个数是不同的，能够反映出数据集的样本稀疏稠密情况.

算法1.自适应邻域集.

输出：自适应邻域集AN(xi).

① 运用欧氏距离，分别计算样本xi与样本x1,…,xi-1,xi+1,…,xn的距离，得到距离向量disi；

② 升序排列更新disi，并得到xi的有序序列list(xi)；

④ 根据list(xi)，采用式(2)计算xi的自适应邻域集AN(xi)；

根据上述的算法1的步骤，每步的时间复杂度分别为：步骤①中计算一个样本与其他样本间的距离需要O(nd)；步骤②对距离进行排序需要O(nlogn)；步骤③和④计算最大可接受均值，并寻找一个样本的自适应邻域需要O(1+n).因此，算法1的整体时间复杂度为O(nd+nlogn+1+n).在高维数据下，特征维数d大于样本数n，则算法1的时间复杂度是O(nd).

2.2 求解自适应邻域权重系数

求解每个数据样本与其自适应近邻点之间线性关系的权重系数，可以形式化为一个回归问题.采用均方差作为目标函数，即:

(3)

其中，wi=(wi1,wi2,…,wi|AN(xi)|)T是|AN(xi)|维的列向量，|AN(xi)|是xi自适应邻域的个数.为了方便求解，我们将式(3)转换为形式:

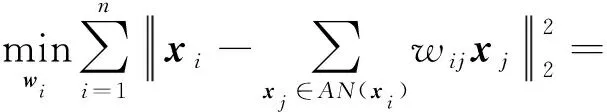
(4)

(5)

其中，zi=(xi-xj)(xi-xj)T，xj∈AN(xi)，λ≥0是一个常数.式(5)对wi(i=1,2,…,n)进行求导:

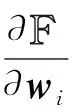
(6)

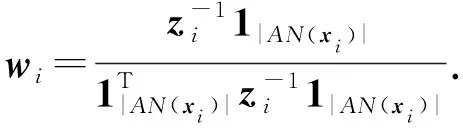
2.3 基于自适应邻域嵌入的低维空间

其中，x(i,k)是定义1中样本xi的有序序列list(xi)中的第k个样本.式(8)中是数据集在原有高维空间根据自适应邻域构造方法得到的样本相似权重系数.根据式(8)，可以将式(3)等价形式化为

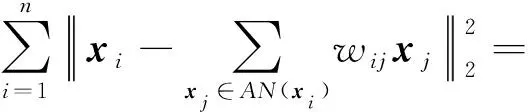
(9)

为了保持原始样本集的局部几何结构，即相似矩阵S在低维空间中保持不变，通过选出有效的特征子集I⊆F，构造低维空间的最小误差可表示为

根据式(11)可知，中间矩阵H的每一行的元素中有且只有一个元素为1，其他全部为0，因此，中间矩阵H是正交矩阵，即HHT=Im.则式(10)可以转换为

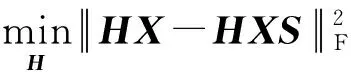
(12)

2.4 优化目标函数

(13)

其中，M=X(In-S)(In-S)TXT.式(13)对H进行求导并令其等于0，同时，根据约束条件HHT=Im，则有：

(14)

即：

MHT=μHT.

(15)

从式(15)中可知，HT和μ是由矩阵M的特征向量和特征值构成的.为了从数据中选择有效的特征子集，只需取M中最小的m个特征值对应的特征向量.

算法2.自适应邻域嵌入的无监督特征选择算法.

输出：特征子集I.

① fori=1:n

② 调用算法1，寻找样本xi的自适应邻域集AN(xi)；

③ 根据式(7)，计算样本xi与AN(xi)中样本的相似权重系数wi；

④ end if

⑤ 根据式(8)，构造数据集中样本相似矩阵S；

⑥ 计算矩阵M=X(In-S)(In-S)TXT的特征向量矩阵V和特征值矩阵μ；

⑦ 根据μ的升序更新V，令更新后的V=(v1,v2,…,vd)，其中vi是d维度列向量，则HT=(v1,v2,…,vm)T；

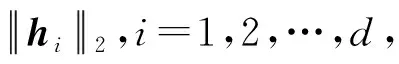
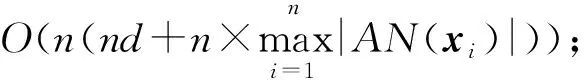
3 实验与结果分析

实验选用了6个公开数据集对算法进行测试研究，实验数据集可从FEATURE SELECTION DATASETS(1)http://featureselection.asu.edu/datasets.php中获取.数据集详细信息如表1所示，其中，Yale，warpAR10P和orlraws10P是人脸数据集，GLIOMA和ALLAML属于基因表达数据集，madelon属于人工数据集.

3.1 实验参数设计

为了验证提出的自适应邻域嵌入的无监督特征选择算法ANEFS的性能，实验比较了ANEFS与基于拉普拉斯打分的特征选择LS[10]、多类簇无监督特征选择MCFS[11]、自适应结构学习的无监督特征选择FSASL[15]、基于重构的无监督特征选择REFS[17]、依赖指导的无监督特征选择DGUFS[18]、基于广义不相关回归和自适应图的无监督特征选择URAFS[22]以及选择所有特征(Baseline)在表1数据集的实验结果.对比算法LS和MCFS采用热核相似性度量特征相似性，带宽参数t=1.根据相关参考文献中的参数敏感分析，选用文献中运行结果较好的参数设置，其中，对比算法FSASL中控制全局结构的参数α=0.01，控制局部结构的参数β=0.1，控制特征选择的稀疏性参数γ=0.1；对比算法REFS中惩罚没有被选择的特征重构错误的参数α=0.1，控制重构后保持原有特征结构的参数β=0.1；对比算法DGUFS中控制学习得到的聚类标签相关矩阵的低秩参数α=100，控制原数据集、学习得到的聚类标签和所选特征子集之间内部依赖关系的参数β=0.5；对比算法URAFS中控制图正则项的参数α和最大熵得到的相似矩阵的参数β均设置为1，控制特征选择的行稀疏性参数λ=100.同时，除了本文提出算法ANEFS的近邻数是根据数据集本身的分布自适应得到以及URAFS中是优化自适应的，其他对比算法LS,MCFS,FSASL,REFS,DGUFS的近邻数k均设置为5.对所有的数据集，特征选择的个数设置为{20,30,…,100}.实验选用K-means算法进行聚类，而K-Means算法对初始选取的聚类中心点是敏感的，因此，K-means算法对选取的特征子集运行30次实验记录平均值.

3.2 度量标准

为了验证算法的有效性，文中采用2种判断标准：聚类精度(clustering accuracy,ACC)和归一化互信息(normalized mutual information,NMI)，来衡量不同算法选择不同特征子集时的效果，其中，ACC和NMI的值越大表示算法效果越好.

1) 聚类精度(ACC)：

其中，n为样本数，l(xi)和l′(xi)分别为样本xi自带的类别标签和聚类算法得到的类别标签，δ(x,y)是指示函数，当x=y时，值为1，否则为0.

2) 归一化互信息(NMI)：

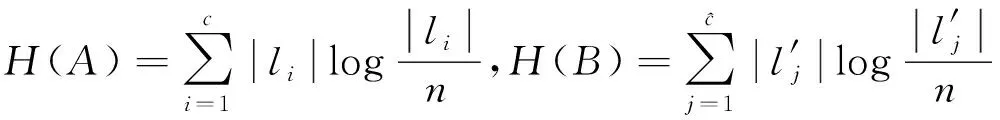
3.3 实验结果分析

本节比较了所提的ANEFS算法与6种无监督特征选择算法LS,MCFS,FSASL,REFS,DGUFS和URAFS在表1数据集上的性能，并对性能指标值进行了分析.

3.3.1 示例分析

本节展示了所提算法ANEFS的效果示例图.首先，随机地从Yale数据集中选择2个样本作为示例.然后，在这2个样本上执行ANEFS算法，并分别选择出20,40,60,80,100个特征.为了便于说明，所选择的特征用白色“方框”表示，未被选择的特征保留原有的值，如表2所示.从表2可以看出，所提出的ANEFS算法所选择的特征是相对集中的，并且倾向于选择有辨别性的部分，如眼、唇和脸颊，可以描述一个人脸的特性.这也意味着所提算法在一定程度上可以得到最优的特征子集.

Tabel 2 Toy Examples of ANEFS on Yale Dataset表2 ANEFS算法作用在Yale数据集上的示例图

3.3.2 实验结果分析

由于所选最优特征数目是未知的，为了更好地评估无监督特征选择算法的性能，我们记录了在不同特征子集上最好的结果.表3和表4分别记录了不同算法在表1的6个数据集上最高的聚类精度和归一化互信息结果，其中最好的结果用粗体表示，次优用下划线标注，最后一行是各个算法在6个数据集上的平均结果.与保留全部特征(Baseline)的聚类性能相比，这些无监督特征选择算法不仅大幅度的降低了特征维数，而且提高了聚类效果.尤其是所提算法ANEFS选择了15%以内的特征数在聚类精度和归一化互信息上分别提高了7.84%和10.8%，这表明ANEFS选择的特征子集相对具有代表性和判别性.同时，ANEFS在平均聚类效果上优于其他6种无监督特征选择算法，其中，聚类精度上提高了4.29%～9.68%，归一化互信息上提高了7.88%～11.75%.

Table 3 Maximum Clustering Accuracy (%) of the Compared Algorithms表3 无监督特征选择对比算法的最大聚类精度

Table 4 Maximum Normalized Mutual Information (%) of the Compared Algorithms表4 无监督特征选择对比算法的最大归一化互信息

图2和图3分别所提ANEFS算法、对比算法LS,MCFS,FSASL,REFS,DGUFS,URAFS以及全部特征Baseline在表1的6个数据集上对应不同特征数目的实验结果.从图2和图3的实验结果中，我们可知在人脸数据集Yale,warpAR10P,orlraws10P和基因数据集ALLAML上，所提算法ANEFS的聚类精度和归一化互信息绝对的优于其他6种对比算法，较大的提高了聚类效果.在基因数据集GLIOMA上，除了对比算法DGUFS，所提算法ANEFS的聚类效果优于其他对比算法.在人工数据集madelon上，ANEFS选择特征数目为70或者80时聚类性能优于其他对比算法.

Fig. 2 Relationships between clustering accuracy of compared algorithms and the number of selected features图2 对比算法的聚类精度与特征选择数目的关系

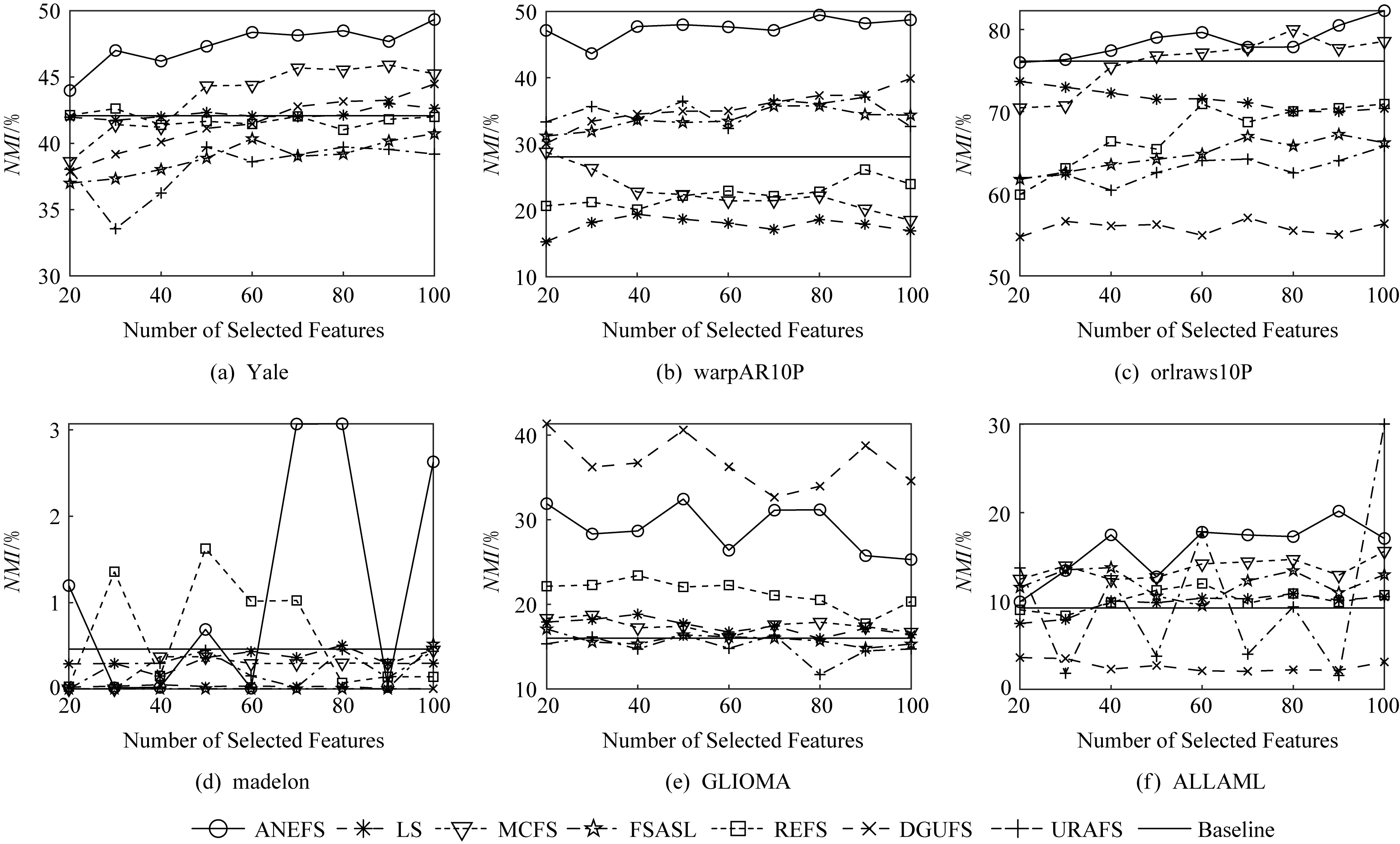
Fig. 3 Relationships between normalized mutual information of compared algorithms and thenumber of selected features图3 对比算法的归一化互信息与特征选择数目的关系

综合表3,4和图2,3的对比信息可知，所提算法ANEFS在数据集上只需选择较少的特征数量就能达到不错的效果.从总体性能上，对比LS,MCFS,FSASL,REFS,DGUFS和URAFS等6种无监督特征选择算法和保留全部特征(Baseline)，本文所提ANEFS的聚类效果更好.这可能的原因可以归结为2点：1)降维后的数据集保持了原有数据集的局部几何结构；2)ANEFS采用的是能捕捉原数据集稀疏稠密的局部几何结构，而LS，MCFS，REFS，DGUFS这4种对比算法都采用了忽略数据集分布结构的固定邻域数目，FSASL和URAFS算法在优化过程中自适应学习局部结构，但FSASL依旧固定了邻域数目，URAFS是通过最大熵得到相似矩阵，均不能很好地捕捉数据本身的局部结构.

4 总 结

本文提出了一种基于自适应邻域嵌入的无监督特征选择算法，根据数据样本自身的稀疏稠密情况来确定去其近邻数，进而构造样本相似矩阵，同时，通过引用具有正交性质的中间矩阵，从原始空间直接选取特征子空间得到低维空间，从而实现在低维空间进行高维数据的聚类分析.实验表明：本文提出的算法可以取得更好的聚类效果.本文将能接受的自适应邻域距离由样本与其他样本的最大、最小距离来确定，接下来需要进一步探索更好的自适应邻域选取方法，同时，重构系数矩阵在学习过程中是保持不变的，会进一步探索在优化过程中采用自适应邻域的结果.