基于邻域多核学习的后融合多视图聚类算法

夏冬雪 杨 燕 王 浩 阳树洪

1(西南交通大学信息科学与技术学院 成都 611756)2(广西科技大学计算机科学与通信工程学院 广西柳州 545006)(vdx_swjtu@126.com)

机器学习的许多实际问题中，研究对象常由不同来源的数据或不同特征进行刻画.例如不同机构对同一新闻事件的各自报道，同一图像的不同特征表示，同一故事的视频或文字描述.类似场景中，从不同视角对同一对象集合进行描述的数据，称之为多视图数据[1].多视图学习利用多视图数据来获得对象的全面理解，可以克服单视图数据可能导致的偏差或不足，因而成为近年的研究热点[2].同时，在当前大数据时代，数据产生和收集的速度迅猛增长，人工标注变得非常昂贵和不切实际，聚类分析作为一种重要的无监督学习形式，日益受到研究者的广泛关注.本文主要关注多视图聚类.已有研究表明:多视图聚类能够充分利用视图之间的互补性和一致性，从而产生比单视图聚类更为精确和健壮的数据划分[3-4].

现有的多视图聚类算法大致包括典型相关分析、多视图矩阵分解、图谱聚类等类别[1].近年来，许多基于图谱理论的算法被陆续提出并取得良好效果[3,5-7].这些方法通常以分步进行的方式完成多视图聚类，即首先构造每个视图的相似图S(similarity graph)，然后学习所有视图的公共相似图，最后对得到的公共相似图进行聚类分析[3,6].

上述基于图谱理论的多视图聚类算法在许多场景中被证明是有效的，但仍存在3个缺陷.1)信息融合可在原始数据级、特征级和决策级进行，构建公共相似图的算法本质上是特征级的信息融合[3,7].然而，从相似图的性质来看，一者不同视图描述对象的视角、聚类能力存在较大差异[8]；二来由于实际应用中广泛存在的信息缺失、噪声等因素容易造成某个视图的相似图失真，强制所有视图共享一个公共相似图可能导致最终聚类结果不理想[6].2)目前基于图谱理论的多视图聚类多以分步形式完成：即先构造公共相似图，然后据此进行聚类.而不是在一个统一的过程中优化这2个任务，从而可能导致额外的PAC(probably approximately correct)边界[3,9].3)对于数据中广泛存在的非线性关系，尽管已有若干工作采用核方法进行有效处理，但大多基于全局自表达学习的框架进行核变换[10]，基于局部结构进行多核学习的方法仍鲜见报导.然而，局部结构对于聚类分析和非线性关系建模有重要意义[11-12].具体表现包括：在足够小的邻域范围内，样本间非线性关系通常能用局部线性嵌入一阶逼近，样本的聚类标签可用近邻回归进行预测[12-13]；在稍大的局部范围内，虽然低维输入空间中数据样本分布呈现出非线性流形关系，但若将其嵌入到高维特征空间中，则数据样本在高维空间中的分布仍与欧氏空间局部同胚，从而在局部范围内仍可借鉴欧氏空间的相关理论方法进行建模与分析[13].

因此，本文提出一种基于邻域多核学习的后融合多视图聚类算法(local multi-kernel learning based late fusion multi-view clustering, LMLFMC).其主要贡献包括3个方面：

1) 与基于全局自表达的核方法不同，本文仅考虑近邻数据，无需学习整个数据集的自表达关系，从而在保持局部非线性结构的同时减轻计算负荷.

2) 尽管各视图的相似图可能存在差异，但不同视图的数据是从不同角度描述同一个样本集合，其簇类划分结构是跨越不同视图的全局结构，本文模型将信息融合推迟到数据划分空间进行，因而比基于相似图融合的多视图聚类模型更加鲁棒.

3) 本文模型在一个统一的框架下，对多核组合方式、各个视图的相似图构造及最终的簇类结构划分进行协同优化，从而使得上述子任务能以相互促进的方式迭代提升模型整体性能.

1 相关工作

由于多视图数据的广泛应用，近年来，许多将基于图谱理论的聚类模型扩展到多视图的算法被不断提出[7,14-17].Saha等人[14]首先构造视图的子空间表示，然后在公共子空间实现多视图聚类，但没有考虑不同视图的权重.针对此问题，Nie等人[7]首先生成每个视图的相似图，然后以不同权重将其整合得到一个公共相似图，再在公共相似图上进行聚类分析.后续若干算法对此进行持续研究，提出一系列更为有效的方法[15-16].这些方法并不需要附加的K-means步骤，但仍以分步进行的方式完成信息融合：即首先生成各视图的相似图，保持不变，然后再进行信息融合.此外，上述基于图谱理论的多视图聚类方法强制所有视图统一到一个公共相似图，而该公共相似图并没有以最终的簇类划分为目标进行优化，从而导致对后者而言，该公共相似图并非最优.为了减轻相似度矩阵的计算负担，Wang等人[17]采用数据簇相似度矩阵计算数据点和簇中心之间、而不是对数据点之间的相似度，尽管该方法可以提高计算效率，但仍需一个附加的聚类步骤来获得最终的簇类划分.

本文模型采用谱旋转实现多视图信息的后融合.Yu等人[18]首次采用谱旋转实现多类别划分.Zelnikmanor等人[19]在此基础上提出自适应谱聚类.Huang等人[20]综合比较了谱聚类框架下的谱旋转和K-means算法，提出了一种基于谱旋转的谱聚类算法.Nie等人[6]用谱旋转代替K-means聚类步骤，将文献[20]中的算法推广到多视图聚类，但仍以分步方式完成多视图聚类，即先构造各视图的相似图，在后续的聚类过程中这些相似图保持固定，这可能导致所构造的相似图对于后续的聚类任务并非最优.

核方法由于能有效建模数据点之间的非线性关系而被广泛应用到聚类分析中.Scholkopf等人[21]提出了核K-means聚类算法，Zhang等人[22]将其扩展为基于核PCA的通用核学习框架.Langone等人[23]将核方法引入到谱聚类.上述基于单个核函数的模型的性能严重依赖于核函数的选择.然而，从预定义的函数库中选择最佳核函数非常耗时甚至不切实际.为解决这一问题，Kang等人[24]采用多核学习对多个核函数进行优化加权，从而无需预先选择最佳核函数.此后，Huang等人[10]提出一种基于多核学习的多视图聚类算法.已有研究表明：局部结构对于聚类分析和非线性关系学习有重要意义[11-13].但上述基于核方法的聚类模型，均基于全局自表达学习方案，即在核空间中学习所有样本对于特定样本的全局线性表达，该方法不利于充分挖掘数据间的局部结构，且对于在高维空间进行表达学习的核方法而言，由于需要计算所有数据点的表达系数，从而带来巨大的计算负荷.

2 本文模型

2.1 核空间中的邻接矩阵构造

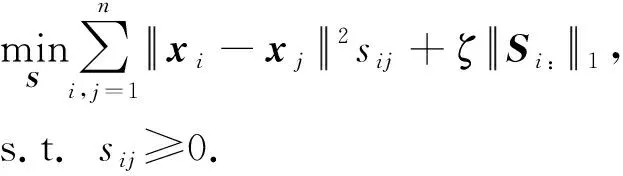
对邻接矩阵S进行归一化，使得ST1=1，则式(1)的第2项成为常数项，即此处的归一化操作等价于对S进行稀疏化约束.故问题式(1)可改写为

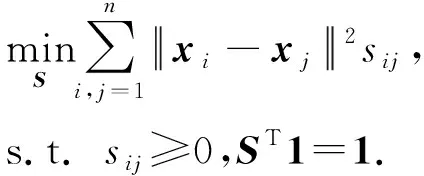
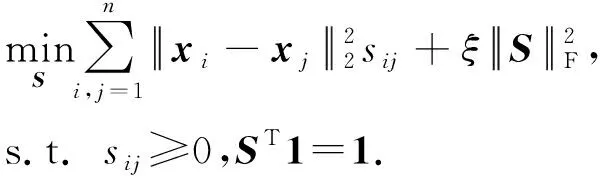
上述邻接矩阵S的构建基于原始输入空间的欧氏距离.采用该距离测度进行聚类，通常要求数据集本身线性可分[26]，而该条件在真实数据上往往难以满足.为克服该局限性，本文用核技巧将输入空间的数据映射到高维特征空间，以提高数据的可分离性.

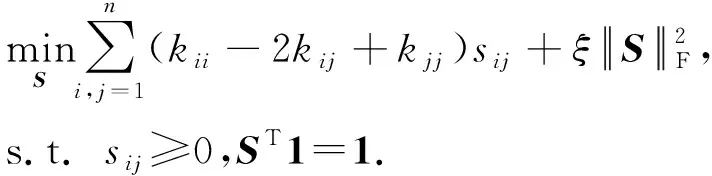
可验证，式(3)是式(4)采用线性核时的一个特例.

2.2 低秩约束的单视图聚类

通过求解问题式(4)，可得到每个视图的相似图Sv，继而通过谱聚类进行聚类分析.然而，传统的谱聚类需要一个附加的K-means步骤来获得最终的聚类结果，而这个附加的聚类步骤可能会带来额外的PAC边界[9].故此，本文提出一种在统一框架下对相似图构造和聚类分析进行协同求解的方法，使得所构造的相似图的连通分量数目正好等于聚类数目，从而省除附加的K-means步骤.

定理1.拉普拉斯矩阵LS的特征值0的重数c等于S所对应的图中连通分量的个数.

定理1在聚类分析中的意义在于，如果拉普拉斯矩阵的秩rank(LS)=n-c，则对应的图正好包含c个全连通分量，因此不需要附加的K-means步骤就可以得到最终的聚类结果.

受定理1的启发，本文对问题式(4)添加一个低秩约束，使得所构造的相似图的连通分量数目正好等于聚类数目，即：

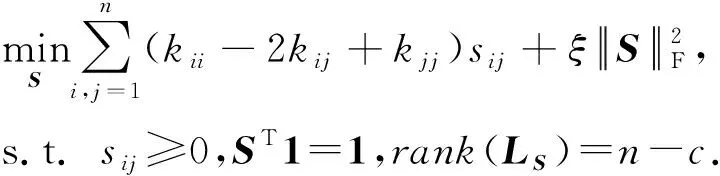
由于低秩约束不易处理，且LS依赖于优化变量S，直接求解问题式(5)非常困难.然而，由于LS是半正定矩阵[27]，问题式(5)可转化为易于求解的等价形式.

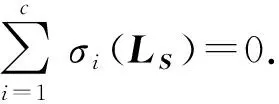
(6)

将式(5)中的约束rank(LS)=n-c用式(6)进行替换，问题式(5)转换为

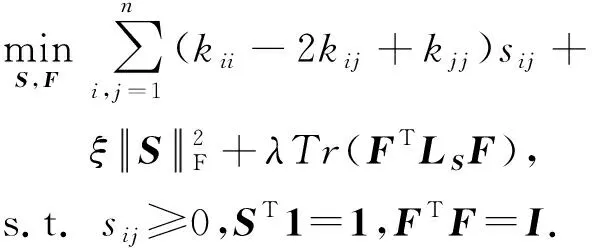
当问题式(7)中的参数λ设置为一个足够大的值时，其解F*可使问题式(5)中约束rank(LS)=n-c得到满足.

2.3 基于谱旋转的后融合多视图聚类

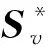
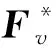
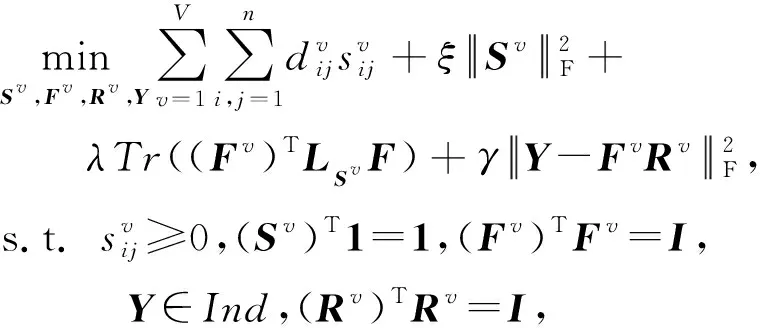
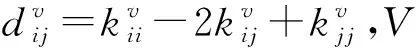
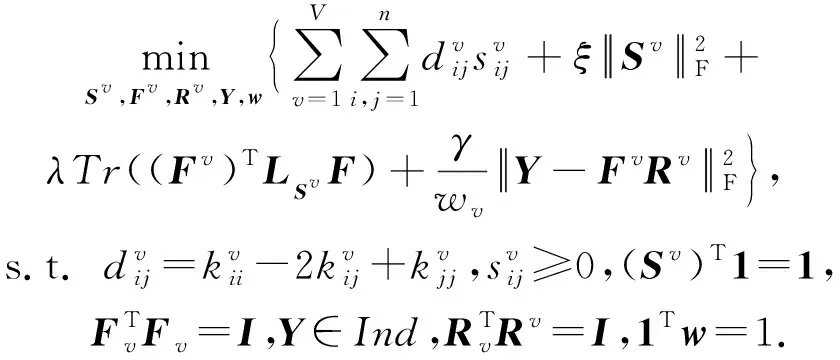
从上述分析可知，本文模型是对谱嵌入矩阵而不是样本邻接矩阵进行信息融合.

2.4 基于多核学习的后融合多视图聚类

虽然式(9)描述的模型可在核空间中以统一框架学习邻接矩阵和聚类指示矩阵，但仍面临核函数的选择问题：核方法的性能与核函数的选择高度相关.但针对特定问题预先选择一个最佳核函数非常困难.在多视图学习中，此问题更加棘手，因为各视图的数据之间的非线性关系可能互不相同，对于某个视图而言最佳的核函数却不一定适用于另一个视图.为了克服单个核函数的局限性，本节将式(9)描述的单核模型扩展到多核，用多个预先定义的核函数自动学习最佳核函数组合，从而避免核函数选择的问题.

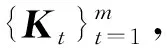
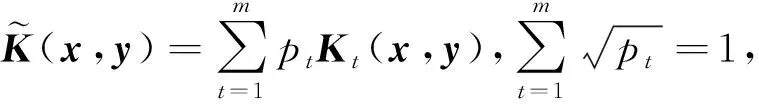
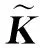
将式(10)代入式(9)，并调整参数位置，最终得到本文基于多核学习的后融合多视图聚类模型：

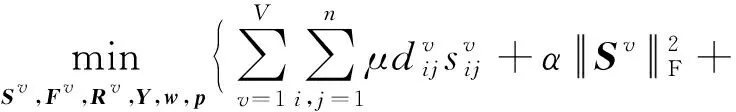
(11)

3 模型求解

因目标函数式(11)中的优化变量相互耦合、包含离散变量Y，且约束亦不平滑，故求解式(11)并不容易.本文提出一个交替迭代的优化方案求解式(11).下文按优化变量具体介绍其各自更新规则.

3.1 固定其他变量，对每个视图更新Sv

当其他与Sv无关的变量保持不变时，问题式(11)的目标函数关于Sv可加，且关于Sv的约束也可按视图分离.因此，可独立对每个视图依次更新Sv.省略视图上下标，则式(11)可改写为

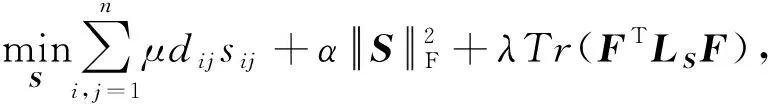
(12)

通常仅保留数据点xi与其最近邻的若干个数据点之间的边，是以在保持邻接矩阵S的稀疏性的同时降低计算复杂度[3,30].若为数据相似图中的每个节点保留k个邻居，即邻接矩阵S每行仅保留k个非零元素，则S的更新方案为

(13)

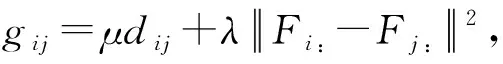
3.2 固定其他变量，对每个视图更新Fv

与Sv类似，当其他变量保持不变时，Fv亦可依视图进行独立更新，则式(11)可改写为

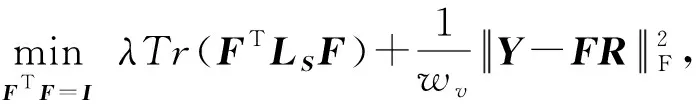
因为此处LS，Y，R皆为常量，式(14)可变换为

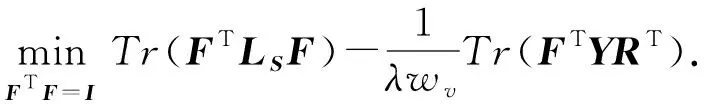
问题式(15)是一个典型的Stiefel流形上的二次优化问题(quadratic problem on the Stiefel manifold, QPSM)[31].由于式(15)的目标函数的Hessian矩阵LS为半正定矩阵，所以式(15)是一个凸问题，其全局最优解F*必然存在.若干学者对QPSM进行了深入研究，提出了若干高效稳定的迭代算法，可用于求解式(15)[31-32].

3.3 固定其他变量，对每个视图更新Rv

类似地，Rv亦可依视图独立更新.当其他变量保持不变时，式(11)可变换为

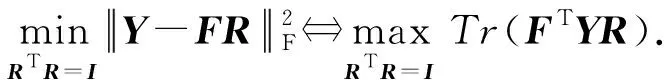
该问题的解析解为[31]

R+=UVT,

(17)

其中，U和V分别为FTY的SVD分解的左右奇异向量.

3.4 固定其他变量更新核函数权重向量pv

类似地，核函数权重向量pv也可依视图独立更新，此时式(11)等价于：

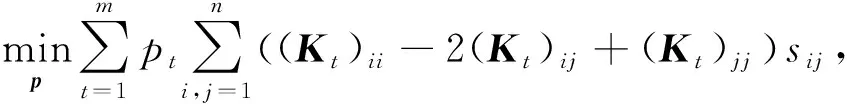
(18)

定义向量z,其第t个分量为

则式(18)可等价变换为

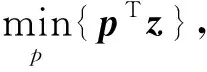
(19)

问题式(19)的拉格朗日函数为

(20)

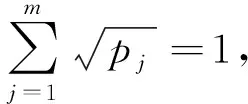
(21)

3.5 固定其他变量更新聚类指示矩阵Y

固定其他所有变量，对式(11)求解Y等价于：

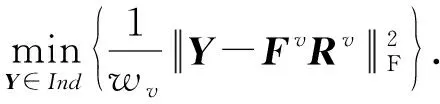
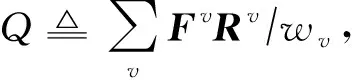
(23)

因Y为类别指示矩阵，显然式(23)有解析解为

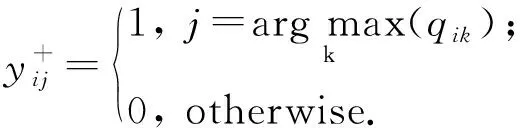
3.6 固定其他变量更新视图权重向量w

固定其他所有变量，对式(11)求解w等价于：

(25)

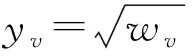
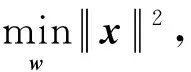
(26)

问题式(26)可求解如下.据Cauchy-Schwarz不等式有：

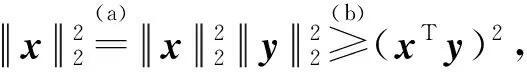
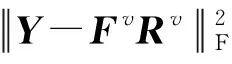
(28)

将式(28)的结论回代到问题式(25)，简单计算可得：

(29)

总结本文模型(LMLFMC)的求解算法.

算法1.LMLFMC.

输入：多视图数据Xv、邻居个数k、类别数c、参数μ和λ、最大迭代次数tmax;

输出：类别指示矩阵Y.

① 初始化：t=0，生成核矩阵，初始化w,p.

② 对每个视图Xv：

按式(13)更新Sv;

求解子问题式(15)更新Fv；

按式(17)更新Rv；

按式(21)更新核矩阵权重向量pv.

③ 按式(24)更新Y；

④ 按式(29)更新视图权重向量w；

⑤ 重复②～④直到最大迭代次数.

4 实验与结果分析

4.1 实验方案

实验环境为Intel Xeon Gold 6254@3.10 GHz(X2)CPU,768 GB RAM,2×Tesla V100 GPU.操作系统为Windows Server 2019,编程语言为Matlab.

本文选取6个多视图聚类中广泛采用的公开数据集进行实验：文本数据集3source和BBC,图像数据集Caltech101_7,100leaves和ALOI,以及网络文本数据集WebKB.详情如表1所示：

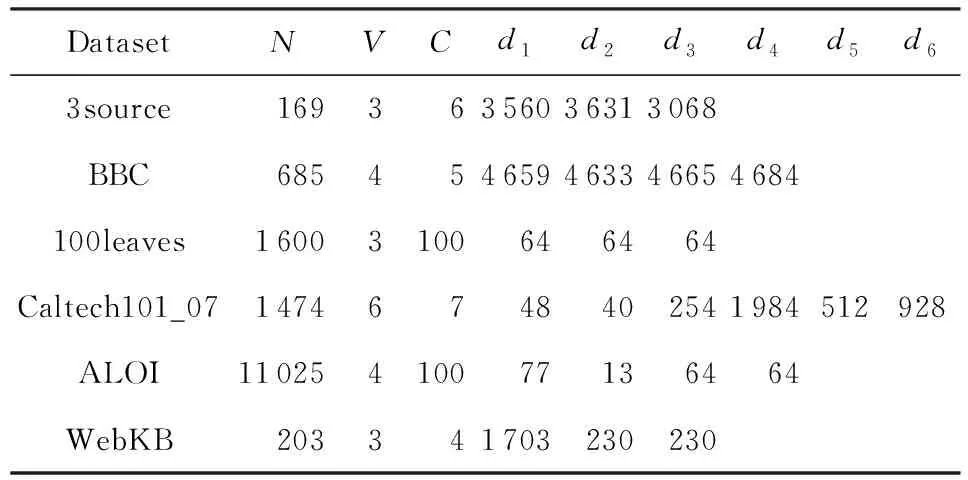
Table 1 Detailed Information of Benchmark Datasets表1 基准数据集详细信息

表1中N、V、C分别代表数据集的样本个数，视图个数和类别数.di代表第i个视图的特征维数.

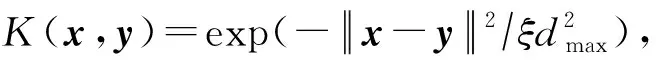
本文选取了多个代表性多视图聚类算法进行对比分析.包括：MKC(multi-viewK-means clustering)[33]，MVCNMF(multi-view clustering via non-negative matrix factorization)[34],CRSC(co-regularized spectral clustering)[35]，RMSC(robust multi-view spectral clustering)[36]，ASMV(adaptive structure-based multi-view clustering)[16]，AMG(auto-weighted multiple graph-learning)[7]，MKMVC(multi-kernel multi-view clustering)[10]，MGFSC(multi-graph fusion spectral clustering)[8].同时，也将标准谱聚类SC(spectral clustering)[37]应用到每一个视图，并给出SC在各单视图的最佳和最差结果.所有算法运行10次，给出结果的均值和方差.

4.2 实验结果分析

本文采用ACC,MNI,F-measure和ARI这4个指标进行聚类效果评价.实验结果如表2～7所示.其中SC_w(Vi)和SC_b(Vj)分别表示将SC应用到相应数据集的各个单视图，分别在第i个和第j个视图上得到的最差(worst)和最佳结果(best).最好的2个结果用黑体显示.

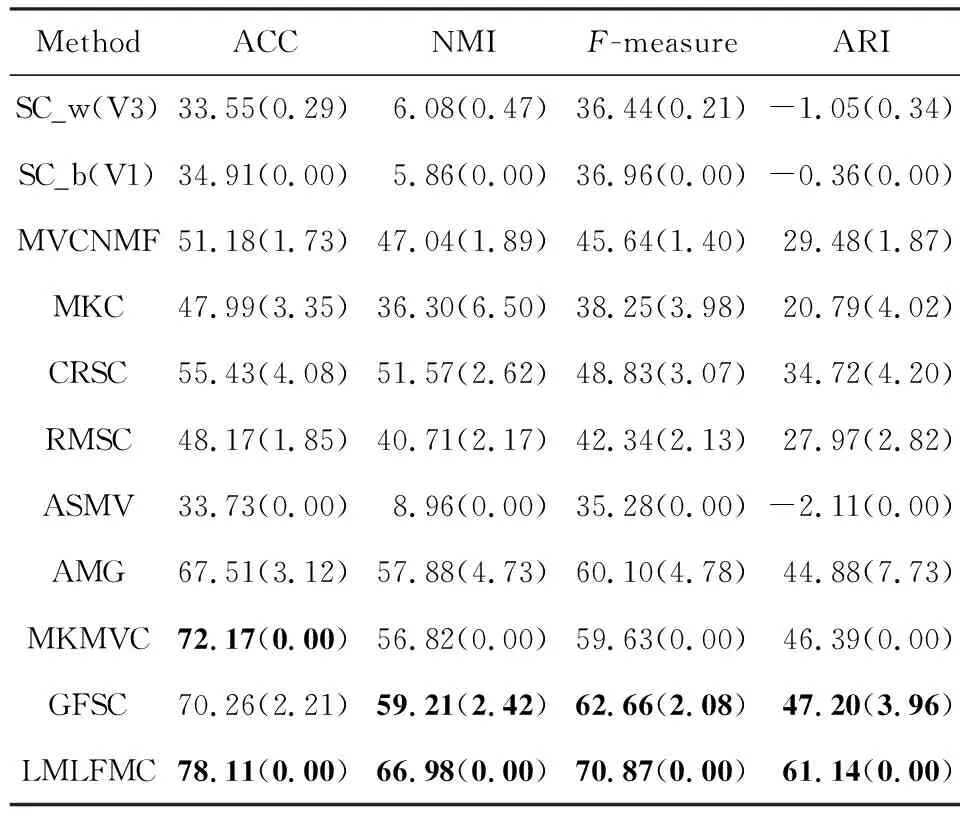
Table 2 Cluster Performance on 3sources Dataset表2 3sources数据集上的聚类性能

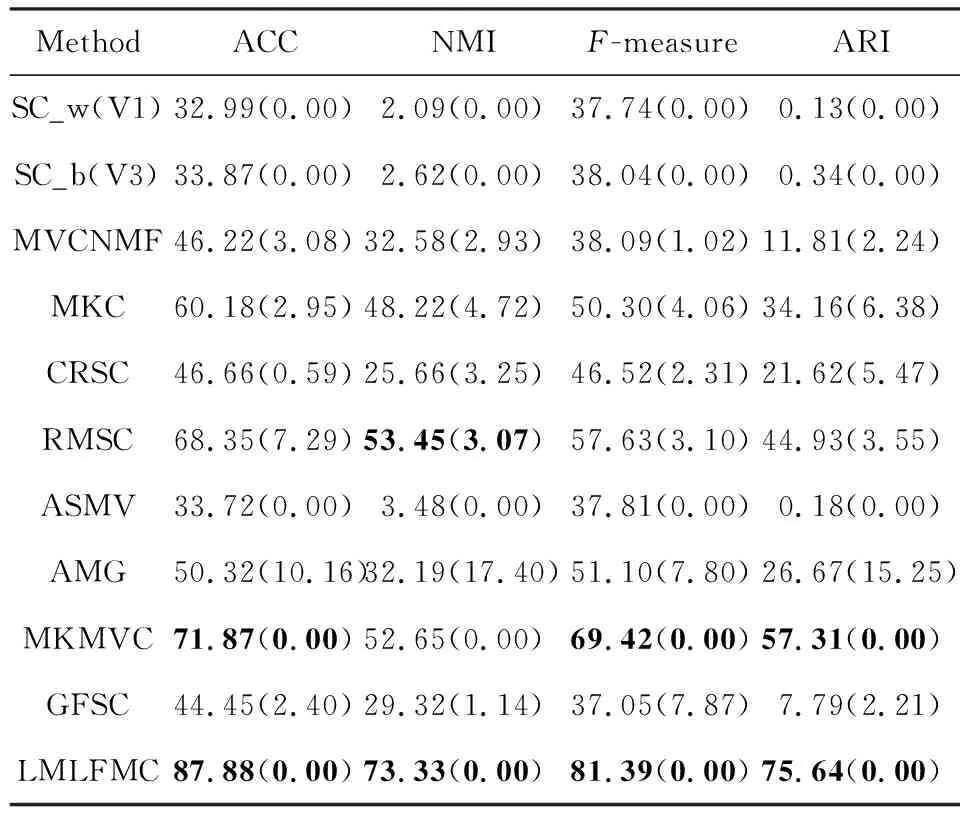
Table 3 Cluster Performance on BBC Dataset表3 BBC数据集上的聚类性能

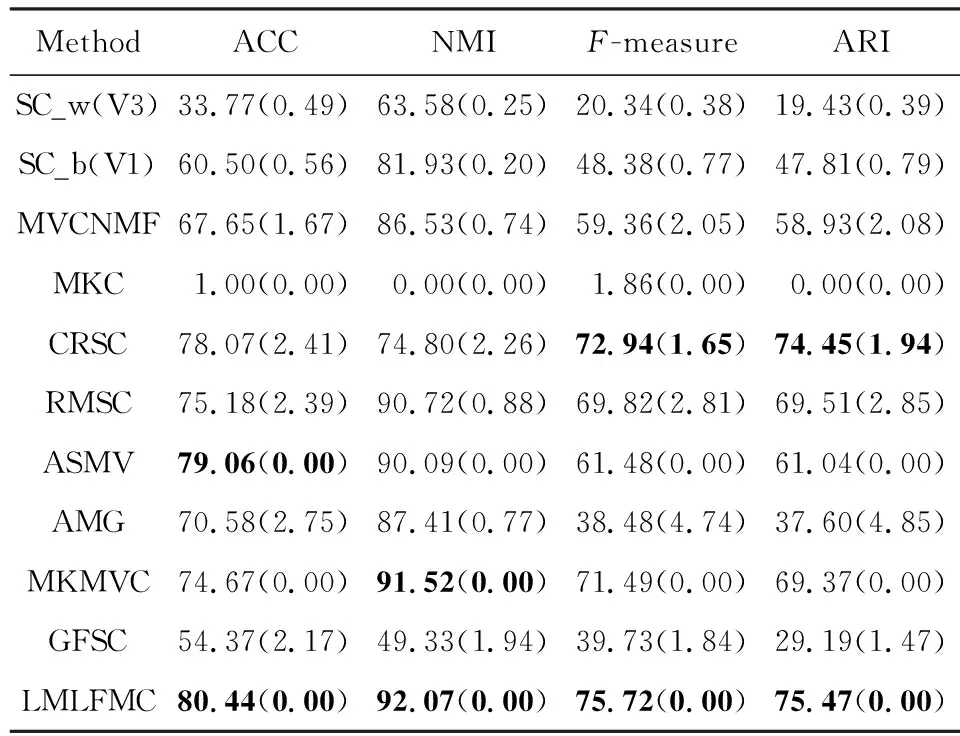
Table 4 Cluster Performance on 100leaves Dataset表4 100leaves数据集上的聚类性能

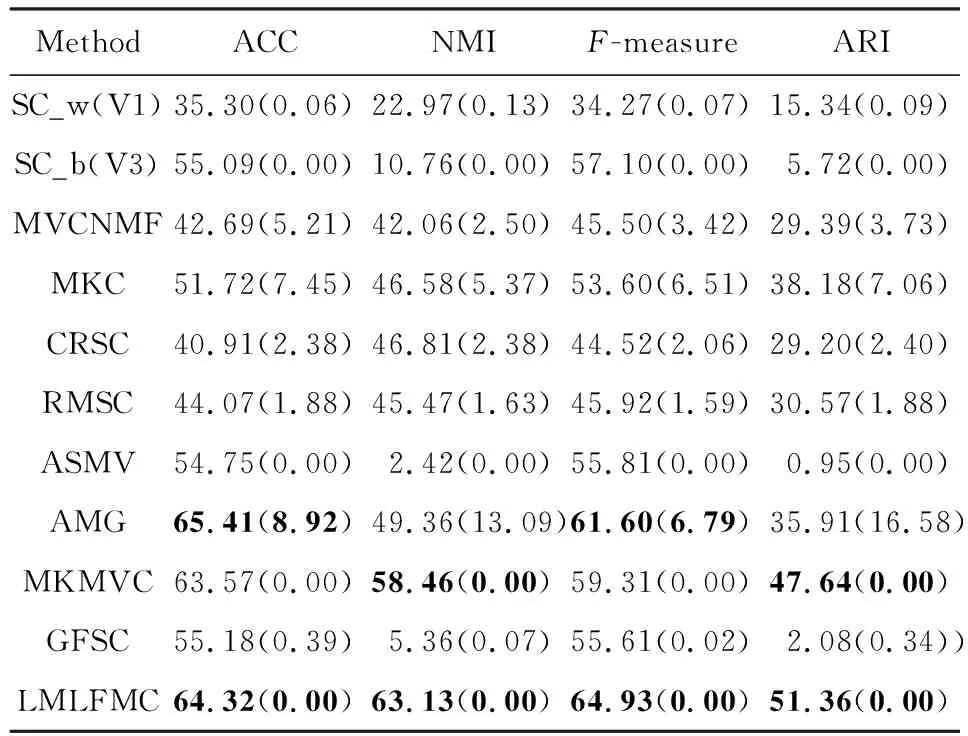
Table 5 Cluster Performance on Caltech101-7 Dataset表5 Caltech101-7数据集上的聚类性能

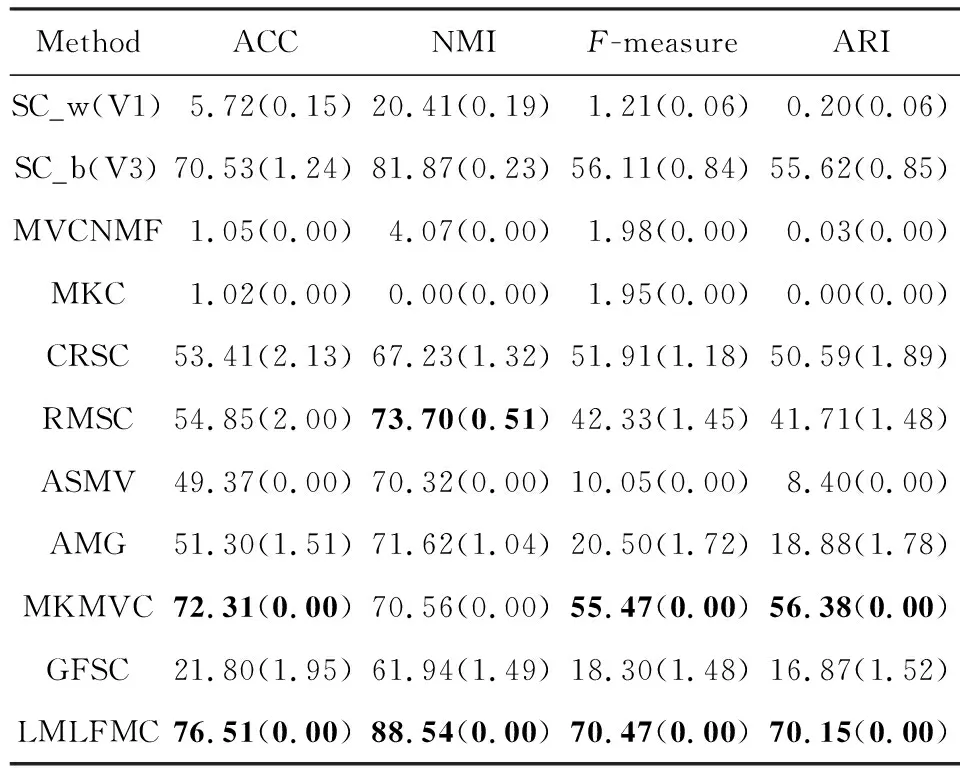
Table 6 Cluster Performance on ALOI Dataset表6 ALOI数据集上的聚类性能

Table 7 Cluster Performance on WebKB Dataset表7 WebKB数据集上的聚类性能

1) 聚类效果分析

① 除了Caltech101-7数据集上的ACC指标和WebKB数据集的NMI指标结果稍次，本文模型其他所有数据集的所有指标都比对比方法有显著提升.

② 从SC的结果可知，各视图的聚类性能差异显著.以ALOI为例，SC在V3视图上有较好效果，但在V1上的结果基本不可用.说明不同视图的数据相似图S差异较大，将它们强行融合不尽合理.采用类似融合方案的GFSC在ALOI上也效果不佳.

③ 包含附加的K-means聚类的算法，如SC，AMG，GFSC等，结果方差较大.AMG方法尤甚.而ASMV，MKMVC和本文算法由于不包含附加的K-means步骤，方差几乎为零.这说明消除附加的K-means聚类步骤可以提高稳定性.

④ 总体上，采用多核学习方案的MKMVC和本文方法在大部分数据集上都效果良好，说明多核学习能有效表征各个视图的数据点之间的非线性关系.而同样采用多核学习方案，本文的后融合方案显著优于MKMVC模型的相似图融合方案.

⑤ 某些情况下，单视图聚类得到的最佳结果偶尔优于部分多视图聚类算法，表明要充分利用多个视图之间的互补性和一致性并不容易，需仔细考量.

2) 时间性能分析

各种方法的运行时间如表8所示.其中SC_w(SC_b)分别记录了SC算法在相应数据集的聚类效果最差(最好)的单视图上运行10次的平均时间.由于SC算法在各个数据集上取得最佳或最差效果的单视图序号不一致，所以表8中SC_w(SC_b)省略了代表最差(最好)单视图序号(相应的序号可以从表2～7中查询).

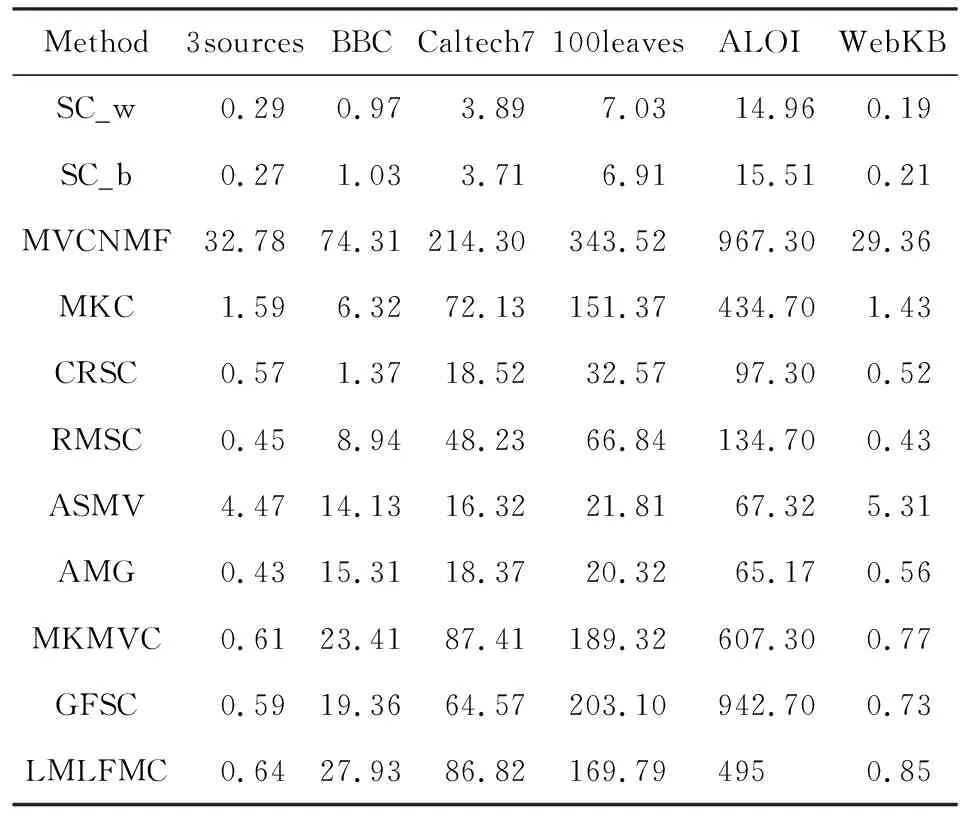
Table 8 Running Time of Each Method on All Dataset表8 各种方法在所有数据集上的运行时间 s

本文模型最耗时的环节是利用QPSM优化工具求解F.该计算过程时间的复杂度为O(n2ct)[31].其中n代表样本个数,c代表类别数，t为QPSM算法内部的迭代次数.

对样本个数多于1 000的数据集，所有算法都采用Matlab自带的GPU运算实现.从表8可知，基于多核学习的MKMVC算法和本文算法耗时都比较长，但考虑到聚类性能的显著提升，多核学习的时间代价依然是有价值的.但对比MKMVC算法和本文算法的运行时间可以看出，虽本文模型因包含QPSM子问题，理论上的时间复杂度高于MKMVC，但因采用邻域学习的方案，所以运行时间仍与MKMVC基本相当，甚至在较大的数据集上比MKMVC更快.这一点从AMG和GFSC的运行时间对比同样可看出，虽然两者的复杂度都为O(n3),但因AMG采用邻域学习方案，而GFSC采用全局自表达方案，所以AMG的运行时间显著少于GFSC.这些现象表明，邻域学习因需考虑的数据点较少，得到的相似矩阵也更为稀疏，可以显著提高运算速度.邻域学习的速度优势在样本较多的ALOI数据集上更加明显.

4.3 参数敏感性分析

本文算法包含3个参数(μ,α,λ).其中α在指定邻居个数k后，用附录A中的公式A(10)可直接求解，无需调参.以3source数据集为例，图1～4显示了当k=25时，各指标对不同参数设置的变化情况.

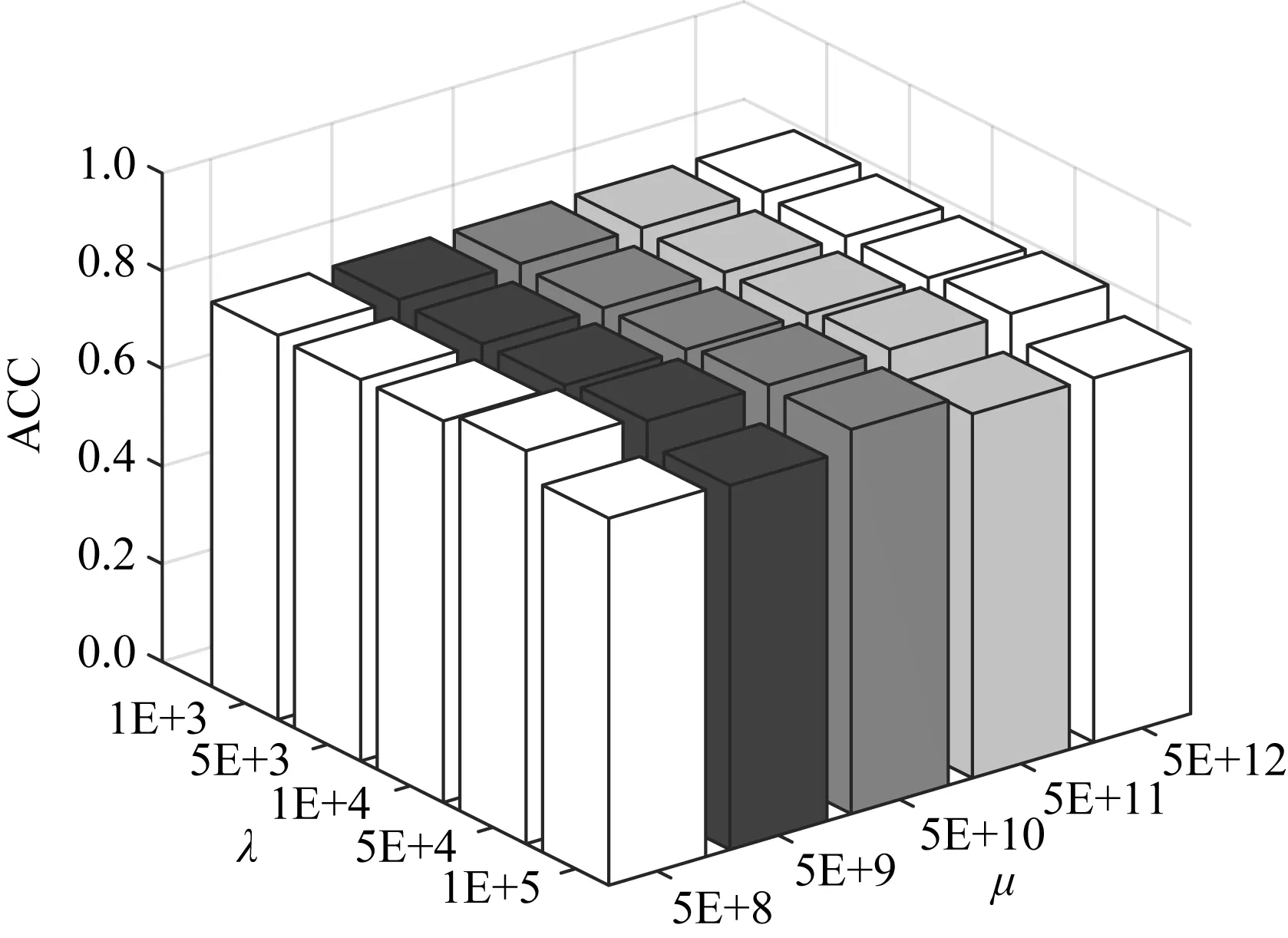
Fig. 1 ACC w.r.t. different parameter settingson 3sources图1 3sources数据集上不同参数设置时的ACC指标

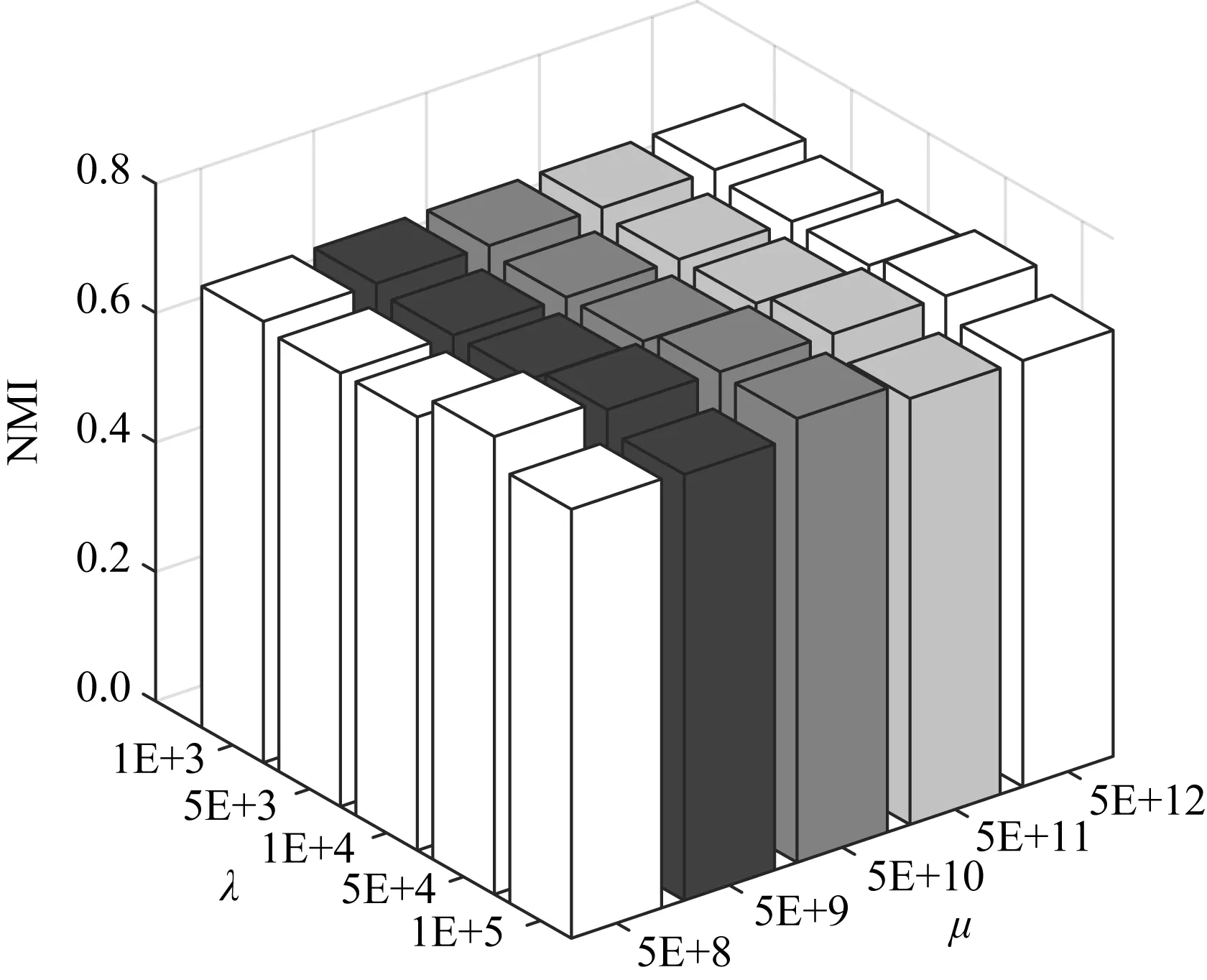
Fig. 2 NMI w.r.t. different parameter settingson 3sources图2 3sources数据集上不同参数设置时的NMI指标

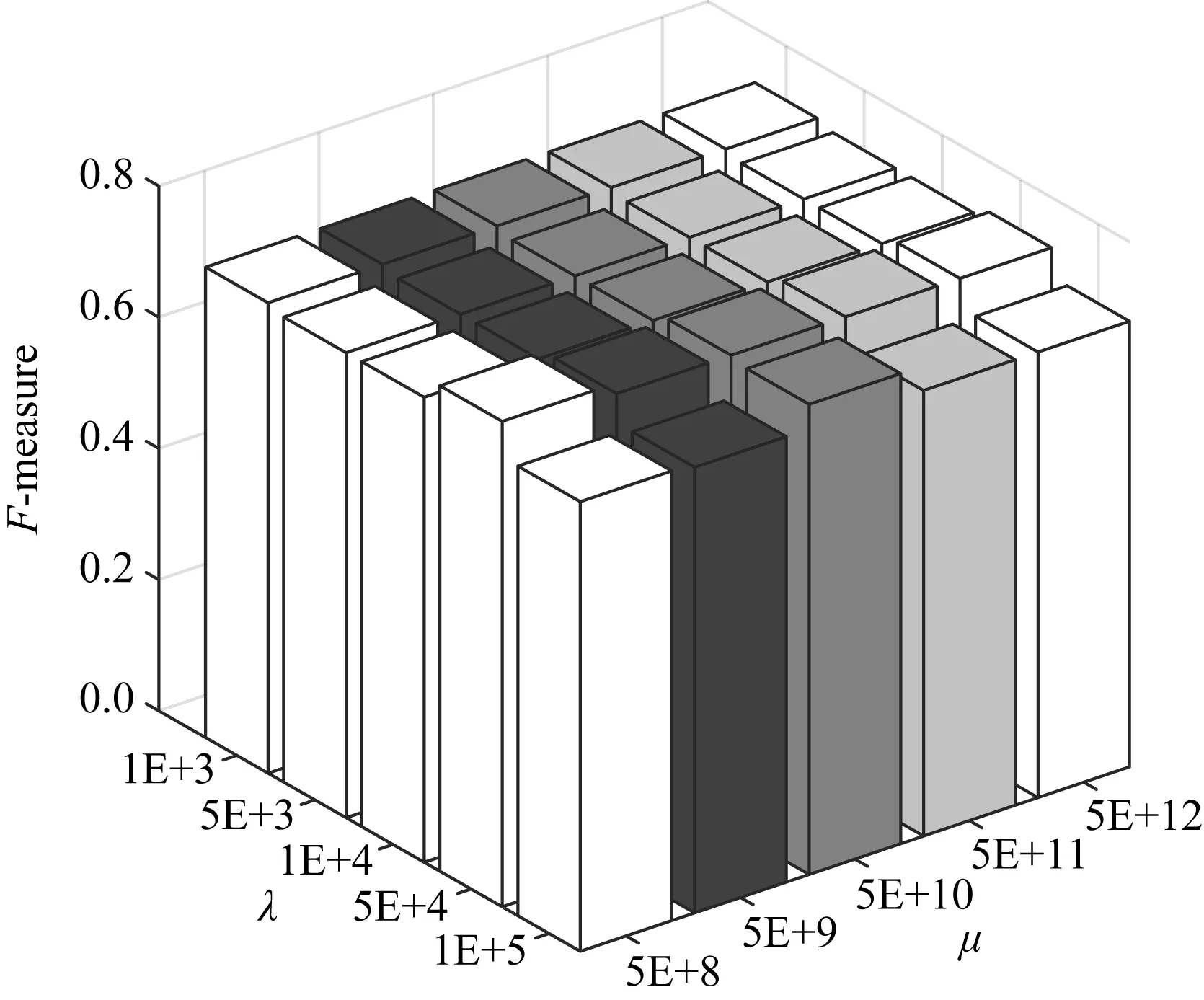
Fig. 3 F-measure w.r.t. different parameter settingson 3sources图3 3sources数据集上不同参数设置时的F-measure指标

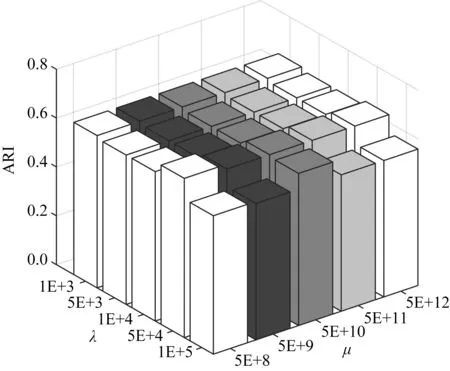
Fig. 4 ARI w.r.t. different parameter settingson 3sources图4 3sources数据集上不同参数设置时的ARI指标

从图1～4可以看出，本文算法对于参数μ和λ都不敏感.事实上，所有数据集μ取值{5E+8～5E+12}之间都能取得较好结果.算法对参数λ的稳定性稍次于λ，但当λ∈{1E+3,5E+3,1E+4,5E+4,1E+5}时，大部分数据集都能取得较好结果.表2～7所报导的性能指标，在所有数据集上的都设置为μ=5E+3,λ=5E+8.因此本文算法对于较大范围的参数设置是稳定的.

此外，与所有邻域方法类似，本文需指定邻居个数k.对所有邻域方法而言，最佳邻居个数k的确定目前仍是一个开放问题[27].但在本文模型中，对文本数据集取k≈25，对于图像数据集取k≈17时，都能取得较好结果.事实上，表2～7所示结果，3sources，BBC，WebKB上都取k=25，在Caltech101-7h和100leaves上取k=17，在ALOI上取k=19时获得.ALOI数据集取比另2个图像数据集稍多的邻居个数的原因在于，文献[27]给出的启发性建议指出，邻居个数应该与log(n)正相关.此外，通过观察文本数据集，发现其特征取值更为稀疏，数据集中特征取值存在大量为0的位置，因而需要考虑更多的邻居个数才能描述数据的局部非线性结构.总之，本文模型性能对于邻居个数k的取值是有规律可循的，是稳定的.

5 总 结

本文提出一种基于邻域多核学习的后融合多视图聚类算法.为充分挖掘数据间的非线性关系和减轻计算负荷，该算法采用邻域多核学习方案而不是全局核空间自表达模型.考虑到不同视图的相似图之间的聚类性能差异，本文在类别指示矩阵层次而不是数据相似图的层次进行信息融合.最后，本文提出一种交替优化方案，将相似图的构建和聚类生成等子任务进行协同优化，从而避免所构建的相似图对于聚类任务并非最优.实验结果表明:本文算法的聚类性能优于若干现有的多视图聚类算法.