关于非参数统计中几种双样本位置参数检验方法的分析
2020-08-24曹淑娟李佳泽
曹淑娟, 李佳泽, 周 晨
(天津工业大学 数学科学学院,天津 西青 300387)
0 引言
非参数统计是统计学的一个重要分支,是21世纪统计理论的重要发展方向之一。传统的参数方法强烈依赖于对总体分布的假设,而非参数统计与总体分布几乎没有什么关系,不用假定特定的总体分布,仅需要一些非常一般性的假设(例如连续分布、对称分布等),利用样本观察值中一些比较直观的信息进行统计推断,有许多学者和教师在教学和研究中都提到非参数统计的这一特点,并利用非参数统计解决具体的问题[1-2]。也因为如此,非参数统计成为一门应用性和研究性兼具的核心课程[3]。
在实际问题中,常常需要比较两个总体的位置参数,如两种市场营销策略哪种更有效,两种汽油哪一种对环境的污染更少,两种训练方法哪一种更出色等,如果总体的分布未知,就需要用到非参数统计中的两样本位置参数的检验方法了。笔者根据文献[4-6]总结了4种两样本位置参数检验方法:符号检验、Brown-Mood中位数检验、Wilcoxon秩和检验和Wilcoxon-Mann-Whitney检验,针对不同的假设检验问题,选择不同的检验统计量,以表格的形式简洁地描述了不同的拒绝域的具体形式和求p值的方法。最后分别用这4种检验方法解决一个实际问题。
1 非参数统计中两样本位置参数检验
1.1 符号检验[4,6]
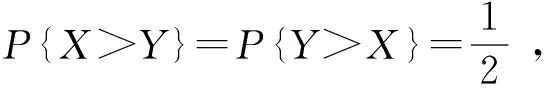


表1 符号检验的基本内容Tab.1 Basic content of sign test
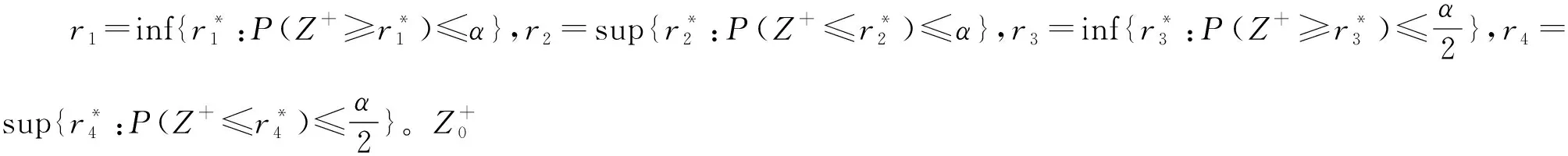
当样本量n足够大(>10)时,由棣莫佛-拉普拉斯中心极限定理可知
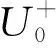

表2 符号检验大样本的基本内容
1.2 Brown-Mood中位数检验[5]
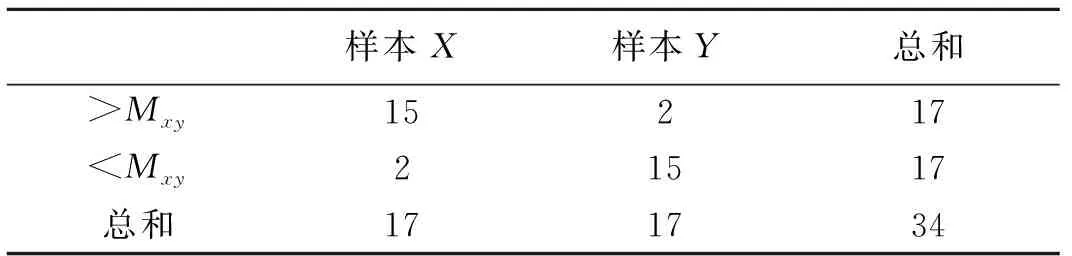
假设X1,X2,…,Xm;Y1,Y2,…,Yn是两组相互独立的样本,来自两个分布F(x)和F(x-μ),有相应的中位数mex和mey。假设检验问题为H0:mex=mey。在原假设成立的情况下,如果两组数据有相同的中位数,则将两组数据混合后,两组数据的混合中位数mexy与mex相等,两组数据应该比较均匀分布在mexy两边。因此,与符号检验类似,检验的第一步是找出混合数据的样本中位数Mxy,将X和Y按照分布在Mxy的左右两侧分为4类,对每一类计数,形成四格表如表3。

表3 Brown-Mood中位数检验的四格表
令A,B,C,D表示表3中4个类别的样本点数,A表示X样本中大于Mxy的个数。t表示混合样本中大于Mxy的个数,它依赖于m+n的奇偶性,当m,n和t固定后,A的分布在原假设下服从超几何分布A~H(t,m,N),其概率的计算公式为
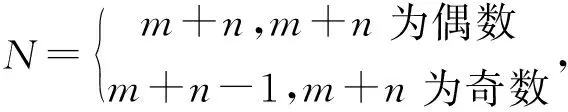

表4 Brown-Mood中位数检验的基本内容
注意:两样本数据混合之后排秩,找出中位数Mxy后,如果样本数据中存在与中位数一致的样本数据,应该删除。
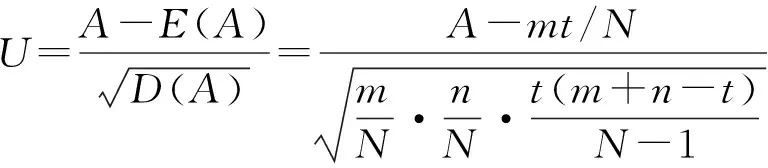

表5 Brown-Mood中位数检验大样本的基本内容
1.3 Wilcoxon秩和检验[5-6]
Wilcoxon秩和检验是Wilcoxon于1945年提出的,在应用上有重要意义。它的提出,极大地推动了有关秩的方法的发展。假设X1,X2,…,Xm;Y1,Y2,…,Yn是两组相互独立的样本,来自两个分布F(x)和F(x-μ),同Brown-Mood中位数检验法一样,可以分别记X和Y的中位数mex和mey。在mex>mey时,认为X1,X2,…,Xm和Y1,Y2,…,Yn混合之后,从小到大排秩,Y样本Y1,Y2,…,Yn倾向排在前面,而mex 表6 Wilcoxon秩和检验的基本内容 表7 Wilcoxon秩和检验大样本的基本内容 Wilcoxon-Mann-Whitney检验是Mann和Whitney于1947年提出的,是Wilcoxon秩和检验的推广,但是与Wilcoxon秩和检验区别不大。Wilcoxon-Mann-Whitney检验统计量表示混合样本中X观测值小于Y观测值的个数,表达式为 其中,ri=#{xi 与Wxy相对应的,有 其中,rj=#{xi>yj,i=1,2,…,m},j=1,2,…,n。显然,Wxy+Wyx=mn。 有关国内南北方34座主要城市的年平均气温差异研究。数据来源于2017年中国统计年鉴“国内南北方划分主要依据秦岭—淮河一线及其延长线”[7],数据如表8和表9。在对国内南北方的年平均气温差异研究中,收集了国内34座主要城市2017年度的年平均气温数据,用来研究南北地区的年平均气温是否存在显著差异(在对总体不作任何分布假设的前提下)。 表8 2017年南方城市的年平均气温/℃ 表9 2017年北方城市的年平均气温/℃ 设国内南方城市平均气温的中位数为mex;国内北方城市平均气温的中位数为mey。建立问题:原假设H0:mex=mey;备择假设H1:mex>mey,显著性水平α=0.05。 针对上面检验问题,计算检验统计量的实验值,Z+=17;即当显著性水平α=0.05时,拒绝域为w={Z+>12}。检验统计量Z+落入拒绝域中,所以拒绝原假设。或计算p值:p(b(N,1/2)≥Z+),算得p值为0,远远小于α=0.05,所以拒绝原假设,接受备择假设。认为在2017年国内南方城市年平均气温显著高于北方城市年平均气温。 对南北城市的平均气温混合排秩,如表10,其中南方城市的样本数据个数为17,[]中是北方城市的17个样本数据。 表10 南北城市的平均气温混合秩 计算混合样本中的中位数mexy=15.65,国内南方城市中平均温度低于混合样本的中位数的个数2;高于混合样本中位数的个数15,国内北方城市中平均温度低于混合样本的中位数的个数15;高于混合样本中位数的个数2;四格表如表11。 表11 气温比较四格表 计算p值近似为0,小于α=0.05,所以拒绝原假设,接受备择假设。认为在2017年国内南方城市年平均气温显著高于北方城市年平均气温。 如同Brown-Mood中位数检验法的实例分析,Wilcoxon秩和检验要对南北城市的平均气温混合排秩,求出秩和 Wx=427.5,Wy=167.5。 选取Wy作为检验统计量。由于数值较大,查表无法实现,可以考虑基于大样本下的Wilcoxon 秩和检验的渐进正态分布,在此不详述。因为Wilcoxon 秩和检验和Wilcoxon-Mann-Whitney检验完全等价,Wilcoxon-Mann-Whitney检验是Wilcoxon秩和检验的推广,因此用Wilcoxon-Mann-Whitney检验即可。 Wilcoxon-Mann-Whitney检验也得先对南北城市的平均气温混合排秩,选取检验统计量 得到检验统计量的实验值Wyx=Wx-m(m+1)/2=274.5。 当m=17,n=17,算得p值4.07E-06远小于α=0.05,所以拒绝原假设,接受备择假设。认为在2017年国内南方城市年平均气温显著高于北方城市。 非参数统计常用的两样本位置参数检验方法有符号检验、Brown-Mood中位数检验法、Wilcoxon秩和检验以及它的推广Wilcoxon-Mann-Whitney检验等。 符号检验是非参数统计中很古老的检验法,主要是利用正、负号的数目对某种假设做出推断。优点是简单方便,并不要求知道被检验量的分布规律,所以用途十分广泛。符号检验法只考虑了正、负号的个数,而没有考虑到数据大小的信息,这就导致了数据信息有所损失,精确度不高。当两样本的样本容量相差较大的时候,需要舍弃较多的数据,数据信息损失更多,符号检验法适用于两样本的数据量一致的情况。 Brown-Mood中位数检验的主要思想是将两样本混合起来排秩,将两样本中大于或小于混合样本中位数的数据个数进行计数,绘制四格表,利用超几何分布进行检验。 Wilcoxon秩和检验主要对两样本数据混合排秩,并计算秩和检验统计量进行检验。当样本数据量较大时,统计量值太大不易处理,可用其统计量的渐近分布解决,或用其推广的方法——Wilcoxon-Mann-Whitney检验法,这两种方法本质上是等价的,一般采用后者进行检验。当样本数据充分大的时候,考虑基于大样本下的渐近正态分布,利用正态分布进行显著性检验。这两种方法既考虑了数据的符号,又考虑了数据大小信息,较符号检验更为全面考虑数据的相关信息。 这些非参数检验方法的共同优点是,不知总体分布的时候也可以使用,但是它们有一个共同的缺点,即,当数据符合参数检验条件时,这些非参数检验没有充分运用数据信息。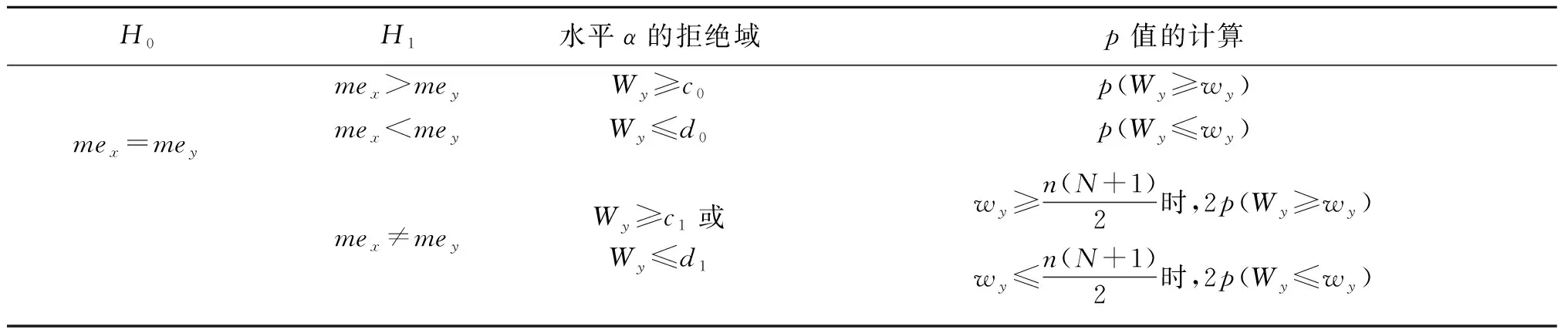
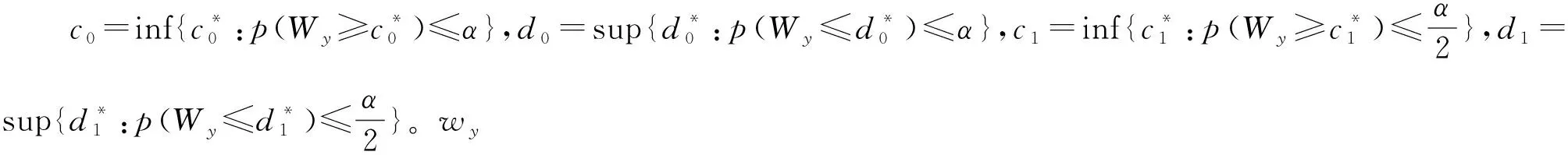

1.4 Wilcoxon-Mann-Whitney 检验[5-6]
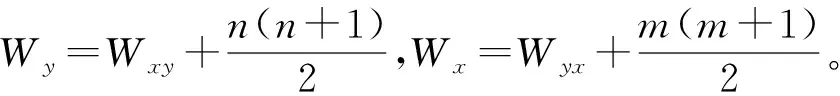
2 实例分析


2.1 符号检验法的实例分析
2.2 Brown-Mood中位数检验法的实例分析
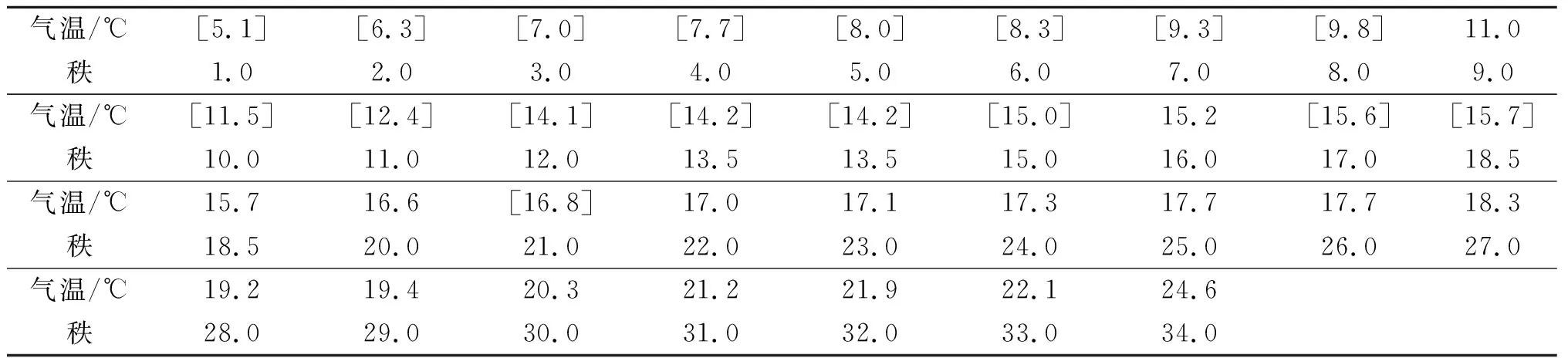
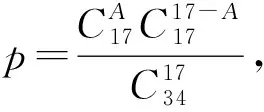
2.3 Wilcoxon秩和检验和Wilcoxon-Mann-Whitney检验的实例分析
3 结束语
