利用无理函数变换构造新的无穷级数恒等式

张来萍

(宁夏大学 新华学院,宁夏 银川 750021)

0 引言

无穷级数变换有许多研究，文献[1]收录了1 000多级数公式，文献[2]介绍了无穷级数求和的各种技术，文献[3-5]讨论了组合数和式问题，文献[6-10]用裂项法给出了中心型和非中心型二项式系数倒数级数封闭型和式问题。无穷级数与数学各个分支联系紧密，也可以说，无穷级数与数学各个分支已经融合在一起。因此研究无穷级数时常常利用微积分、伽马贝塔函数、多对数、发生函数和递推关系等各种数学工具和方法。

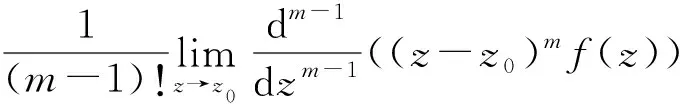
1 引理[14]

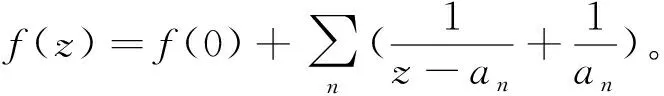
2 主要结果与证明

命题1无穷级数恒等式成立

(1)

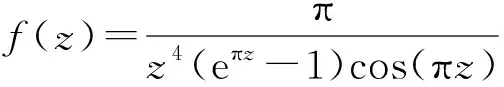
1)把f(z)函数展开成幂级数

(πz/2+(πz)2/6+(πz)3/24)2-(πz/2+(πz)2/6)3+(πz/2)4+…)=

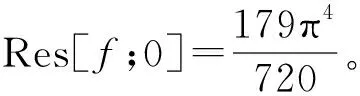
2)在单极点z=±2ni，用洛必达法则计算f(z)的留数，

3)在单极点z=±(2n+1)/2，计算f(z)的留数

根据留数基本定理“函数在扩充复平面内所有奇点留数总和必等于零”[9]的结论，有

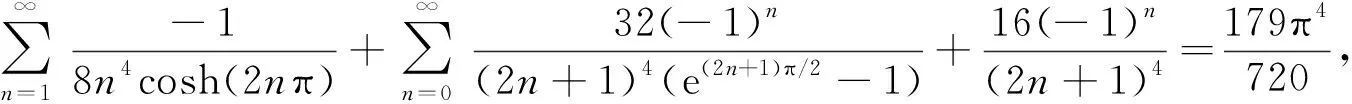
命题2无穷级数恒等式

(2)

成立。

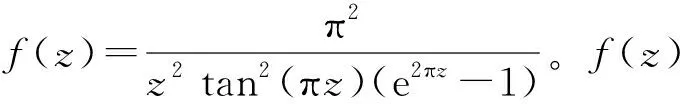
把f(z)展开成幂级数

(πz+2(πz)2/3+(πz)3/8)2-(πz+2(πz)2/3)3+(πz)4+…)=

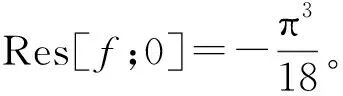
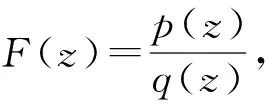
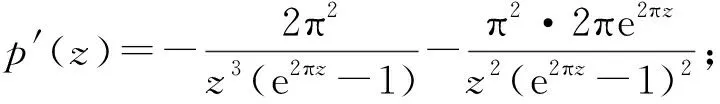
q′(z)=2πtan(πz)sec2(πz)；q″(z)=2π2sec4(πz)+4π2tan2(πz)sec(πz)；

q‴(z)=8π3sec4(πz)tan(πz)+8π3tan(πz)sec3(πz)+4π3tan3(πz)sec(πz)；

q″(n)=2π2sec4(nz)=2π2；q‴(n)=0。

将上述数据代入公式可得

在单极点z=ni,n≠0，使用洛必达法则计算f(z)留数，

根据留数基本定理“函数在扩充复平面内所有奇点留数总和必等于零”[11]，从而有

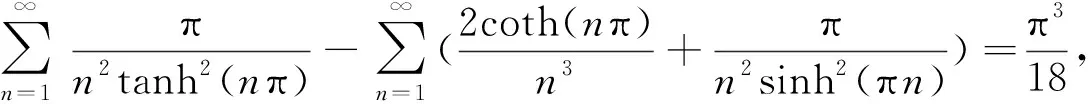
命题3设α,β>0,且αβ=π2, 则无穷级数变换

(3)

成立。

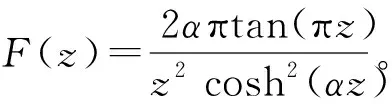
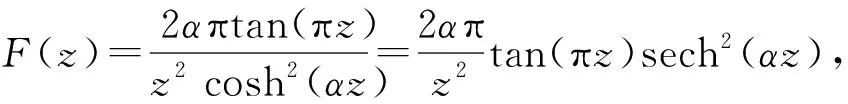
函数F(z)展开成幂级数z-1的系数，即为F(z)在z=0时的留数，Res[F(z);0]=2απ2。

2)在单极点z=(2k+1)/2，计算F(z)的留数得

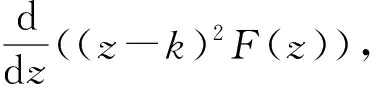
p(πi(k+1/2)/α)=2παtan(π2(k+1/2)i/α)=2παitanh(π2(k+1/2)/α)=2παitanh(β(2k+1)/2)；

p′(πi(k+1/2)/α)=2π2αsech2(β(2k+1)/2)。

下面计算q(z)的导数，

q′(z)=2zcosh2(αz)+2z2αcosh(αz)sinh(αz)=2zcosh2(αz)+z2αsinh(2αz)；

q″(z)=2cosh2(αz)+4zαcosh(αz)sinh(αz)+2zαsinh(2αz)+2z2α2cosh(2αz)=

2cosh2(αz)+4zαsinh(2αz)+2z2α2cosh(2αz)；

q‴(z)=2sinh(2αz)+4αsinh(2αz)+8zα2cosh(2αz)+4zα2cosh(2αz)+4z2α3sinh(2αz)=

(2+4α+4z2α3)sinh(2αz)+12zα2cosh(2αz),

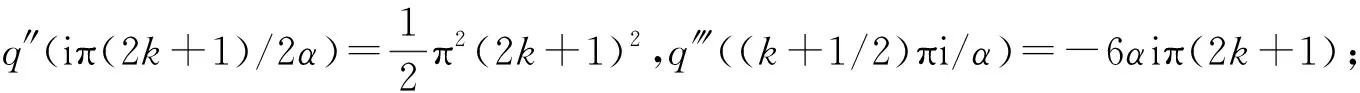
根据留数基本定理“如果函数F(z)在扩充复平面内只有有限个奇点，那么f(z)在所有奇点(包括∞点)的留数总和必等于零”[11]，于是有

即

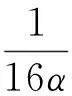
故(3)式成立。

命题4设α,β>0,且αβ=π2无穷级数恒等式

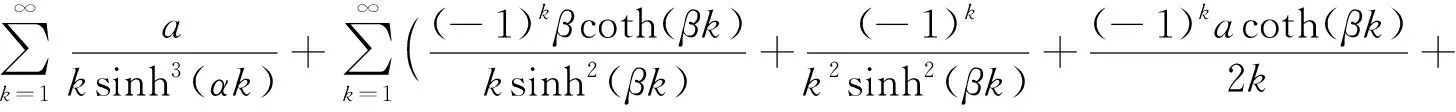
(4)

成立。

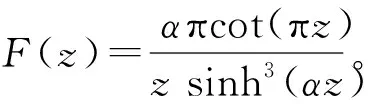
1)把F(z)展开成幂级数，即

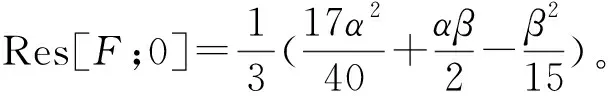
2)在单极点z=k，计算F(z)的留数

2) 配置连接核心交换机CS6509的端口属性Switch Port Configuration→Port Groping Parameters,设置所属的端口组为student1,启用端口聚合协议PAgP(Port Aggregation Protocol),端口模式采用desirable模式[15]．

令p(z)=παcot(πz)，q(z)=zsinh3(αz)，则p′(z)=-απ2csc2(πz)，p″(z)=2απ3csc2(πz)cot(πz)，于是有导数值

p(iπk/α)=-παicoth(βk)，

p′(iπk/α)=-απ2csc2(π2ki/α)=-απ2csc2(βki)=απ2csch2(βk)，

p″(iπk/α)=2απ3csc2(π2ik/α)cot(π2ik/α)=2απ3icsch2(βk)coth(βk)。

计算q(z)=zsinh3(αz)，q′(z)=sinh3(αz)+3zαsinh2(αz)cosh(αz)，

q″(z)=3αsinh2(αz)cosh(αz)+3αsinh2(αz)cosh(αz)+6zα2sinh(αz)cosh2(αz)+3zα2sinh3(αz)=

6αsinh2(αz)cosh(αz)+6zα2sinh(αz)cosh2(αz)+3zα2sinh3(αz)，

q‴(z)=12α2sinh(αz)cosh2(αz)+6α2sinh3(αz)+6α2sinh(αz)cosh2(αz)+

6zα3cosh3(αz)+12zαsinh2(αz)cosh(αz)+9zα3sinh2(αz)cosh(αz)=

18α2sinh(αz)cosh2(αz)+21zα3sinh2(αz)cosh(αz)+6α2sinh3(αz)+6zα3cosh3(αz)，

q(4)(z)=18α3cosh3(αz)+36α3sinh2(αz)cosh(αz)+21α3sinh2(αz)cosh(αz)+

42zα4sinh(αz)cosh2(αz)+21zα3sinh3(αz)+18α3sinh2(αz)cosh(αz)+

6α3cosh3(αz)+18zα4sinh(αz)cosh2(αz)=

24α3cosh3(αz)+75α3sinh2(αz)cosh(αz)+60zα4sinh(αz)cosh2(αz)，

q(5)(z)=72α4sinh2(αz)cosh(αz)+150α4sinh(αz)cosh2(αz)+75α4sinh3(αz)+

60α4sinh(αz)cosh2(αz)+60zα5cosh3(αz)+120zα5sinh2(αz)cosh(αz)。

于是有导数值q‴(iπk/α)=6(ikπ/α)α3(-1)k=6(-1)kπα2ki，

q(4)(iπk/α)=24(-1)kα3，q(5)(iπk/α)=60(ikπ/α)α5(-1)k=60(-1)kπα4ki，

p(iπk/α)=-παicoth(βk)，p′(iπk/α)=απ2csch2(βk)，

p″(iπk/a)==2απ3icsch2(βk)coth(βk)。

将数值代入留数计算公式可得

Res[F;iπk/α]=3(2απ3icsch2(βk)coth(βk))/(6(-1)kπα2ki)-

3(απ2csch2(βk))(24(-1)kα3)/2(6(-1)kπα2ki)2-

3(-παicoth(βk))(60(-1)kπα4ki)/10(6(-1)kπα2ki)2+

+3(-παicoth(βk))(24(-1)kα3)2/8(6(-1)kπα2ki)3=

根据留数基本定理中“函数在扩充复平面内所有奇点留数总和必等于零”的结论[11]，有

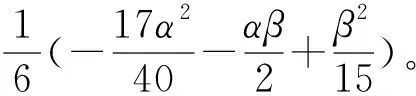
命题5无穷级数恒等式成立

(5)

(6)

其中χ(k)表示模4非本原特征，即χ(2k)=0，χ(2k+1)=(-1)k。

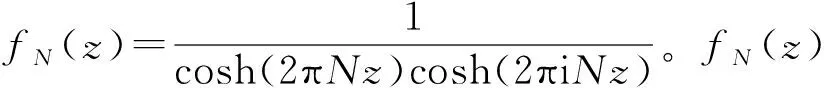
1)在单极点z=i(2k+1)/(4N)，用洛必达法则计算fN(z)的留数,

在单极点z=±i(2k+1)/(4N)，函数fN(z)展开式

(7)

2)在单极点z=±(2k+1)/(4N)，用洛必达法则计算fN(z)的留数，

(8)

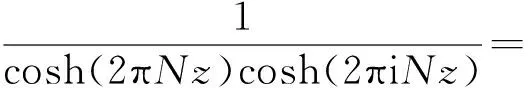
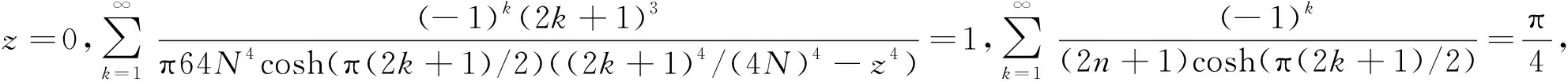
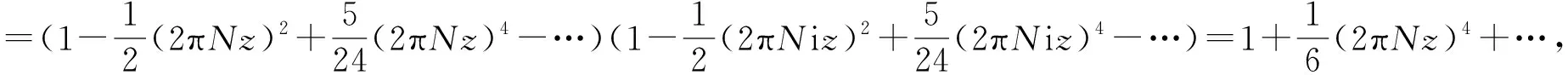
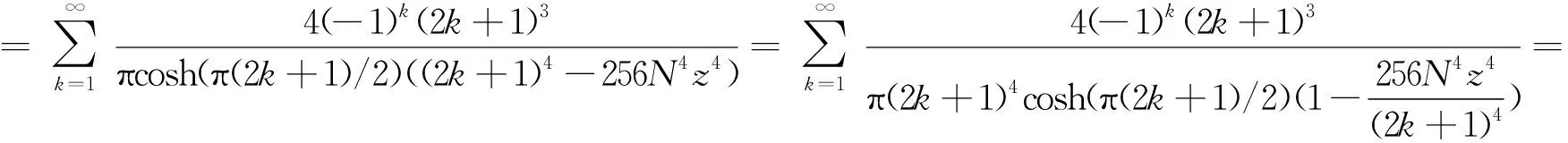
比较两端z4系数,可得

故(6)式成立。