基于伪随机线性调频的双序列跳频通信系统*
2020-08-22唐志强全厚德孙慧贤崔佩璋
唐志强,全厚德,孙慧贤,2,崔佩璋
(1.陆军工程大学石家庄校区,石家庄 050003;2.电子科技大学通信抗干扰国家级重点实验室,成都 611731)
0 引言
跳频技术因其良好的抗干扰性能广泛应用于军事通信领域[1]。随着干扰技术的进步,FH/BFSK在跟踪干扰下通信性能迅速恶化[2]。虽然提高跳速可以更好地对抗干扰,但是硬件对跳速会有限制[3]。差分跳频(Differential Frequency Hopping,DFH)具有很强的抗跟踪干扰能力,但是却存在误码扩散的缺点[4],而且一般采用宽带接收,不利于接收端滤除干扰信号,抗部分频带干扰性能较差[5]。传统的跳频技术存在各自的缺点,近年来,许多新的技术手段被用来提升跳频系统的抗干扰性能。文献[6]利用混合信道下优化的LDPC 编码技术对跳频系统进行了改进,获得了0.62 dB 的性能增益。文献[7]将博弈理论运用到跳频通信中,并在线性约束条件下推导出了纳什平衡的充分必要条件。文献[8]利用OAM 的正交性实现抗干扰,研发的MFH 跳频模式误码率远小于传统跳频方案。双序列跳频(BSFH)是另一种新型的跳频通信方法,兼具较好的抗跟踪干扰和部分频带干扰性能[9-10],但是当BSFH 的对偶信道被干扰时,误码率急剧增加。文献[11]将FRFT和跳频技术相结合,有效提高了系统的抗截获性能。针对BSFH 的致命弱点,提出了伪随机线性调频的双序列跳频(Pseudo Randomlinear Frequency Modulation Binary-Sequence Frequency Hopping,PRLFM_BSFH)通信系统。并对其抗窄带跟踪干扰和部分频带干扰性能做了分析。通过与BSFH 和FH/BFSK 做对比,全面体现出改进方法所带来的性能增益。
1 系统模型
PRLFM_BSFH 系统模型主要由双序列跳频模块、伪随机线性调频模块和分数阶傅里叶处理模块3 大部分组成。其原理框图如图1 和图2 所示。
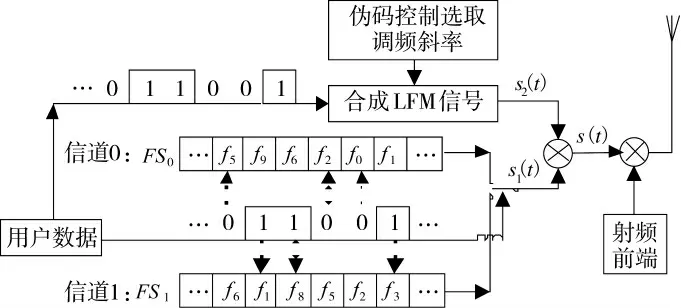
图1 PRLFM_BSFH 通信系统发射机原理框图
1.1 双序列跳频模块
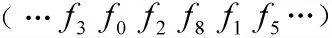
图2 PRLFM_BSFH 通信系统接收机原理框图
BSFH 模块产生的跳频信号可以表示为:
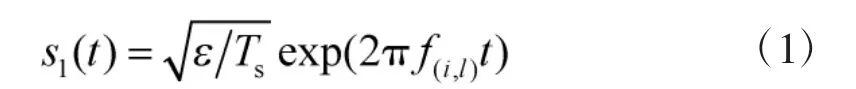
其中,i 等于0 或者1,表示信道0 或者信道1,l 表示当前发送的是第l 跳信号。ε 表示比特能量,表示跳速和信息速率相等。
传统的BSFH 接收机采用能量检测,这使得BSFH 具有较好的综合抗干扰能力。图2 是BSFH的抗干扰原理图。
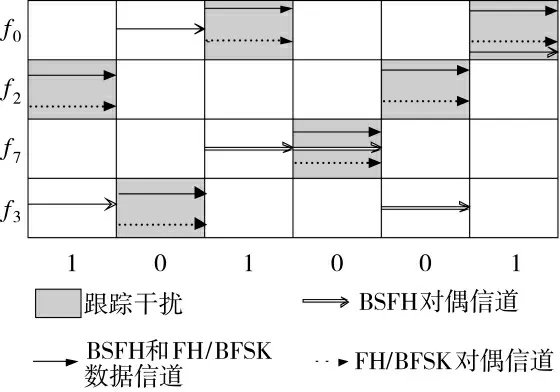
图3 BSFH 抗干扰原理图
从上图中可以看出FH/BFSK 对偶信道和数据信道间隔固定,干扰可以同时覆盖,而BSFH 采用双序列跳频,干扰很难同时覆盖。当跟踪干扰影响BSFH 数据信道时,由于接受端采用能量检测,干扰反而会增大检测概率。但是在图中的第4 跳和第6跳可以发现,当BSFH 的对偶信道被干扰时,接收端依然采用能量检测就很容易出现误码,这也是BSFH 的致命之处。基于以上分析,提出了PRLFM_BSFH 通信方法对此进行改进,此方法在每一跳混频一个LFM 信号作为特征信息来提高信号检出概率,而接收端进行分数阶傅里叶变换后采用抽样比值判决得到发端信息。下面分别对这两个模块进行介绍。
1.2 伪随机线性调频模块
该模块产生的LFM 信号可以表示为[9]:

其中,uk为调频斜率。由伪码控制将每一比特信息码元用具有不同调频斜率的LFM 信号代替,由于合成的LFM 信号的uk在伪随机地变化,故称之为伪随机线性调频信号。然后将LFM 信号与跳频信号进行混频,便可以得到待发送的PRLFM_BSFH信号s(t)。
1.3 分数阶傅里叶变换处理模块
接收端把接收到的信号首先进行解跳处理,然后采用分数阶傅里叶变换判断哪一个信道存在特征信息。傅里叶变换可以看成是将信号从时间轴逆时针旋转π/2 到频率轴的算子,而分数阶傅里叶变换可以看成是旋转任意角度α 的算子。对于发射信号s(t)的分数阶傅里叶变换可以表示为[10]:

可以事先计算出每段LFM 信号峰值位置对应的uk,然后在同步的前提下,接收信道0 和1 分别在每个信息码元周期内在事先存好的峰值位置处进行采样,比大输出,得到发端信息。
2 性能分析
在理论推导过程中所使用的信道为AWGN 信道。假设跟踪干扰波形为高斯窄带噪声,其可以影响到对偶信道。为了重点考察干扰对系统性能的影响,故忽略热噪声。
2.1 跟踪干扰下的误码率
接收端信号r(t)经过解跳带通滤波后可由下式表示:

由以上分析可知,r1(t)服从高斯分布,由于FRFT 是线性变换,所以对信号做pk阶的FRFT 可以看成是信号通过一个线性滤波器。而高斯过程通过线性系统后仍然服从高斯分布。对于复高斯过程经过模平方变换后服从自由度为2 的卡方分布。
假设当前跳用户信息占用信道1,则在跟踪干扰成功时,其抽样值ξ1服从自由度为2 的非中心卡方分布,均值的平方和定义为a2,其值由式(5)给出。ξ1的概率密度函数由下式给出:

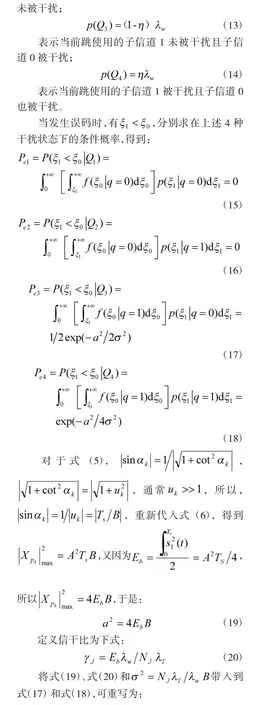

2.2 部分频带干扰下的误码率

3 数值和仿真结果分析

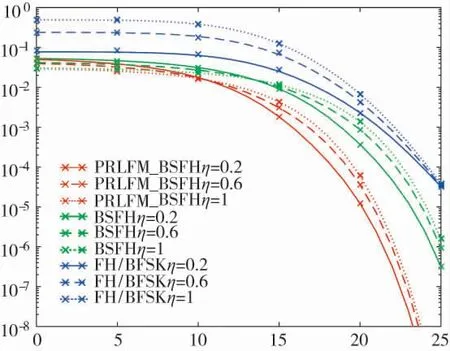
图4 PRLFM_BSFH、BSFH、FH/BFSK 在不同跟踪干扰成功率η 下的性能
图5 分析了跟踪干扰时间比例对3 种通信系统的性能影响。参数η=1=1/16。由图可知,随着干扰时间比例增加,3 种系统的性能都出现了一定的恶化。在相同条件下,PRLFM_BSFH 比FHBFSK约有5 dB 的性能增益,PRLFM_BSFH 平均比BSFH大约有4 dB 的性能增益,性能的提升也是由于特征信息提高了信号检出概率。
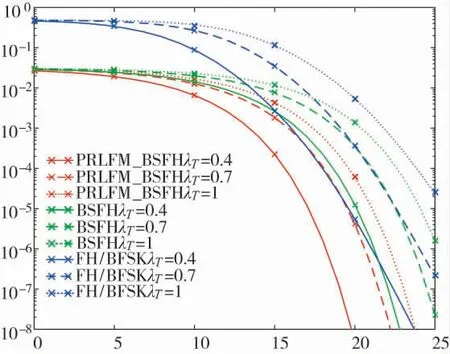
图5 PRLFM_BSFH、BSFH、FH/BFSK 在不同跟踪干扰时间比例下的性能
图6 是3 种通信系统在不同跟踪干扰带宽比例下的误码率曲线对比图。参数η=1。FHBFSK随着干扰带宽增加,误码率降低。对于PRLFM_BSFH 和BSFH 来说,信干比一定时,存在最佳干扰带宽比例,使得两种通信系统的误码率达到最大。当小信干比时,最坏跟踪干扰的带宽应当大一些,这样可以更大概率干扰到对偶信道而产生误码;当信干比较大时,最坏跟踪干扰的带宽应当小一些,这是由于信号能量足够大,只有将干扰功率集中,当干扰到对偶信道时,才可以产生误码。在相同条件下,PRLFM_BSFH 比FHBFSK 约有10 dB 的性能增益,比BSFH 约有4 dB 的性能增益。

图6 PRLFM_BSFH、BSFH、FH/BFSK在不同跟踪带宽比例下的性能
图7 是3 种通信系统在最坏跟踪干扰下的误码率曲线。参数1。选择不同的跟踪干扰成功率和干扰带宽比例,使得系统的误码率达到最大。PRLFM_BSFH 比FHBFSK 约有12 dB 的性能增益,比BSFH 约有5 dB 的性能增益。
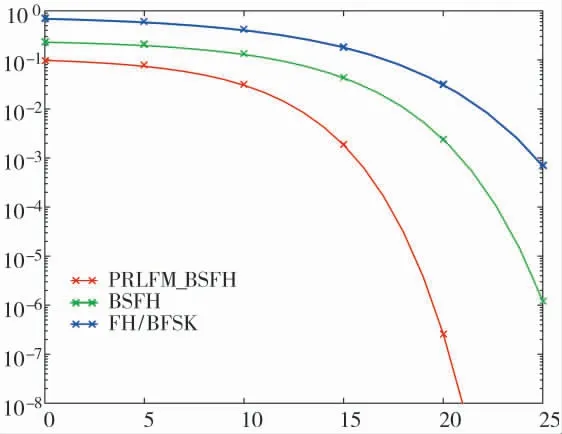
图7 PRLFM_BSFH、BSFH、FH/BFSK在最坏跟踪干扰下的性能
综合以上分析,在窄带跟踪干扰下,存在数据信道和对偶信道同时被干扰的可能,PRLFM_BSFH在不同跟踪干扰参数下都获得了比BSFH 更好的抗干扰效果,说明用LFM 信号作为特征信息提高了接收端检出概率。
图8 对比了3 种通信系统在不同部分频带干扰带宽比例下的通信性能。对于PRLFM_BSFH,干扰带宽越大,干扰到对偶信道时所分配的干扰功率越小,检出概率越高。对于不同的干扰功率应当选择不同的干扰带宽比例。对于BSFH,信干比较小时,最坏跟踪干扰为宽带干扰,而信干比较大时为窄带干扰。当=1,即为宽带干扰时,BSFH 与FH/BFSK 的误码率曲线重合。总体来看,在达到相同误码率的情况下所需的信干比,PRLFM_BSFH 比BSFH 低约4 dB,比FHBFSK 低约5 dB。
4 结论
BSFH 具有较好的综合抗干扰能力,但是其存在一个致命缺点,就是对偶信道被干扰可能会导致通信中断。因此,针对BSFH 的缺点,提出了PRLFM_BSFH 通信系统,该系统在每一跳信号中混频LFM 信号作为特征信息,以此提高对偶信道被干扰时的抗干扰能力。首先构建系统模型,然后对其在不同干扰下的误码率进行推导。通过仿真验证,在不同干扰参数设置下,PRLFM_BSFH 比BSFH 具有更好的通信效果。
