基于动态调节时间的导弹编队逆最优控制算法*
2020-08-22胡朝晖
胡朝晖,黄 伟
(1.西京学院机械工程学院,西安 710123;2.空军工程大学航空工程学院,西安 710038)
0 引言
随着现代反导技术不断升级,导弹突防难度日益增大,类似CIWS(Close-In Weapon System)的导弹防御系统以其全方位、多层次情报搜集能力、战场拦截能力和主动干扰能力,致使单枚导弹在作战中面临巨大威胁。导弹编队控制技术的出现,使得传统单一导弹作战转变为具备协调合作的导弹群作战,可以提高导弹的突防能力和作战效能[1-3]。
导弹编队作战过程中,根据作战环境和目标特点,在有限时间内生成预定的编队几何构型,是导弹编队控制算法设计的难点。韦常柱[4]等将导弹编队队形控制问题描述为最优控制问题,设计了零点保持和非零点保持的导弹编队队形控制器;宋俊红[5]等针对多导弹协同拦截一个机动目标问题,提出了一种带有攻击角约束的多导弹协同控制算法;Namerikawa[6]等基于无向网络连通拓扑,提出一种适用于无人飞行器编队的队形控制算法;文献[7-8]研究了动态领导者切换或存在多领导者的编队队形控制问题,提出了领导者可变的编队控制算法;林志云[9]等应用图拉普拉斯方法,在相对坐标系中建立了无人飞行器编队控制算法;张磊[10]等基于从弹跟踪领弹的编队控制思想,设计了自适应滑模导弹编队控制器。以上控制算法有效地解决了航空飞行器编队队形控制问题,但算法设计过程中,主要分析系统的渐进稳定性或研究领从弹的跟踪问题,未考虑编队系统的动态性能,尤其是动态调节时间等约束条件,从而影响导弹编队系统作战效能的发挥。
鉴于此,本文将导弹编队控制算法设计过程描述为最优控制问题。首先,根据领弹与从弹的相对运动关系,建立系统状态方程,得到相对运动学参数与所需控制力矢量之间的关系模型;其次,基于逆最优控制理论,以领从弹位置误差和速度误差建立性能指标函数,综合动态调节时间等约束条件,逆向得出最优控制量,从而在三维空间中建立导弹编队逆最优控制算法。
1 领弹与从弹相对运动关系建模
在三维空间,以地面某点为坐标原点,建立北-东-天地理坐标系(OXYZ)D,导弹编队中,领弹与第i 枚从弹的相对位置关系如图1 所示。
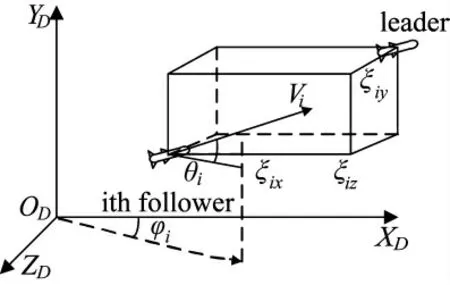
图1 领从弹相对位置关系示意图


式(1)即为单枚导弹的运动学方程,其中,TD,DD表示由弹道坐标系至地理坐标系的转换矩阵。由此可得领弹与从弹i 在地理坐标系下相对运动关系的数学模型为

2 导弹编队逆最优控制算法
导弹编队逆最优控制算法的设计目标是:在领弹与从弹相对运动关系数学模型的基础上,选取适当运动学参数作为控制量,得到在某种性能指标函数下的最优控制量,并使闭环系统的动态调节时间满足设计指标要求。需要指出,在控制算法设计过程中,控制量通常选取从弹控制力矢量Fi,由式(3)可知,转换矩阵TD,DD和矢量fi中包含大量非线性时变参数,若根据式(3)建立系统状态方程,需要进一步采用小扰动或微分几何线性化处理,不能保证系统的能控性。为简化设计,将从弹加速度矢量al作为控制量,由此可得导弹编队系统方程为:



3 仿真实例
导弹编队由一枚领弹和两枚从弹组成,仿真参数如下:从弹1 初始位置坐标(0 m,0 m,10 000 m),初始速度(400 m/s,1 200 m/s,0 m/s);从弹2 初始位置坐标(2 000 m,10 000 m,5 000 m),初始速度(500 m/s,600 m/s,0 m/s);领弹初始位置坐标(10 000 m,10 000 m,10 000 m),初始速度(600 m/s,600 m/s,200 m/s);领弹与从弹1 理想距离(-500 m,-1 000 m,1 000 m),领弹与从弹2 理想距离(500 m,1 000 m,1 000 m);领从弹各轴向理想相对速度0 m/s,闭环系统调节时间90 s,从弹各轴向最大加速度120 m/s2;领从弹初始状态各轴向最大距离误差40 000 m,领从弹初始状态各轴向最大相对速度误差2 000 m/s;假设目标位置坐标为(40 000 m,40 000 m,0 m)。

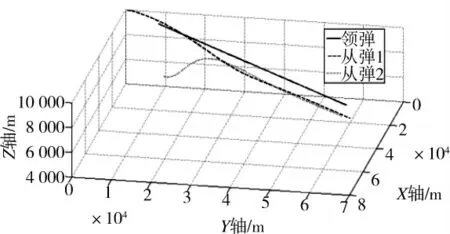
图2 最优编队三维轨迹
图3 和图4 给出了在导弹编队队形生成过程中,领弹与从弹1 相对运动参数的变化情况。由图可知,随着制导时间的不断增加,领弹与从弹1 的距离由初始条件逐步趋近于期望距离,其相对运动速度趋于零,实现了导弹编队队形的生成和保持,从弹1 闭环制导控制系统的动态调节时间满足总体设计要求。
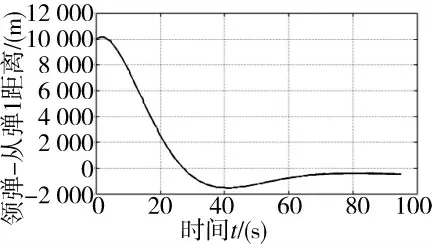
图3 领弹与从弹1 在X 轴距离变化示意
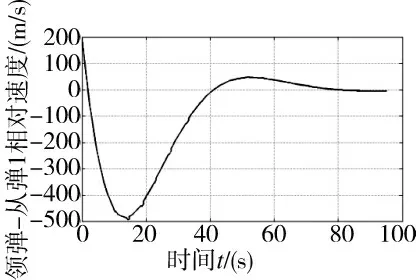
图4 领弹与从弹1 在X 轴相对速度变化示意
图5 和图6 给出了领弹与从弹2 的相对运动参数随制导时间的变化规律,其相对距离和相对速度的变化情况与从弹1 的变化规律一致,随制导时间均趋于理想值。综合上述仿真结果可知,应用本文提出的编队控制算法,导弹编队在动态时间约束条件下,实现了预期队形的生成,并速度保持一致。
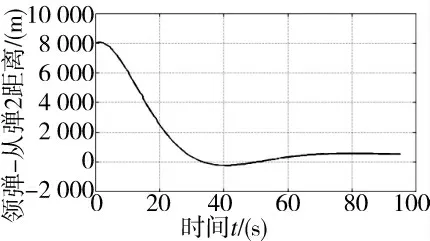
图5 领弹与从弹2 在X 轴距离变化示意
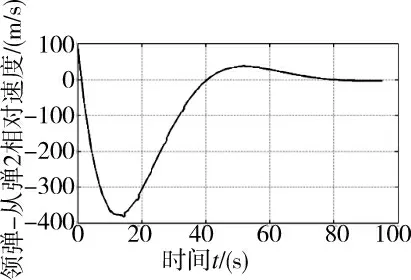
图6 领弹与从弹2 在X 轴相对速度变化示意
4 结论
本文提出的控制算法有效解决了领从结构导弹编队在既定时间内生成理想队形的控制问题,研究总结如下:1)建立了领弹结构导弹编队相对运动关系的数学模型;2)基于逆最优控制理论,兼顾控制量的最优性和闭环系统的动态特性,实现了在系统动态调节时间约束下编队队形的控制,且该算法具有较快的收敛速度和较好的控制经济性;3)控制量算法式结构简单,满足弹载计算的实时性要求,具有较强的工程应用价值。
