动态模糊Petri 网下的Ad hoc 风险评估*

陈赵懿，高秀峰，王 帅，韩月明

（陆军工程大学石家庄校区模拟训练中心，石家庄 050003）

0 引言

Ad hoc 网络具有节点资源有限、不依赖固定基础设施等特点，比传统网络更容易遭受各种安全威胁，如窃听、重放、篡改报文和拒绝服务等等［1］。Ad hoc 网络安全一直是研究重点，但目前对其安全风险的量化评估研究较少，且缺乏成熟的、适用性强的评估框架与模型。张勇等学者［2-5］从Ad hoc 网络可生存性、可靠性、安全路由协议、攻防策略等方面进行了大量研究，但没有对网络风险进行量化。李振富等学者［6-8］结合Ad hoc 网络应用，从战术通信网的抗毁性、通信能力和效能等方面进行了分析研究，提出的评估模型多是基于层次分析法，这些指标体系不能随应用场景的变化而自动调整。例如Ad hoc 网络遭受黑洞攻击［9］，其网络丢包率上升，但网络平均端到端时延等参数没有明显变化，如果指标权重保持不变，那么丢包率对评估结果的影响就无法充分体现。

针对这个问题，本文提出了基于动态模糊Petri网的评估模型，它具有Petri 网的图形描述、模糊系统的模糊推理和评估指标体系结构动态调整的能力。胡涛等学者［10-12］应用模糊Petri 网对地铁、空管、航天等系统进行安全评估。在此基础上，本文模型同时引入动态的变迁阈值和变迁支持度，以模糊规则的前提因子自身状态为基础，以变迁阈值为条件，屏蔽可信度小于变迁阈值的指标，达到对指标权重和指标体系结构进行动态调整的目的，从而适应不同应用场景的风险评估，提高评估准确性、灵敏度和适应性。

本文评估过程分3 步：1）分析Ad hoc 网络安全风险因素，构建动态模糊Petri 网评估模型，这是评估结果好坏的前提；2）获取指标数据，计算Petri网模型的初始状态矩阵和初始权重矩阵；3）执行模糊规则推理，计算网络整体安全风险值，分析评估结果，完善评估模型。

1 动态模糊Petri 网评估模型

1.1 相关定义

定义1 动态模糊Petri 网（DFPN）评估模型为一个十元组

定义2 基本模糊推理规则

IF d1THEN dtarget，用DFPN 表示如图1 所示。定义4 风险等级评价矩阵Q

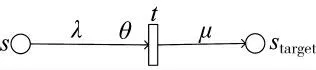
图1 模糊推理规则

参考国家《计算机信息系统安全保护等级划分准则》，本文评估模型设5 个风险等级，如表1 所示，设等级矩阵Q=［0.9，0.7，0.5，0.3，0.1］。

表1 风险等级

1.2 模型构建

Ad hoc 网络安全评价指标的选取和建立是进行综合评价的前提和基础［13］。Ad hoc 网络的安全风险由很多影响因素组成，这些因素在一定程度上相互关联和制约。有学者从资产、威胁和脆弱性等方面分析，也有学者从系统、网络和服务等方面评估［14-15］。参考国内外学者研究的网络攻击与端到端延时、往返延迟、节点转发平均时间、丢包率、吞吐量等指标［16］的关系，依据信息系统安全属性，本文主要从网络可用性、可靠性、信息机密性和完整性角度评估Ad hoc 网络安全，以评估指标为库所，构成DFPN 评估模型，如图2 所示。

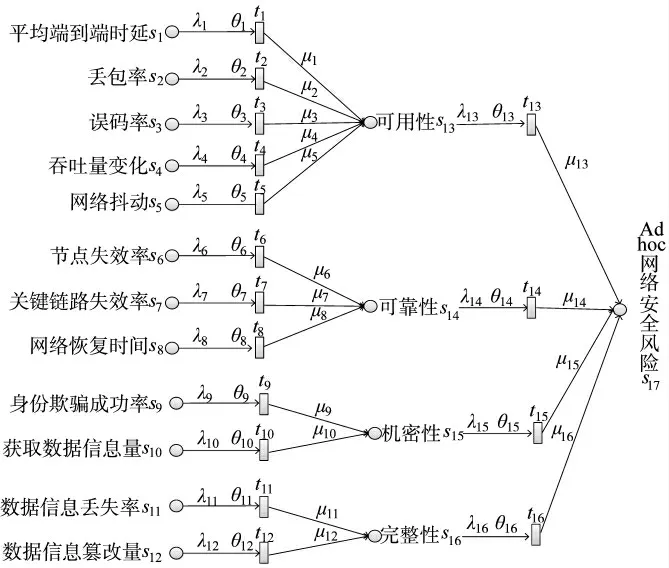
图2 DFPN 评估模型

DFPN 评估模型的变迁对应推理规则，变迁的输入、输出库所分别表示规则的前提因子和结论命题。每个库所对应一个指标，通过指标状态矩阵可计算输入库所对变迁的可信度。根据网络特点与网络运行的历史数据，可对变迁阈值进行设置，提高某变迁阈值，相当于屏蔽了该指标微小变化对整体评估的影响；反之，降低重要指标的变迁阈值，可突出其细微变化对整体评估的影响。根据变迁的阈值与输入库所可信度，可计算变迁对输出库所的动态支持度，本文也表示指标的动态权重。最后，通过模糊规则的推理，更新模型的状态矩阵。

1.3 初始权重矩阵

评估模型中，不同指标权重会导致不同评估结果。本文评估模型引入指标初始权重与可信度，作为输入库所对变迁的初始权重矩阵W 和可信度矩阵。利用模糊层次分析赋权法［17］，对指标权重进行初始化。模糊判断矩阵及性质：

1.4 初始状态矩阵

由于评估模型中指标具有不同量纲和数量级，评估前需对其数据进行标准化处理。对于定性指标和一些无标准数据参考的指标，可结合专家经验与历史数据，用模糊法进行量化。本文利用三角形隶属度函数作为度量依据，对指标数据进行模糊量化。三角形隶属度函数中，数据x 隶属于等级i 的概率为：

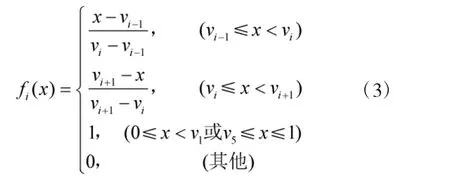
其中，vi可为等级i 区域内某值，一般为中间值。以网络丢包率指标为例，划分5 个等级，从低至高依次 为［0，0.2）、［0.2，0.4）、［0.4，0.6）、［0.6，0.8）、［0.8，1］，那么v1～v5可选（0.1，0.3，0.5，0.7，0.9）。网络丢包率为0.45 时，根据式（3），其隶属度矩阵为［0，0，0.75，0.25，0］。

2 模糊推理算法

模糊推理算法是DFPN 进行推理计算的方法，其算法的优劣直接影响模型的性能和计算速度。由DFPN 的定义和结构求出输入矩阵IN 和输出矩阵OUT；通过模糊层次分析法计算可确定初始权重矩阵W；获取指标数据，经过隶属度函数运算，可以得到初始状态矩阵M（0）；根据网络运行历史数据和专家知识，确定变迁阈值矩阵θ；变迁支持度μ 在模糊推理过程中动态计算。

输入：Step1：Step2：Step3：Step4：Step5：模糊推理算法输入矩阵IN，输出矩阵OUT，评价矩阵Q，初始状态矩阵M（0），变迁阈值矩阵θ，库所初始权重向量新建m×1 矩阵Temp，令k=0（k 为推理计算次数）进行DFPN 推理计算，进入循环计算可信度矩阵images/BZ_31_1663_2605_1860_2649.png比较库所可信度与变迁阈值关系images/BZ_31_1923_2695_2110_2734.png计算规则中变迁对输出库所的动态支持度矩阵μ，某规则中变迁tj 的输出库所为tj·，那么μj 的公式：images/BZ_31_1579_2900_2022_3043.png（4）m 是以tj·为输出库所的所有变迁数量，对于某一输出库所tj·，其所有变迁的支持度之和仍为1，即images/BZ_31_1403_3183_1734_3266.png

Step6：计算变迁发生后的下一状态矩阵，计算公式：images/BZ_32_431_400_1050_444.pngStep7：Step8：输出：（5）如果，转入Step2计算各评估指标的最终评估值images/BZ_32_431_478_765_519.pngimages/BZ_32_840_563_1054_607.png网络风险评估值

DFPN 的推理算法，关键是求解规则中变迁对输出库所的动态支持度矩阵μ 与变迁发生后的下一状态矩阵M（k+1）。μ 为|T|×1 阶矩阵，M（k+1）为|S|×|Q|阶矩阵，M（k+1）的计算复杂度为O（|S|×|T|×|Q|），矩阵运算可并行执行，模糊推理共进行k 次，即M（k+1）=M（k），故算法复杂度为O（|S|×|T|×|Q|）。

3 实验与分析

3.1 实验数据

为验证所提评估模型的合理性和模糊推理算法的可行性，本文利用OMnet++软件进行Ad hoc网络节点故障的简单仿真实验。仿真场景参数设置如表2 所示，共设置20 个节点，8 个节点两两相互通信，其余节点转发。

表2 实验参数设置

随机选取不同数目的网络节点发生故障进行实验，每个不同故障节点数目的实验重复5 次，每次实验持续60 s，取实验数据平均值作为指标数据。故障节点的数目和位置不同，对网络造成的影响也不同。网络节点发生故障后，会导致部分节点孤立、链路失效和部分通信中断，但其他通信可通过AODV 协议重新选择其他链路进行。故障节点突增后，因大量路由需重新选择，会导致网络抖动厉害，故障节点过多会使整个网络瘫痪。实验部分数据如表3 所示，表中仅列出受影响的指标数据。

表3 实验指标数据

3.2 数据分析

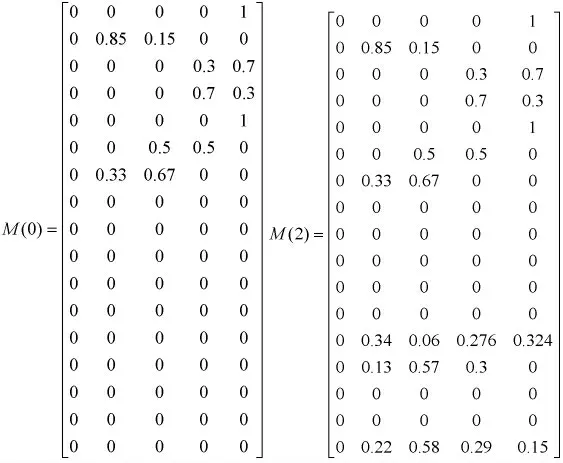
结合实验环境和专家经验，根据模糊判断矩阵，求得各指标初始权重，W=［0.2 0.25 0.225 0.155 0.15 0.33 0.5 0.17 0.65 0.35 0.65 0.35 0.27 0.33 0.18 0.22］。根据网络特点设定变迁阈值，为方便计算统一设定为0.1。以4 个故障节点的实验数据为例进行计算，根据式（3），对指标数据模糊量化，得到初始状态矩阵M（0），根据模糊推理算法，进行第一轮推理，指标对变迁的可信度=［0.1 0.6 0.16 0.24 0.1 0.4 0.57 0 0 0 0 0 0 0 0 0］，此时只有s2、s3、s4、s6、s7的可信度大于各自变迁阈值，其他指标由于可信度小于阈值而被屏蔽。计算变迁对输出库所的动态支持度为μ=［0 0.4 0.36 0.24 0 0.6 0.4 0 0 0 0 0 0 0 0 0］，第1 轮变迁发生后，得到状态矩阵为M（1）；继续推理运算，得到状态矩阵M（2）=M（3），此时推理结束。根据M（k）QT计算，该Ad hoc 网络整体风险值为0.546，风险程度为“中级”。

3.3 与其他模型比较

将本文评估模型与常用的模糊综合分析法［12，16］进行比较，采用同一实验数据与初始权重矩阵，进行模糊综合分析法评估，得到网络整体风险隶属度矩阵F=［0 0.111 8 0.175 1 0.102 0.149 6］，网络整体风险值为0.211 4，风险等级为“较低”，相比于本文模型，其风险评估值低很多。在模糊综合分析法运算过程中，有些指标数据虽然为0，但仍占有一定权重，此时相当于减弱了其他因素的权重，导致无法充分体现其他重要因素对整体风险评估的影响，准确性不如本文提出的评估模型。同样的计算，对比故障节点数为2 和4 时的网络风险，本文模型评估的风险值变化比模糊综合分析法评估的风险值变化要大，灵敏度更高。

4 结论

通过引入动态变迁阈值和动态变迁支持度，本文构建的Ad hoc 网络评估模型，提高了评估的准确度、灵敏度和适应性。

1）动态调整指标体系结构，适应性更强。

安全风险评估指标体系是一个基本框架，需要自动调整结构，以适应不同情况的风险评估。有些网络攻击只影响部分指标数据，但危害很大，如黑洞攻击造成网络大量丢包，但对误码率、平均端到端时延影响很小，此时应剔除不受影响的指标，使指标体系更有针对性。本文评估模型设定了变迁阈值矩阵θ，当某些指标数据变化很小甚至不受影响时，对应的变迁不会触发，屏蔽了该指标对最终评估的影响，达到了自动灵活调整指标体系结构的目的，增强了模型的适应能力和针对性。

2）动态调整变迁支持度，评估更合理。