借助点子图 架起连接算理和算法的桥梁

摘 要：由于算理对于学生来说，比较抽象，且难以理解，这就加大了算理教学工作中的难度。如何将算理的讲解更加具体化，通过形象化的方式使学生进行直观的感受，是当前教学中的重点。通过直观的模型教学，将算理知识进行有效传授，能够帮助学生加深对其理解与运用，这是教学过程中必须落实的内容。

关键词：模型;理解;算理

目前，小学阶段的教学还是以基础为主，而计算就是小学数学的核心。不同于其他学科的直观感受，算理教学相对来说是比较抽象。不恰当的教学方式，将直接影响着教学的效果。当前的教学中亟需分析教学现状，运用科学合理的教学方法，保障教学内容的落实。

一、 学生常常“讲法”不“讲理”

小学阶段的计算教学，需要的是学生对计算的方法和其中的逻辑关系进行理解，而不是简单记住算法。但在课堂教学过程中，经常会使算理教学变得抽象化、边缘化。

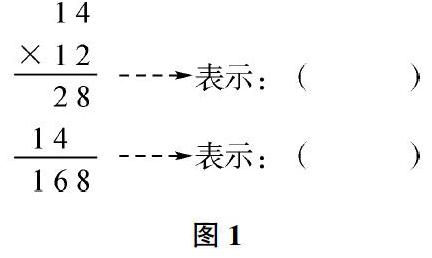
我们在教学质量检测过程时，时常会出现类似下面的题目（图1）：

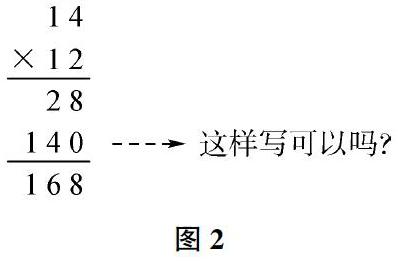
笔者随机对其中的53名学生的情况进行了统计，结果如下：其中计算正确的学生有35名。通过对学生的深入了解，大部分学生都能准确掌握计算的方法，包括数位对齐、用谁乘就和谁对齐等。如果让其分析原因，则大部分学生处于模糊状态或根本不理解，或换个方式提问写成图2的形式，很多学生就不能判断出其正确与否了，在错误的同学中有两名学生对数位对齐还没有掌握。

这样写可以吗？

二、 教学可以“一图抵百语”

在区里的一次备课会上，安排了一节“两位数乘两位数”的计算课。“如何通过合适的方式促进学生对算理的理解，让学生既理解算理又掌握算法？”这引起了笔者和许多与会教师的思索与关注。

一位教师创设了一个“学校举行体操比赛”的情境，然后出示方阵图（图3），让学生了解信息，提问交流后解决“一共多少人？”的问题。在解决上述问题的过程中，学生展示出不同的想法，以下是部分学生的结果：

面对新的问题，学生①至③（图4至图6）都是借助点子图，通过相应的转换方法，把并不熟练的算式改写成熟悉的乘法算式。同样也有学生进行了转换，学生④（图7），通过自己的想法，运用了乘法分配律将12拆分成了10和2，学生⑤（图8）写出了正确的乘法竖式。

三、 应用直观模型的策略

（一）适时呈现，解释疑惑

如笔者在教学三年级“口算乘法”一课时也是让直观模型“姗姗来迟”的：先创设“小明和同学3人去游乐园玩”的情境，接着让学生提出并解决玩不同项目需要多少钱的问题。学生列出算式后，让学生尝试计算20×3，学生想出了“吃0还0”的计算方法，并用加法验证是可靠的。就在学生洋洋得意的时候，笔者抛出问题：“你们能说说这样计算的道理是什么吗。”在学生想用语言表达又表达不清楚之后，老师出示了小棒图、计数器，“看看老师带来的图能不能帮助表达你们的意思。”课件演示捆绑过程（图9）并在计数器上表示（图10）。

学生联系小棒图和计数器理解了“吃0还0”法计算背后所蕴藏的算理。

（二）变化对比，突显结构

我们向学生呈现直观模型时，及时进行变式对比，能加深算理理解，促进学生建构清晰的知识体系。如有位老师在教学“乘法分配律”一课时，为了帮助学生突破难点，理解规律的特定模型，是这样进行教学的：

师：（将图11展示给学生看）根据图中信息求总块数，谁可以列出综合算式？

生：可以用算式（3+4）×5，也可以用算式3×5+4×5。

师：谁能告诉我在这两种算式中，分别是先求的什么，后求的什么呢？

生：算式（3+4）×5，是先求的所有方塊一共7行，后求出总块数。（用图13进行讲解）

生：算式3×5+4×5，是将白色和灰色的方块单独求出，后求出他们的和。（用图12进行讲解）

师：你们认为这两种算法哪个正确，请说明理由。

生：都正确，它们都能算出最后的总数。

师：虽然这两种算式有着一定的区别，但都是表示7个5块的意思，因此我们可以通过等号将它们连接，形成等式。

（三）组合应用，多元理解

当学生面对一个问题，主动联系生活背景思考问题，也是一条直观的途径。清华大学附属小学的张红老师在教学“小数除以小数”时，向学生“打包”提供了生活原型和直观模型：

以图14的5.1÷0.3为例，为了带入学生思考，引导学生理解，教师可以通过多种形式的题型进行全方位理解：

题型一：现有一根绳子，全长5.1米，需要将其分为0.3米的小段绳子，一共能分几段？

题型二：每块橡皮0.3元，明明手上有5.1元，可以买几个这样的橡皮？

题型三：在5.1里面有几个0.3，请圈出来。（图15）

在老师的引导下，学生借助生活原型为例进行了说明商应该为17。而后，学生依靠在直观模型上圈一圈（图16），对算理进行了解释：首先将5.1进行分析，判断其有51个0.1，然后分析0.3，得出有3个0.1。如果想要计算出5.1中0.3的个数，那么就是要求51中有几个3，最后得出17.显然，这些“打包”材料为解题有困难的学生提供了思考背景，为完成的同学提供了反思背景。学生自然借助生活原型解决了怎么算的问题，依靠直观模型解释了为什么这样算的问题。

“一图抵百语”，直观模型抓住了“形”与“理”之间的联系，以“形”的方式，将“理”进行有效的展示出来。通过直观的教学，帮助学生清楚方法的同时，对算理进行掌握。

参考文献：

[1]张红.让知识成为学生的真正营养：“除数是小数的除法”教学与思考[J].小学教学：数学版，2007（9）：20-22.

[2]沈惠芬.对计算教学的再认识：解读特级教师丁杭缨“笔算乘法”一课[J].小学教学：数学版，2008（3）：20-21.

[3]刘加霞.作为“模型”的乘法：对数学概念多元表征的思考[J].小学教学：数学版，2008（10）：46-48.

[4]侯正海.在理解算理的基础上构建算法[J].小学数学教师，2010（7，8）：134-143.

作者简介：苏微丹，福建省三明市，三明市实验小学。