转向机动条件下利用拖船航迹的拖线阵阵形估计

奚 畅，蔡志明，袁 骏

(海军工程大学 电子工程学院， 湖北 武汉 430033)

定常直航是拖线阵声呐的常规工况，但在实际探测过程中拖船常需要进行必要的战术机动，这势必造成拖线阵阵形畸变，从而偏离假设的直线形态[1-2]。大多数波束形成算法都是以精确已知阵形为前提，高分辨空间谱估计算法对阵形误差尤其敏感[3]，实际阵形与理论假设之间的失配不可避免地导致信号处理增益的下降和方位估计性能的恶化。因此，有效地估计阵形对于提高转向机动条件下拖线阵探测性能具有重要意义。

water-pulley模型[4]是一种简单有效的阵形估计方法[5-6]，模型认为拖船机动较为平缓时拖船的横向位移沿阵无衰减地传递到尾端，阵上每个点都沿着前一个点的运动轨迹运动，只需利用拖船当前及历史时刻的位置拟合航迹即可得到拖线阵阵形。其原理较为简单，运算负担小，易于工程实现。但缺陷同样明显，即适用范围有限，拖船机动较剧烈时模型失效，成为制约其工程应用前景的最显著因素。

利用water-pulley模型估计阵形的过程中，对拖船位置坐标进行平滑是拟合航迹前的必要步骤。Gerstoft等[7]根据经验将平滑窗宽度设置为阵长的1.5倍，在海试中利用water-pulley模型校正阵形，得到较好的阵形估计效果，但此平滑经验缺乏理论支持，无法将其应用于其他物理属性的拖线阵。目前尚无公开发表的文献对航迹平滑方法进行研究。

针对water-pulley模型天然存在的适用范围有限问题以及航迹平滑研究领域的真空状态，本文假设在拖船常规机动情况下，声阵段上各点总是沿同一轨迹运动，提出将拖点航迹平滑为声阵段航迹的方法，实现阵形实时估计。

1 声阵段运动特性分析

Paidoussis[8]在惯性坐标系下分析柔性细长圆柱体微元段的受力平衡情况，建立的流体中零浮力缆的运动方程(Paidoussis方程)为：

(1)

式中：m是单位长度的缆质量；M是单位长度缆等体积的流体质量；dc是缆直径；L是缆长；U是缆轴向水流速度；Ct和Cn分别是缆的切向和法向阻力系数；C′t是缆尾部的形阻系数，当尾部处于自由状态时该系数为零。

拖船做简谐运动且缆达到稳态时，缆上各点均做相同频率、不同振幅的简谐运动。将Paidoussis方程无因次化，再代入拖船位移方程，可得零浮力缆的稳态振荡响应公式[9]：

(2)

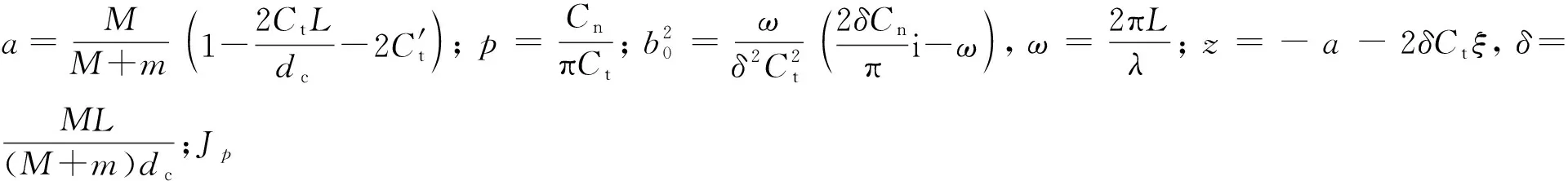
利用式(2)计算不同振荡频率情况下缆上各位置的归一化振幅可知，流体中的缆可看作低通滤波器，无因次频率较大时，拖船处的振荡在向缆尾传导的过程中显著衰减；无因次频率较小时，缆上各位置的振幅与拖船振幅相差较小，可以近似认为缆上各点均沿拖船航迹运动，此即water-pulley模型[4]，又称worm-in-a-hole运动[10]。并且，振幅从拖点到缆尾呈类指数下降，即越靠近缆尾，振幅变化越平缓，缆尾附近振幅不变，下面针对此问题进行分析。

由式(2)整理可得：

(3)

式中前两项与缆上位置无关，令第三项等于g(z)，缆物理属性和振荡频率一定时，振幅|v(z)|可表示为|g(z)|与常数相乘的形式，因此可利用|g(z)|分析振幅随缆上位置的变化情况。由于b0是复数，为讨论方便，不失一般性，假设b0=2reiφ，r和φ可为任意实数，将b0=2reiφ代入g(z)可得：

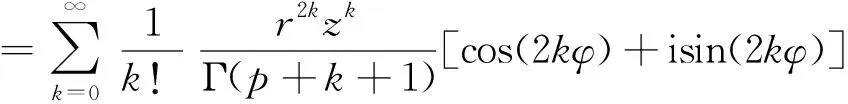
(4)

式中：

对式(4)取模并求导可得：

(5)

(6)

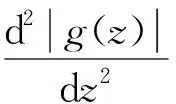
(7)

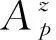
(8)

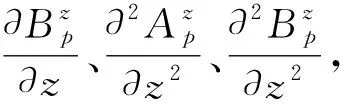
(9)

(10)

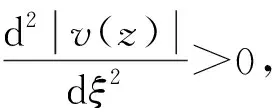
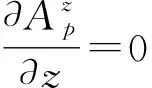
由此得出结论，拖点简谐运动时阵上各点的振幅从拖点到缆尾逐渐减小，且减小速度越来越慢，缆尾附近振幅不变，理论分析结论与计算结果一致。

拖线阵包括拖缆段和声阵段两部分，拖缆段两端分别连接拖船和声阵段头部，声阵段长度通常小于拖缆段。由上述分析可知，拖点简谐运动时，靠近拖线阵尾端的声阵段振幅随缆上位置变化较平缓，即使拖点振幅与尾端振幅相差较大，声阵段上各点振幅依然较为一致。因此，拖点剧烈机动时water-pulley模型失效，但可认为声阵段上各点沿同一轨迹运动，若已知拖缆段尾端航迹，即可得到声阵段运动轨迹。

式(2)可计算零浮力缆上各点的稳态振荡响应，但拖缆段密度大于流体密度且尾端非自由状态，应采用文献[9]方法调整法向阻力系数Cn并代入形阻系数C′t，即可计算得到拖点简谐运动时拖缆段尾端运动特性。

2 声阵段航迹平滑方法

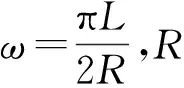
如图1所示，对回转运动情况下拖船航迹进行平滑可以得到航迹的同心圆，平滑结果的半径与平滑窗宽度相关。假设声阵段上各点均沿声阵段头部的航迹运动，且声阵段头部回转半径Ra可通过稳态振荡响应公式计算得到，则可利用合适宽度的平滑窗对拖船航迹进行平滑，得到声阵段运动轨迹。

图1 拖船回转运动时拖线阵示意Fig.1 Array during circular maneuvering

确定平滑窗宽度时，可利用不同宽度的平滑窗分别对半径为R的圆进行平滑，找到平滑结果半径最接近Ra的平滑窗即可。当采用矩形平滑窗时，宽度l可由式(11)近似得到：

(11)

实际侦测过程中，常用的战术机动模式是在直行的基础上调整操舵角度，令拖船以一固定转弯半径进行转向，调整到指定航向后将舵角归零继续直航，完整航迹由圆弧和圆弧两端的切线组成，本文将此称为转向机动，并针对此机动模式进行分析。

考虑转弯角度较大的情况，在拖船转向过程中，拖线阵上各点依次脱离直行稳态并逐渐进入回转稳态；拖船结束转向开始直行后，阵上各点依次脱离回转稳态，拖线阵逐渐被拖直。因此，可将拖船转向机动过程中拖线阵上各点的运动状态变化情况归纳为“直行稳态—过渡态—回转稳态—过渡态—直行稳态”。

用回转运动中得到的声阵段运动轨迹的平滑窗对圆弧运动拖船航迹进行处理，可以得到“直线—弧线—圆弧—弧线—直线”，其中圆弧部分的半径是拖线阵达到回转稳态时声阵段运动半径。

由此可发现，平滑结果的分段线形属性与声阵段分段运动状态属性一致，且平滑结果中的直线和圆弧可以较好描述声阵段在直行和圆周稳态下的特性。虽然平滑得到的各分段长度和衔接点位置与真实情况并非完全吻合，但可以将此平滑结果近似认为是声阵段的运动轨迹，示意图如图2所示。

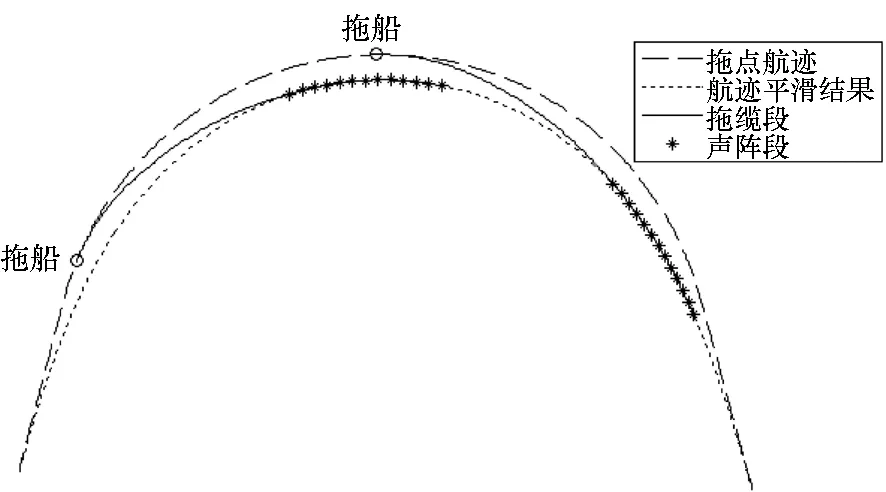
图2 拖船转向机动时拖线阵示意Fig.2 Array during course-change maneuvering

3 阵形实时估计方法

拖船机动过程中需要实时估计拖线阵流形，利用上节所述方法对拖船当前及历史时刻的航迹点进行平滑可以得到声阵段运动轨迹，但无法确定当前声阵段的具体位置。因此需先估计拖缆段的阵形，由拖缆段尾端位置确定声阵段头部位置，进而沿声阵段轨迹确定当前声阵段流形。

如图2所示，如果有一段轴向长度等于拖缆段长度的弧线光滑地连接拖船和声阵段运动轨迹上某点，则可认为这段弧线是拖缆段阵形。连接拖船与声阵段运动轨迹的曲线，可以用完整平滑窗的一部分对距离拖船不足平滑窗宽度的航迹部分进行平滑得到。

为使完整平滑窗和不完整平滑窗的平滑结果衔接部分光滑，应采用三角平滑窗。设窗宽度是W，待平滑航迹的一端为拖船，另一端与拖船沿航迹距离为D，对于所有满足D≤W的航段内坐标点分别进行加权求和，即可得到拖船附近航迹的平滑结果。当D≤(W+1)/2时，平滑窗可表示为：

(12)

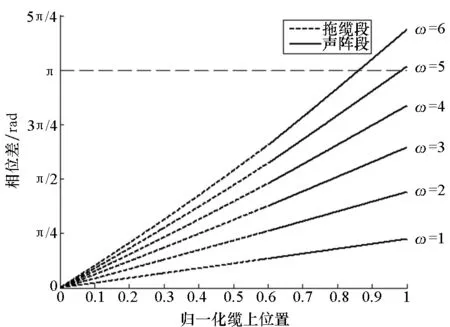
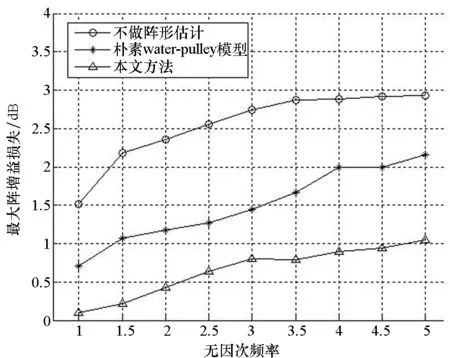
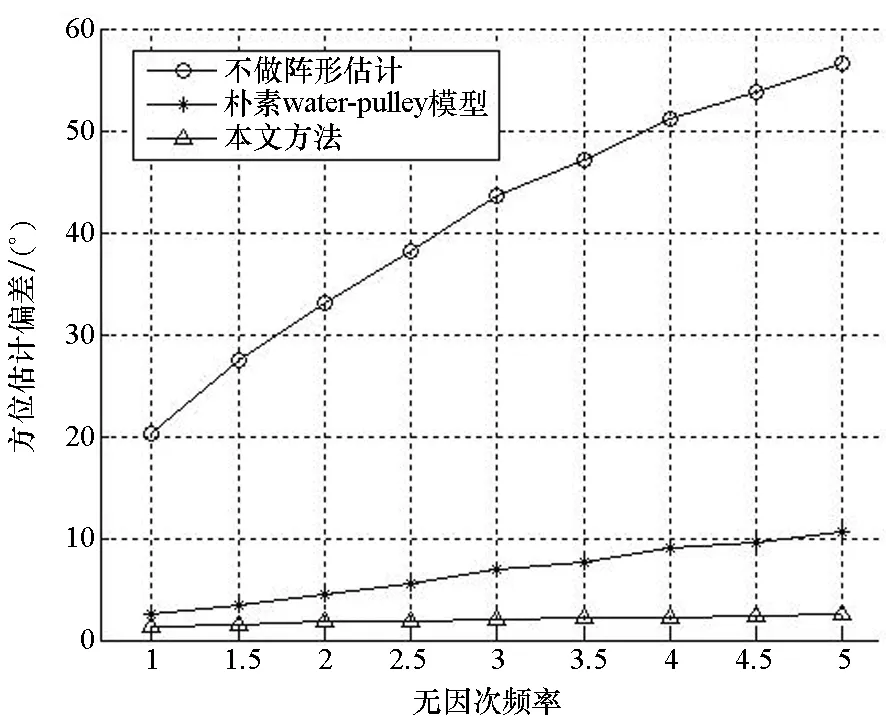
当(W+1)/2

(13)

综上所述，拖船转向机动过程中的阵形估计方法可简述如下：第一步，根据拖船转弯半径及拖线阵物理属性，利用稳态振荡响应公式计算拖缆段尾端振幅；第二步，确定三角窗宽度，利用其对拖船转弯半径对应的圆进行平滑，得到以拖缆段尾端振幅为半径的圆；第三步，利用此三角窗对拖船转向机动轨迹进行平滑，并利用平滑窗的一部分对拖船附近航迹进行平滑，得到拖线阵流形。

讨论两种特殊情况。第一种情况：当拖船转弯角度较小时，拖线阵尚未进入回转稳态就受到拖船直行的影响逐渐拉直进入直行稳态，拖线阵上各点状态变化情况为“直行稳态—过渡态—直行稳态”。在此情况下，拖船航迹的圆弧部分距离较短，若小于平滑窗宽度则无法平滑得到圆弧，平滑结果为“直线—弧线—直线”，阵形估计结果与实际变化趋势相符。

第二种情况：第1节证明越靠近缆尾，振幅变化越平缓，进而认为位于缆尾的声阵段上各点沿同一轨迹运动。然而当拖缆段较短时，声阵段头部可能靠近全阵中部甚至位于全阵前部，此时声阵段头部和尾端振幅存在较大差异，不能认为声阵段上各点沿同一轨迹运动。

阵形估计时，用平滑窗的一部分和完整平滑窗对拖船航迹进行平滑得到拖线阵流形，不同时刻完整平滑窗的平滑结果均在同一轨迹上(图3中点线部分)，而不完整平滑窗并非如此。如图3所示，当拖缆段较长时，估计的声阵段首端位于完整平滑窗的平滑结果上，声阵段上各点沿同一轨迹运动；当拖缆段长度较短时，估计的声阵段首端位于不完整平滑窗的平滑结果上，声阵段首端和尾部并非沿同一轨迹运动。拖缆段长度变化时的阵形估计结果与实际趋势相符。

图3 不同拖缆段长度的声阵段首端示意Fig.3 Top of sonar array for different cable length

4 实验结果与分析

4.1 算法仿真验证

采用表1所示拖线阵参数，假设拖缆段和声阵段均为光滑圆柱体，法向及切向阻力系数分别为1.275 8及0.004 6。利用稳态振荡响应公式计算不同无因次频率缆上各位置的振幅以及相对于拖船的相位差，结果如图4、图5所示。

表1 拖线阵参数

图4 缆上各位置振幅Fig.4 Normalized amplitude of each point on array

图5 缆上各位置与拖船之间的相位差Fig.5 Phase difference between array and tow point

由图4可知，拖点简谐运动时阵上位置越靠近缆尾振幅变化越平缓，即使拖点振幅与尾端振幅相差较大，声阵段上各点振幅依然较为一致，可知第1节的假设合理。

由图5可知，当无因次频率小于5时，缆尾与拖船相位差小于π，满足拖缆坐标系条件，稳态振荡响应模型适用于拖船回转运动的情况。

Ablow模型[11]经过海试数据验证，具有一定的可靠性，可以将其计算结果作为真实值。利用表1所示拖线阵参数，令拖船以不同无因次频率对应的转弯半径转过150°，用Ablow模型计算转向机动过程中的真实阵形，并用本文方法和不对航迹进行平滑的朴素water-pulley模型估计阵形。假设400 m长的声阵段上均匀嵌入81个阵元，将估计阵形、直线阵对应的阵形与真实阵形对比，认为估计阵形与真实阵形各自首尾阵元连线法向之差是阵形估计误差导致的方位估计偏差，分别计算转向机动过程中的平均阵增益损失和平均方位估计偏差，结果如图6、图7所示。

图6 不同无因次频率的阵增益损失Fig.6 Gain loss for different dimensionless frequency

图7 不同无因次频率的方位估计偏差Fig.7 Direction of arrival error for different dimensionless frequency

由图6～7可知，本文方法与朴素water-pulley模型相比可以使转向过程中的平均阵增益提高约0.8 dB，平均方位估计偏差减小约4.7°，与不做阵形估计相比可使阵增益提高约1.9 dB，方位估计偏差减小约39.2°，间接证明了算法的有效性。

进一步分析可知，无因次频率小于4时，本文方法估计阵形依然会造成一定的阵增益损失和方位估计偏差，这是由于本文假设声阵段上各点沿同一轨迹运动，而真实情况是声阵段首尾存在一定振幅差(如图4所示)。无因次频率为5时，转弯半径过小导致真实阵形未进入回转稳态就被重新拖直，本文方法的估计效果未出现明显恶化，依然较为稳健有效，这与第3节的讨论结果一致。

4.2 输入敏感性分析

本文阵形估计方法的关键是确定三角平滑窗宽度，它由拖船转弯半径和拖线阵物理属性共同决定。拖线阵在实际使用的过程中，拖缆段长度可随应用场景变化，其余物理属性均固定不变。因此，算法的输入变量是拖船转弯半径和拖缆段长度，下面分析平滑窗宽度对输入的敏感性。

令转弯半径等于500 m，拖缆段长度从400 m到800 m变化，其余拖线阵参数如表1所示，计算三角窗宽度，结果如图8(a)所示；利用表1所示拖线阵参数，令转弯半径从300 m到700 m变化，计算三角窗宽度，结果如图8(b)所示。

(a) 拖缆段长度变化(a) Length of cable varies

(b) 转弯半径变化(b) Turning radius varies图8 平滑窗宽度变化情况Fig.8 Change of smooth window width

由图8分析可知，三角平滑窗宽度对拖缆段长度敏感，而转弯半径对窗宽度影响较小。拖线阵实际使用过程中，拖缆段长度可以由绞车记录的全阵长度减去声阵段长度得到，而转弯半径很难测量。因此，可以将实际的拖缆段长度和拖船常规操舵角度对应的转弯半径用于三角平滑窗宽度的计算，从而将本文方法简化为一种更易于工程实现的方法。

4.3 海试数据运用

海试数据来源于2018年1月在我国东海海域实施的一次综合性水声试验，试验中拖船航速大约5.5 kn，在60 s时间内发生一次约20°的转向机动，用此船常规舵角对应的转弯半径计算三角平滑窗宽度。不做阵形校正以及用本文方法校正阵形后的方位历程如图9、图10所示。

图9中不做阵形校正的左右舷方位历程图互为镜像，从中选取两个目标进行分析，目标1的舷角从57°变化到73°，目标2的舷角从95°变化到63°。由图10可知，用本文方法进行阵形估计后，目标1在右舷历程图上的轨线以及目标2在左舷历程图上的轨线均变得聚集且清晰，可以判断目标1位于右舷且目标2位于左舷，波束形成效果间接证明了简化算法的有效性和可行性。

需要说明的是，本节在波束形成时采用基于远场平面波假设的波束形成算法，图9中目标3是一个位于近场的目标，因此阵形校正反而造成对于此目标波束形成效果的恶化。

图9 不做阵形估计的方位历程Fig.9 Bearing time record without array shape estimation

图10 用本文方法校正阵形的方位历程Fig.10 Bearing time record using proposed method

5 结论

通过分析缆的稳态振荡响应特性，近似认为声阵段上各点沿同一轨迹运动，设计平滑窗将拖船航迹平滑为声阵段运动轨迹，利用平滑窗的一部分对拖船附近航迹进行平滑得到当前拖缆段阵形，从而实现转向机动过程中阵形的实时估计。仿真结果表明：对于阵元间隔为5 m的81个阵元，所提出的方法与朴素water-pulley模型相比可使转向机动过程中的平均阵增益提高约0.8 dB，平均方位估计偏差减小约4.7°，与不做阵形估计相比可使阵增益提高约1.9 dB，方位估计偏差减小约39.2°，间接证明了算法的有效性。通过输入敏感性分析，对阵形估计方法进行简化使其更易于工程实现，海试数据验证表明简化的方法可行、有效。