BDS在低轨卫星编队高精度相对轨道确定上的应用分析

易 彬，谷德峰，邵 凯，易东云

(1. 国防科技大学 文理学院， 湖南 长沙 410073； 2. 中山大学 物理与天文学院， 广东 珠海 519082)

当前，我国航天事业处于快速发展期，北斗全球卫星导航系统工程、高分辨对地观测系统工程等都在稳步推进，而低轨卫星编队飞行技术以其成本低、功能强大、发射灵活等优点，被广泛应用于各类空间大地测量任务[1]，成为目前国内外航天领域研究的热点问题之一。如分布式干涉合成孔径雷达 (Interferometric Synthetic Aperture Radar, InSAR)卫星系统结合了卫星编队技术与InSAR技术，可实现分布式InSAR地面目标三维定位和合成孔径雷达成像等测量任务[2]，极大地拓展了SAR卫星系统的总体性能。目前，国内外已经研究的低轨卫星编队系统有很多，比如TanDEM-X[3]( TerraSAR-X add-on for digital elevation measurement)、Swarm[4]、重力重建与气候实验[5](Gravity Recovery And Climate Experiment，GRACE)和GRACE-FO[6]( GRACE follow-on)等。

编队卫星系统性能优越，应用前景广阔，但也面临很多关键技术挑战。比如，低轨卫星编队系统对相对轨道的事后确定精度要求极为严苛，以TanDEM-X 任务为例，该任务用于地面高程测量时，数字高程模型产品精度指标满足高分辨率地面信息第三等级精度要求[7]，代表着当今国际 InSAR 系统的最高水平，但前提是相对轨道确定精度达到 1～2 mm(每轴)[8-9]。

目前，各航天大国均将全球导航卫星系统(Global Navigation Satellite System，GNSS)作为相对定轨的主流测量手段[10]，在编队飞行的低轨卫星上安装双频GNSS接收机，通过载波相位差分GNSS(Carrier-phase Differential GNSS，CDGNSS)可以减弱或消除各种公共误差影响，提高观测精度[11]，同时双差整周模糊度具有整数特性[12]，采用双差模糊度固定技术可得到毫米量级的相对轨道[13]。2007年，Jäggi 用批处理最小二乘方法求解GRACE系统的相对轨道，K/Ka波段测距(K/Ka-band Ranging，KBR)检核精度达到0.88 mm[14]。2011年，Montenbruck 利用广义卡尔曼滤波方法求解TanDEM-X的相对轨道，轨道互比对结果表明相对定轨精度可达到每轴1 mm[8]。然而，以上结果都是基于全球定位系统(Global Positioning System，GPS)得出的，无论是从技术独立还是信息安全的角度出发，北斗卫星导航系统(BeiDou satellite navigation System，BDS)都是未来中国低轨卫星编队系统高精度相对轨道确定的首选。

BDS是中国自主研发和建设的导航系统，全星座包含5颗地球静止轨道卫星(Geostationary Earth Orbit satellite，GEO)，3 颗倾斜地球同步轨道卫星(Inclined GeoSynchronous earth Orbit satellite，IGSO)和27 颗中轨卫星(Medium Earth Orbit satellite，MEO)，是目前为止唯一的混合星座[15]。BDS包含三类导航卫星，共35颗，卫星总数多于GPS，可视卫星数增多，观测几何增强，但GEO和IGSO卫星具有区域性[16]。

2014年，Liu等通过仿真实验表明北斗区域导航系统可实现全球范围的相对轨道确定，但轨道精度具有明显的区域差异[17]，且目前BDS的星历误差明显大于GPS，比如GEO卫星的星历误差仍为米量级[18-19]。而北斗全星座建设完成后其确定的相对轨道能够达到什么样的精度，自然成为国内外学者关心的问题。

我国自主研发的低轨卫星编队系统正在部署中，且同时搭载北斗接收机，此时如何利用BDS来实现低轨卫星相对轨道高精度确定已成为关键问题。本文采用仿真实验方法，在文献[19]的基础上，进一步深入研究BDS在低轨编队卫星事后高精度相对轨道确定中的应用，首先分析了编队卫星的可视BDS卫星数，其次讨论了观测噪声对相对定轨精度的影响，然后分析了GEO和IGSO卫星在相对定轨中的贡献，最后研究了BDS星历误差对相对定轨的影响，所得结论对未来BDS应用于相对定轨具有重要的参考价值。

1 编队系统设置和观测数据仿真

表1[20]为北斗导航卫星全星座的轨道参数，利用轨道参数进行轨道积分可获得BDS全星座的星历文件。表2[19]为低轨卫星的轨道参数，同理可获得低轨卫星的轨道文件，其中A和B、A和C组成的两个编队系统，星间距分别为2 km和200 km，钟差均设置为0。根据星历文件，轨道文件和钟差文件仿真可得观测文件，在BDS下对观测文件进行相对轨道求解，利用轨道根数积分所得轨道与利用观测数据求解所得轨道之间的偏差即为轨道精度。仿真时间段为2014年6月9日至23日。

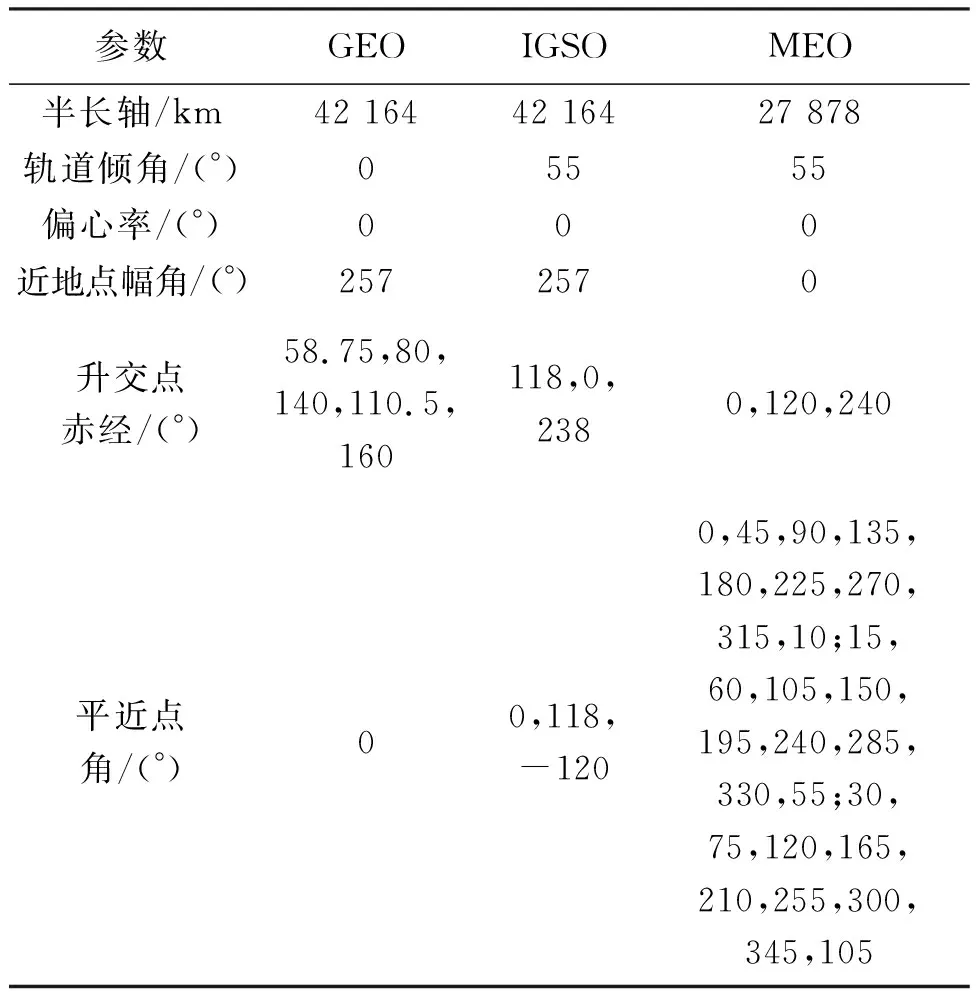
表1 北斗导航卫星的轨道参数[20]

表2 低轨卫星轨道参数[19]

图1为500 km空域平均可视北斗卫星数，最大为18颗，平均约9.7颗，均高于北斗2代区域导航系统[17]，同时由图1可知，BDS的分布具有显著的区域差异，亚太地区可视卫星数明显高于非亚太地区，这主要是由GEO和IGSO所造成的，对此，选择东经55°至东经180°，南纬55°至北纬55°为亚太地区[19]，深入分析BDS在不同区域的相对定轨精度，以及GEO和IGSO对低轨卫星相对轨道确定的影响。

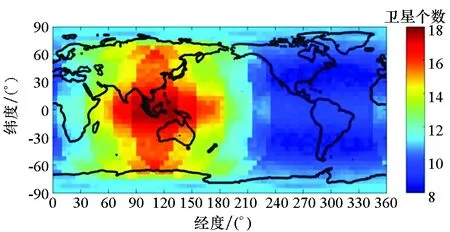
图1 500 km 空域平均可视北斗卫星数Fig.1 Average visible BDS satellites on altitude of 500 km

仿真的观测数据包括双频伪距和载波相位，观测噪声的标准差分别为σP=0.5 m和σL=0.002 m[19]，使用的频率包括B1和B3，采样间隔为10 s，高度截止角为5°。图2统计了15天A和B的共视BDS卫星数，平均可视BDS卫星数约为9.21，且共视卫星数小于等于3的情况约仅占0.19%，相比之前北斗2代区域导航系统[17]，BDS下的共视卫星数明显增加，更有利于全球高精度的相对轨道确定。

图2 低轨卫星A和B的共视北斗卫星数Fig.2 Visible BDS satellites from A and B

2 高精度相对定轨模型

通过构造双差观测方程，可完全消除导航卫星钟差和低轨卫星钟差，有效提高定轨精度[21-22]，双差观测方程可以模型化为式(1)。

(1)

式中，上标j和k代表导航卫星，下标A和B代表低轨卫星，P和L分别为伪码和载波相位观测数据，ρ表示真实的几何距离，f1和f2为所选的两个频率，I为一阶电离层延迟，λ为载波波长，N为模糊度参数，ε为其余误差。需要说明的是，相位缠绕、GNSS发射天线相位中心、相对论效应通过已有模型进行修正，未在公式中列出。

在双差观测方程的基础上构建式(2)所示的双差无电离层组合，消除一阶双差电离层路径延迟的影响，再进行简化动力学批处理最小二乘相对定轨。

(2)

此时，待估参数主要包括：初始轨道参数、模糊度参数、太阳光压系数Cr、大气阻力系数Cd和经验加速度矢量。基于国防科技大学定轨工具包 (National University of Defense Technology orbit determination ToolKit，NUDTTK)软件平台[23]的高精度相对轨道确定的模型选择和参数设置如表3所示。

表3 基于NUDTTK的相对轨道确定策略[19]

NUDTTK是由国防科技大学自主研制的定轨软件平台，文中实验均在NUDTTK上完成，该软件平台已成功应用于GRACE、TanDEM-X等编队卫星的轨道求解， 如2012年，涂佳利用简化动力学方法，求解GRACE编队的相对轨道，K波段测距(K/Ka Band Ranging, KBR)系统校验标准差为1.26 mm[7]；2015年，Ju等改进了机动附近的数值积分方法，GRACE机动条件下实测数据相对定轨结果KBR检核精度为0.7 mm[24]；2017年，Gu等通过优化整周模糊度固定策略和相对相位中心变化估计方法，得到的GRACE相对轨道KBR检核结果为0.68 mm[25]。基于NUDTTK的相对定轨具体流程如图3所示。

图3 基于NUDTTK的相对定轨流程图Fig.3 Flow chart of the NUDTTK based PROD

3 结果分析

3.1 观测噪声的影响

图4 低轨卫星A和B 15天的相对定轨三维方向精度Fig.4 PROD results in 3D of A and B in 15 days

在高精度相对定轨中，钟差、一阶电离层延迟等可通过差分完全消掉， 而星历误差和观测噪声无法通过差分消除，是本研究关心的主要问题。仅考虑伪距和载波相位的观测噪声时，低轨卫星A和B 15天的相对定轨结果如图4所示，平均精度为0.74 mm，这表明在仅受观测噪声影响时，采用BDS的相对定轨精度可达到毫米量级。进一步分析BDS下低轨卫星的全球相对定轨精度，以5°× 5°为区间统计了15天的相对定轨精度，如图5所示，相比北斗2代区域系统[17]，BDS的平均相对定轨精度优于1 mm，且没有明显的区域性，可实现低轨卫星编队相对定轨全球服务。

图5 低轨卫星A和B 相对定轨精度的全球分布Fig.5 Global distribution of PROD results of A and B

3.2 GEO和IGSO卫星的影响

由图1可知，亚太地区的可视卫星数明显居多，表4为亚太地区与非亚太地区15天仅考虑伪距和载波相位观测噪声时相对定轨结果在卫星轨道径向(R)、飞行方向(T)、法方向(N)和三维(3D)方向的精度，亚太地区和非亚太地区R、T、N、3D方向的精度分别为0.26 mm、0.48 mm、0.40 mm、0.68 mm和0.27 mm、0.55 mm、0.44 mm、0.76 mm，亚太地区的相对定轨精度略高于非亚太地区。

表4 低轨卫星A和B的相对定轨精度

为了深入分析GEO卫星和IGSO卫星对相对定轨的作用，分别统计了仅MEO卫星和MEO+GEO+IGSO卫星在全球、亚太地区和非亚太地区的相对定轨精度，如图6所示。仅MEO时15天的平均相对定轨精度在全球、亚太地区和非亚太地区分别为0.83 mm、0.82 mm和0.83 mm，而MEO+GEO+IGSO时分别为0.74 mm、0.68 mm和0.76 mm。GEO和IGSO卫星只分布在亚太地区上空，但对全球范围的相对定轨都有提升作用，主要原因可能是相对定轨中双差整周模糊度固定采取分段区间的形式，亚太地区观测数据的增多，可增强整个解算区间的约束[19]，因此可提升全球的相对定轨精度，但对亚太地区的提高要略高于非亚太地区。

(a) 全球(a) Global

(b) 亚太地区(b) Asia-Pacific region

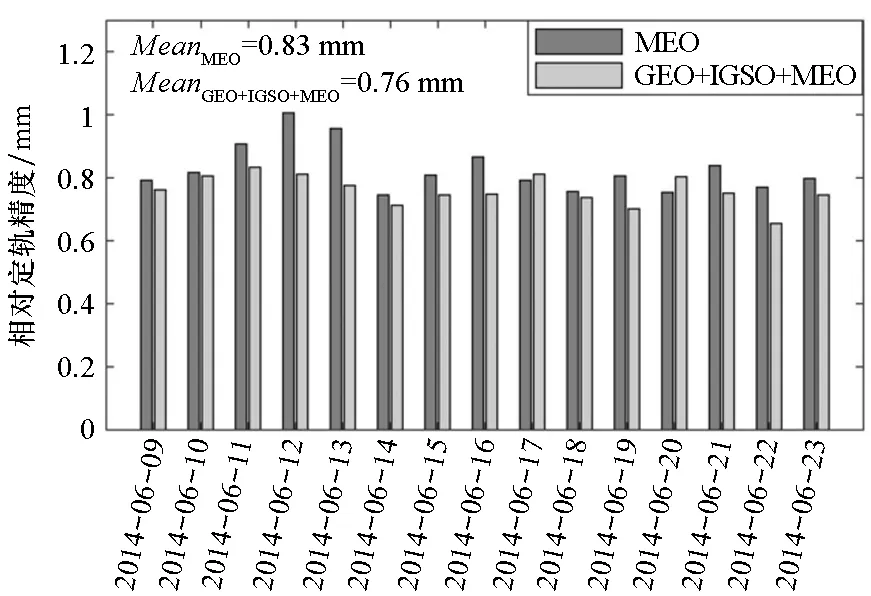
(c) 非亚太地区(c) Out of the Asia-Pacific region图6 在GEO+IGSO+MEO和MEO情况下的低轨卫星A和B的相对定轨精度Fig.6 PROD results of A and B based on GEO+IGSO+MEO and MEO

3.3 星历误差的影响

在高精度相对定轨中，通过CDGNSS可以差分掉大部分的星历误差，但是目前北斗卫星的精密轨道产品精度较差，如GEO卫星的星历误差仍有数米[18]，不容忽视。因此，本文通过仿真实验分析了星历误差对相对定轨的影响，按式(3)在BDS卫星的轨道文件中加入星历误差，

(3)

其中，下标j代表导航卫星，σj为表 5中对应的值，Tj为轨道周期，φj为随机项。图7为2014年6月9日R方向星历误差示意图，GEO、IGSO、MEO卫星各选取2颗，星历误差具有明显周期性规律，且周期与轨道周期基本相同，随机项φj的加入使得星历误差不会被差分，基本符合实际环境。

表5 仿真星历误差大小[18]

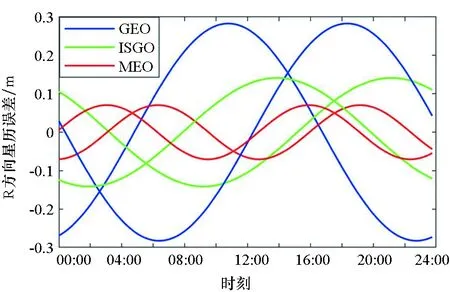
图7 R方向添加的星历误差大小示意图Fig.7 Errors added to ephemeris in R

保持观测噪声和观测数据不变，表6为15天的平均相对定轨精度，可知，在低轨卫星A和B中加入星历误差对相对定轨结果的影响可以忽略。星历误差对单差数据的影响如式(4)[1]所示。

(4)

rAB(t)=rB(t)-rA(t)

(5)

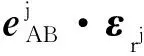
表6 有无星历误差时A和B的相对定轨精度

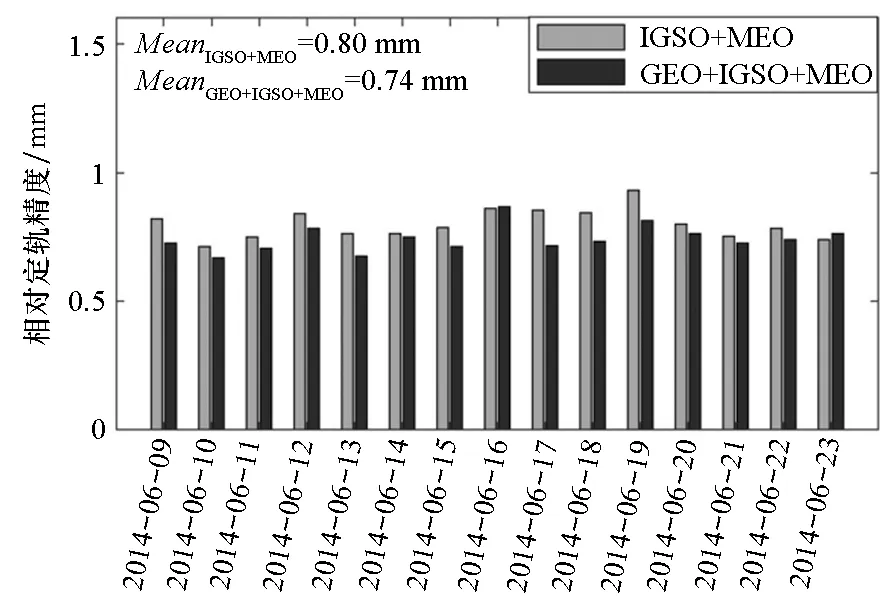
(a) 无星历误差(a) Without ephemeris errors

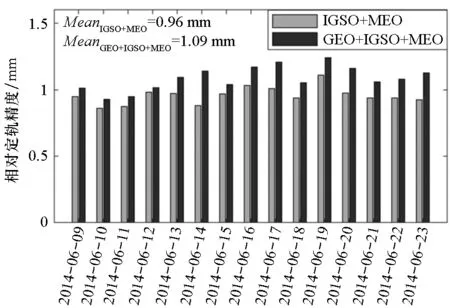
(b) 有星历误差(b) With ephemeris errors图8 低轨卫星A和C在无星历误差和有星历误差下的相对定轨精度Fig.8 PROD results with and without ephemeris errors

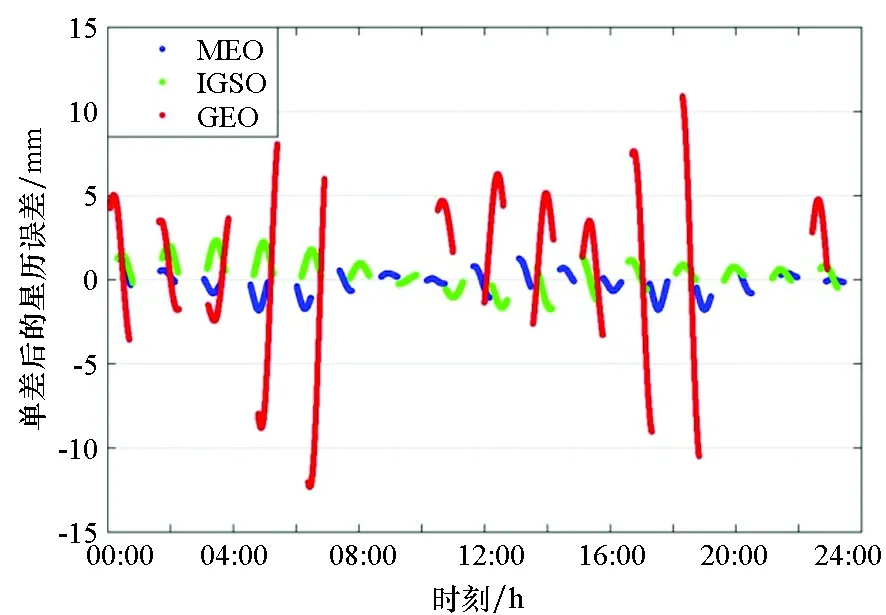
图9 低轨卫星A和C单差后的星历误差Fig.9 The SD ephemeris errors of A and C

综上可知，对于远距离编队卫星相对定轨必须考虑GEO卫星的星历误差，进一步分析星历误差对单差数据的影响，图9为2014年6月23日GEO、IGSO和MEO三类卫星添加星历误差后单差数据的变化。同类卫星的星历误差量级基本相同，因此每类卫星仅列举1颗卫星来说明。MEO和IGSO卫星单差后的星历误差最大约2 mm，平均小于1 mm，GEO卫星单差后的星历误差平均约4 mm，最大可达到厘米量级。但北斗全星座中仅有5颗GEO卫星，并未对整体定轨结果造成厘米量级的影响。未来BDS应用于远距离编队卫星高精度相对定轨时，应对MEO、GEO、IGSO卫星设置不同的权值，以降低星历误差对定轨结果的影响。

4 结论

本文研究了基于BDS的低轨卫星编队相对定轨，对未来BDS应用于低轨卫星编队相对轨道的确定具有重要的参考价值。首先，分析了全球可视BDS卫星数，500 km空域平均可视BDS卫星数约为9.7，由于GEO和IGSO的存在，BDS在亚太地区的可视卫星数明显居多。然后，在仅受观测噪声影响的情况下，BDS求解的相对定轨精度平均约为0.74 mm。亚太地区与非亚太地区15天的平均相对轨道精度分别为0.68 mm和0.76 mm，两个区域的相对定轨精度基本一致。最后，GEO卫星目前的星历误差对近距离编队相对定轨的影响可以忽略，但当星间距离增大到数百公里时，GEO卫星的星历误差对高精度相对定轨的影响不可忽略。