基于开源计算流体力学软件SU2的钝体翼尖涡研究

2020-08-14钱晓辉刘剑明

沈阳航空航天大学学报 2020年3期

崔青,钱晓辉,刘剑明

(1.中国航空工业空气动力研究院，沈阳 110034;2.南京航空航天大学航空学院，南京 210016;3.江苏师范大学数学与统计学院，江苏徐州 221116)

众所周知，升力面后面的流动如机翼，会导致持续且强烈对称的有组织尾涡涡旋结构或翼尖涡旋,而近翼尖涡旋，对于流体力学和空气动力学研究具有重要的应用。因此，人们对翼尖涡旋进行了广泛的实验和数值研究。Devenport与Rife等[1]通过风洞实验使用热线给出了矩形NACA0012翼下游远场方向尾涡。Giuni 与Green[2]使用烟雾可视化技术研究了NACA0012翼方形翼尖与圆形翼尖的近场涡形成，揭示了低雷诺数3000下的近场主涡、次涡的相互作用。除风洞实验外，计算流体力学CFD工具在工程应用中也越来越流行，计算流体力学已经成为除风洞试验外，最经济有效的方法。比如张明华与刘薇等[3-4]开展不同湍流模型翼尖涡模拟研究。最近，Liang与Xue等[5]通过分离涡模拟(DES)方法研究了雷诺数 1.8×105攻角 α=8°、10° 时，矩形NACA0015翼方形翼尖涡，计算得到的翼尖流向涡量与实验结果进行了比较，但因涡量包含剪切或拉伸[6,7]，计算结果并不能客观反映涡旋运动。Lee与Han等[8]针对NACA 0012矩形翼，通过数值方法研究了雷诺平均(RANS)下，当雷诺数Re=1×105攻角 13° 与 30° 时的方形翼尖涡生成，同样使用涡量也混合了剪切与拉伸，增加了分辨次涡与主涡的相互作用的难度。因此，为了进一步研究翼尖涡的形成与相互作用，有必要考察新的涡表示方式。

涡是世界上普遍存在的自然现象。涡旋运动在流体中起关键作用，但如何解决这个问题仍然是有争议的，而缺乏统一的涡旋定义，往往导致涡旋的可视化和理解湍流中的涡旋结构的困惑[6-7，9]。实际上，湍流的显著特征之一是流体充满各种大小和强度的无数旋涡。旋涡的形成与发展和湍流的生成与发展密切相关。但是，缺乏普遍接受的涡旋定义严重阻碍人们深入理解湍流的机理[6-7，9]。最近，Liu C等[9-10]指出涡量不能代表当地流体的刚性旋转，而应该将涡量进一步分解为旋转部分和非旋转部分。基于这一概念Liu C等[4,6-7]给出了一种刚性旋转涡向量Rortex/Liutex，详细讨论也可参见作者及他人近期的论文[11-13]。

本文通过开源计算平台SU2(Stanford University Unstructured)，通过Rortex/Liutex涡定义，研究了矩形NACA0012翼方形翼尖纯刚体涡的生成发展，揭示了次涡与主涡生成与相互作用。

1 SU2计算平台与软件结构

目前CFD的开源软件中，openfoam是最为热门的软件，吸引了大量的科研人员的使用与继续开发，但openfoam比较繁杂，具有一定的学习难度。最近，对于航空航天相关问题，斯坦福大学的开源软件SU2因其程序架构清晰，获得了广泛的关注，引起了很多航空设计课题组的兴趣[14-16]。作为越来越流行的SU2软件，它提供了在非结构网格下求解基于偏微分方程(PDE)问题的软件一般框架，目前其主要的两个功能是CFD和气动优化[8]。SU2软件框架由C++程序及Python脚本集成而成，通过C++类面向对象特征，使用继承、多态等实现软件不同功能及多物理场模块，支持任意变形、运动网格与旋转坐标系，结合外部自适应网格模块实现高效的网格自适应。

SU2的高层次C++类结构中，作为最具代表性的SU2软件的功能模块是SU2_CFD。在SU2_CFD中，最顶层定义了一个驱动程序类 CDriver,如图1所示[14]，它主要控制多物理场模拟的解过程。在此类中，实例化几何、物理以及求解特定问题的数值方法。CDriver类中包括下面类的实例：CConfig、COutput、CIntegration、CIteration，其中最核心的类就是CIntegration和CIteration。在SU2_CFD中使用CIntegration的指针通过多态调用子类CMultiGridIntegration或CSingleGridIntegration来集成特定的控制方程，并开展多重网格加速计算，通过CGeometry、CSolver和CNumerics子类的实例进行时间和空间上的积分，而CIteration 类及其子类完成不同物理模块的单步迭代。在SU2软件中，计算工具的核心功能就是分别嵌入管理几何的CGeometry类，求解器功能的CSolver类和数值方法CNumerics类中。

CGeometry类读入与处理网格，输入的网格结构是一种特有的以SU2为后缀的网格，这种网格已经可以通过商用软件比如Pointwise直接生成。CGeometry类的子类CPhysicalGeometry 建立了SU2软件中格点有限体积方法的对偶网格。CSolver类定义了求解的过程，它的每一个子类用来求解一个特定的控制方程，比如CEulerSolver 类给出求解可压缩无粘性Euler方程的求解器，而CTurbSolver类用于求解湍流模型。CNumerics类使用输入文件中设置的方案参数，通过不同指定方案离散化控制方程组，再经由有几个子类为对流通量、粘性通量以及给定的偏微分方程中可能存在的任何源项提供广泛的离散化技术。

2 数值方法与Rortex/Liutex涡定义

SU2是关于偏微分方程模型的集成解决平台，可以求解各种通过偏微分方程描述的物理工程问题，作为例子，我们仅介绍CFD相关部分。

考虑微分形式的Navier-Stokes方程

(1)

其积分形式是

(2)

对公式(2)，使用对偶网格格点有限体积方法，采用二阶近似可以得到半离散形式

(3)

其中对流通量积分可以使用HLLC、Roe等数值通量，通过使用MUSCL方法得到二阶精度，梯度计算可以采用Green-Gauss方法或者最小二乘法，而粘性项则采用中心格式，时间推进采用Runge-Kutta显格式或者LU-SGS隐格式。为了封闭RANS方程(1)或者(2)的求解，需要求解湍流模型，在SU2中主要提供SA湍流模型与SST湍流模型，作为推荐，一般对于湍流模型的求解，只使用一阶精度迎风格式。如果考虑大分离流动，可以使用脱体涡模拟方法DES/DDES[17]。

因为涡量混合了剪切与拉伸，不能区分层流边界层与旋转。为了显示计算产生的涡结构，需要使用特殊的涡识别方法[9,10]。目前工程中比较流行的涡识别方法是Q标准[18]，表示为速度梯度张量▽V的第2个伽利略不变量

(4)

其中B、A分别是速度梯度张量的反对称张量与对称张量。使用Q标准，在Q>0的区域，认为有旋转，并通过其等值面表示涡的形态，但其不能区分剪切，从而会造成剪切污染，且涡的形态和阈值相关，不同的阈值可能得到完全不同的涡形态，并产生错误的结论[9-10]。涡应该既有大小也有方向，也就是旋转轴，但目前流行的涡表示方法Q标准、λ2与Δ等都是标量，且并没有明确的物理意义[7,9,10]。

最近LiuC等[7,9,11]提出了一种涡向量定义，Rortex/Liutex向量，不但给出了旋转方向，还有刚体旋转大小，并能够区分剪切层与旋转。Rortex/Liutex向量的大小可以用于涡显示，其涡形态不会被剪切污染，而且具有强的涡形态保持能力[13]。根据Rortex/Liutex涡理论，当速度梯度张量有一个实特征值与两个共轭复特征值时，代表瞬时流线呈现圆形或螺旋型，即存在旋涡结构，此与Δ方法和λci方法在判断是否存在涡结构是一致的，但Δ方法和λci方法仅使用到速度梯度张量的不变量和特征值，并没有给出明确的旋转方向的概念，而且用于表示涡的量没有明确的物理意义，且缺乏特征向量方向所提供的信息。当速度梯度张量有3个实特征值时，代表流体微团在3个特征方向只有拉伸或压缩，没有旋转运动，也就是没有涡，此时Rortex/Liutex向量为0；当速度梯度张量有一个实特征值λr和两个共轭的复特征值λcr±iλci时，实特征值对应的特征向量方向只有拉伸或压缩，而涡旋转运动只能发生在垂直于实特征向量r的平面内，此时的实特征向量方向即为当地流体微团的旋转轴，而大小定义为垂直于实特征向量r的平面内两倍的最小角速度。用简单的显公式，可以将Rortex向量表示为[13]

(5)

其中ω表示涡量，r表示实特征值对应单位特征向量方向(取和涡量内积大于0的方向)，λci表示复特征值的虚部。

3 数值实验与分析

3.1 代码验证

为验证SU2软件的有效性，首先考察二维NACA0012攻角与升力系数的关系图[19]。此标准模型问题的流动状态中，雷诺数Re=6×106，马赫数为0.2，计算非结构网格如图2a所示，计算采用二阶Roe格式离散对流项，并使用SA湍流模型封闭RANS方程的计算。图2b给出了升力系数CL与攻角α的计算结果以及实验比较。目前的计算除了在高攻角时因分离流动湍流模型的缘故与实验有偏差外，攻角一直到 15° 升力系数结果都和实验能够很好吻合。此外，升力系数CL与攻角α也较好显示了升力系数CL与攻角α的2π斜率规律。

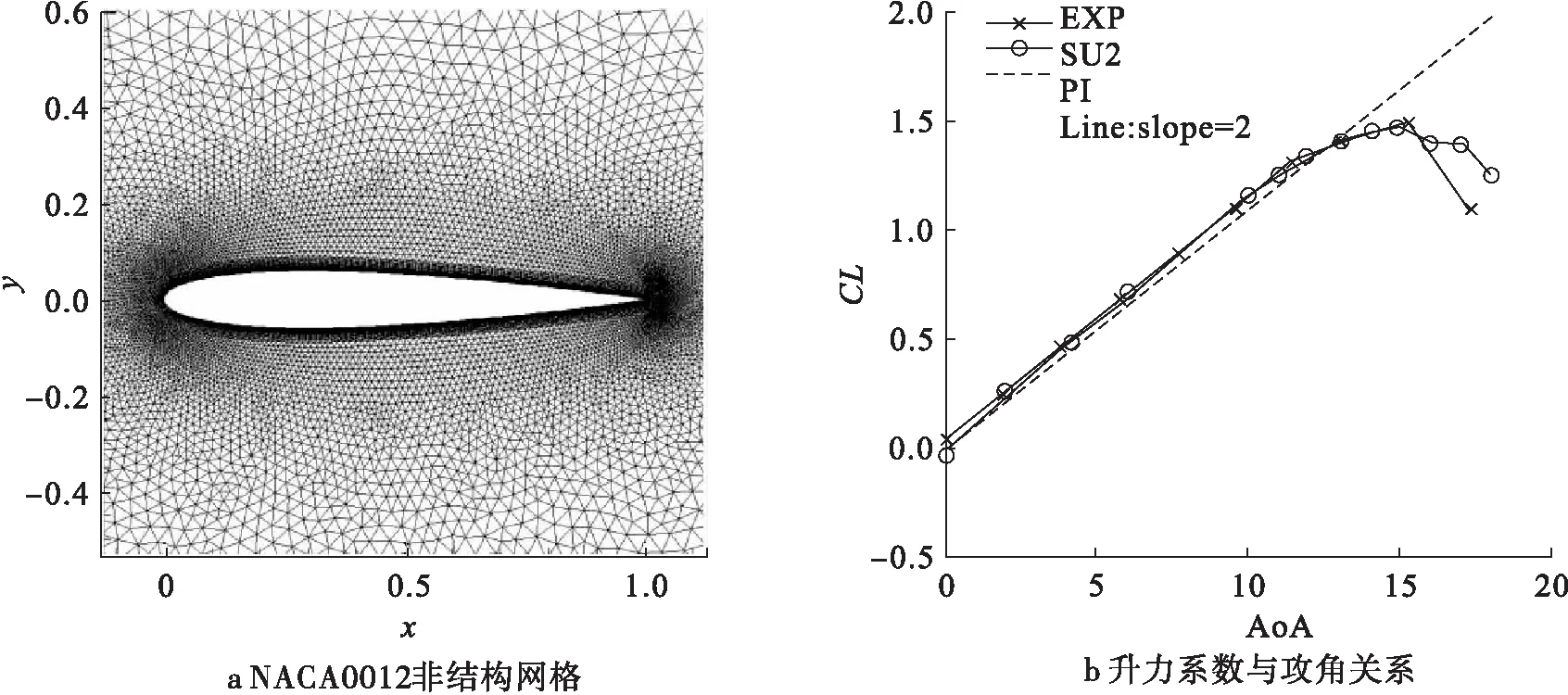
图2 数值验证

3.2 方形翼尖涡识别

对于三维复杂流体，本文考虑三维NACA0012翼型钝体翼尖涡流，雷诺数是Re=2×106，马赫数为0.2，攻角12°，半翼展长为2.5倍弦长。计算采用混合六面体与三棱柱网格，共大约200万个非结构网格，最小网格壁面距离约为2×10-6。图3a为翼端壁面网格，图3b为翼端2.5%弦长截面位置(如图3a所示)的压强系数与实验结果的比较，结果除了因上翼面主旋转涡的存在，压强系数与实验大约在x/c=0.35和x/c=0.75 附近有偏差外，其他位置和实验相符。

图3 NAC0012翼型钝体翼尖网格与压强系数

图4a为使用涡识别Q标准给出的翼端涡等值图，清晰显示涡在翼梢卷起旋转拖出去的长尾涡，且流线围绕涡等值面。图4b为涡向量Rortex大小R的等值面图，此等值面清晰反映了钝体翼尖涡。比较图4两图可以发现，使用Q标准，翼面上很多地方Q>0，而 Rortex量R只在翼尖与前缘显示，这与Q标准会被剪切污染，而Rortex是纯刚体旋转，没有剪切污染的理论相符[7，9]。