谱共轭梯度算法反演航天器在轨瞬态外热流
2020-08-15杨国栋田宇沃张庆新
于 洋,杨国栋,田宇沃,张 航,张庆新
(沈阳航空航天大学 自动化学院,沈阳 110136)
地球轨道运行的航天器在轨运行期间,主要受到来自太阳的直接辐射、太阳自地球的反射和来自地球的红外辐射。卫星的空间外热流对确定卫星的极端工况、热控系统设计、热保护系统影响很大。目前,确定卫星空间外热流的方法主要为工况遍历方式,工作量较大。对卫星空间外热流的计算和分析目前还缺乏行之有效的方法。
因此,为了防止航天器因外部热流的影响导致热控制系统故障,J.X.Wang等[1]提出了一种采用分布式热控制策略的新型主动抽运回路热控制系统。W.F.Wu等[2]提出了可用于航天器的形状稳定的相变材料(PCM),该材料具有高导热性,不需要紧密包装。但他们并没有对航天器外热流进行估计。目前一些研究人员开始对航天器外热流进行计算,刘洋等[3]等基于积分定义法、平行光线法、近似法和插值法提出了太阳系行星际轨道航天器的外热流计算方案。李世俊等[4]为了得到准确的二维变姿态空间相机外热流数据,提出了一种在J2000坐标系下进行二维变姿态空间相机的外热流算法。谢吉慧等[5]为提高外热流模拟的准确性,针对如何确定外热流模拟装置与航天器的结构匹配性这个难题,依托三维扫描技术建立了一套数字化结构匹配方法,解决了多站测量拼接误差累积问题。以上在航天器外表面直接测量热流的方法需要消耗重量、空间和功率等航天资源,加重了航天器运行负担。因此本项目考虑非线性反问题的方法辨识航天器表面外热流。反问题方法是根据可观测量的测量值反演系统中的参数或未知信息。目前,该方法在航空航天领域中的导弹制导[6]、火箭推进系统故障[7]等方面得到了良好的应用。热传导反问题是反问题的一个分支,一般是通过测量温度反演和计算热传导模型边界条件的物性参数。对于热流的反演,B.Ghadimi等[8]和H.Wang等[9]分别使用了人工神经网络方法反演估计热流。H.Wang等[10]为了测量表面传导或对流的热流量分布,提出了一种基于红外(IR)技术和逆热传导的非接触测量方法。M.Cui 等[11-12]对Levenberg- Marquardt 算法进行改进,估计了二维热传导方程的边界热流。Y.Yu 等[13]提出改进的权最小二乘差分进化算法辨识铸坯二维热传导模型的换热系数。A.V.Nenarokomov等[14]基于热传导反问题的方法估算先进材料表面的热流。宋馨等[15]采用共轭梯度算法反演了航天器的外热流。
但是这些研究方法并没有考虑测量误差对反演结果的影响。航天器外热流的反演会产生反问题的不适定性,即测量数据中含有少量的误差就会引起计算结果偏离真实值很远,如何解决反演热流中存在的不适定性,消除测量误差对反演结果的影响,是一个值得从理论和实际中研究的问题。因此,本文建立了热传导反问题的数学模型,提出了基于偏差原则的谱共轭梯度算法,Matlab仿真结果验证了本文方法的有效性。
1 数学模型
本文所研究的航天器外热流为一维瞬态导热问题,一维瞬态导热方程为
(1)
式中:T为温度(K);τ为时间(s);k为热传导系数(W/(m·K));ρ为密度(kg/m3);cp为比热容(J/(kg·K))。
内侧即朝向航天器内部的一侧(x=0)为绝热边界条件:
(2)
外侧即朝向外界空间环境的一侧(x=L) 使用第3类边界条件:
(3)
式中:q为研究对象的吸收外热流值(W·m),包括吸收的太阳辐射、天体的红外辐射以及天体反照的太阳辐射;ε为半球向发射率;σ为斯蒂芬-波尔兹曼常数。初始条件为:
T(x,0)=T0
(4)
式中:T0为初始温度(K)。
本文研究反问题是通过测量航天器表面温度数据反演出外热流q值。从式(3)中可看出,由于外界空间环境中引入了表征辐射热流的4次方的非线性项,大大增加了导热反问题的不适定性。因此本文提出了基于偏差原则的谱共轭梯度算法对航天器表面热流进行反演。
2 基于偏差原则的谱共轭梯度算法对外热流的反演
2.1 谱共轭梯度算法
共轭梯度法的目标函数为
(5)
其中Tcal,n为温度计算值(K);Tmea,n为温度在轨遥测值(K);n为测量温度点的数量,外热流值q=[q1,…,qn],其迭代式为
qb+1=qb+db
(6)
其中b为迭代次数;db的计算式为
(7)

(8)

(9)
由式(5)对qn求微分得到计算式
(10)

(11)
谱共轭梯度法的收敛标准可由偏差原则[16]得到。偏差原则的表述为
(12)
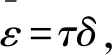
2.2 基于偏差原则的谱共轭梯度算法对热流的反演
步骤1:求解热传导方程(1)得到与测量点对应的温度值Tcal,i;
步骤3:根据温度计算值,判读是否满足偏差原则;如果满足,则停止迭代,否则,转入步骤4;
步骤4:根据公式(7)公式计算迭代方向db;
3 仿真验证与结果分析
研究对象为高度30 mm的铝合金圆柱体,圆柱体除一个端面朝向空间环境通过辐射交换热量外,其余各面均为绝热边界。因此沿轴向可视为一维导热;计算网格为沿轴向划分5个节点;热物理参数取值为密度ρ=2 700 kg/m3,比热容cp=900 J/(kg·K),热传导系数k=120 W/(m·K),辐射边界半球向发射率ε=0.6。
数值试验1给出1组吸收外热流值qmeq,如图1所示。数值试验1给出的吸收外热流曲线能够代表目前多数地球轨道航天器和深空探测航天器在轨吸收外热流变化趋势。采样取出一组离散点qn,通过求解导热正问题得到温度测量值Tmea并作为导热反问题的输入条件,采用谱共轭梯度法反演吸收外热流值qcgm。共轭梯度法迭代200次后满足停止准则,查看导热反问题反演出的温度值Tcgm与测量温度值Tmea,从图2可以看到两者符合得很好。图 3 为导热反问题反演出的吸收外热流值qcgm与真实值qmea的比较。为了更好地观察谱共轭梯度法反演结果,给出目标函数J随迭代次数的变化情况,将其与文献[15]的共轭梯度算法进行对比,对比结果如图4所示。从对比的结果可以看出,本文提出的谱共轭梯度算法可以加快算法的收敛速度,减少迭代次数。

图1 吸收外热流曲线

图2 温度反演值与测量值的比较
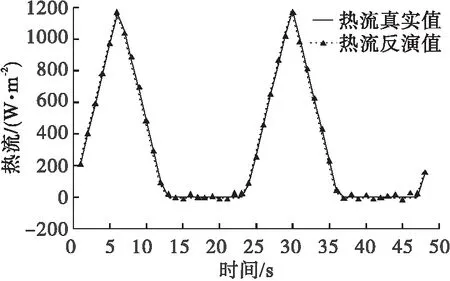
图3 数值试验1的吸收外热流反演值与真实值比较
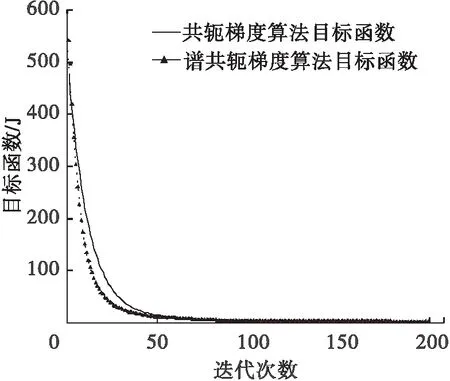
图4 目标函数J随迭代次数的变化情况
为了验证算法消除不适定性的性能,在测量值Tmea上加入2%的误差,再次反演出新的外热流值qerr,并与真实值qmea做比较,其比较结果如图5所示。将求出与qmea的相对偏差的绝对值,在图6中给出。最终得出当测量值中加入2%的测量误差后,反演值与真实值的最大相对偏差为3.68%,表明了本文的基于偏差原则的谱共轭梯度方法能够克服反问题的不适定性。

图5 数值试验1的吸收外热流误差反演值与真实值比较

图6 反演热流qmea值的相对偏差
4 结论
本文研究了航天器设备在轨遥测温度值反演出航天器瞬态外热流的反问题方法。首先建立了反演航天器表面热流的数学模型;其次为了消除反问题的不适定性和加快共轭梯度算法的收敛速度,本文提出了基于偏差原则的谱共轭梯度算法;最后根据大多数地球轨道航天器以及深空探测航天器在轨吸收外热流的特点进行仿真实验,利用数值实验对本文的算法进行了验证。计算结果表明本文研究的方法能够反演出航天器的外热流,并且基于偏差原则的谱共轭梯度算法加快了算法的收敛速度,克服了测量误差对反演结果的不适定性。航空器外热流反演的研究,可以避免航天器热控系统故障,为研制形状稳定的相变材料的研究提供帮助。
