沟槽对湍流边界层中展向涡影响的实验研究

王 鑫, 李 山, 唐湛棋, 姜 楠,2,*

(1. 天津大学 机械工程学院, 天津 300354; 2. 天津市现代工程力学重点实验室, 天津 300350)

0 引 言

相干结构在壁湍流的产生、维持和演化发展中起着重要作用，它与壁湍流产生的高摩擦阻力密切相关[1-2]，因此如何控制相干结构是湍流减阻的核心问题，也成为近年来的研究热点[3]。

Walsh等[4-5]研究了不同类型的沟槽，发现其减阻效果依赖于沟槽的形状和尺寸，顺流向三角形沟槽的无量纲高度h+=hu*/ν<25(u*表示壁面摩擦速度，ν表示运动粘性系数)和无量纲间距s+=su*/ν<30时可以减阻，最大减阻率为8%，对应的沟槽尺寸为h+=10，s+=15；Viswanath[6]发现沟槽与流动方向一致时减阻效果最佳，偏航角超过30°时，由于边界层的局部分离，减阻效果丧失；Dean[7]总结比较了Bechert[8-9]等关于沟槽形状、尺寸与其减阻率关系的实验数据，发现三角形的沟槽具有减阻效果，但最大减阻率小于刀刃和圆齿形的沟槽。由于三角形沟槽不易损坏，加工成本低，工程应用价值大，所以成为学者研究的重点[10-12]。

湍流边界层中低速条带、喷射、扫掠、发卡涡及发卡涡包等相干结构模型的不断完善[3,13-16]以及现代实验手段的发展极大促进了沟槽减阻机理的研究。Bacher[17]发现槽谷内的流体速度较低，认为槽峰处出现了二次涡，它们既削弱流向涡对的运动，又限制低速流体的展向运动，抑制条带形成，减少了猝发事件的产生。Lee[18]使用PIV测量了沟槽面近壁的湍流结构，发现减阻状态下，多数流向涡位于沟槽之上，与槽峰作用；而增阻状态下，多数流向涡位于槽谷内，直接与沟槽表面作用，与Choi[19]数值仿真的结果一致。Suzuki[20]和Hou[21]发现减阻状态下沟槽面流场中流体的流动特征和光滑壁面相似，速度脉动和雷诺应力在近壁区减小，流向湍动能向展向的传递被抑制。王晋军[11]发现沟槽壁面流场相比光滑壁面边界层增厚，对数律区外移，流场中的低速条带比较平坦，有较好的直线性，也认为沟槽限制了流体的横向流动，增强了流动的稳定性，黄德斌[22]通过数值仿真也得到同样结论。赵志勇和董守平[23]发现槽谷内流向速度的脉动强度、高阶矩和雷诺剪应力都减小，削弱了下扫事件的强度，具有减阻效果，而槽峰与槽谷的结果相反，但是抑制程度大于增强程度，阻力总体上表现为减小。李山[12]和杨绍琼[24]发现沟槽改变了相干结构的空间形态及尺度，减少了近壁流体和外区的动量能量交换。此外清华大学的封贝贝等[10]，吉林大学的丛茜、封云[25]等均进行了沟槽减阻的研究。

总结归纳沟槽减阻的研究成果，减阻效果方面：顺流向的沟槽能降低摩擦阻力，产生减阻，实验得到了不同形状沟槽的尺寸与减阻率的关系曲线[7-9,26 ]；减阻机理方面：顺流向的沟槽峰与流向涡对相互作用，诱导产生了反向旋转的二次涡，限制了流向涡的展向运动，从而削弱了低速条带的形成和失稳，导致摩擦阻力减小[17,22]；沟槽内的低速流体，避免了槽上方流体与壁面的直接作用，增大了缓冲层的厚度，使得对数律区外移，减小了近壁区的平均速度梯度，摩擦阻力减小[11,22-23]。

Yang[27]通过PIV技术发现流向-法向平面中存在与发卡涡涡头空间隔离的相反符号的展向涡，认为其是由发卡涡涡头下方的流体减速，卷起反向剪切层产生。Hambleton[28]发现反向的展向涡一般位于顺向涡的上游下方，可能是Ω型发卡涡的涡颈(参见文献[28]的Figure 5)，Natrajan[29]的研究也支持了这个结果。Tomkins[16]认为逆向涡是发卡涡合并的印记。顺向涡和逆向涡是相干结构在流-法向平面显现出的结构形态，研究其变化规律对于减阻机理的认识非常有帮助。Wu[30]总结了展向涡在平板湍流边界层流动中的分布规律，发现顺向涡的数量随法向位置的增高而减小，逆向涡的数量出现先增大后减小的现象。沟槽的存在会对展向涡产生怎样的影响？本文采用TR-PIV (Time-Resolved Particle Image Velocimetry)技术，获得了光滑壁面与沟槽壁面湍流边界层瞬时速度矢量场的时间序列，通过分析展向涡的数量，涡的平均强度以及涡的尺度，得到了沟槽对湍流边界层中展向涡的影响规律。

1 实验

1.1 实验设备及装置

采用Dantec公司的TRPIV系统，在天津大学流体力学实验室的SZ-2型开口式循环水槽内进行实验。示踪粒子采用直径20μm，密度1.03g/m3的空心玻璃微珠，双腔激光器通过导光臂在测量流场中照射出厚度约为1mm的片光，采用SpeedSense系列相机拍摄粒子图像，相机分辨率1280pixel×800pixel，内部循环缓存为 8G，其配备远心镜头，解析度高，畸变小。实验中使用三角形顺流向沟槽壁面板，沟槽顶角为90°，槽深h=0.8mm，实验装置示意图见图1，水槽参数及实验模型尺寸详见参考文献[12]。

1.2 数据处理参数

水槽的自由来流速度控制在U∞=0.180m/s，拍摄区域大小为90mm×56mm(流向-法向)，相机采样频率为500Hz，连续模式下沟槽与光滑壁面各采集16 000张粒子图像。使用自适应互相关算法处理粒子图像，查询窗口32pixel×32pixel，重叠率75%，并进行3×3速度矢量结点的局部平均过滤，最终每个工况得到15 998个瞬时速度场。实验的其他参数见表1，表中的减阻率由光滑壁面和沟槽壁面的壁面摩擦切应力τw=ρu*2计算得到，DR=(τwP-τwR)/τwP×100%，其中ρ表示水的密度，壁面摩擦速度u*由Clauser方法得到，计算方法详见参考文献[31-32]。

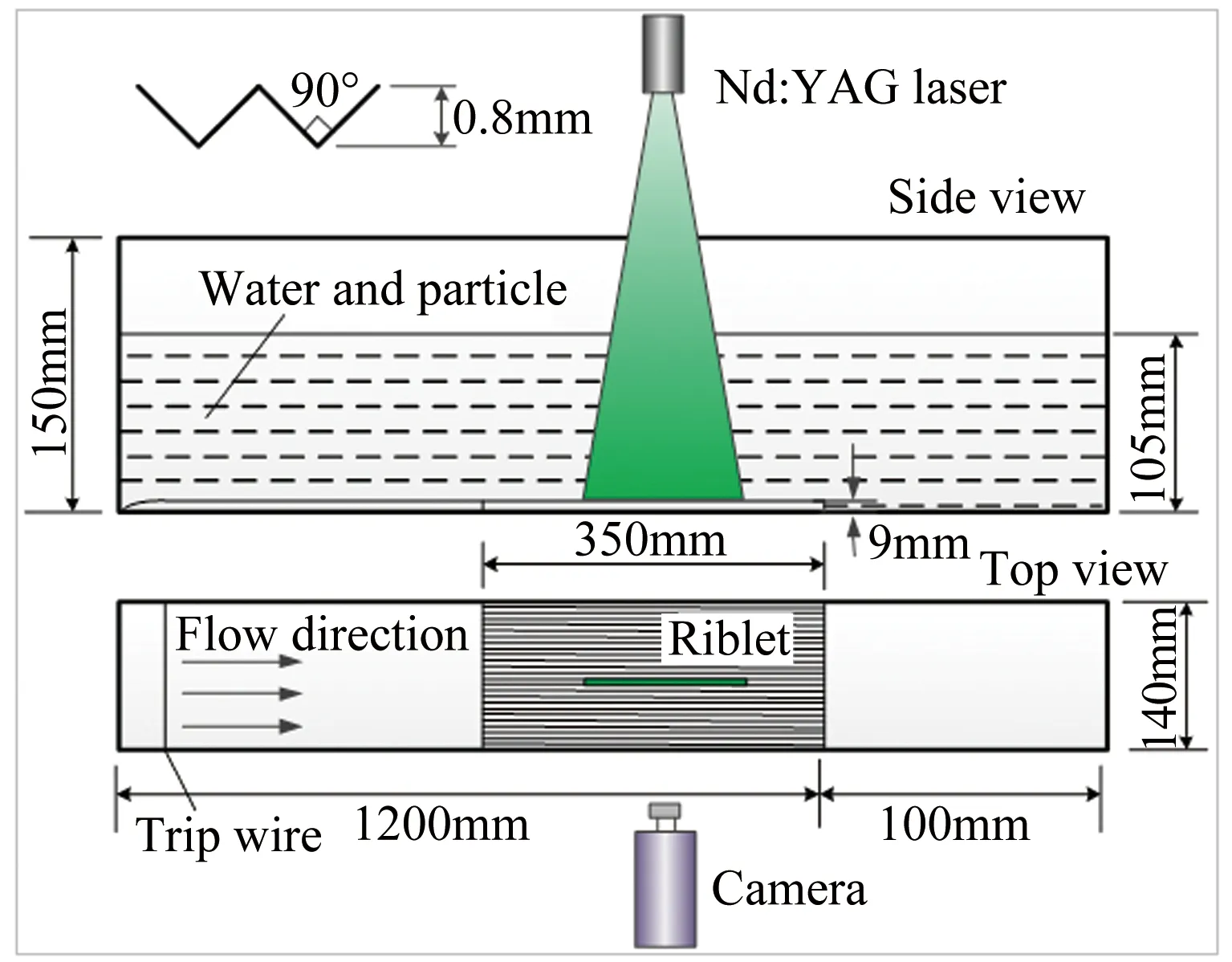
图1 实验装置示意图

表1 光滑壁面和沟槽壁面湍流边界层的流动参数Table 1 Flow parameters of the TBL over the plate and riblet surfaces

2 湍流边界层统计量

光滑壁面与沟槽壁面无量纲化的流向平均速度沿法向坐标(y+=yu*/ν)的分布如图2所示(本文的图，实心符号均代表沟槽流场结果，空心符号代表光滑壁面结果)。可以看出：光滑壁面湍流边界层的测量结果与标准平板湍流边界层对数律符合得很好，沟槽壁面近壁区的缓冲层抬升，对数律区外移，前人认为这是减阻的特征[11-12，33]。对于粘性底层的增厚和对数律区的上移通常有2种解释：(1)沟槽抑制了近壁区域的展向运动，尤其是近壁的流向涡和其相关联的喷射事件，降低了湍流的混合；(2)由于湍动能的产生和粘性耗散之间保持能量平衡，湍流强度的降低使湍动能的产生量减小，从而导致了对数律区的抬升，产生减阻。

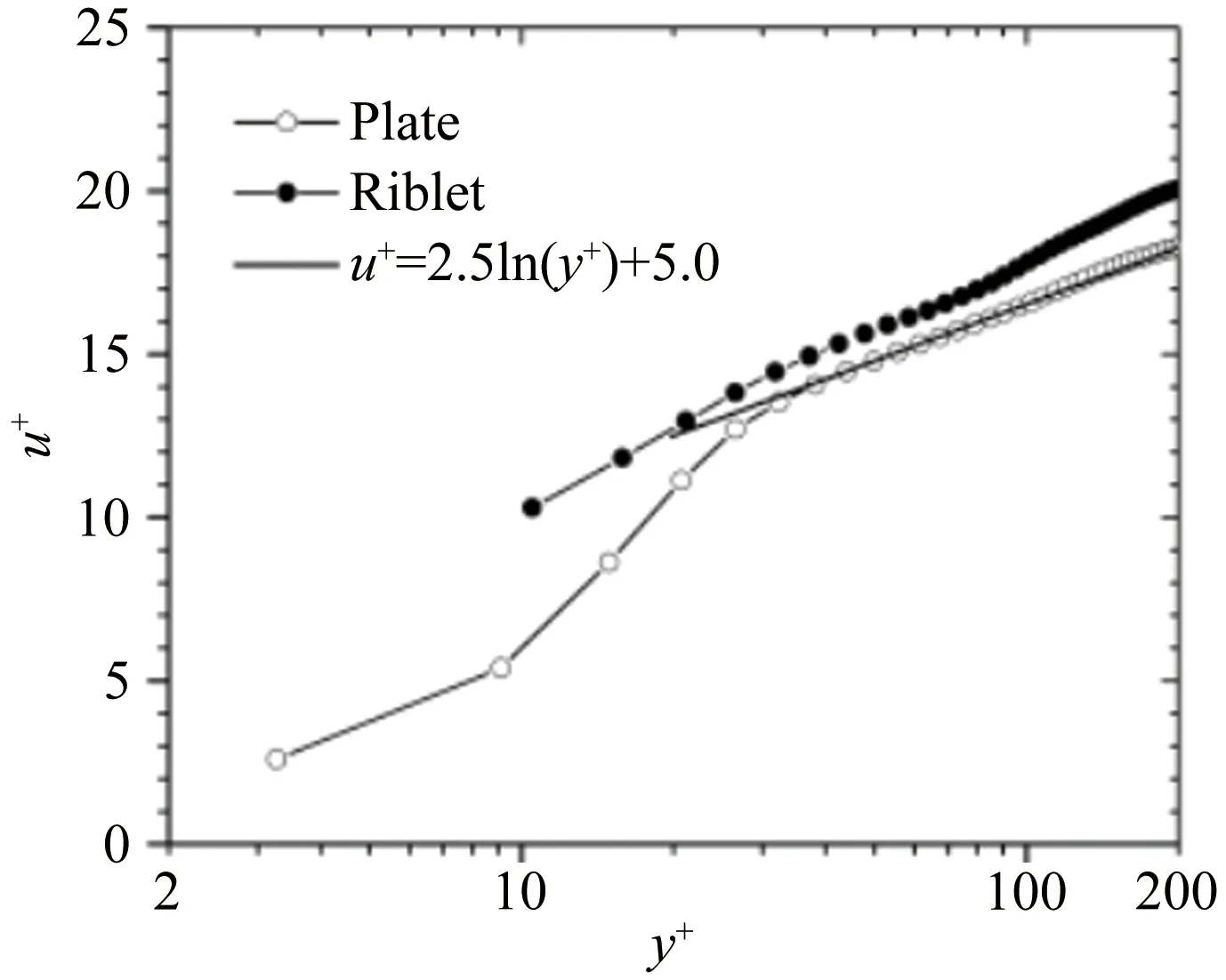
图2 光滑壁面与沟槽壁面湍流边界层平均速度剖面

2种壁面相对湍流度随y+的分布曲线如图3所示，可以看出沟槽壁面湍流强度的变化趋势和光滑壁面类似，近壁区数值有所降低，结果和前人的结论一致[19，21]，表明沟槽的存在降低了速度的脉动，使近壁区的流体变得更“安静”。

3 展向涡的分布

2D-PIV获得的流向-法向瞬时流动图像代表三维结构的纵切面，从中可以获得流场中相干结构的特征[29-30]。

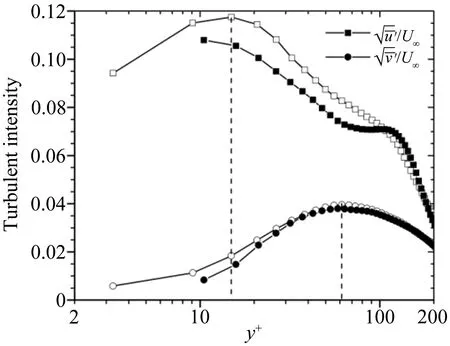
图3 相对湍流度沿法向位置y+的分布(实心：沟槽壁面，空心：光滑壁面)

Fig.3Distributionofturbulentintensityinwall-normaldirectionofTBL

3.1 涡区域的识别

展向涡是壁湍流中相干结构的主要特征，减阻机理与其有很大的关联。本文采用λci准则来识别展向涡[34-35]，此方法在许多文献中都有使用[29-30]。由于局部速度梯度张量复特征值的虚部可以代表涡的旋转强度，涡量的正负可以代表涡的旋转方向，因此通过公式(1)识别展向涡。

Λci(x,y)=λci(x,y)×sign(ωz(x,y))

(1)

其中sign(ωz(x,y))表示瞬时展向涡的符号，λci(x,y)表示瞬时展向涡的强度。

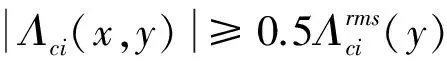
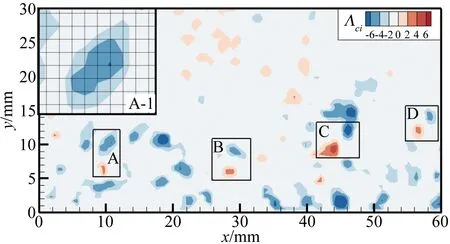
图4 2D PIV 瞬时速度场中Λci准则检测出的涡结构(蓝色为顺向涡，红色为逆向涡，A-1为A中顺向涡的局部放大图)

Fig.4Exampleofvortexidentificationandextractioninaninstantaneoustwo-dimensionalPIVvelocityfieldbyusingΛci(Retrogradespanwisevorticesarepresentedinredandprogradevorticesinblue,A-1isalocalizedenlargementofprogradevorticesinA)

3.2 展向涡的数量比例

由于涡心处的涡强大于涡的其他位置，通过寻找涡区域中涡强的局部极小值来确定顺向涡的涡心；寻找局部极大值来确定逆向涡的涡心。和Wu[30]涡密度的定义类似，定义某一法向位置处顺向涡的比例：

(2)

其中Λci为大于阈值且带符号的涡强，n表示瞬时速度场的个数，kx表示瞬时速度场中的流向网格点数。逆向涡比例的定义类似。

图5表示展向涡数量比例随y+的变化曲线(下文中的图正方形符号均代表顺向涡结果，三角形符号均代表逆向涡结果)。发现光滑壁面流场中顺向涡的比例随着法向位置的增高而不断减小，与图 4瞬时场中发现的规律一致，也与Wu[30]的结果相符合。通常认为顺向涡是发卡涡的涡头，发卡涡产生于壁面，其在离开壁面向下游运动时可能被耗散或者合并形成新的发卡涡，涡的数量减小，与Perry[15]提出的附着涡模型的合并机制以及Tomkins[16]提出的近壁尺度增长，外区合并的模型相符合。此外，顺向涡数量的减小也反应了涡向下游传播时，平均流向间距增大,与Christensen等[36]发现的发卡涡包的流向间距在外边界随法向距离的增加而增大的结论一致。沟槽壁面流场中顺向涡数量比例的变化趋势和光滑壁面类似，但在近壁区小于光滑平板，在y+=85左右位置处，数量比例曲线有个小突起，此法向位置附近沟槽的顺向涡比例大于光滑平板，在远离壁面的外区2种壁面流场中顺向涡的数量比例基本相等，说明沟槽阻碍了近壁区发卡涡的产生和发展。

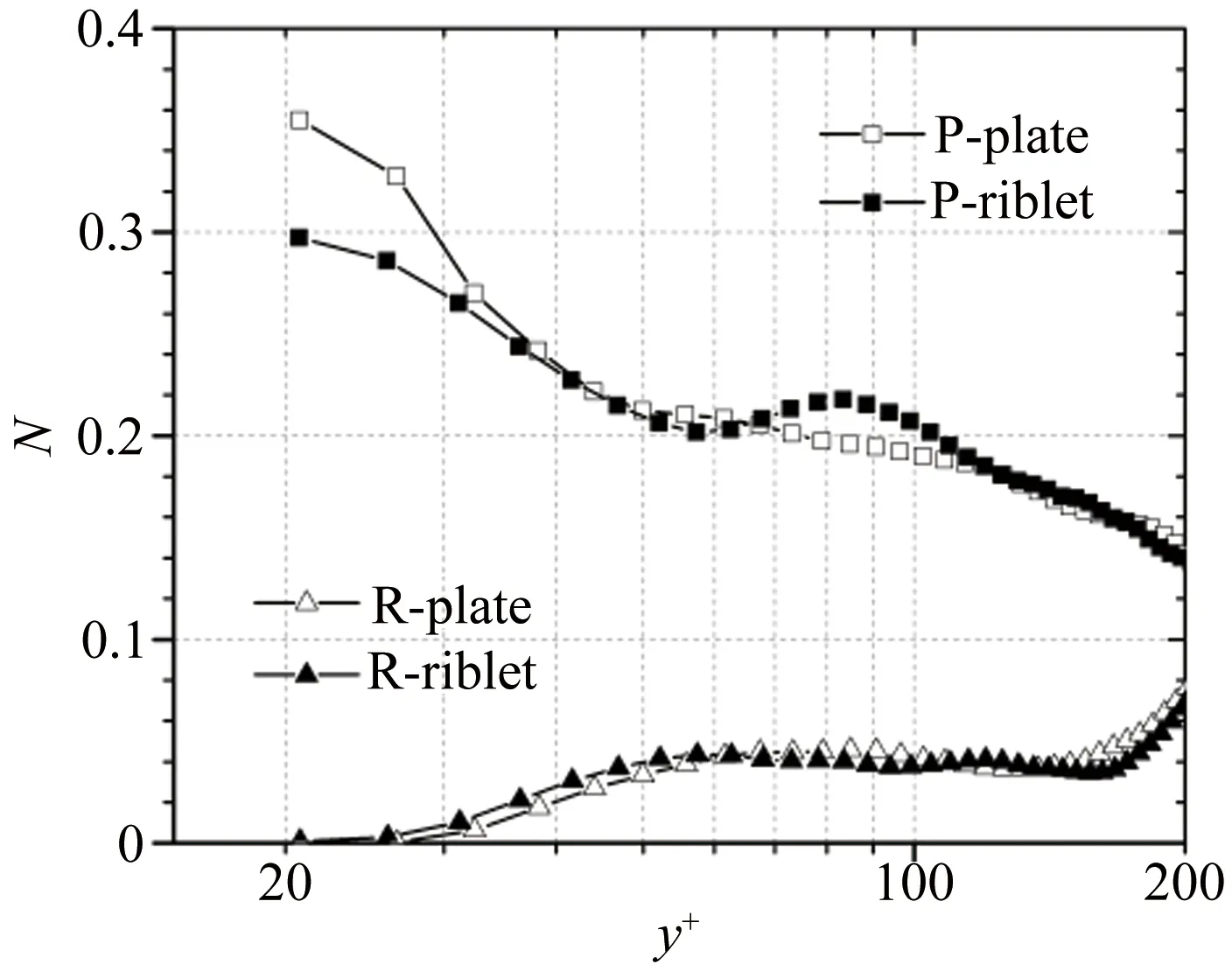
图5 顺向涡(NP)和逆向涡(NR)的比例随法向位置y+的变化

Fig.5Theproportionofprograde(NP)andretrograde(NR)vortexaccordingtoy+

从图5也可以看出光滑壁面流场的近壁区几乎不存在逆向涡，随着法向位置的增高逆向涡的数量逐渐增大，在y+=80的位置数量比例达到局部极大值，表明逆向涡与对数律区局部的湍流事件有关。逆向涡的比例明显小于顺向涡，说明以顺向涡为特征的发卡涡结构在边界层的内区占有主要作用，与图 4瞬时场中发现的规律一致。值得注意的是：在y+=150左右逆向涡的数量比例急剧增大，此结果和Wu[30]中槽道流的结果类似，应该是边界层外区受到了自由表面的影响。沟槽流场中逆向涡数量比例的变化趋势和光滑壁面类似，极大值点向壁面移动，近壁区大于光滑壁面，而对数律区小于光滑壁面。逆向涡可能是发卡涡合并或者连接的印记，沟槽流场近壁区其比例的增大，说明沟槽促进了近壁区涡结构的合并，与顺向涡数量减小的规律相符合。

3.3 展向涡的强度

将各法向位置处顺(逆)向涡的平均强度定义为：

(3)

图6为展向涡平均强度随y+的变化曲线。可以看出光滑壁面流场近壁区展向涡的平均强度大于外区，相同法向位置处顺向涡的平均强度大于逆向涡。沟槽壁面流场中展向涡平均强度的变化趋势和光滑壁面类似，越靠近壁面展向涡的平均强度差异越大，沟槽壁面近壁区展向涡的平均强度均小于光滑壁面，在外区基本相同。说明沟槽削弱了展向涡的强度，影响了发卡涡的发展和演化，影响作用主要集中在近壁区，越远离壁面对发卡涡的影响越小。

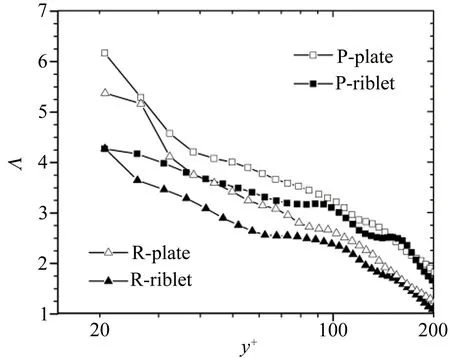
图6 顺向涡(ΛP)和逆向涡(ΛR)涡心的平均强度随法向位置y+的变化

Fig.6Averageswirling-strengthofprograde(ΛP)andretrograde(ΛR)vortexcoreaccordingtoy+

3.4 展向涡的尺度

由于流场中实际涡结构的复杂性，2D-PIV得到瞬时流场中的展向涡不规则，有可能存在偏心，加之得到的涡强度是一个离散的点场，计算涡的实际尺寸难度非常大，如图4中的A-1所示。为了分析涡尺度的分布规律，本文采用近似的方法来表征涡的尺度。图7给出了计算涡平均直径的示意图，小圆代表网格点，灰色区域代表流向-法向面实际涡的形状，涡区域之外的涡强度为零(白色小圆)，涡区域之内涡强不为零(非白色小圆)，黑色小圆代表涡强在周围几个网格取得极值(即涡心)。用圆形的直径D+(D+=Du*/ν)表征涡的尺度，当检测区域中涡强不为零的网格点占检测区域总网格数的比例大于且接近70%时，得到此矩形区域的横向和纵向网格间距(即涡的流向和法向尺度)，涡的直径定义为D=(a+b)/2，定义方法与文献[33]中的类似。例如图7中所占的比例为75%，无论增加检测矩形的长或者宽，所占比例都将小于70%，涡的平均直径为D=(3+2)/2=2.5(D+=17.475)。此外由于空间分辨率的原因，忽略了流法向都小于3个网格点的涡(即尺度D+<11.65的涡)。

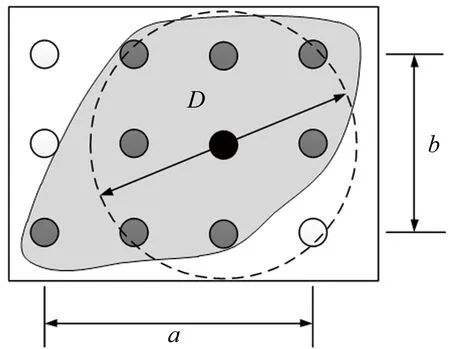
图7 涡尺度的示意图

Fig.7Anexampleofrealizingvortexdiameterfromaswirlingstrength(Λci)map

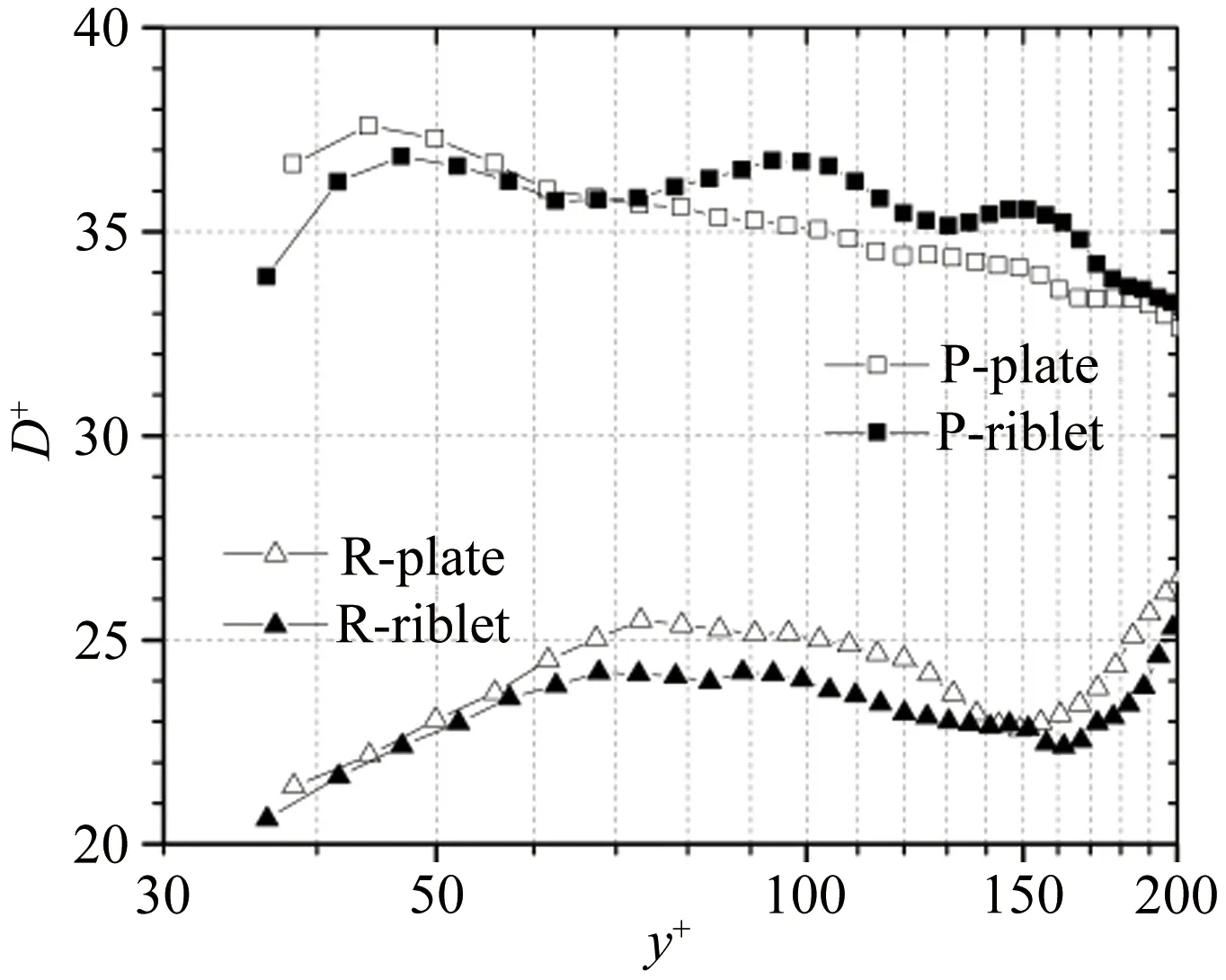
图8 顺向涡(P-D+)和逆向涡(R-D+)的平均直径随法向位置y+的变化

Fig.8Theaveragediametersofprograde(P-D+)andretrograde(R-D+)vortexaccordingtoy+

图8为展向涡平均直径随法向位置的变化曲线。可以看出顺向涡的平均直径D+随法向位置出现先增大再减小的趋势，y+=45附近顺向涡的平均直径达到局部极大值。沟槽流场中顺向涡的平均直径在36左右波动，y+<70时沟槽面流场中顺向涡的平均小于光滑壁面，符合Volino[37]得到的沟槽壁面流场中自相关函数长度减小的结论，在对数律区，顺向涡的平均直径大于光滑壁面，y+=100,150左右的2个位置达到局部极大值，这2个位置对应于图6沟槽壁面流场中顺向涡平均涡强的极大值。从图8也可以看出：光滑壁面流场中逆向涡的平均直径随法向位置的变化趋势和逆向涡数量的变化趋势相同，在y+=75左右达到极值，逆向涡的平均直径集中在24左右，明显小于顺向涡。沟槽面流场对数律区中逆向涡的平均直径小于光滑壁面，近壁区基本不变。

图9为展向涡平均流向尺度a和平均法向尺度b的比值随法向位置的变化曲线。从图9可以看出光滑壁面流场中近壁区顺向涡的流向和法向尺度比小于1，而远离壁面处尺度比接近于1，说明近壁区顺向涡的流向尺度小于法向尺度，发卡涡在向下游运动时沿法向位置抬升，越远离壁面展向涡的形状越接近于圆，符合Volino[37]使用涡旋强度自相关得到的结构形态。沟槽面流场中流向-法向尺度比值的变化趋势和光滑壁面相似，y+<60的近壁区域顺向涡的尺度比稍大于相同法向位置的光滑壁面流场，流法向尺度差异变小，而在对数律区顺向涡尺度比和光滑壁面基本相同，说明沟槽影响了湍流边界层中近壁区顺向涡的形态，对对数律区顺向涡的形态几乎没有影响。从图9也可以看出光滑壁面流场中逆向涡的平均流-法向尺度的比值随法向位置的增高而不断减小，但是始终大于1，壁面较远位置处接近于1，逆向涡的平均流向尺度大于平均法向尺度。沟槽面流场中逆向涡尺度比的变化趋势和光滑面基本类似，近壁区尺度比基本相同，y+=70～100区域中沟槽流场中逆向涡的尺度比略小于同法向位置的光滑壁面，形状更“圆”，y+=100～160的区域中逆向涡的尺度比略大于光滑壁面，形状更“扁”。

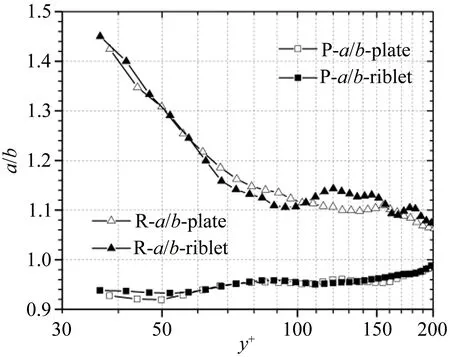
图9 顺向涡(P-a/b)和逆向涡(R-a/b)流向尺度和法向尺度的平均比值随法向位置y+的变化

Fig.9Theratiooftheaveragescaleofstreamtonormalofprograde(P-a/b)andretrograde(R-a/b)vortexaccordingtoy+

图10表示各尺度顺向涡的数量比例随法向位置的变化云图，(a)图为光滑壁面，(b)图为沟槽壁面。从图10(a)可以看出，各法向位置处顺向涡的平均直径集中在25～40，小尺度和大尺度顺向涡所占的比例较小，各法向位置处顺向涡数量比例随涡尺度的分布都呈两头小中间大的单峰结构。y+<100时，平均直径约为36的顺向涡的数量比例最大，随着法向位置的升高，平均直径的集中范围向小尺度偏移，与图8中的结果相符合。比较图10(a)和(b)，发现沟槽壁面流场中各尺度顺向涡数量比例随法向位置的变化趋势基本和光滑壁面类似，在y+=100，150的位置最大数量比例顺向涡对应的平均直径大于临近的法向位置，对应于图8沟槽壁面流场中顺向涡平均直径随法向位置变化曲线中的2个极值。分析图12(a)表示的2种壁面条件下各尺度顺向涡数量比例差值随法向位置的变化云图，发现近壁区(y+<80)小尺度涡呈红色为正值，中尺度呈蓝色为负值，说明此区域内沟槽面流场中小尺度顺向涡的数量比例增大，中尺度顺向涡的数量比例减小，而y+>80的对数律区，小尺度涡的数量比例减小，大尺度涡的数量比例增大。因此，近壁区沟槽面流场中顺向涡的平均直径小于光滑壁面，对数律区大于光滑壁面，符合图8中得出的结论。

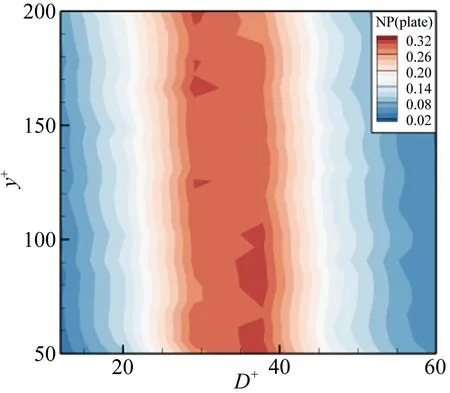
(a) 光滑壁面

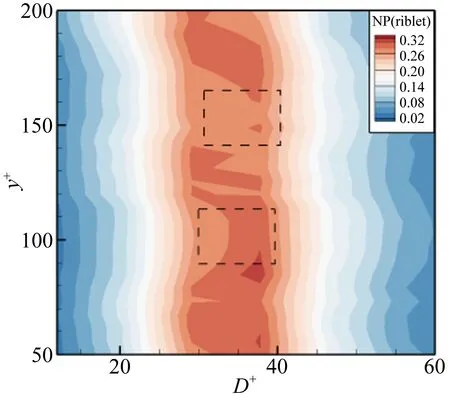
(b) 沟槽壁面

Fig.10Contoursoftheproportionofeachscaleprogradevortexaccordingtoy+

图11表示各尺度逆向涡的数量比例随法向位置的变化云图。分析图11(a)可以发现最大数量比例逆向涡的平均直径随法向位置的增高出现先增大后减小再增大的趋势，大多数逆向涡的平均直径集中在15～30之间，小于顺向涡平均直径的集中区域，各法向位置处逆向涡数量比例随涡尺度的分布呈现出靠近小尺度涡的单峰结构，逆向涡数量比例的集中范围相比顺向涡向小尺度偏移，说明各法向位置处逆向涡的平均直径小于顺向涡，与图8得到的结论一致。分析图12(b)表示的2种壁面条件下各尺度逆向涡数量比例差值随法向位置的变化云图，发现y+<65的近壁区沟槽流场内大尺度逆向涡的数量比例减小，中尺度逆向涡的数量比例增大。而y+>65的区域，小尺度逆向涡的数量比例增大，大尺度逆向涡的数量比例减小，平均直径相比光滑壁面流场变小。此外，在y+=150附近，各尺度涡数量比例差的变化幅度不明显，与图8(b)表示的平均直径的变化曲线图相一致。

通过分析，发现沟槽影响了流场中各尺度涡所占的数量比例和展向涡的形态，使近壁区小尺度顺向涡和中尺度逆向涡的数量比例增大，中尺度顺向涡和大尺度逆向涡的数量比例减小，顺向涡的平均直径变小，对近壁区逆向涡的平均直径几乎无影响，使得对数律区内小尺度顺向涡的数量比例减小，大尺度顺向涡的数量比例增大，顺向涡的平均直径变大，对数律区中逆向涡的变化趋势和顺向涡的规律正好相反。

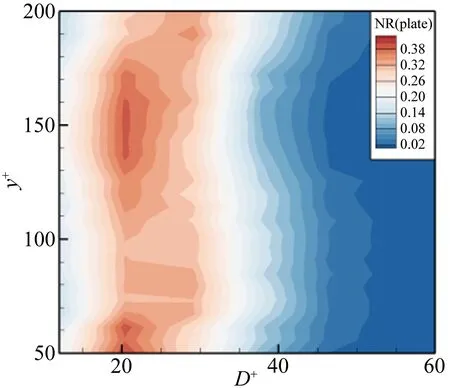
(a) 光滑壁面

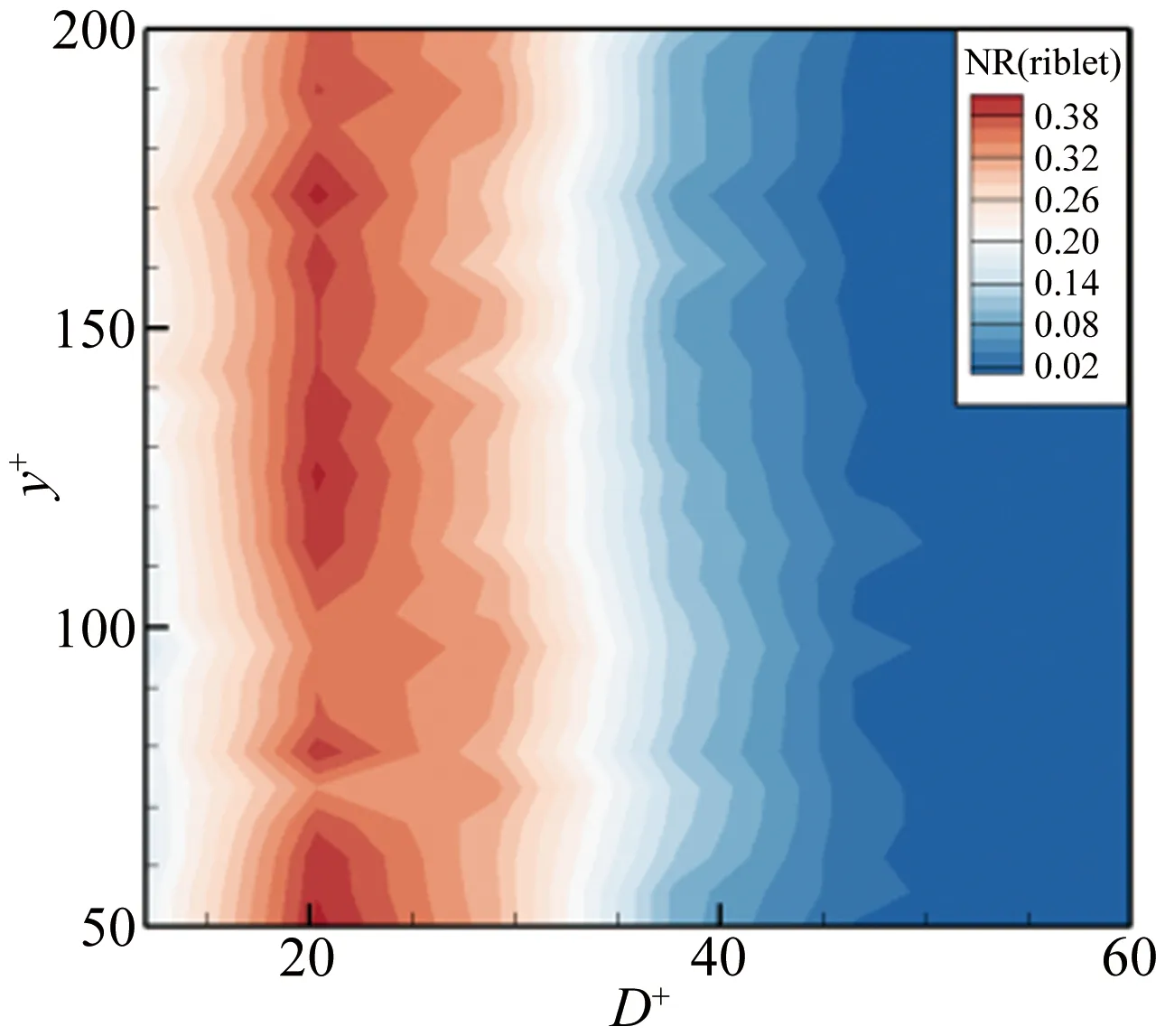
(b) 沟槽壁面

Fig.11Contoursoftheproportionofeachscaleretrogradevortexaccordingtoy+

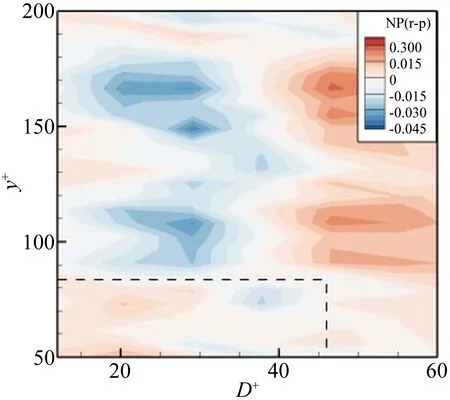
(a) 顺向涡

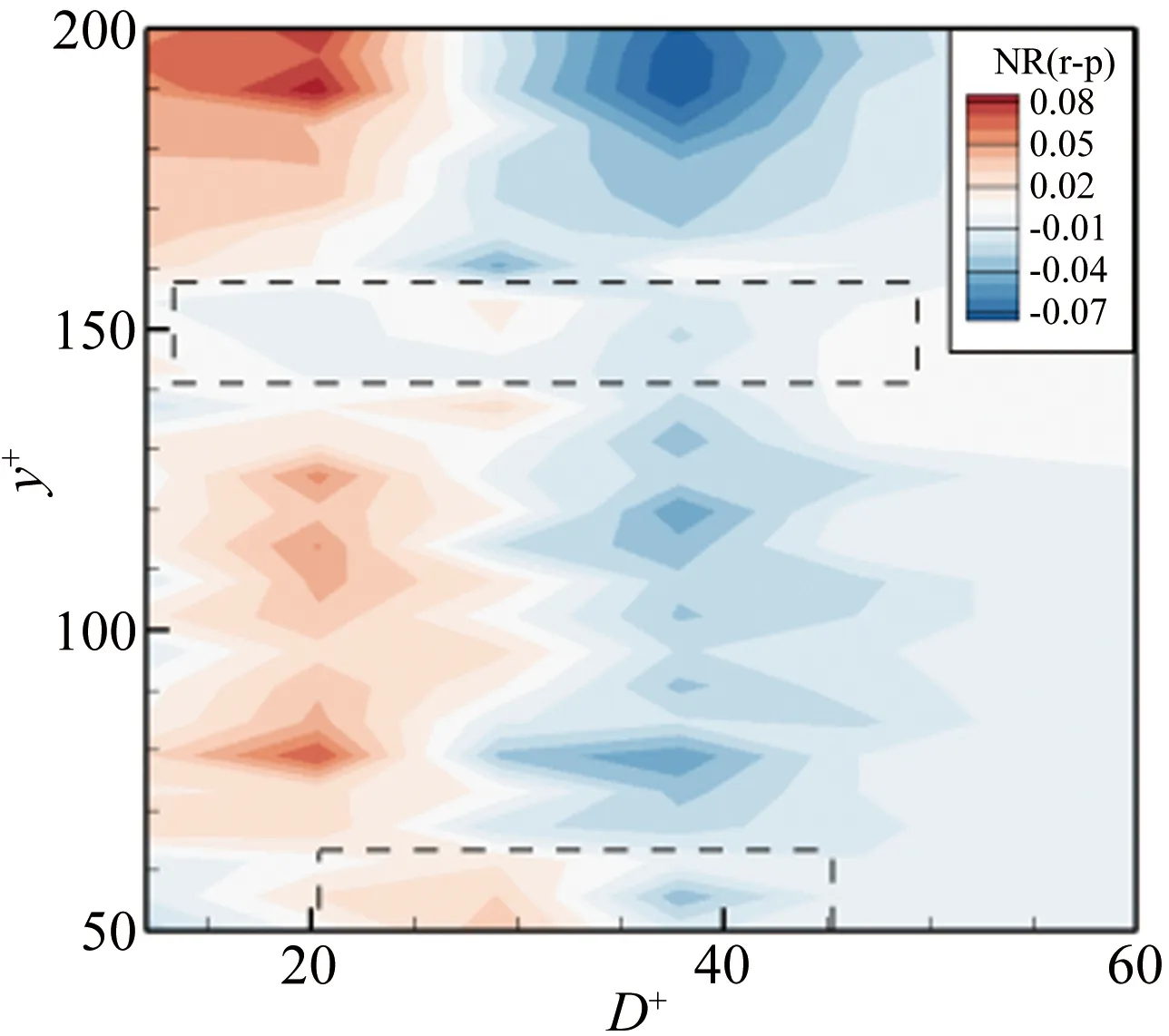
(b) 逆向涡

图12 沟槽与光滑壁面流场中各尺度涡数量比例的差值随法向位置的变化云图

Fig.12Thedifferenceoftheproportionofeachscalespanwisevortexbetweentheflowfieldoverplateandriblet

4 总 结

本文比较了光滑壁面与沟槽壁面流场的平均速度剖面、无量纲化湍流度以及展向涡的变化规律，得到以下结论：

(1) 沟槽使近壁区顺向涡的数量减小，逆向涡的数量增大，削弱了近壁区展向涡的强度，影响了发卡涡的形成和演化。

(2) 沟槽面流场中近壁区顺向涡的平均直径变小，流向-法向的尺度差异变小，对数律区平均直径增大，尺度差异基本不变；近壁区逆向涡的平均直径和尺度差异几乎不受影响，而对数律区逆向涡的平均直径变小，尺度差异变小。

(3) 近壁区小尺度顺向涡和中尺度逆向涡的数量比例增大，中尺度顺向涡和大尺度逆向涡的数量比例减小；对数律区小尺度顺向涡的数量比例减小，大尺度顺向涡比例增大，逆向涡数量比例的变化趋势和顺向涡正好相反。

[1]Kang Y D, Choi K S, Chun H H. Direct intervention of hairpin structures for turbulent boundary-layer control[J]. Physics of Fluids, 2008, 20(10): 101517.

[2]Kravchenko A G, Choi H, Moin P. On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers[J]. Physics of Fluids A: Fluid Dynamics, 1993, 5(12): 3307-3309.

[3]许春晓. 壁湍流相干结构和减阻控制机理[J]. 力学进展, 2015, 45(3): 111-140.

Xu C X. Coherent structures and drag-reduction mechanism in wall turbulence[J]. Advances in Mechanics, 2015, 45(3): 111-140.

[4]Walsh M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486.

[5]Walsh M J, Lindemann A M. Optimization and application of riblets for turbulent drag reduction[R]. AIAA-84-0347, 1984.

[6]Viswanath P R. Aircraft viscous drag reduction using riblets[J]. Progress in Aerospace Sciences, 2002, 38(6): 571-600.

[7]Dean B, Bhushan B. Shark-skin surfaces for fluid-drag reduction in turbulent flow: a review[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2010, 368(1929): 4775-4806.

[8]Bechert D W, Bartenwerfer M. The viscous flow on surfaces with longitudinal ribs[J]. Journal of Fluid Mechanics, 1989, 206: 105-129.

[9]Bechert D W, Bruse M, Hage W, et al. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry[J]. Journal of Fluid Mechanics, 1997, 338: 59-87.

[10]封贝贝, 陈大融, 汪家道. 亚音速飞行器壁面沟槽减阻研究与应用[J]. 清华大学学报(自然科学版), 2012, (7): 967-972.

Feng B B, Chen D R, Wang J D. Riblet surface drag reduction on subsonic aircraft[J]. Journal of Tsinghua University (Science and Technology), 2012, (7): 967-972.

[11]王晋军, 兰世隆, 陈光. 沟槽面湍流边界层结构实验研究[J]. 力学学报, 2000, 32(5): 621-626.

Wang J J, Lan S L, Chen G. Experimental study on the turbulent boundary layer flow over riblets surface[J]. Chinese Journal of Theoretical and Applied Mechanics, 2000, 32(5): 621-626.

[12]李山, 杨绍琼, 姜楠. 沟槽面湍流边界层减阻的TRPIV测量[J]. 力学学报, 2013, 45(2): 183-192.

Li S, Yang S Q, Jiang N. TRPIV measurement of drag-reduction in the turbulent boundary layer over riblets plate[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 183-192.

[13]Sharma A S, McKeon B J. On coherent structure in wall turbulence[J]. Journal of Fluid Mechanics, 2013, 728: 196-238.

[14] Jodai Y, Elsinga G E. Experimental observation of hairpin auto-generation events in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2016, 795: 611-633.

[15]Perry A E, Chong M S. On the mechanism of wall turbulence[J]. Journal of Fluid Mechanics, 1982, 119: 173-217.

[16]Tomkins C D, Adrian R J. Spanwise structure and scale growth in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2003, 490: 37-74.

[17]Bacher E V, Smith C R. Turbulent boundary-layer modification by surface riblets[J]. AIAA Journal, 1986, 24(8): 1382-1385.

[18] Lee S J, Lee S H. Flow field analysis of a turbulent boundary layer over a riblet surface[J]. Experiments in Fluids, 2001, 30(2): 153-166.

[19]Choi H, Moin P, Kim J. Direct numerical simulation of turbulent flow over riblets[J]. Journal of Fluid Mechanics, 1993, 255: 503-539.

[20]Suzuki Y, Kasagi N. Turbulent drag reduction mechanism above a riblet surface[J]. AIAA Journal, 1994, 32(9): 1781-1790.

[21]Hou J F, Hokmabad B V, Ghaemi S. Three-dimensional measurement of turbulent flow over a riblet surface[J]. Experimental Thermal and Fluid Science, 2017, 85: 229-239.

[22]黄德斌, 邓先和, 王杨君. 沟槽面管道湍流减阻的数值模拟研究[J]. 水动力学研究与进展, 2005, 20(1): 101-105.

Huang D B, Deng X H, Wang Y J. Numerical simulation study of turbulent drag reduction over ribelt surfaces of tubes[J]. Journal of Hydrodynamics. 2005, 20(1): 101-105.

[23]赵志勇, 董守平, 都亚男. 沟槽面对湍流边界层流动特征影响的实验研究[J]. 实验流体力学, 2004, 18(2): 59-64.

Zhao Z Y, Dong S P, Du Y N. An experimental study of turbulent boundary layer over the grooved-surface[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(2): 59-64.

[24]Yang S Q, Li S, Tian H P, et al. Tomographic PIV investigation on coherent vortex structures over shark-skin-inspired drag-reducing riblets[J]. Acta Mechanica Sinica, 2016, 32(2): 284-294.

[25]丛茜, 封云, 任露泉. 仿生非光滑沟槽形状对减阻效果的影响[J]. 水动力学研究与进展: A 辑, 2006, 21(2): 232-238.

Cong Q, Feng Y, Ren L Q. Affecting of riblets shape of nonsmooth surface on drag reduction[J]. Journal of Hydrodynamics: A, 2006, 21(2): 232-238.

[26]García-Mayoral R, Jiménez J. Drag reduction by riblets[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2011, 369(1940): 1412-1427.

[27]Yang W, Meng H, Sheng J. Dynamics of hairpin vortices generated by a mixing tab in a channel flow[J]. Experiments in Fluids, 2001, 30(6): 705-722.

[28]Hambleton W T, Hutchins N, Marusic I. Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2006, 560: 53-64.

[29]Natrajan V K, Wu Y, Christensen K T. Spatial signatures of retrograde spanwise vortices in wall turbulence[J]. Journal of Fluid Mechanics, 2007, 574: 155-167.

[30]Wu Y, Christensen K T. Population trends of spanwise vortices in wall turbulence[J]. Journal of Fluid Mechanics, 2006, 568: 55-76.

[31]Clauser F H. The turbulent boundary layer[J]. Advances in Applied Mechanics, 1956, 4: 1-51.

[32]樊星, 姜楠. 用平均速度剖面法测量壁湍流摩擦阻力[J]. 力学与实践, 2005, 27(1): 28-30.

Fan X, Jiang N. Skin friction measurement in turbulent boundary layer by mean velocity profile method[J]. Mechanics in Engineering, 2005, 27(1): 28-30.

[33]Lee S J, Choi Y S. Decrement of spanwise vortices by a drag-reducing riblet surface[J]. Journal of Turbulence, 2008, 9(23): 1-15.

[34]Chong M S, Perry A E, Cantwell B J. A general classification of three-dimensional flow fields[J]. Physics of Fluids A: Fluid Dynamics, 1990, 2(5): 765-777.

[35]Zhou J, Adrian R J, Balachandar S, et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. Journal of Fluid Mechanics, 1999, 387: 353-396.

[36] Christensen K T, Wu Y, Adrian R J, et al. Statistical imprints of structure in wall turbulence[R]. AIAA-2004-1116, 2004.

[37]Volino R J, Schultz M P, Flack K A. Turbulence structure in rough-and smooth-wall boundary layers[J]. Journal of Fluid Mechanics, 2007, 592: 263-293.