基于稀疏傅里叶变换和RSSI测距的低复杂度RSSI定位算法

王宇鹏，代 玉,王乐宁

(1.沈阳航空航天大学 电子信息工程学院，沈阳 110136；2.中国民用航空飞行校验中心 校验部,北京 100000)

无线定位通过直接或者间接测量接收到的无线电信号的到达时间、频率、到达角度等参数的变化，确定参考点与目标间的一些位置信息(如距离、方位等)，进而得到目标的位置信息(如坐标、经纬度等)。无线定位技术近年来发展十分迅速，在现实网络中已有诸多应用，例如航空干扰检测系统，仓库物品管理、游戏开发等。针对WSN(Wireless Sensor Network)的定位算法有很多，在现如今的定位算法研究中，根据是否需要测距可以将定位算法分为基于测距算法和基于非测距算法。基于测距算法是测量各通信节点之间的角度或距离等进行定位，比如基于AOA 的定位算法通过计算待测节点与锚节点所形成的夹角进行测量[1-3]；基于TOA的定位算法通过信号的传输时间来推算出节点间的距离[4-9]；基于RSSI的定位算法通过测量接收到的信号强度计算信号在传输过程中的能量损耗，推算出两个节点间的距离[10-11]。基于非测距的定位算法通过锚节点间的传递信息进行定位，比如三边测量法选取待测节点周边邻近的三个锚节点分别以其到待测节点之间的距离为半径，各锚节点坐标为圆心作圆，则三个圆相交的点即视为待测节点坐标的估计位置[12]；质心定位算法通过锚节点不断地向周边节点发送自己的坐标位置，待测节点接收到相应的信息并存储，当存储的锚节点数超过一定的阈值时连接这些锚节点形成多边形，其质心视为待测节点的估计坐标[13-15]；基于APIT的定位算法是锚节点定时广播自己位置坐标，待测节点通过与周边锚节点交换位置信息来确定这些锚节点是否会形成包含自己的三角形，从而确定待测节点的位置[16-18]。但是现如今的定位算法，都通过增加锚节点的个数来提高定位精度，并未考虑锚节点所携带信息的有效性，因此算法复杂度很高，为了解决这一问题，本文提出一种将稀疏傅里叶算法与RSSI测距相结合的定位算法来降低算法复杂度，同时保证了定位精度。

1 基于RSSI定位算法原理

RSSI即接收信号强度指示，用于指示接收信号强度的大小，主要通过测量接收无线信号的振幅大小获得。RSSI主要用于信号质量评估、信道测量、定位等应用。

1.1 RSSI测距方法

在使用RSSI测距时，主要通过计算额定发射功率与RSSI之间的强度差值计算传输损耗，之后利用路径损耗模型将路径损耗转化为相应的传输距离。本文采用对数-正态分布模型进行距离的测量，如下所示：

(1)

其中，PL(d)为无线信号传输距离为d的路径能量损耗；PL(d0)是在参考距离为d0处的能量损耗；η代表受环境因素影响的路径损耗参数，其相应的经验值一般会根据应用场景选取；X表示服从均值为零的随机变量；d0为参考距离，通常设为1 m；d为待测节点与锚节点之间的距离，则传感器节点接收到的RSSI值满足

RSSI=Pt-PL(d)

(2)

式中，RSSI为接收到的信号强度，Pt为信号发送功率，PL(d)是路径损耗。根据(2)中所得到参与定位的各锚节点RSSI值后，可按公式(3)转换为其相应的距离。

(3)

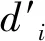
1.2 最小二乘定位方法

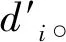
(4)

其中，ei是测量误差值，(x′,y′)是估算出的待测节点坐标，可改写公式(4)为：

(5)

待测节点的坐标同N个锚节点之间的坐标关系计算公式如式(6)所示。

(6)

公式(6)还可以转换为如公式(7)所示的矩阵形式：

QX=B

(7)

其中，Q是(N-1)*2维矩阵，X为坐标向量，B为(N-1)维向量。分别表示为：

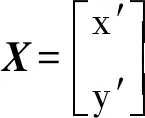
(8)

公式(8)可以转化线性最小二乘问题：

min‖QX-B‖2

(9)

则待测节点的最优坐标(x′,y′)为：

X=(QTQ)-1QTB

(10)

2 基于稀疏傅里叶和RSSI测距的低复杂度定位算法

对于无线电信号，信号在传播过程中发生反射、衍射等现象，导致锚节点接收到的信号强度可能是多路信号的叠加，从而使得测量精度降低，同时锚节点的选择对于测量精度也有一定影响。为解决上述问题，通常通过增加锚节点个数来提高定位信息的冗余度提高测量精度，如多边测量等方法。但是参与锚节点个数的增加将显著提高定位算法的复杂度及定位算法的计算时间，从而降低算法的有效性。稀疏傅里叶变换主要是对信号进行降维处理，可以充分利用信号的稀疏特性来简化传统的时频处理方法。当接收到信号后，可以将该信号经过重排、滤波和降采样后确定大值点的频率，精确估计大值点频点对应的傅里叶系数，将所确定的大值点从原信号中去除，并循环迭代之前的步骤。利用这种思想，本文通过引入稀疏傅里叶变换的方式对参与定位的锚节点质量进行预选，以降低算法的复杂度，同时保证定位精度，其基本结构如图1所示[19-20]。

图1 稀疏傅里叶变换结构示意图

图中RSSI(N)为区域内锚节点接收到的RSSI值集合，将其表示为：

(11)

N为锚节点总数，RSSIi为第i个锚节点的RSSI值，数组重排即指将所得到的RSSI值进行从大到小排序。通过滤波器g(n)滤除无用的RSSI值，如式(12)所示。

(12)

对滤波结果降采样为：

(13)

其中Ns为采样出锚节点个数。通过对锚节点的RSSI值进行稀疏傅里叶变换，采样出指定个数的最优RSSI值，然后代入到第二部分所提到的RSSI测距及最小二乘定位方法中，最终得出待测节点位置。本文所提出算法的具体实现流程如图2所示。首先设置锚节点坐标用于接收无线电信号，并记录下各锚节点接收到的信号强度RSSI值，设定一个阈值旨在接收指定数量的RSSI值，然后采用稀疏傅里叶变换采样出质量较好的RSSI值，最后采用最小二乘法对待测节点进行坐标估计，将测得的坐标值与真实坐标值进行比较，得出测量误差。

图2 算法流程图

算法的复杂程度主要由空间复杂度和时间复杂度进行衡量，本文所提出的算法主要在时间复杂度上对定位过程进行优化。在保证定位精度的同时，通过减少算法运行时间来降低复杂度。传统使用全部锚节点定位算法的复杂度为：

C传统=O(Nlog2N)

(14)

本文所提出的定位算法的复杂度为：

(15)

其中k为稀疏度。两者复杂度相除并求极限，当n趋于无穷大时有：

(16)

由式(16)可知，本文所提出的定位算法复杂度要低于传统算法复杂度。

3 性能验证

3.1 仿真参数设置

为验证本文中所提出算法的性能，本文建立了如图3所示的计算机模拟仿真环境，假设待测节点与锚节点随机分布在一个80 m×80 m的正方形区域内，其中锚节点用‘*’表示，待测节点用‘’表示。其中部署的锚节点用于接收信号得到RSSI值。仿真平台的具体参数配置如表1所示。定位误差δ可由式(17)计算。

(17)

3.2 仿真结果分析

图4～6展示了待测节点在(x=40，y=45)位置时锚节点筛选及定位结果。图5展示了使用本文中算法的定位结果，从结果我们可以看出，待测节点位置在x轴向上偏差0.101 9 m，y轴向上偏差0.106 3 m，平均偏差0.104 1 m，对应的距离偏差0.147 2 m。在图5所示使用随机锚节点筛选方法得到的结果中，可以看到待测节点在x轴向上偏差0.089 4 m，在y轴向上偏差0.618 8 m，平均偏差0.354 1 m，距离偏差0.625 2 m。对比两种方法的定位结果，发现针对这一待测节点位置，本文中所提出算法相对于随机锚节点筛选方法在坐标偏差上降低86.25%，在距离偏差上减少87.4%。

图4 挑选3个锚节点的节点分布示意图

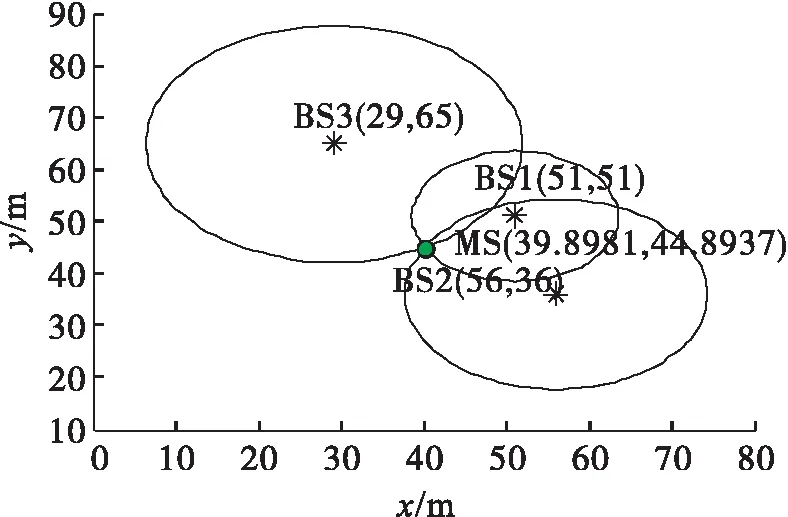
图5 文中算法的定位结果图

图6 3个随机锚节点的定位结果图

表2展示了当待测节点在待测区域内随机选择待测位置时，三种不同定位方法的定位结果分析。从仿真结果可以看出，使用全部锚节点的多边定位方法因为可使用的位置信息较多，因此定位精度最好。同时由于使用过多的参考锚节点，计算复杂度也最高，计算时间最长。使用随机筛选锚节点的定位方法减少了使用的锚节点个数，但由于筛选过程具有随机性，挑选到无用锚节点的概率很大，还需要重新筛选出性能好的锚节点进行定位，导致计算时间较长，定位精度差。而本文所提出的定位算法，在减少锚节点参与定位的同时快速筛选出合适的锚节点，大大缩短了计算时间，且定位精度相较于随机筛选锚节点的定位方法提高74.5%，相对于全部锚节点的多边定位方法下降仅42.2%。为了更好地展示本文所提出算法的复杂度情况，图7展示了在定位锚节点个数不同的情况下，使用三种不同定位方法进行定位的计算时间分析。从结果中可以看出，使用本文提出的定位算法所用时间最少，而且不会随着锚节点个数的增加而大幅度增加计算时间，由此可以看出，使用本文所提出的算法可以有效降低算法的复杂度。

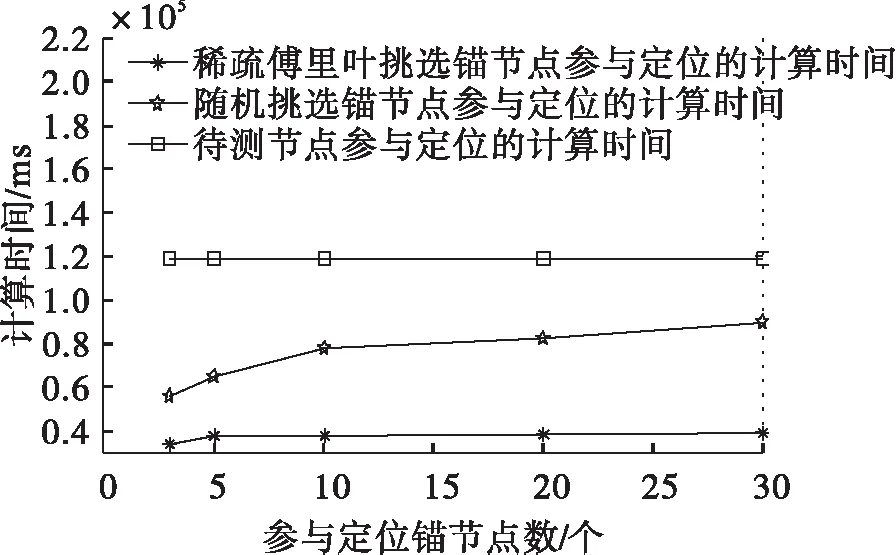
图7 不同定位方法对随机待测节点位置的定位结果计算时间比较

表2 随机待测节点位置的定位结果分析

图8所示为当待测节点在待测区域内随机选择待测位置时，在定位锚节点个数不同的情况下，使用三种不同定位方法进行定位的误差结果分析。从结果中我们可以看出，采用随机筛选锚节点定位方法及本文方法时，随着锚节点数量的增多，定位误差逐渐下降，且随机筛选方法定位误差远大于本文中提出的方法；而使用本文所提出的定位方法随着锚节点数量的增加，定位精度逐渐趋近于使用全部锚节点定位方法。由此可见，本文所提出的算法，在降低算法复杂度的同时，保证了定位精度。

图8 不同定位方法对随机待测节点位置的定位结果误差比较

4 结论

为了获得更高的定位精度，传统的RSSI定位算法需要所有的锚节点参与到定位过程中，导致计算复杂度较大。本文采用稀疏傅里叶方法，筛选出部分性能较好的锚节点进行定位计算，大大减少了锚节点的参与个数，从而降低了算法的复杂度。实验结果表明，本文所提出的定位算法，相较于传统定位算法，误差增益为42.2%，计算时间增益为68.2%；相较于随机筛选锚节点的定位方法，误差增益为74.5%，计算时间增益为41.9%。因此，本文所提出的算法在保证定位精度的同时又有效降低了算法的复杂度。