基于容栅传感器的二维微小位移测量方法研究

王睿， 李新娥， 马铁华， 杜红棉， 陆阳洋

(中北大学 仪器科学与动态测试教育部重点实验室， 山西 太原 030051)

0 引言

测试技术是信息获取的源头，微小位移测试作为新概念动态测试技术应用的一种，主要存在空间狭小、运动复杂、环境恶劣等问题[1]。目前，高精度位移测量主要有激光、光栅、线性可变差动变压器(LVDT)、容栅、时栅等[2]传感器。容栅传感器作为一种新型传感器，具有体积小、灵敏度高以及多电极平均效应提高了抗干扰能力等特点。容栅传感器的研究，欧美国家一路领先，美国雄狮公司Elite系列电容传感器线性度为0.2%(满量程)，最佳分辨率可达0.06 nm. 国内余建平等[3]研制的新型大量程x-y-θ3自由度栅式电容位移传感器非线性度维持在0.24%左右。容栅传感器可以很好地解决微小位移测量困难及空间狭小安装困难等问题，在轴转矩、转速以及星载微推进器推力测量等方面应用广泛[4-5]。

容栅传感器在微小位移测试过程中电容变化量大多在皮法级甚至更小，对测试精度要求很高。然而，容栅传感器由于栅极边缘处电场分布不均匀，产生边缘效应，导致灵敏度下降、非线性误差增大，严重影响测量精度[6-7]，测试中需要消除容栅传感器的边缘效应。

本文对容栅传感器边缘效应和二维微小位移量值和方向测量进行了研究，提出一种平面二维微小位移测量方法和二元参数模型，设计了用于二维微小位移测试的双通道测试系统，连接在两个通道上的容栅构成差动结构，提高了微小位移量值和方向的可测试性。利用带有两个千分尺的模拟测试台实际测试，实验结果表明本文提出的测量方法和参数模型可以实现平面内二维微小位移量值(毫米级)和方向的测量。

1 容栅式微小位移传感器

1.1 容栅传感器原理

容栅传感器等效于若干个平板电容并联。当忽略边缘效应的影响时，电容值为

(1)

式中：n为容栅传感器的栅条数；S为容栅两栅条正对面积；d为两栅极之间的距离；ε0为真空介电常数；εr为空气介电常数，εr=1. 当动栅与静栅在不同方向产生相对位移时，极距d或者正对面积S发生变化，容栅电容值发生相应的改变，依据电容的变化量可以测量平面微小位移。

1.2 容栅传感器边缘效应

1.2.1 容栅传感器边缘效应理论分析及仿真

对于理想的无限大平板电容传感器而言，静电场均匀分布于两极板所围成的空间，在实际应用不存在无限大平板，只有中心部分区域静电场是均匀分布，在边缘部分电场并非均匀分布，这就是边缘效应。边缘效应相当于传感器并联一个附加电容，导致传感器的灵敏度下降和非线性增加。

由于存在边缘效应，容栅传感器的实际电容值大于利用经典电容公式计算的值。其在微小位移测量中是不可忽略的关键因素，研究边缘效应常用的方法有保角变换、施瓦兹多角变换、求解电场分布的拉普拉斯方程等，其中最为精确的方法是保角变换[8]。对于梳齿状容栅来说，栅条的长度、宽度以及栅条间距不可能远大于两栅极间距，每个栅条必须同时考虑3个方向上的边缘效应，利用保角变换求解的容栅电容值为

(2)

式中：第2项和第3项为边缘效应产生的电容值；ε为介电常数；a为栅条宽度；b为栅条长度；c为栅条间距。

利用ANSYS电磁学仿真软件对未增加保护环的容栅传感器建立模型进行静电场仿真[8-9]。栅极材料为铜，介质为空气，给动栅施加1.5 V的电压，静栅电压为0 V. 仿真结果全局如图1所示，剖面如图2所示，图中E为电场强度。

图1 边缘效应仿真全局示意图Fig.1 Global schematic diagram of edge effect simulation

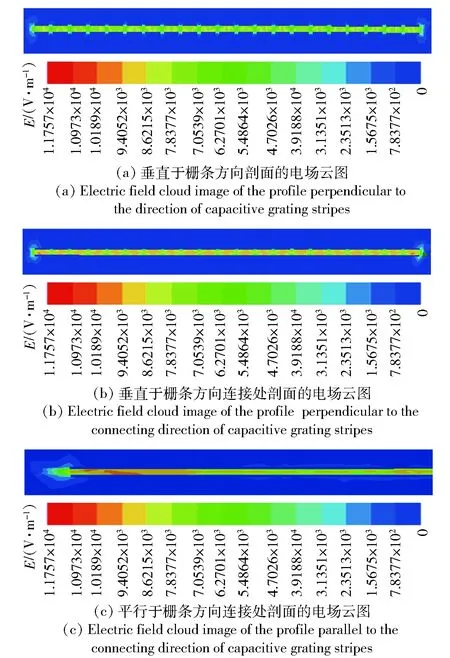
图2 容栅剖面边缘效应示意图Fig.2 Schematic diagram of edge effect of capacitive grating profile

如图1和图2所示，在容栅传感器边缘部分存在明显的不规则电场分布且数值相对较大，即容栅传感器存在严重的边缘效应，影响测试精度。考虑边缘效应的影响，容栅传感器实际电容值与栅极正对面积、介电常数、栅极间距无法呈现理论的数学关系。通过武嘉俊等[10]、王睿等[11]的研究发现，减小栅极厚度、间距和栅条间距，增大栅条宽度以及选择结构简单的传感器模型可以减小边缘效应。

1.2.2 消除边缘效应

容栅边缘效应严重影响微小位移的测试精度，可以通过设置保护环以及将容栅设计为栅极互补结构来消除边缘效应，互补栅极和原栅极电位相等使极板间的电场分布更加均匀，从而消除边缘效应造成的非线性误差。

设置保护环，即在容栅两个栅极的四周加装等位环，等位环与容栅栅极间存在很小的间隙且电位始终相等且绝缘，这样可以保证栅极边缘的电场强度均匀分布，从而克服边缘效应影响。带有保护环的容栅传感器边缘效应仿真示意图如图3所示，边缘效应可以忽略不计。

图3 带有保护环的容栅传感器边缘效应仿真示意图Fig.3 Schematic diagram of edge effect simulation of capacitive grating sensor with guard ring

对普通梳状容栅传感器，设计保护环宽度分别为1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm，并使用ANSYS电磁学仿真软件进行仿真。通过仿真发现，当保护环的宽度为2.0 mm时，随着容栅正对面积改变，容栅传感器的电容变化更趋近于线性，此时边缘效应对电容的影响最小。保护环宽度为2.0 mm时容栅电容变化如图4所示。

图4 保护环宽度为2 mm时容栅电容变化曲线Fig.4 Variation curve of capacitance of capacitive gating with the guard ring width of 2 mm

1.3 容栅传感器的结构设计

容栅传感器由动栅和静栅两个栅极组成，结构均为N个电极并联的形式，栅极之间为理想绝缘介质。容栅传感器的电容值在理想情况下只与栅极间距、栅极正对面积、栅极间相对介电常数有关，与栅极厚度无关。但是，仿真发现电容值随着栅极厚度增加而增加，为了尽可能减小栅极厚度对电容值的影响，需要将栅极厚度设计得尽可能小。经过仿真验证，设计容栅的栅极厚度为0.07 mm，栅条宽度为0.8 mm，栅条间距为0.05 mm，同时加装保护环，结构原理图如图5所示，x轴方向位移改变极距，y轴方向位移改变面积。

图5 容栅传感器结构原理图Fig.5 Schematic diagram of capacitive gating sensor

1.4 容栅传感器的静态特性

1.4.1 灵敏度

灵敏度为传感器在稳态下输出变化与输入变化的比值，线性传感器灵敏度为静态特性的斜率，非线性传感器灵敏度为一变量。如图5所示，容栅传感器在x轴方向产生微小位移时，电容值与位移量呈反比关系，灵敏度为变量。为了方便测试，设计了适配的调理放大电路，系统输出电压值与x轴方向和y轴方向位移均呈线性关系，x轴方向灵敏度为350 mV/mm，y轴方向灵敏度为329 mV/mm.

1.4.2 线性度

如图5所示，动栅与静栅在x轴和y轴两个方向产生微小位移时，传感器电容值发生变化。利用带有两个千分尺的模拟测试台给定位移量，使容栅传感器正对面积发生改变即y轴方向发生微小位移，用电感- 电容- 电阻(LCR)表测量对应电容值，得出y轴方向实际测试曲线与拟合直线，如图6所示。

图6 y轴方向线性度曲线Fig.6 Linearity curves in y-axis direction

由线性度计算公式得

(3)

式中：Δmax是实际曲线与拟合直线得最大偏差；yFS为传感器满量程输出值。

对容栅传感器本身而言，电容值与极距呈反比关系，当两栅极极距改变即x轴方向产生微小位移时，电容值变化为非线性。为了提高测试精度，设计了合适的调理放大电路，使系统输出电压值与x轴方向和y轴方向位移均呈线性关系。

1.4.3 重复性

由带有两个千分尺的模拟测试台给定位移量，以传感器电容值刚好为0 pF时位置为初始位置，随机选取10个位置坐标点，计算每个位置对应的理论电容值，用LCR表重复5次测量每个坐标位置实际电容值并取平均值，利用贝塞尔公式计算标准偏差进而计算重复性，结果如表1所示。

表1 重复性验证

重复性测量服从高斯分布，计算公式为

(4)

式中：Ex为重复性；σ为标准偏差。

2 测试原理

2.1 x轴方向微小位移测试

如图5所示，当容栅传感器的动栅随着被测物体在x轴负方向产生微小位移时，栅极间距相应变化量为-x(正方向则相反)。由(1)式可知，电容量的变化量ΔC为

(5)

式中：C0为初始位置容栅传感器电容值。

当x/d≪1时，

(6)

略去高次项，得容栅传感器在x轴负方向产生微小位移情况下的灵敏度为

(7)

此时，输出电压值改变量为

(8)

式中：Ua0为容栅初始位置系统输出的电压值；Ua为容栅发生相对位系统移输出的电压值；G为增益；I为充放电电流；t为充放电时间。

由(8)式可知，用于小位移测量时，容栅传感器灵敏度为常数，减小初始极距d、增大容栅传感器初始正对面积S和增大栅条数n都可以提高灵敏度，但初始极距过小电容容易击穿或短路，栅条数过多趋近于平板电容丧失了容栅传感器的优点。

2.2 y轴方向微小位移测试

如图5所示，当容栅传感器动栅随着被测物体沿y轴方向移动与静栅产生相对位移时，两个栅极之间的正对面积S发生变化。容栅传感器在正对面积减小情况下的灵敏度为

(9)

式中：Δl表示y轴位移时容栅正对长度变化量；l为容栅初始位置正对长度。

此时，输出电压值的改变量为

(10)

式中：l0为容栅初始位置正对长度。

对于微小位移而言，Δl/l0≪1，则

(11)

由(9)式可知，变面积型容栅传感器的灵敏度为常数，可通过增加栅极的宽度b和减小栅极间距d(不能过小)提高容栅传感器的灵敏度。

2.3 平面任意方向微小位移测试

平面内任意方向位移均可分解为x轴和y轴两个方向的位移，x轴(改变极距)和y轴(改变面积)位移分量与传感器电容变化量存在对应关系，在电路系统中表现为电压变化量，据此建立二元参数模型方程如(12)式所示：

(12)

式中：U为平面内任意方向发生位移时通道差分输出电压值；Us为标准电容两端电压；Ur为平面内任意方向发生位移时容栅对应电压值；Ux为Ur在x轴分解量，即容栅极距改变产生的电压变化；Uy为Ur在y轴分解量，即容栅正对面积改变产生的电压变化；d0为初始极距。

3 双通道测试系统

系统实现双通道信号调理和采集，当容栅传感器分别在x轴和y轴两个方向发生微小位移时，系统两个通道输出差分电压变化趋势和量级有差别，依据两个通道输出电压变化趋势即可判别微小位移发生的方向，系统框图如图7所示。

图7 测试系统框图Fig.7 Block diagram of test system

系统采用定时采样和信号触发采样两种模式相结合实现低功耗，工作电流为17.5 mA. 标准电容以及容栅传感器由两个同向放大器组成的双运放恒流源提供恒定的充放电电流[12]。充放电过程由微控制单元输出占空比0.9的脉冲宽度调制信号控制具有T型开关配置结构、出色的关断隔离、接通条件下可以保持良好频率响应的电子开关通断而实现[13-14]，充放电信号经过差分放大后进行模拟/数字采样，采样以后的数据可以进行存储、定期读取或直接通过串口输出到上位机。差分放大器具有高共模抑制比，最大程度抑制线路噪声和线路谐波。

4 系统验证

4.1 测试方案

用带有两个千分尺的测试台模拟平面内二维微小位移，测试台上有x轴和y轴两个千分尺，分别旋动旋钮改变容栅极距和正对面积，精度均为10 μm. 在测试台固定一侧中心位置粘贴一片如图5所示容栅作为静栅，在测试台可移动一侧中心位置粘贴两片如图5所示容栅作为动栅，动栅与静栅相互平行。将动栅1和静栅连接测试系统通道1，动栅2和静栅连接测试系统通道2，如图8所示。旋动x轴方向旋钮时通道1和通道2容栅极距均发生变化且变化量相等，两测试通道差分输出电压变化量相等；当旋动y轴方向旋钮时其中一个测试通道容栅正对面积增大，另一个通道正对面积减小，相应通道差分输出电压一个增大、一个减小。

图8 测试方案原理图Fig.8 Schematic diagram of test scheme

在x轴位移测试和y轴位移测试时，以(x=2.40 mm，y=8.95 mm)为初始位置，测试台分别沿x轴和y轴正负两个方向移动0.1 mm. 平面内任意方向位移测试时同样以(x=2.40 mm，y=8.95 mm)为坐标原点移动任意距离。

4.2 测试结果及分析

为了验证测试方法是否可行，依据上述测试方案进行实际测试，测试系统及模拟测试台如图9所示。

图9 测试系统及模拟实验台Fig.9 Test system and simulation bench

以容栅极距增大方向为x轴正向，通道1相对面积减小方向为y轴正向，建立平面直角坐标系如图10所示。初始位置坐标(2.4 mm，8.95 mm)，在放大倍数为10倍情况下，通道1输出电压为7.83 V，通道2输出电压为7.05 V.

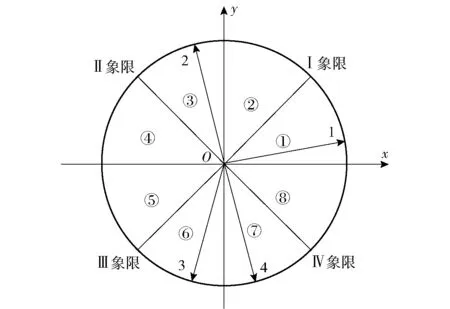
图10 坐标示意图Fig.10 Coordinate diagram

当物体在如图8测试方案所示x轴正方向产生位移时，极距增大，两个通道容栅传感器的电容值均减小，对应差分输出电压均减小，且减小的幅度相同；物体在x轴负方向产生位移时，极距减小，两个通道容栅传感器的电容值均增大，对应差分输出电压均增大，且增大的幅度相同。当物体在y轴正方向产生位移时，通道1所连接的容栅传感器正对面积减小，电容值减小，对应差分输出的电压值减小，通道2所连接的容栅正对面积增大，电容值增大，对应差分输出的电压值增大；当物体在y轴负方向产生位移时情况相反，且通道1与通道2差分输出电压改变量值相等。

综上所述，当通道1差分输出电压为U1，通道2差分输出电压为U2时，依据U1与U2的变化趋势和量值大小即可判断位移发生在如图10所示①～⑧哪个区域。

4.2.1x轴位移测试结果及分析

如图8所示，旋动x轴方向的旋钮使物体在x轴正向和负向分别产生微小位移，测试结果如表2所示。沿x轴正向发生位移时极距增大，反之减小。极距变化过程中正对面积始终保持不变。

表2 x轴位移测试结果

4.2.2y轴位移测试结果及分析

如图8所示，旋动y轴方向的旋钮使物体在y轴正向和负向分别产生微小位移，测试结果如表3所示。沿y轴正向发生位移时，通道1差分输出电压减小，通道2差分输出电压增大，沿y轴负向发生位移时则相反。面积发生变化时极距始终保持不变。

表3 y轴位移测试结果

4.2.3 任意方向位移测试结果及分析

如图8测试方案示意图所示，分别旋动x轴方向和y轴方向的旋钮使物体分别在x轴和y轴分别产生微小位移，模拟物体在平面内任意方向产生微小位移，依据参数模型求解结果结合图10位移区域分析，测试结果如表4所示。

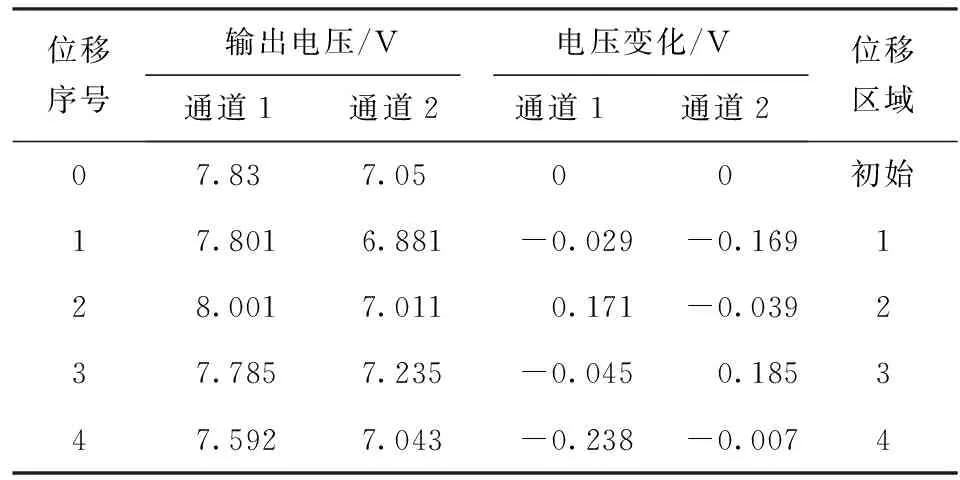
表4 任意方向位移测试结果

测试系统两通道差分输出电压值与x轴和y轴位移分量存在如(12)式所示对应关系，通过理论计算得到参数模型中常量的值，根据实测数据进行修正获得优化参数模型。利用数学仿真软件MATLAB对表4所示两通道实测电压值代入优化后参数模型进行求解，获得对应的x轴和y轴分量，求解结果存在多组解，结合如图10所示位移区域分析，得x轴和y轴分量唯一解，与模拟实验台给定实际位移分量对比如图11所示。

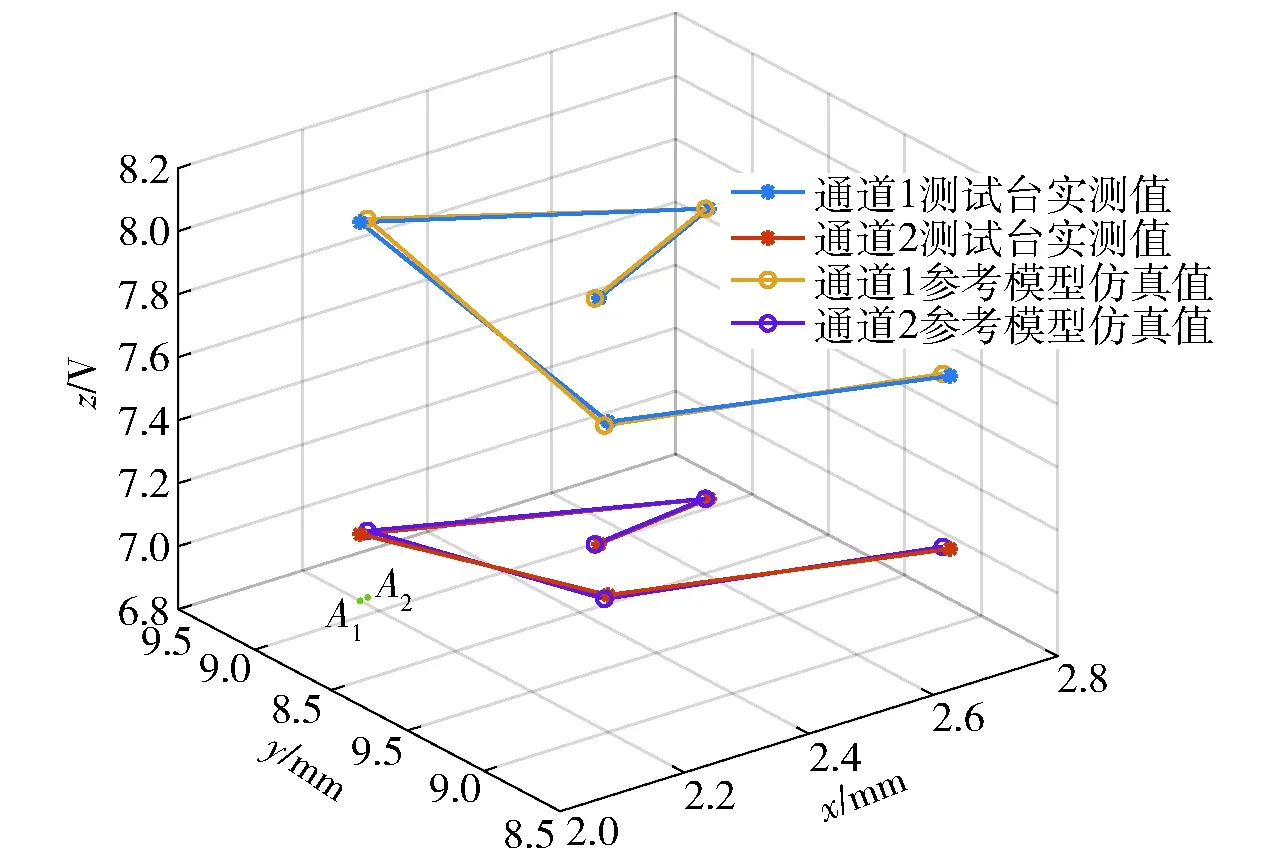
图11 模型验证结果Fig.11 Model verification results

如图11所示，A1坐标(x=2.200 mm，y=9.250 mm)为测试台给定位移坐标，A2坐标(x=2.214 mm，y=9.253 mm)为优化模型求解结果，z为通道差分输出电压值，Oxy平面内A1和A2两个点为上述点在平面的投影，为平面内任意方向位移的位置坐标点。由图11可知，对如(12)式所示参数模型优化后，位移求解结果接近实验给定位移，其中位移方向角度偏差<0.15°，量值误差<1.08%.

5 结论

本文提出了一种基于容栅传感器的二维微小位移测量方法及平面内任意方向位移二元参数模型，通过理论分析及实际测试验证了方法的可行性以及参数模型的正确性。

针对容栅传感器存在边缘效应、严重影响测试精度问题，通过对容栅传感器的原理分析以及仿真计算，对传感器结构进行优化设计，消除了边缘效应。

将优化以后的容栅传感器按图8测试方案所示平整地粘贴在模拟测试台上，并连接双通道测试系统，进行实际测试。结果表明：

1)当物体只在x轴和y轴产生位移时，本文提出的测试方法可以确定被测物体位移发生的方向和量值，x轴方向位移即极距改变时，位移实际测试值与理论计算值偏差<1.09%，y轴方向位移即正对面积改变时，位移实际测试值与理论计算值偏差<1.26%.

2)当物体在任意方向(不包括x轴和y轴方向)发生位移时，参数模型求解结果结合两通道差分输出电压变化可以确定位移方向和量值，位移方向角度偏差<0.15°，量值误差<1.08%.