物理解题中的“翻译法”

◇ 江苏 王银军

选拔性考试中的物理题的综合性都较强,一般涉及多个显性或隐性的物理情境,每一个情境都对应一个或多个方程.解物理综合题的过程就是把物理情境“翻译”成数学方程的过程.下面以两道经典例题为例进行说明.

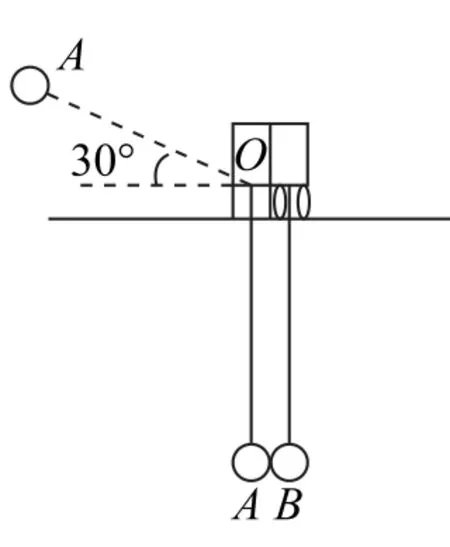
图1

例1如图1所示,在一个无限长的水平轨道上固定一个支架,在支架的中心O点处悬挂一个小球A.紧贴着支架放置一辆小车,在小车底部悬挂一个小球B.两个小球的球心在同一高度,并且相切.已知小车的质量为0.3kg,两个小球的质量都是0.1kg,球心至悬挂点的距离是0.2m.现将小球A拉到图中虚线位置(即与水平方向成30°角),从静止释放小球A,两个小球发生正碰.忽略一切摩擦和碰撞中的能量损失.求小球B被小球A碰撞后能够上升的最大高度以及小车能够获得的最大速度.

分析本题涉及A、B两球和小车.

图2

过程1：A做自由落体运动,下落高度为l＝0.2 m,满足方程垂直于绳方向的速度v1＝vcos30°,沿绳方向的速度v2＝vsin30°.

过程2：绳子绷紧过程为一个隐性的物理过程,在解题中容易被

忽略.此过程中v2减为0,v1不变.

过程3：从绳子绷紧到小球A下落至最低点的过程,满足方程代入数据得.

过程4：A和B发生弹性正碰,由于碰撞时间极短,所以我们把物理过程理想化,小车的运动忽略.这个阶段满足以下方程,

其中v′A＝0,所以.

过程5：B和小车作用的过程,小球B从最低点到摆至最高点时,小球B和小车速度相等,满足方程：

过程6：从最高点到小球B再一次回到最低点时,小车获得最大速度,考虑到解题的方便性,可与前一过程联合考虑,对小球B和小车有.代入数据得.

“翻译法”解题的一般步骤：a)明确研究对象,即涉及哪几个物体;b)明确研究对象涉及哪几个物理过程,特别是隐性的物理过程;c)针对每一过程,考虑解答计算上的方便,选用它所遵循的规律及公式;d)列方程求解.

高考是选拔性考试,试题一般涉及多个物体、多个过程,一般要对过程进行分解,把每一个过程“翻译”成方程,问题即可迎刃而解.

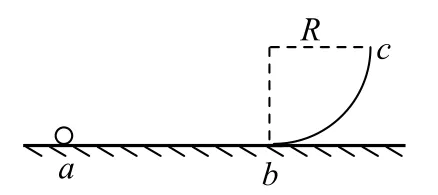
图3

例2如图3,abc是竖直面内的光滑固定轨道,ab水平,长度为2R;bc是半径为R的四分之一圆弧,与ab相切于b点.一质量为m的小球,始终受到与重力大小相等的水平外力的作用,自a点处由静止开始向右运动.重力加速度大小为g.小球从a点开始运动到轨迹最高点c,机械能的增量为( ).

A.2mgRB.4mgR

C.5mgRD.6mgR

分析过程1：从a到b做匀加速直线运动.

过程2：从b到c做变速圆周运动,以上两个过程可合成一个过程考虑.

过程3：从c到轨迹的最高点过程小球做匀变速曲线运动,可分成竖直方向和水平方向两个运动进行处理,而利用对称性解法则简单.

答案：C.

一道综合性问题一般由几个简单的过程组成.在解题时,一个十分适用的方法即按过程发生的先后顺序把现象、情境“翻译”成方程,建立现象与方程的对应关系,这样解题既规范,又清晰.