利用建模思想解决二次函数中面积问题

广东省深圳市宝安区海旺学校(518000) 陈 捷

数学模型是为解决实际问题,而对其进行抽象、化简后得出的数学关系结构.数学建模就是把实际问题抽象概括成数学模型,并对其进行求解、验证、应用的过程.数学建模是问题解决的一种重要方法和工具,是一个去粗取精,去伪存真,抽象概括的过程.数学建模思想已经广泛用于初中数学解题中,针对一类问题,给学生一个模式,让学生有据可依,以不变应万变,触类旁通,这样既符合初中学生心理特征,也有利于提高学生解决问题的能力.

1 研究必要性

查阅近年深圳市数学中考题,2016年23(3)以QD为腰的等腰ΔQDE的面积是否存在最大值?若存在,请求出这个最大值;2017年23(2)点D为y轴右侧抛物线上一点,是否存在点D使若存在,请直接给出点D坐标;2018年23(2)连接AB,交x轴于点M,交y轴于点E,抛物线与y轴交于点F.若在直线AB上有一点P,使得∠OPM=∠MAF,试求ΔPOE的面积.2019年22(3)点P为抛物线上一点,连接CP,直线CP把四边形APBC面积分为3:5 两部分,求点P的坐标.由此可以见,二次函数的面积问题在深圳中考的压轴题中成为了必考的题型,同时这也是学生失分较多,难以解决的题型.如何能帮助学生解决这一类问题呢?解决面积问题有固定的模型吗?

2 面积问题建模

2.1 在直角坐标系中求三角形面积

2.1.1 切割建模

模型一:已知点A和点B坐标,如图1所示,

垂直切割:SΔABC=DC(xA-xB)

水平切割:SΔABC=CE(yA-yB)

(注:xA表示点A的横坐标,yA表示点A的纵坐标,其他的类似.)

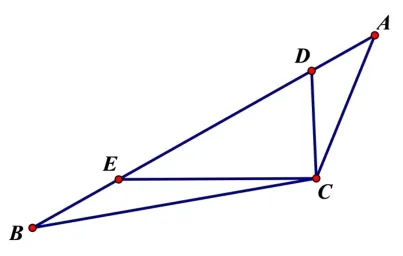
图1

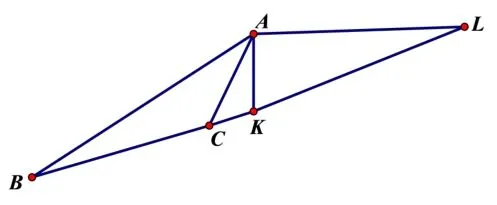
图2

模型二:已知点B和点C坐标,如图2所示

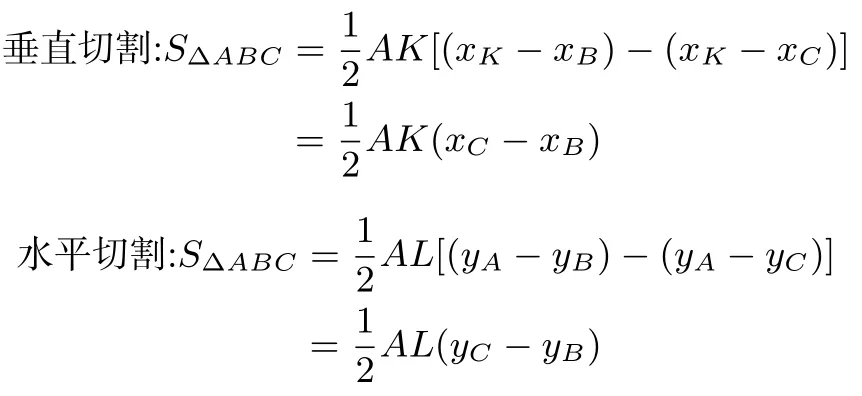
模型三:已知点A和点C坐标,如图3所示

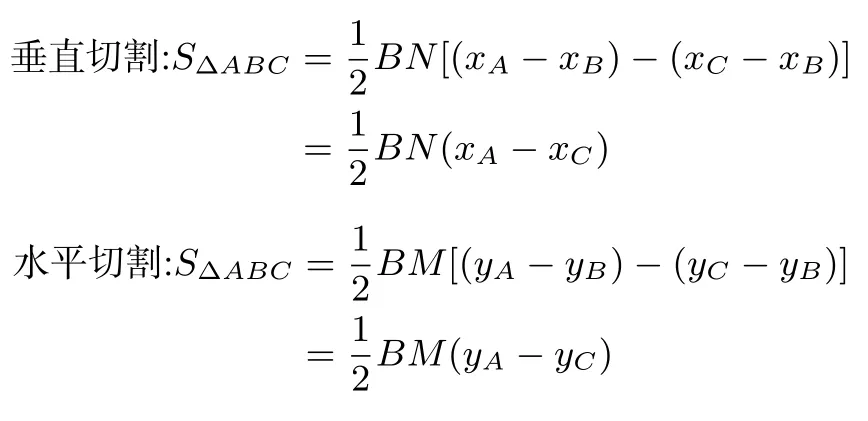
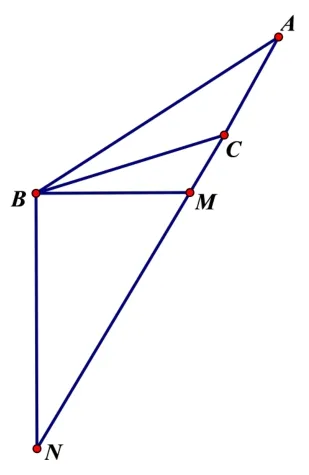
图3

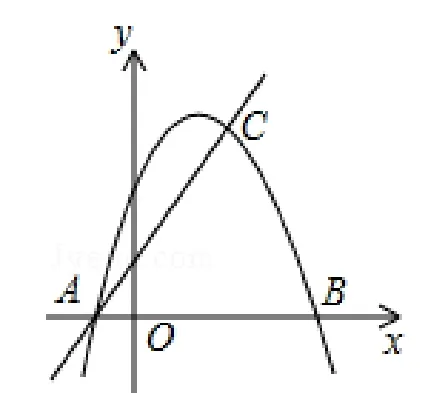
图4

2.1.2 模型应用

解:∵y=6 时,+3=6,∴x=2,C(2,6),A(-2,0),如图5,过D作DE⊥x轴交AC于点E,设

①点D在直线AC下方,

②点D在直线AC上方,

综上所示,点D的坐标为

2.1.3 应用反思

对于切割模型一,部分学生可以较好的掌握,但是对于切割模型二和三,许多同学无法掌握.因为模型一只是分割,但是模型二和三不但有分割还涉及补形,补形需要添加的辅助线较多,所以难度更大.如上面例题,看似简单,但是能解答的同学很少.学生接触模型一的题目多,习惯了过C作x轴垂线,交直线AD于点E,但是点D未知,无法表示直线AD的解析式,无法表示E坐标,也就无法表示三角形面积.究其本质,还是同学们对这三个模型没有理解好.解这类模型题的关键是:①识别三角形三个点哪两个点已知,求出这两个点连成的直线l的表达式;②过三角形的未知点作垂直或水平分割线,使分割点落在直线l上.

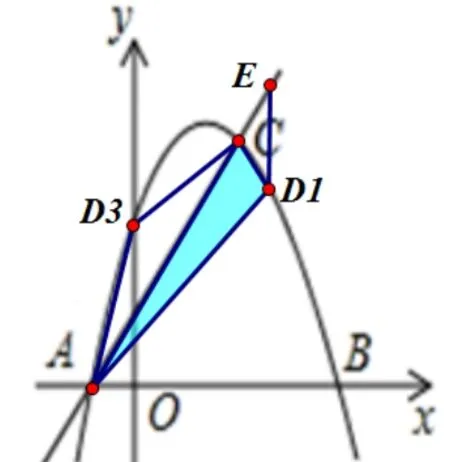
图5

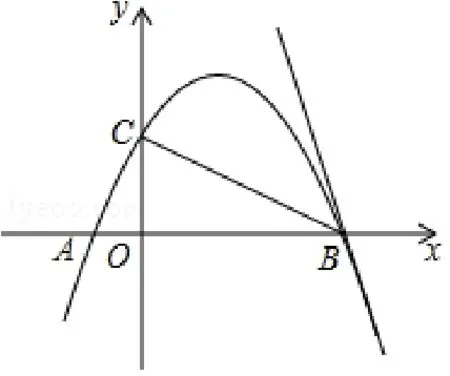
图6

2.2 面积SΔABC=kSΔABD 题型

2.2.1 两三角形有公共边的面积问题

2.2.2 模型应用

解:由题意可知C(0,2),A(-1,0),B(4,0),设D(m,n),∵SΔABC=SΔABD,∴OC=解得|n|=3,

①n=3 时,m=1 或m=2,∴D点坐标为(1,3)或(2,3);

②n=-3 时,或m=-2(舍去),∴D点坐标为(5,-3).

综上可知,存在满足条件的点D,其坐标为(1,3) 或(2,3)或(5,-3).

2.2.3 应用反思

题目出现两个三角形的面积关系,先观察是否有公共边,有公共边的都可以把三角形面积关系转化为以公共边为底边的三角形高的关系,即如应用中的例题,深圳市2017年中考题第23 题的第二问,作为一道压轴题,发现有公共边把面积关系转化为高的关系后题目思路变得清晰,做起来就不难了.

2.3 面积被分割为1:k 问题

2.3.1 两个三角形有公共高的面积问题

2.3.2 模型应用

如图7,在平面直角坐标系中,四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线AC折叠,使点B落在D处,AD交OC于E.F是过O,D,C三点抛物线的顶点,一动点P从点A出发,沿射线AB以每秒1 个单位长度的速度匀速运动,当运动时间t(秒)为何值时,直线PF把ΔFAC分成面积之比为1:3 的两部分.

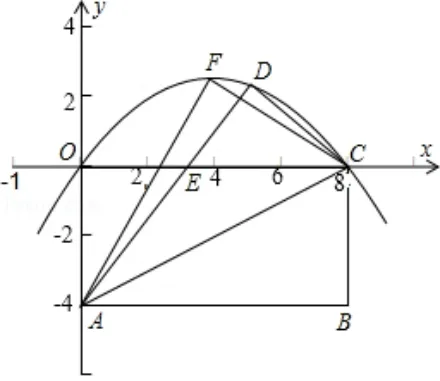
图7

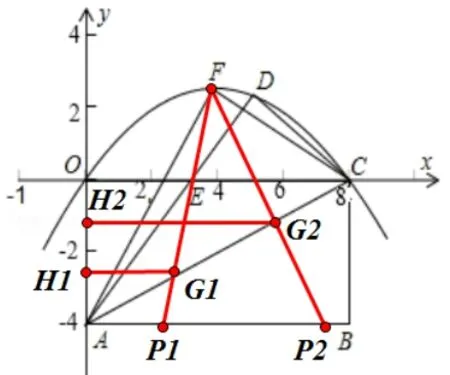
图8

解:∵y=如图8,直线PF交直线AC于点G,过G作GH⊥y轴,交y轴于点H

①∵SΔAGF:SΔCGF=1:3,∴AG1:G1C=1:3,∴AG1:AC=1:4,又H1G//OC,∴H1G1:OC=1:4,又OC=8,∴H1G1=2,又G1在直线上,∴G1(2,-3),又直线当y=-4 时,

②∵S△AGF:S△CGF=3:1,∴同理可求

综上所述:当t=或时,直线PF把ΔFAC分成面积之比为1:3 两部分.

2.3.3 应用反思

题目出现三角形面积被分割成1:k问题时,分割后两个三角形可以看成同高三角形,则面积关系转化为底边关系.如上题,题目复杂,还涉及到动点,但是识别出是这类模型后,马上就转化出AG1:G1C=1:3,再利用平行相似,把线段比例关系转化为水平(垂直)线段间的比例关系,从而解出G点,求出直线FG的表达式,题目就迎刃而解了.

2.4 面积最大值问题

2.4.1 面积最值问题转化为线段的最值问题

如图9,已知点A和点C坐标,SΔABC=DE(xC-xA),则有SΔABCmax=DEmax(xC-xA)

2.4.2 模型应用

应用:如图9,二次函数的图象经过点y=x2-2x-3,在第四象限的抛物线上是否存在一点D,使得ΔACD的面积最大,若存在求出点D的坐标.

解:∵y=x2- 2x-3,∴C(3,0),A(0,-3),∴直线AC为:y=x-3,过点D作DE⊥x轴交AC于点E,设D(m,m2-2m-3),E(m,m-3),∴DE=m-3-m2+2m+3=3m-m2,

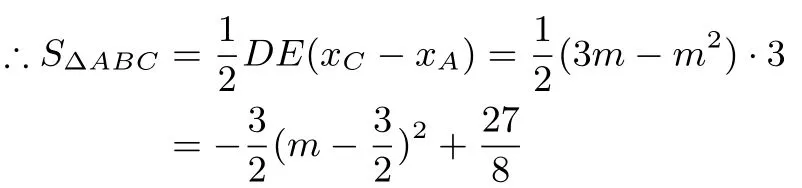
∴m=时,SΔABC最大=

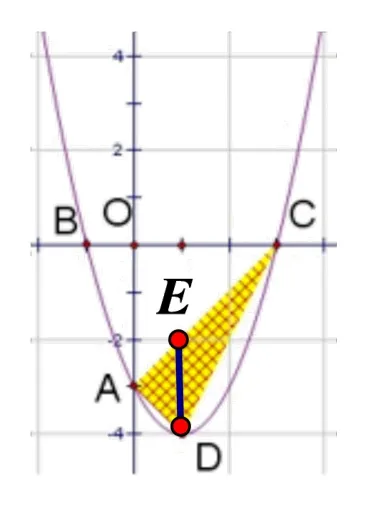
图9

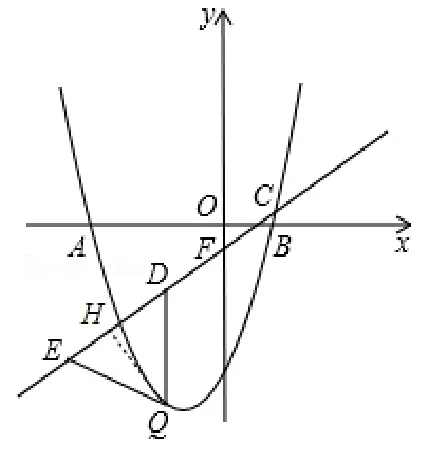
图10

应用:(2016 深圳)如图10,抛物线y=x2+2x-3 与x轴交于A、B两点,A(-3,0),B(1,0),已知直线y=分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰ΔQDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

解:如图10,作QH⊥CF,交CF于点H,∵直线CF:∵DQ//y轴,∴∠QDH=∠OFC,∴tan ∠HDQ=

设DQ=t,DH=HQ=∵ΔQDE是以DQ为腰的等腰三角形,

①DQ=DE,则

②DQ=QE,则∴当DQ=QE时ΔDEQ的面积比DQ=DE时大.

2.4.3 应用反思

已知三角形两个顶点坐标,第三个顶点在二次函数上的最值问题都可以用这个模型解决.如模型应用,这是比较典型的题目.此类型最值问题的考察在中考压轴题中比较常见,用该模型解决已经成为一种常规解法,该解法具有一般性,可推广.模型应用难度较大,没有给点坐标,但是解决问题本质是一样的,都是建立三角形面积的模型,把面积的最值问题转化为线段的最值问题.这道题抓住特殊线段DQ,利用三角函数和等腰三角形的特殊性质建立三角形面积与线段DQ关系的模型,再利用线段DQ的最值解决问题.

3 反思与总结

以上是二次函数面积问题中常见的四类问题,基础而重要,但每一种类型都可以建立一种对应的模型解决.解决这一类压轴题的关键还是要理解题意,建立解决它的模型,反思总结,再遇到相似的问题只要能识别出模型,运用模型就可以了.由此可见,运用建模思想解决复杂的二次函数面积问题可以事半功倍.在平时的解题教学中,教师应注意渗透建模思想,强化建模意识,让学生感受建模的作用,提高数学建模的能力.