阀用波纹管仿真设计建模方法及其试验验证

2020-08-12张全厚宋林红张文良于翔麟韩新博

压力容器 2020年7期

张全厚，宋林红，张文良，于翔麟，韩新博

(沈阳仪表科学研究院有限公司，沈阳 110000)

0 引言

金属波纹管作为一种弹性元件，和非金属弹性元件对比有着抗压能力强、耐高温等特点，使其广泛应用于核电、管道、传热等[1-5]领域。国内金属波纹管制造厂商常采用美国EJMA标准对波纹管进行设计。EJMA标准中关于波纹管的计算公式是应用相关变量和大量工程数据为基础进行曲线拟合得出的，所以运用此方法设计的常规波纹管应用在管路补偿器中时具有一定的可靠性，其计算精度往往能满足工程需要。但这些工程数据是以300系列不锈钢、高温合金等材料在内压工况条件下统计的，所以当波纹管在核电和航天等特殊领域用于阀门密封时(外压环境)，往往无法依靠该标准进行设计。随着计算机行业的快速发展，近些年国内外不少学者[6-9]运用有限元商业软件对金属波纹管的设计做了很多工作，同时也取得了不少成效。这为某些特殊使用要求的波纹管设计提供了方向。但大多数学者在运用有限元法对金属波纹管做仿真计算时都没有进行准确度校验，即使某些学者对仿真结果的正确性进行试验对比分析，也很少提及仿真模型的建立及其理论依据。而金属波纹管成型后由于壁厚减薄，材料会加工硬化，这对仿真几何建模和材料的设定都有影响，如果不能合理地建模则难以得出准确的结果。基于此，本文以大量工程数据为基础，提出一种阀用金属波纹管仿真设计建模的方法。

1 成型态波纹管壁厚减薄率分析

仿真分析的第一步是几何模型的建立，能否合理地建立几何模型直接影响仿真计算精度。液压多波一次成型生产的波纹管表面质量好、波形一致性好[10]，国内核电和航天领域的阀用精密金属波纹管大多采用液压成型方法进行生产。液压成型时，管坯产生了塑性变形、壁厚有所减薄，壁厚又是影响波纹管刚度、强度等的重要参数。建模时为了合理计算波纹管的壁厚减薄量，本文利用电子显微镜、工具显微镜等仪器对刨切后的波纹管进行了壁厚测量。图1为两种定型波纹管壁厚检测点的位置分布图。

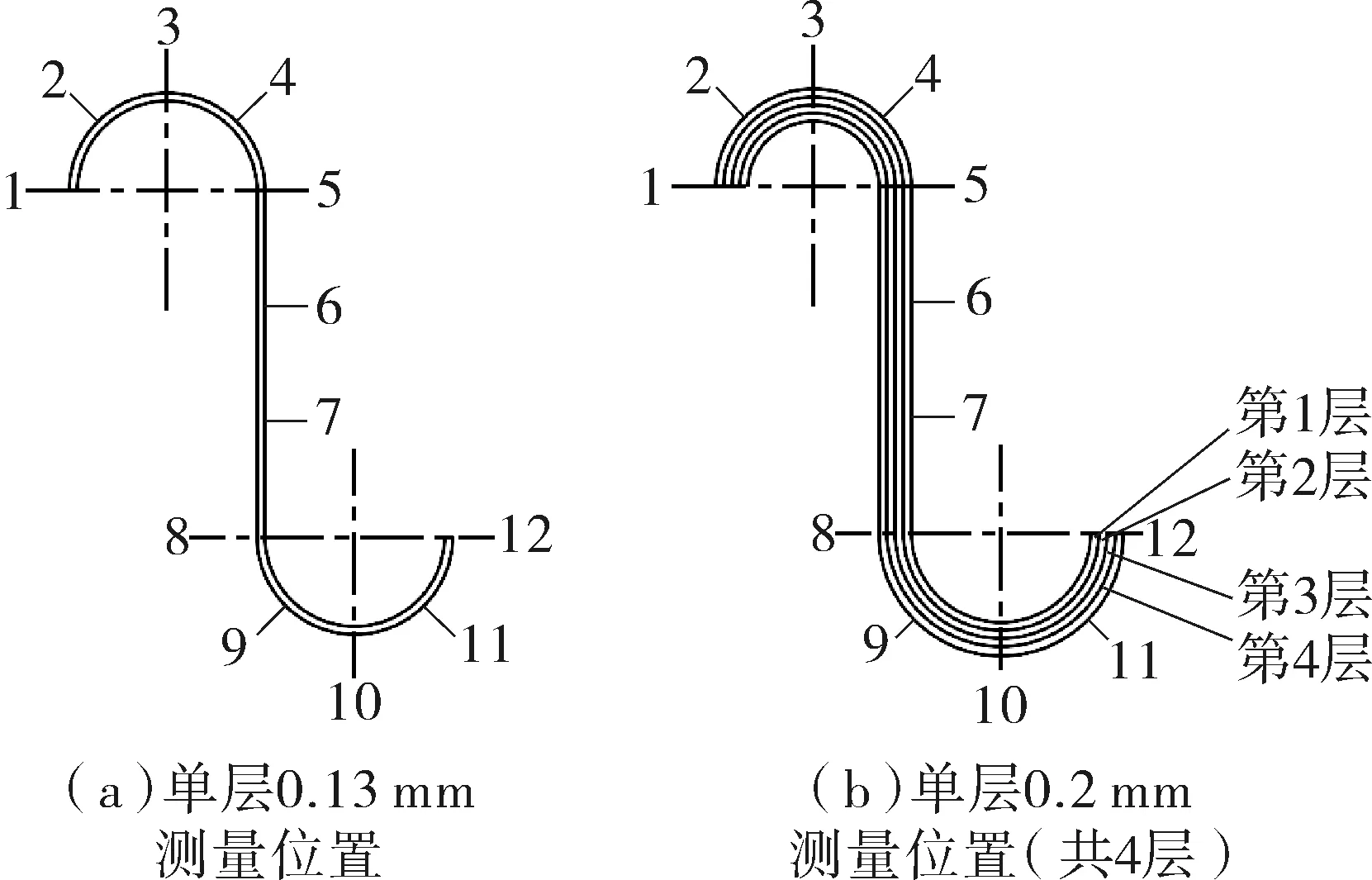
图1 波纹管壁厚测量点示意

通过对采集的数据进行整理，得到波纹管的壁厚分布图，如图2所示。

(a)单波1层

(b)单波4层图2 波纹管壁厚变化曲线

图2(a)中,单层波纹管管坯公称壁厚0.13 mm,成型压力为15 MPa;本次刨切波纹管数量为2只，分别编号为1#和2#。图中两只波纹管的壁厚都有所减薄，两组数据虽然个别点壁厚差别较大，但壁厚整体变化趋势相同。波纹管壁厚在波峰位置附近减薄量较大，平均减薄量在20%左右，个别点甚至达到30%以上。波谷位置附近出现壁厚增加情况，这不符合液压成型波纹管的制造工艺。造成这一原因是波纹管管坯的公称壁厚并不是它的真实壁厚，根据波纹管应用领域的不同，管坯壁厚公差有着不同的要求。经过和两只波纹管的真实壁厚对比，波纹管在波谷处的壁厚减薄量较小，在5%左右，个别点达到10%。环板端壁厚减薄量介于波谷和波峰之间。这和刘静等[11]的研究结果几乎一致，但由于其对管坯胀形后的波纹管壁厚测量是基于有限元仿真计算得到的，仿真时管坯壁厚一致性假设、材料的均匀性假设、波纹管成型时轴向进给速度等参数都是理想状态，所以得出的结论是壁厚均匀变化分布。郭煜敬等[12]采用有限元法对液压成型波纹管减薄率的数值模拟研究中提出，波纹管成型时不同的轴向进给速度及不同内压加载速度对成型后的波纹管壁厚减薄率都是有影响的。所以实际材料壁厚及力学性能非均匀性和超高压成型设备控制精度不高，是造成两只波纹管个别点壁厚分布偏差较大的原因。

图2(b)中，4层波纹管管坯公称壁厚0.2 mm,成型压力19 MPa；本次刨切波纹管数量为1只。和单层波纹管壁厚分布规律相似，4层波纹管各层管坯在波峰处壁厚减薄量要大于波谷处较多，但各层管坯之间壁厚减薄量大小及分布规律还是有明显区别的。造成这一现象的原因是波纹管成型后，同一测量点各层之间曲率半径不同，而且由于套管间隙等原因，很难对各层波纹管的壁厚分布做准确描述。

通过对成形态波纹管的壁厚减薄率分析可以得出，经液压胀形工艺生产的波纹管壁厚有所减薄，局部壁厚减薄率甚至达到30%以上。这要求波纹管仿真建模时壁厚减薄量应该给予考虑。同时波纹管成型时，由于材料不均、层间间隙不一致、成型设备精度限制等原因，使得难以对多层波纹管各层管坯壁厚减薄率分布进行相对准确地定量计算。

2 波纹管仿真计算几何建模方法

2.1 采用工程设计方法建模可行性分析

经过对波纹管的壁厚减薄量分析后发现，难以使用波纹管真实壁厚对其进行仿真计算。工程中根据波纹管生产工艺的不同，其生产的波纹管壁厚减薄量不尽相同，其中一种计算减薄率的方法是利用衰减率t描述管坯的壁厚变化。

t=1-hαk

(1)

式中α——波峰与波谷的半径比；

k——工艺因素影响系数。

谈卓君等[13]利用此方法对波纹管进行仿真建模计算，得到双层波纹管刚度计算误差在20%以内。对于一般工程应用，此误差可以满足大部分用户的使用要求；但当波纹管应用在航天或敏感元件领域中时，此计算精度则难以满足使用要求。而且该方法只针对双层波纹管进行试验验证分析，波纹管层数较少，导致仿真计算时波纹管层间接触设置与否对刚度值几乎没有影响，实际波纹管变形补偿时层间是存在接触的，特别是核电阀门波纹管目前已经做到6～8层，是否设置层间接触对刚度影响较大。根据任宁等[14]对Ω形波纹管进行仿真计算的研究内容，可以推断出难以利用单层波纹管刚度值与层数的乘积计算波纹管的整体刚度。以3层Ω形波纹管为例，如若按此方法计算刚度，计算误差会达到100%以上。这也和谈卓君等[13]的结论相违背。同时，谈卓君等没有说明衰减率t如何具体取值，而衰减率取值不同会直接影响刚度仿真计算的结果。所以此波纹管壁厚建模方法及结果具有局限性。

在国内工程设计时，成形态波纹管壁厚减薄量计算更多采用的是EJMA的国内转化标准GB/T 12777—2019[15]中名义壁厚的计算方法。如果运用GB/T 12777中的刚度、强度等公式设计波纹管，该方法确定的波纹管壁厚往往是可行的。但应用此方法确定的壁厚进行仿真计算则不太合理。现以标准中刚度计算公式为例进行说明。波纹管单波刚度计算公式[15]如下:

(2)

式中fiu——波纹管单波刚度，N/mm；

Dm——波纹管平均直径，mm；

Et——设计温度下波纹管材料弹性模量，MPa;

δm——成形态波纹管名义壁厚，mm；

n——层数；

h——波高，mm；

Cf——修正系数。

从式(2)中可以看出，波纹管单波刚度计算公式的自变量只有δm和Cf是人为引入的，属于估值，其他变量当波纹管定型时都可以得到相应的精确值。所以得出如下假设：式(2)中Cf的引入主要是对δm的修正。根据波纹管参数的不同，Cf值可以达到数量级的差异，fiu计算公式拟合时Cf是能对δm修正的，而仿真时还应用此壁厚计算方法进行建模，则难以得到准确的分析结果。

2.2 波纹管仿真建模方法设计

经过第1节的论述，多层波纹管成型后同一管坯各位置，以及不同层管坯的相同位置壁厚减薄量是完全不同的。所以仿真计算时要想完全依据实际情况进行几何建模几乎不可能，而且波纹管成型后存在加工硬化现象，即使可以建模但材料属性的定义也是无法实现的。所以波纹管仿真建模时还是以均匀壁厚为基础，更具有操作性和工程实用意义。由于波峰和波谷壁厚减薄量差异较大，冷作硬化强度也就不一样，建模时应将波峰与波谷的材料参数分别设置。

根据第2.1节中的论述可以得出，工程设计方法确定的成形态波纹管名义壁厚不能满足仿真的需求。本文对壁厚的处理方法是以EJMA标准中的名义壁厚为基础，通过调整波纹管壁厚使波纹管刚度仿真结果与实测结果吻合，然后得到仿真模型的名义壁厚、波纹管层数、外径等参数的样本数据库。样本数据库的建立是以公司多年积累的试验数据库为基础并结合仿真计算得到的。尽管在波纹管建模时采用参数化建模，但由于单个样本点壁厚调整时一般在3次左右，导致仿真周期较长。所以本次建立数据库样本点仅有32个，其中20个样本为300系列不锈钢材质，12个样本为Inconel 625材质，波纹管层数最多为6层。利用样本数据库，以支持向量机模型为基础，建立名义壁厚的预测模型。预测模型的输入变量能否正确选择，直接影响模型的准确度。波纹管壁厚减薄主要是由于管坯塑性变形产生的。当管坯公称壁厚确定时，波纹管内径、外径、成型压力、波峰及波谷的曲率半径是影响塑性变形的主要因素。

名义壁厚δm可由下式表示：

δm=δf(P,D,d,rc,rr)

(3)

其中：

(4)

式中δ——管坯公称厚度,mm；

P——成型压力,MPa；

D——外径,mm；

d——内径,mm；

rc——波峰曲率半径,mm；

rr——波谷曲率半径,mm；

σb——抗拉强度,MPa。

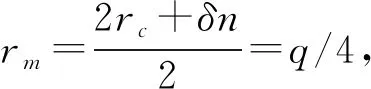
最终以公称壁厚、外径、内径、波距、波纹管层数为输入量，仿真模型名义壁厚为输出量建立预测模型。由于样本数据库的数据点较少，本文使用文献[16]中利用粒子群算法优化的最小二乘支持向量机模型进行建模，从而解决数据样本少、模型泛化能力差等问题。

3 波纹管建模方法准确性验证

3.1 仿真建模

本文以工作压力15 MPa(外压)热油阀门波纹管为算例，进行波纹管刚度和强度的仿真计算。波纹管主要参数如表1所示。

表1 波纹管参数

运用第2.2节中名义壁厚的预测模型，得到热氧阀门波纹管名义壁厚为0.205 mm。由于波纹管为几何轴对称图形，为了减小计算量，本文采用Ansys软件对波纹管进行二维模型仿真计算。图3为波纹管以单层名义壁厚0.205 mm建模后的网格划分图。

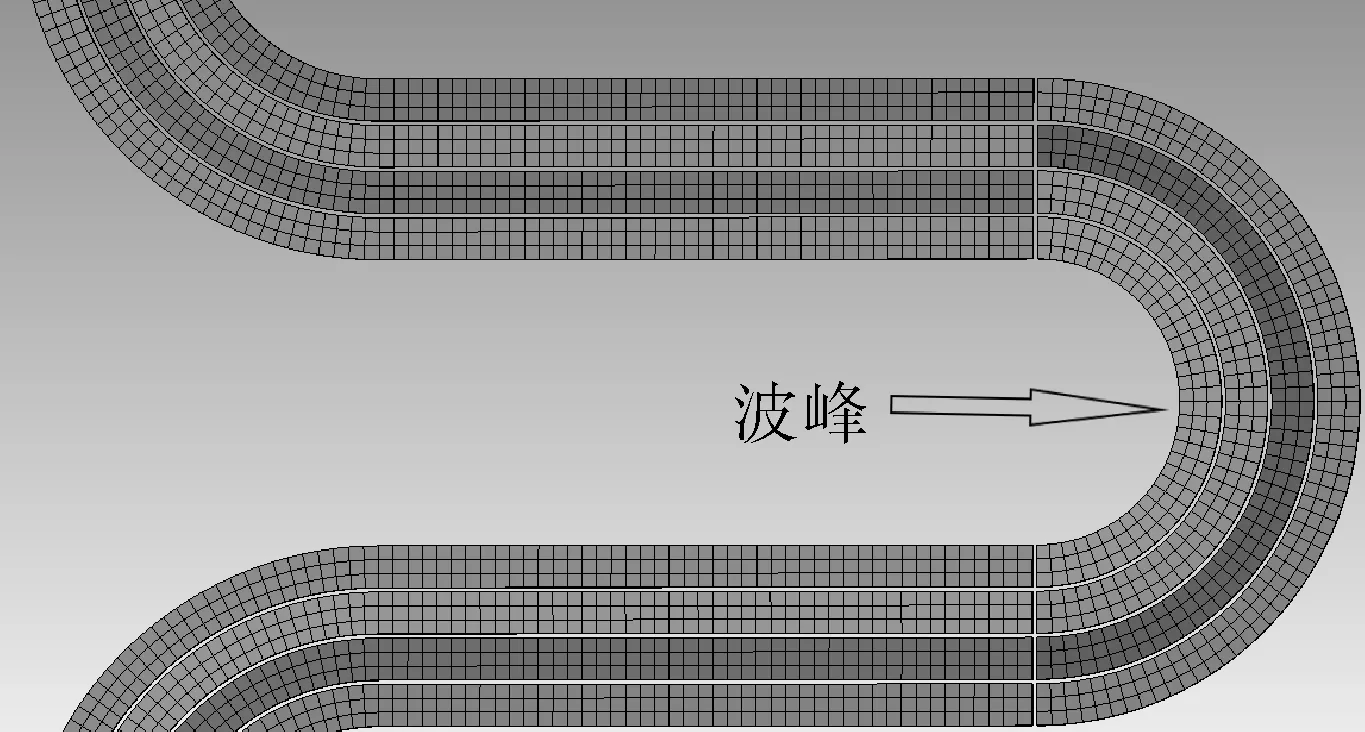
图3 波纹管网格划分

单层管坯网格划分层数为3层，波峰位置单独定义材料参数。波纹管材料参数见表2。

表2 仿真参数

材料屈服强度的取值直接影响波纹管仿真计算的强度值，对于Inconel 625材料波纹管壁厚减薄后屈服强度的取值,目前国内还没有具体的计算方法。首先采用EJMA标准中关于成形态波纹管屈服强度的计算方法。具体计算公式如下:

(5)

其中：

Cm=1.5Ysm

(6)

Ysm=f(KfFs)

(7)

Cm——材料强度系数；

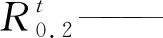
Ysm——屈服强度系数；

Kf——成型方法系数，液压成型Kf=0.6；

Fs——波纹管变形率。

Fs，Ysm具体计算公式可参考EJMA标准。

目前,波纹管仿真计算对层间接触设置类型主要分为不分离接触和摩擦接触,想要合理地选择接触类型还需结合企业自身的生产工艺及波纹管的使用环境综合考虑。图4为某5层波纹管的刨切实物图。

图4 波纹管刨切实物图

从图4中可以看出，波纹管刨切后，肉眼几乎无法观察到层间间隙，结合热氧阀用波纹管工作环境为外压15 MPa,所以波纹管实际发生位移补偿时各层管坯之间不会发生滑动。因此，本文仿真计算层间接触设置为不分离接触。波峰与环板段连接处设置为绑定接触。刚度与强度仿真计算时的边界条件和试验工况保持一致。

3.2 仿真结果分析及准确度评价

图5为波纹管压缩位移与集中力曲线图。可以看出，以EJMA标准计算的名义壁厚(壁厚0.225 mm)进行建模，仿真结果的刚度计算误差较大，为38.7%；采用预测模型的名义壁厚建模，仿真结果的刚度计算误差为9.3%。因此采用工程方法确定多层波纹管的名义壁厚进行仿真建模，往往是不可行的。

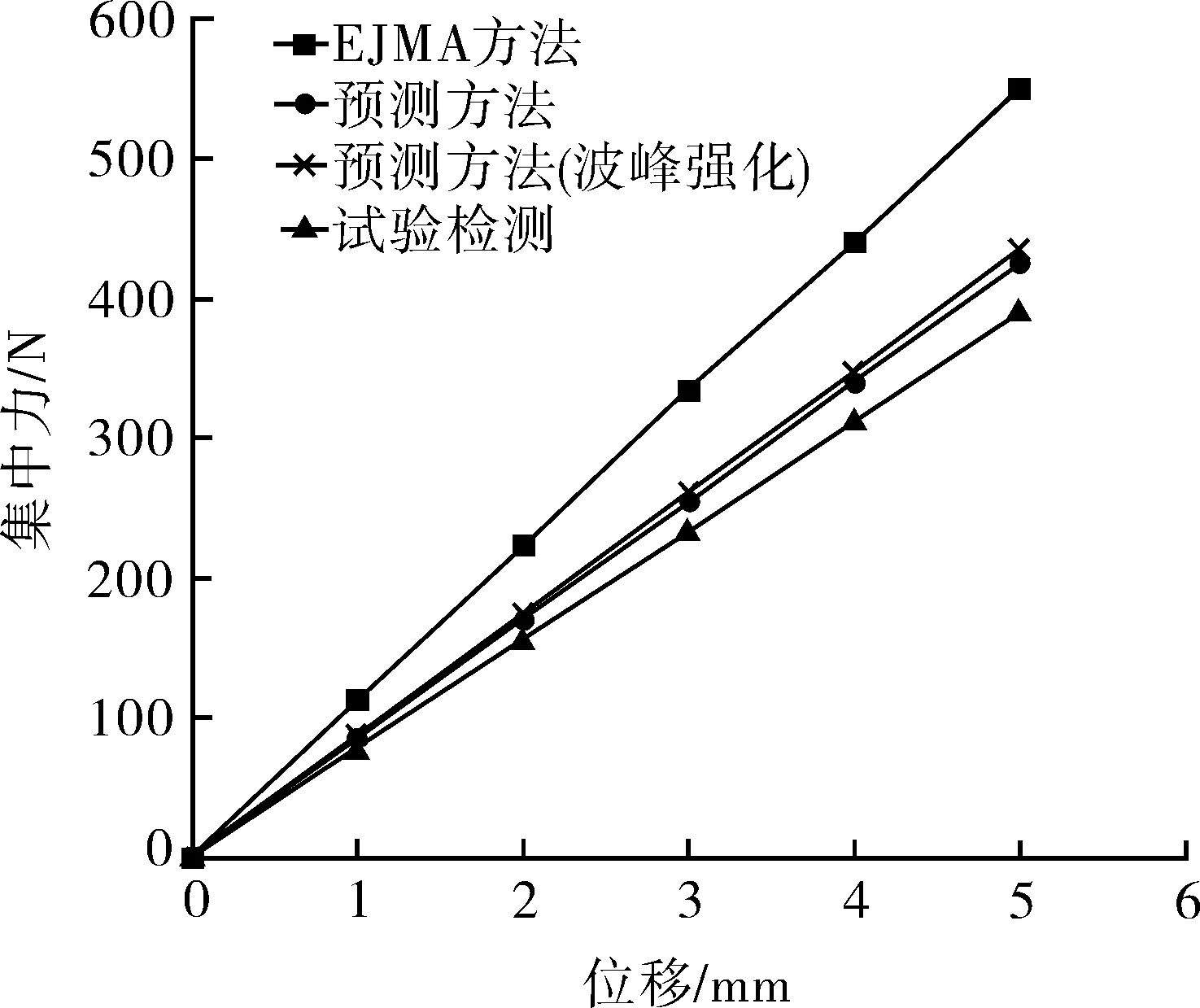
图5 压缩位移与集中力的关系曲线

在工程应用领域，波纹管刚度值的计算主要是为阀门电动执行机构选型服务的，所以波纹管刚度检测试验时压缩位移不会超过其弹性范围工作区。这也是仿真模型波峰强化与否不影响刚度仿真结果的原因。图6为波纹管压缩位移量5 mm时的应力云图，波峰局部强化模型与常规模型的应力分布趋势基本一致，波纹管局部最大应力都没有达到屈服强度。由于波峰强化模型建模时波峰与环板端并非整体，而是通过接触设置进行连接，这是造成局部最大应力存在微小差异的主要原因。

(a)

(b)图6 波纹管应力对比云图(压缩5 mm)

文中所述的热油阀门波纹管工作环境为外压工况，故波纹管失稳形式为平面失稳。为了减少计算量，采用 1/4单波几何模型进行强度仿真计算。图7为波纹管单元最大位移量与压力的曲线图。

对于无加强环波纹管，工程设计时平面失稳考核指标一般以试验前后波纹管最大波距变化率不大于15%为评定标准。从图7中可以看出，波纹管单元最大位移量在150 μm附近时，随着压力的增加、曲线斜率陡然变大。这时认为大部分单元已经进入塑性阶段，保守计算可以认为波纹管已经发生平面失稳，波峰材料无强化模型外压平面失稳压力为17 MPa,波峰材料强化模型外压平面失稳压力为24 MPa。实测波纹管失稳压力为27.5 MPa。所以波峰强化模型与非强化模型强度计算误差分别为61.8%和14.6%。由于对波纹管进行强度仿真时局部单元会发生屈服，所以波峰强化与否会直接影响强度仿真结果。图8为波纹管失稳后的变形云图，可以看出，波纹管外压失稳形式为环板段向中心压缩。