“五步教学法”提高学生问题解决能力的研究
2020-08-11王蕾
王蕾
[摘要]在小学高段问题解决教学中采取“五步教学法”:注重多样活动,激发学习兴趣;巧妙设计问题,步步释疑解惑;设计精当环节,培养解题兴趣;自主进行假设,突破解题瓶颈;大胆应用技能,自信推断结论。以此促进学生在问题解决学习中拓展思维、提升能力,为后续学习打下坚实基础。
[关键词]高段数学;问题解决;五步教学法
[中图分类号]
G623.5
[文献标识码]A
[文章編号] 1007-9068( 2020) 26-0034-03
问题解决教学是小学数学高段教学的瓶颈,大多数学生对思维含量较高的问题解决练习题容易“望题生畏”。为改变现状,笔者自2016年春季以来,在高段数学教学中关注例题、习题的思维价值,以促进学生的能力得到提升与发展,收到了较理想的效果。
一、“五步教学法”的理论依据
实用主义教育家杜威重视儿童教育,提出“生长是生活的特征,所以教育就是生长”的观点,并设计了契合儿童身心特点的“五步教学法”,可归纳为:
(1)创设课题情境:情境必须与学生的实际经验相联系,触发学生的兴趣。
(2)明确疑难所在:给予学生足够的资料,通过观察、分析、研究主题性质,明确问题所在。
(3)提出解题假设:学生提出一些尝试性的解决问题的设想,或不同的解决方案。
(4)推断假设方案:学生根据设想进行推理,求得解决问题的方案。
(5)检验行动结果:学生根据假设方案自主动手做,以检查结果是否符合设想。
“五步教学法”是一种综合性的教学方法,包含了观察、分析、综合、想象、抽象、概括等多种能力的培养和运用。它可以是层层推进,如“创设情境一提出问题一提出假设一推断假设一行动检验”,也可以独立或者二三结合,主要视学生情况和问题性质而定。
二、“五步教学法”的实践应用
笔者认为在解题教学中注重提高学生学习兴趣、培养学生积极思考的习惯,对学生的智能发展至关重要。
(一)注重多样活动,激发学习兴趣
基于学生的经验和知识能力,联系学生的生活实际创设饶有趣味的学习情境,有助于学生在多样的活动中积累丰富的经验、树立信心,进而得到多元的学习可能。例如,组织多样的主题活动,在活动中有意识地渗透和强化数学学习的内容。如在“60米对向接力赛”中切人数学思维,把运动场上的感性思维提升到数学的理性思维上。
还要注重生活化情境的积累与提炼。生活中有丰富的数学情境资源,衣、食、住、行中都蕴含了无数的数学学习的可能性。比如家庭用电问题、商场采购问题、冰箱使用问题等,需要学生有意识地观察、分析和归纳。
(二)巧妙设计问题,步步释疑解惑
如果只是反复训练解题,学生就会出现厌烦情绪,导致教学效果不佳。那么如何调动学生的兴趣,培养他们积极思考的习惯呢?这就需要教师在练习编排上下功夫,设计一些精彩的练习,让学生产生解题的冲动,激发学生的潜能。
【例1】甲、乙两位员工加工同一种零件,上午甲员工加工零件的合格率比乙员工的高,下午甲员工加工零件的合格率仍比乙员工的高。这一天中,谁的合格率高?
学生一致认为肯定是甲员工的合格率高,因为他上午和下午的合格率都比较高。我要求验证,学生很快找到了符合条件的例子(如分析①)。这时我提出了自己的想法(如分析②)。学生在半信半疑中进行演算、讨论,发现确实有可能出现乙员工的合格率高的情况。部分学生还找到了分析①中的漏洞,有了一些新的发现。最后我让学生大胆猜想还有没有别的可能,他们最终发现甲、乙两位员工的合格率还有可能相同(如分析③)。如此,学生的思维更加完善。
分析①:甲员工的合格率高
上午:甲员工加工了50个,合格率为96%;乙员工加工了40个,合格率为95%。下午:甲员工加工了50个,合格率为86%;乙员工加工了60个,合格率为85%。甲员工一天的合格率:(50x96%+50x86%)÷(50+50)=91%。乙员工一天的合格率:(40x95%+60x85%)÷(40+60)=89%。
分析②:乙员工的合格率高
上午:甲员工加工了50个,合格率为96%;乙员工加工了80个,合格率为95%。下午:甲员工加工了50个,合格率为86%;乙员工加工了20个,合格率为85%。甲员工一天的合格率:(50x96%+50x86%)÷(50+50)=91%。乙员工一天的合格率:(80x95%+20x85%)÷(80+20)=93%。
分析③:甲、乙两位员工的合格率相等
上午:甲员工加工了50个,合格率为96%;乙员工加工了80个,合格率为95%。下午:甲员工加工了60个,合格率为86%;乙员工加工了40个,合格率为85%。甲员工一天的合格率:(50x96%+50x86%)÷(50+50)=91%。乙员工一天的合格率:(60x95%+40x85%)÷(60+40)=910-/0。
学生一步步释疑解惑,在获得成功的喜悦的同时复习了百分数中经常出现的合格率等要点,不可谓不精彩。
(三)设计精当环节,培养解题兴趣
教师要设计精当的环节,培养学生的思维能力,使之融会贯通、灵活解题。
例如,“平面图形的面积”的难点是圆、正方形和三角形之间的综合运用。我在复习中采取循序渐进、环环相扣的教学策略,收到了明显的效果。
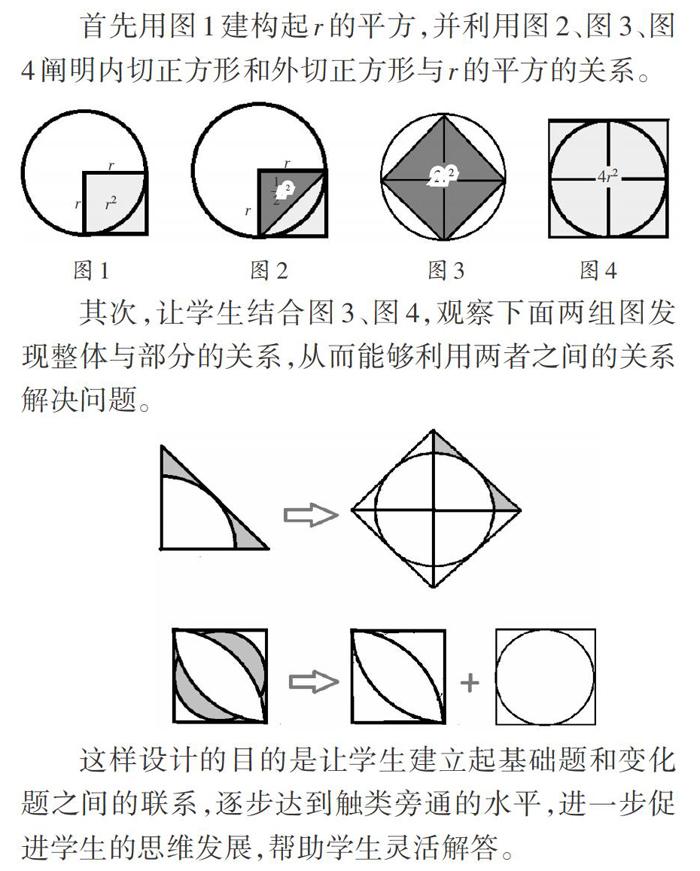
首先用图1建构起r的平方,并利用图2、图3、图4阐明内切正方形和外切正方形与r的平方的关系。
其次,让学生结合图3、图4,观察下面两组图发现整体与部分的关系,从而能够利用两者之间的关系解决问题。
这样设计的目的是让学生建立起基础题和变化题之间的联系,逐步达到触类旁通的水平,进一步促进学生的思维发展,帮助学生灵活解答。 通过这样精当的设计,绝大部分学生能够建构起圆和正方形、三角形之间的联系,能够利用基本图模型灵活解答这类几何题,在突破难点的同时也拓展了数学思维。
(四)自主进行假设,突破解题瓶颈
在毕业复习中要努力让学生经历比较精细的思维过程,学会选择合适的方法,突破解题瓶颈。
【例2】甲、乙两人分别从A、B两地同时相向而行,于E处相遇。相遇后甲继续向B地行走,而乙则休息14分钟后再继续向A地行走。甲、乙到达B、A地后立即折返,仍在E处相遇。已知甲每分钟行60米,乙每分钟行80米,求A、B两地相距多少米。
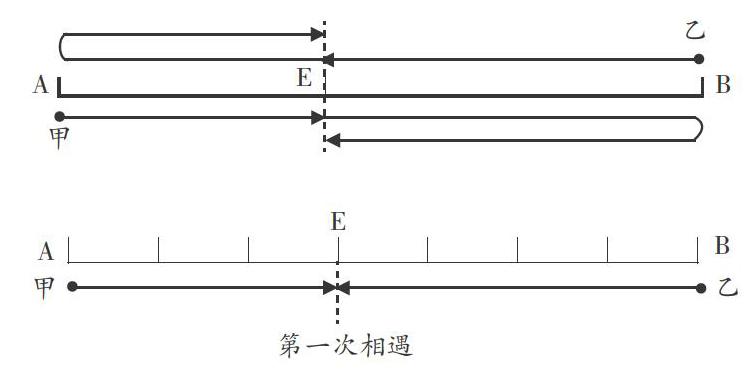
碰到这类综合性较强的题时,教师可以引导学生画图分析,并进行假设,帮助学生化繁为简、化难为易。首先是读题,让学生对题目有一个初步的理解:这是一道关于相遇问题的练习题,一共相遇了两次。可以用线段图帮助分析题意。
在第一个线段图上可以清楚地看到甲、乙两次相遇一共走了三个全程。从第二个线段图可以看出,第一次相遇时甲走了3份、乙走了4份,全程共有7份。(相遇时甲、乙所用的时间相同,因此甲、乙的速度比等于甲、乙所行的路程比:60:80=3:4)
接着,教师可以引导学生思考:从第一次相遇到第二次相遇,甲走了几份,乙走了几份?乙休息的14分钟时间里,甲走了多少米?最后,利用乙休息结束后甲、乙在E处相遇时间相同列出方程,求出每一份的路程。
解:设每一份路程为x米,那么A、B两地相距7x米。
14+6x÷80=8x÷60
7x=1680
面对这样综合性比较强的习题,学生往往无从下手。教师可以指导学生读题一画图一分析数量关系一找解题关键,帮助学生提高思维的精细性,把习题化难为易、化繁为简,发现解决问题的乐趣。
(五)大胆应用技能,自信推断结论
统计表明,学生对压轴题有一种莫名的恐惧感,勉强做出来的学生中错误率也比较高,究其原因,主要是学生缺乏自信、缺少经验、缺乏指导。要让学生树立信心,敢于接受挑战,关键需要教师的高效指导。
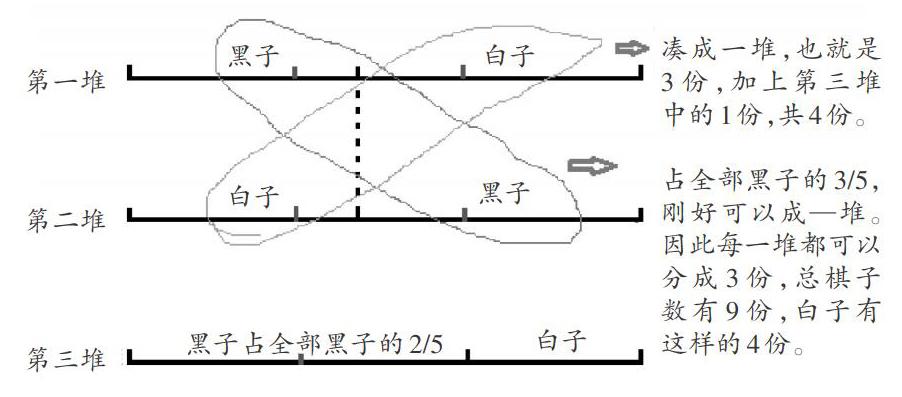
【例3】有三堆围棋子,每堆棋子数相同。第一堆中的黑子与第二堆中的白子一样多,第三堆中的黑子占了全部黑子的2/5,那么三堆棋子中,白子占了全部棋子的几分之几?
乍一看这道题条件很少,似乎很难。教师让学生不要着急做题,可以尝试画出线段图。学生发现画图之后思路就清晰了,题目瞬间变简单了,努力一下就可以“摘到桃子”,慢慢就树立了信心。
又如:
1.小明看一本故事书,看了三天后已看的页数和来看的页数之比是1:3,接着他又看了8页,这时已看的和来看的页数之比是3:5。这本故事书共有多少页?
2.601班原来男生占4/7,后来转进3人,这时男生占3/5.601班现在共有多少人?
部分学生能用找不变量、把不变量看作单位“1”进行解答,或利用不变量列方程的策略解答,但正确率不高。究其原因,主要是没有发现这两道题的共同之处,找不到更优的解题策略。我在教学时把能找到不变量的归为同一类题,尝试用比的方法解决,收到了比较理想的效果。
第一题中书的总页数是不变量,则
总页数:原来已看页数=4:1=8:2
总页数:现在已看页数=8:3
8÷(3-2) x8=64(頁)
第二题中的不变量为女生人数,则
女生人数:原总人数=( 7-4):7=6:14
女生人数:现总人数=(5—3):5=6: 15
3二(15-14)x15=45(人)
新方法优化了思维过程,简化了计算,学生的解题能力得到了很大提高,而且还能活学活用。
通过优化解题策略,帮助学生掌握精湛的解题技能,学生解题的能力提高了,碰到难题不再畏惧,敢于利用各种策略展开研究,也为后续学习奠定了良好的知识基础。
三、小结与感悟
实践证明,在数学中使用,培养并得到锤炼的精神活动,不用说是人类的精神活动,它当然也会渗透到数学以外的事实中去。对解决数学以外的问题,若巧妙地应用数学知识,会非常奏效。
“五步教学法”不仅激发了学生的学习兴趣,而且提升了学生学好数学的信心。学生的数学思维得到发展,综合运用知识与经验的能力获得提升,取得了较好的效果。我任教的两届毕业班,大部分学生都对数学学习建立起浓厚的兴趣,他们乐于钻研难题,敢于尝试新思路解题,学习能力有效提升。
(责编 吴美玲)
