双图交织 信息丰富

张永华

我们已经学习过扇形统计图、条形统计图、折线统计图、频数分布直方图，它们各自的特征是：扇形统计图利用扇形和圆来形象地显示部分与总体之间的关系：条形统计图利用等宽的条形的高来清楚地表示每个项目的具体数量：折线统计图利用折线既能表示出各个项目的具体数量.又能反映其变化情况：频数分布直方图利用长方形的面积大小来直观形象地反映数据落入某范围可能性的大小.中考命题者常常围绕着这些统计图，巧妙组合，设计出了许多题材新颖、双图交织、信息丰富、难度适中的统计试题，来考查考生的读图、析图以及由图中的信息进行推理预测的能力，要求较高.解决这类问题，要注意抓住两个统计图之间的对应关系，从中获取有用的信息，并做出恰当选择、合理判断.

例1 （2019年绍兴）小明、小聪参加了100米跑的5期集训，每期集训结束时进行测试，根据他们的集训时间、测试成绩绘制成如图1、图2所示的两个统计图，

根据图中信息，解答下列问题.

（1）这5期的集训共有多少天？小聪5次测试的平均成绩是多少？

（2）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，说说你的想法.

分析：（1）根据图1中的信息可以求得这5期的集训共有多少天，根据图2中的信息可以求得小聪5次测试的平均成绩.（2）根据题意，结合已知两个统计图中的信息及体育运动的实际，从训练时间与训练成绩的关系，说明自己的观点即可，本题答案不唯一，只要合理即可.

解：（1）这5期的集训共有5+7+10+14+20=56（天），小聪5次测试的平均成绩是（11.88+11.76+11.61+11.53+11.62）÷5=11.68（秒）.

（2）从集训时间看：集训时间不是越多越好，集训时间过长，可能会造成劳累，导致成绩下降，如图2中第5期与前面两期相比.

从测试成绩看：两人的最好成绩在第3期或第4期出现，建议集训的时间定为10—14天.

点评：本题考查了条形统计图、折线统计图等知识，弄清两个图中的数据及其关联是解题的关键，

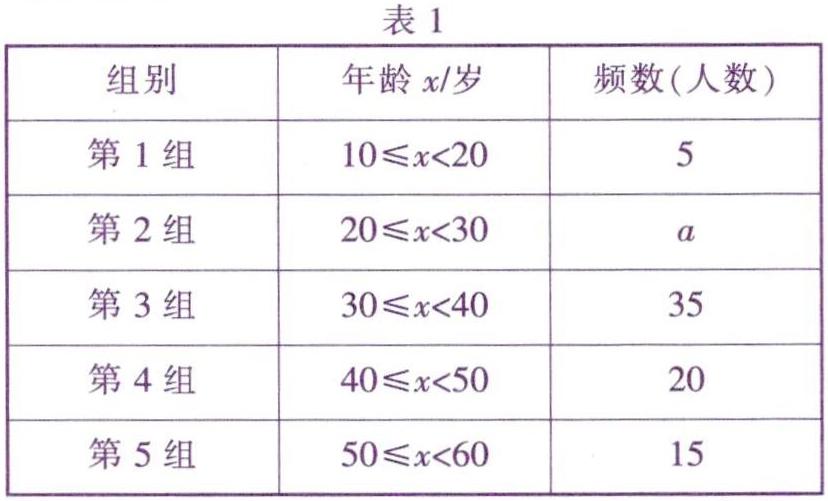
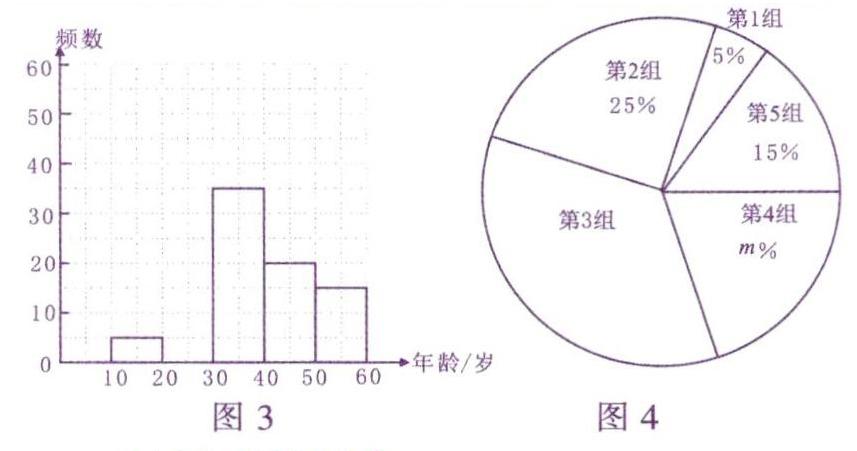
例2（2019年淄博）文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年3月“亚洲文明对话大会”在北京成功举办，引起了世界人民的极大关注.某市一研究机构为了解10—60岁年龄段市民对本次大会的关注程度，随机选取了100位年龄在该范围内的市民进行了调查，并根据收集到的数据制成了尚不完整的频数分布表（如表1）、频数分布直方图（图3）和扇形统计图（图4）.

（1）请直接写出a=____，m=____，“第3组”在扇形统计图中所对应扇形的圆心角大小是.

（2）请补全上面的频数分布直方图.

（3）假设该市现有10～60岁的市民300万人，岁数在40≤sx<50范围内的关注本次大会的人数约有多少？

分析：（1）根據题意和频数分布表中的数据，可以求得a，m的值和“第3组”在扇形统计图中所对应扇形的圆心角的大小.（2）根据（1）中a的值，可以将频数分布直方图补充完整.（3）根据样本估计总体的思想，利用频数分布表中的数据算出样本中岁数在40≤x<50范围内关注本次大会的人数的百分比为20%，即可估算出该市10—60岁的300万市民中岁数在40≤x<50范围内的关注本次大会的人数有多少，

解：（1）a=100-5 -35 -20-15 =25，m%=（ 20÷100） x100%=20%，“第3组”在扇形统计图中所对应扇形的圆心角是360°x 35/100=

1260.

（2）由（1）可知，岁数在20 ≤x<30范围内的有25人，由此可以补全频数分布直方图如图5所示.

（3）300×（20÷100） =60（万人）.

点评：本题考查频数分布表、频数分布直方图、扇形统计图、用样本估计总体等知识.解题的关键是明确题意，利用数形结合思想进行思考，

由两个统计图组合的双统计图问题常常将许多条件隐含在不同的统计图中，这就需要我们读图时，一定要结合两个统计图，进行双向联系，从图形中分析出有用的信息，获取相关的数据，找到解题的突破口，然后给出规范的解答过程.

练一练

根据图6、图7.回答下列问题.

去年该超市10月份的水果销售额11月份的水果销售额.（请从“>”“=”“<”中选一个填空）

参考答案：>