The nonlinear response of Cattaneo-type thermal loading of a laser pulse on a medium using the generalized thermoelastic model

Frshd Shkeriski, Mrym Ghodrt

aDepartment of Mechanical Engineering, Shahid Bahonar University of Kerman, Kerman, Iran

bSchool of Engineering and Information Technology, University of New South Wales Canberra, Canberra 2610 ACT, Australia

Keywords:Thermal wave propagation Nonlinear generalized thermoelasticity Cattaneo's heat conduction Laser pulse heating

ABSTRACT The nonlinear thermoelastic responses of an elastic medium exposed to laser generated shortpulse heating are investigated in this article. The thermal wave propagation of generalized thermoelastic medium under the impact of thermal loading with energy dissipation is the focus of this research. To model the thermal boundary condition (in the form of thermal conduction),generalized Cattaneo model (GCM) is employed. In the reference configuration, a nonlinear coupled Lord-Shulman-type generalized thermoelasticity formulation using finite strain theory(FST) is developed and the temperature dependency of the thermal conductivity is considered to derive the equations. In order to solve the time-dependent and nonlinear equations, Newmark's numerical time integration technique and an updated finite element algorithm is applied and to ensure achieving accurate continuity of the results, the Hermitian elements are used instead of Lagrangian's. The numerical responses for different factors such as input heat flux and nonlinear terms are expressed graphically and their impacts on the system's reaction are discussed in detail.The results of the study are presented for Green-Lindsay model and the findings are compared with Lord-Shulman model especially with regards to heat wave propagation. It is shown that the nature of the laser's thermal shock and its geometry are particularly determinative in the final stage of deformation. The research also concluded that employing FST leads to achieving more accuracy in terms of elastic deformations; however, the thermally nonlinear analysis does not change the results markedly. For this reason, the nonlinear theory of deformation is required in laser related reviews, while it is reasonable to ignore the temperature changes compared to the reference temperature in deriving governing equations.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Generally, for most engineering applications, using the Fourier law for heat conduction model is sufficient; nonetheless, the Fourier law cannot reflect appropriate temperature estimation at ultrafast heating. As a result, different non-Fourier models were proposed to reduce the deficiencies related to this problem for calculating the temperature [1]. The incidence of heat wave stream named second sound was initially proposed by Maxwell when presenting a modification of Fourier's law [2]. NonFourier heat flux model (Cattaneo's heat conduction model) to analyze heat transfer and stream between two rotating disc at different velocities was used by Shamshuddin et al. [3]. Based on their results, the rate of heat transfer decreased with higher non-Fourier effect due to the delay in thermal diffusion. The role of Cattaneo's heat conduction model in spinning axisymmetric stream of Maxwell fluid between coaxially spiraling discs was analyzed by Ahmed et al. [4]. Based on their findings, the temperature is reduced with the thermal relaxation time. Furthermore, a reduction in the concentration of the fluid happens with growing the parameters of homogeneous-heterogeneous reactions. Lord and Shulman [5] proposed a modified model of Fourier's law by defining a relaxation time. They managed to estimate finite speed of propagation to heat field. Othman and Mondal [6] applied the Lord-Shulman model to investigate thermoelastic rotating medium. They reported that the time-delay in Lord-Shulman model has a significant impact on the physical variables. Green and Lindsay [7] developed the second generalization theory that includes temperature as a dependent factor with respect to consecutive variables including two constants acting as relation times. Based on the results of Sarkar et al. [8]that employed two-temperature generalized thermoelasticity,new categorization for materials might be created where the time-delay factor be a new indicator of its capability to conduct heat in the system. In thermoelasticity, Green and Naghdi [9] expressed the next theory without any energy dissipation. In their model, a heat flux-temperature displacement gradient relation was substituted to Fourier's law. This resulted in developing a heat conduction correlation without the parameter of temperature rate and subsequently disclosed undamped thermoelastic waves. Green-Naghdi model to analyze the thermoelastic diffusion of the system was used by Zenkour [10]. The author also presented a new two-phase-lag model and claimed that there is an acceptable agreement between the results of this example and Green-Naghdi model. Biswas et al. [11] made a comparison between thermal analysis of magneto-thermoelastic medium using Lord-Shulman model and three-phase-lag model. Their results showed that the Lord-Shulman model indicates the maximum thermoelastic deformation. They also determined that the three-phase-lags model shows the least final deformation.Nikolarakis and Theotokoglou [12] used Lord-Shulman hypothesis to formulate generalized linear thermoelasticity equations of functionally graded materials (FGM). They discussed different values of volume fraction and its impacts on thermal response of system. To analyze the impact of higher-order time derivative on the variables, Abouelregal [13] presented a new model. The Taylor series expansions of the Fourier's heat were considered by the author. Based on their results, the higher-order time derivative order factor had an important impact on the final responses, resulting in a weakness in the impact of thermal propagation. An analytical technique for analyzing thermoelastic interactions in an infinite surface exposed to thermal shocks was presented by Youssef [14] who employed a direct way in Laplace transforms domain. The author derived the formulation based on state space approach and solved a boundary value problem of thermoelastic interactions by using Green-Naghdi theory. Most recently Kian and Attar [15, 16] conducted a series of investigations on thermoelasticity without energy dissipation theory and concluded that when thermal shock or/and relaxation time is higher, thermal nonlinearities appears rigorously.Their results showed that non-classical model without energy justified the fact that mechanical and thermal effects does not reach infinity instantaneously In order to analyze the generalized thermoelasticity behaviors of solids, Ieşan [17] employed Green-Naghdi model. The author investigated the thermal waves generated in an isotropic solid with the bounded region.Based on the results, unlike the classical model, the thermal waves at finite speed have any dissipative term. Various boundary conditions were considered by Erashlan [18] to present a good solution for inhomogeneous heat-generating tubes. Based on their analysis on plastic deformation, authors concluded that plastic deformation starts at the internal surface of the tube. Additionally, they found that plastic deformation starts from the inner surface that has the lowest temperature. Kundu and Dewanjee offered a new non-Fourier technique for thermal response of layers and applied Laplace Transformation method to analyze the problem [19]. Based on their findings, at tissue surface, the harmonic input heat flux intensifies non-Fourier behaviors. The impacts of temperature-dependent thermal conductivity on thermoelastic interactions in a medium was analyzed by Kumar et al. [20] using two-temperature Green-Naghdi model. They asserted that considering two-temperature theory may be determinative in finding temperature distribution. Shariyat et al. [21]analyzed the hydrothermoelasticity behaviors of hollow spheres exposed to mechanical and thermal shocks by using Lord-Shulman theory and considered the impacts of moisture absorption in the equations. Based on their results, the speed of wave propagation was reduced by considering the moisture impact.Shariyat et al. [22] expressed the significant impacts of moisture on the distributions of stress and stability of the medium by employing finite element method (FEM). The generalized thermoelasticity equations were solved by Abouelregal [23] who employed Laplace transform technique and concluded that the higher-order time derivative order terms had a considerable impact on the thermoelastic behaviors. It leads to weaken the impacts of thermal wave. Gunghas et al. [24] analyzed the distributions of stress, temperature and displacement in a no uniform,isotropic solid using Green-Naghdi theory. Based on their findings, no uniformity caused a reduction in temperature magnitude.

Most recently, many researches [25-30] carried out to investigate the laser pulse heating procedure based on hyperbolic or parabolic heat conduction correlation. The authors analyzed thermal propagation produced by laser radiation in different geometry. Employing Caputo fractional derivative, Mondal et al.[31] analyzed the transient phenomena in a stress free isothermal half-space using Lord-Shulman model of thermoelasticity and a non-Gussion pulsed laser type as the heat source. The authors observed a considerable variations in the physical quantities for various models due to using a laser pulse as a heat source. Al-Qahtani and Datta [32] proposed a semi-analytic finite element method for two-dimensional problem of an infinite thermoelastic sheet heated by laser pulse. The authors presented a quantitative model for laser producing ultrasonic wave within an anisotropic sheet. Lotfy and Gabr [33] analyzed a 2D deformations model for two-temperature model at a free semi-infinite sheet which is influenced under the thermoelastic wave resulted from pulsed laser. They discussed the effects of coupling parameters as well as thermal relaxation times on system's response. Othman [34] using Lord-Shulman theory studied the responses of micropolar thermoelasticity Based on their results the considered time parameter has a remarkable influence on all responses. Verses et al. [35] analyzed the laser production of ultra sound induced-coupled thermoelasticity. For solving the equations, the authors employed numerical solutions based on finite difference method (FDM) and showed that the impacts of coupling terms on the wave propagation and speed. Several numerical techniques such as FEM were developed by some researchers such as. The impact of heat transfer in metals on the factors of thermal stresses resulted from pulsed laser impact was analyzed by Zimin et al. [36]. The authors considered the thermoelasticity dynamic problem as two-stage procedure. The first step is determining the time of radiation pulse action; the second step relies on heat transfer process dynamic following the end of laser pulse action. Based on their results, the structural changes have significant impacts on the considered parameters.

A detailed survey of the existing literature reveals how thermal response of a structure due to a laser pulse still requires further study. This study aims to analyze the nonlinear thermal wave propagation of a homogenous thermoelastic finite length surface exposed to thermal loading provided by laser pulse based on Lord-Shulman and Green-Lindsay theories. Additionally, the impacts of laser pulse nature, as well as nonlinearity of governing equations on system's response are analyzed in detail.

In this research, the nonlinear thermal and mechanical wave propagation in a medium under the impact of laser pulse(shown in Fig. 1) are investigated. The top face of the medium is exposed to the laser pulse and the bottom face is subjected to heat convection with the environment. The considered quantities are functions of coordinaterand time given that the changes can be ignored in two other coordinates.

For entering a finite velocity of heat generation, a modified model presented by Lord-Shulman is employed in order to represent the coupled nonlinear equation of heat conduction and motion for material points [37-39]:

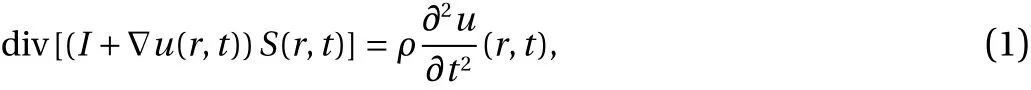
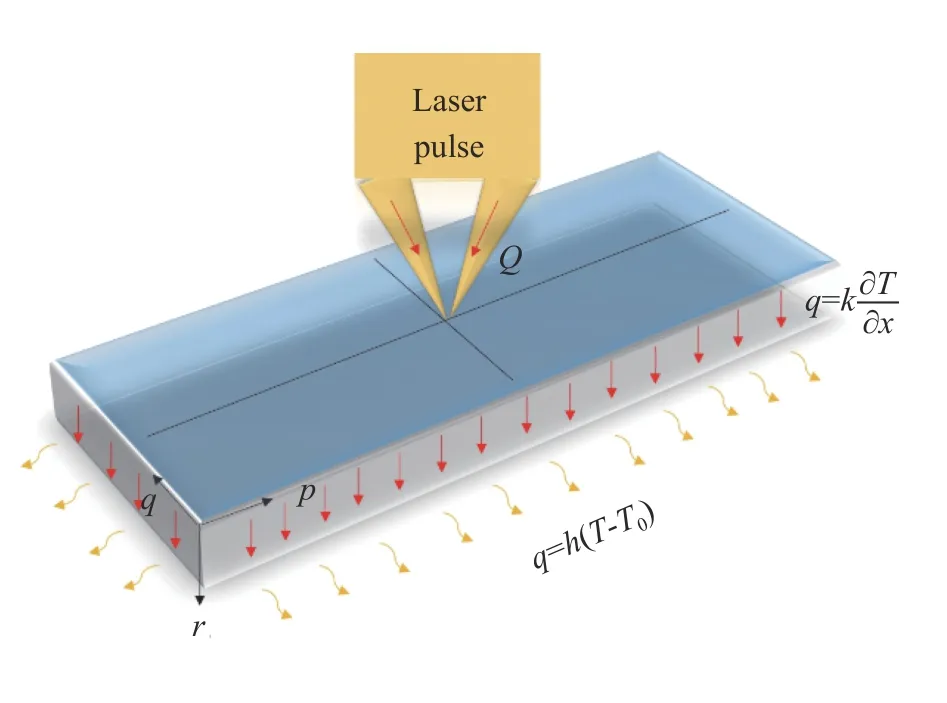
Fig. 1. Geometry and coordinates

The nonlinear strain equation is considered as [40, 41]:

Finally the nonlinear equations of motion and energy are expressed as:

As mentioned, in this research, the thermal conductivity is considered as variable and introduced as a nonlinear function of temperature [42]:

As shown in the Fig. 1, the top surface of the medium is subjected to laser-pulse and its thermal boundary condition is expressed by employing generalized thermoelastic analysis based on the heat conduction law of generalized Cattaneo model(GCM). The other face experiences convection with the ambient temperature, and it is unchanged. All particles are considered in a steady state initially.

The medium surface is influenced by laser pulse given by the heat input:

The Gaussian distribution of the heat flux in terms of the absorbed laser power (Q0) and laser beam radius (a) is specified as[43-46]:

The temporal profile of laser pulses is expressed by an exponential function

In order to find an acceptable solution for the obtained coupled nonlinear equations (Eqs. (4) and (6)), in this study,FEM is employed, due to its capability in solving nonlinear and coupled problems [42]. Based on the considered finite strain theory (FST) methodology and nonlinear thermal analysis (considering the temperature changes compared to the reference temperature), a set of complex couple equations are resulted. To obtain numerical solution, Galerkin finite element procedure is applied. A good iterative algorithm is added to the numerical solution procedure due to different nonlinear parameters in the equations (which is presented in detail in the following sections). In numerical method, the best accuracy is obtained when the shape function order is considered greater than that of the weak form of the equations [47]. For this purpose, nonlinear Hermitian elements are applied to eliminate possible errors occurs in the finite process using the first-order elements. To achieve more accurate solution, the shape functions with larger order than the weak form's order is considered. For this reason,the temperature and the displacement in Eqs. (4) and (6) are followed by nonlinear shape functions of Eq (12):

In these equations,nis the number of elements. The nodal vectors of temperature and displacement arerespectively.The nonlinear shape functions are expressed by

Equation (13) shows the nonlinear Hermitian shape functions used in this research (lis the length of the medium).

One of the main section of FEM procedure is to reduce the order of derivations using the weight function of (w) for employing thermal boundary conditions appropriately. By doing so, the final form of the FEM equations are obtained as follows:

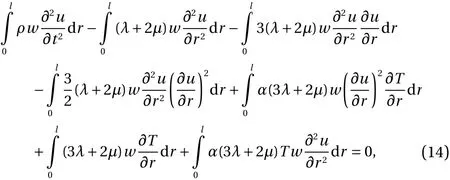
Compared to the previous study [15, 28, 30], the nonlinear terms below are added to present equation and up to third derivative terms are considered in this research:

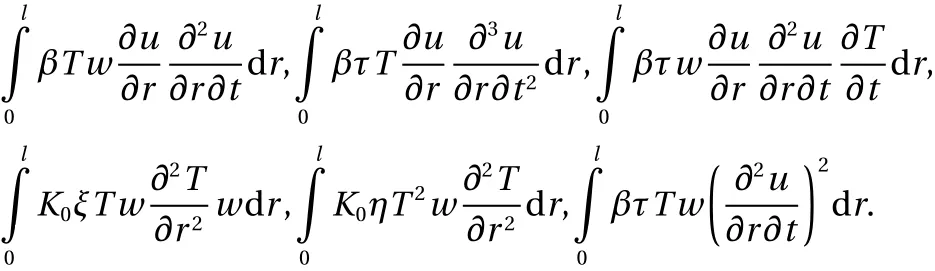
Hence, the Galerkin's form of Eqs. (4) and (6) is presented as follows:

This part of the study presents a solution for the nonlinear system of ordinary finite element equations. To find a direct response for the governing second-order differential equations without their transforming to a first-order system, Newmark method is employed [52, 53]. The principal property of this solution process is the discretization of time domain to time steps. In the present equations, time is expressed in the form of time step and n is the number of time increment [49]:

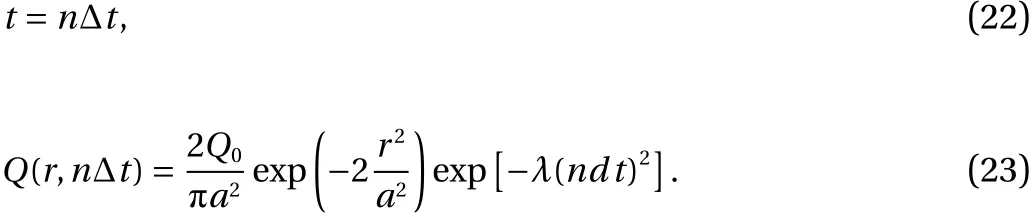
By employing the time integration and the second-order Runge-Kutta, the following algorithm is introduced, and the final form of previous matrices are expressed as Eq. (25) [54]:

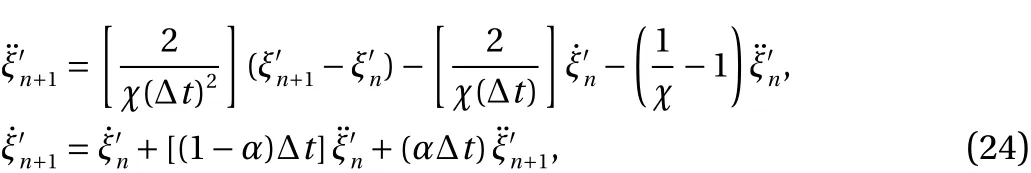
where χ and α are the terms controlling the stability of NewMark technique that considered 0.5. For the first time step,andas the initial conditions are considered to be 0. The acceleration vector is calculated as:

The assembled matrix is nonlinear because the matrixes of element stiffness are asymmetric and nonlinear. The assembled nonlinear equation might be solved by performing boundary conditions and applying an iterative technique. The iteration technique Picard is employed in this study:

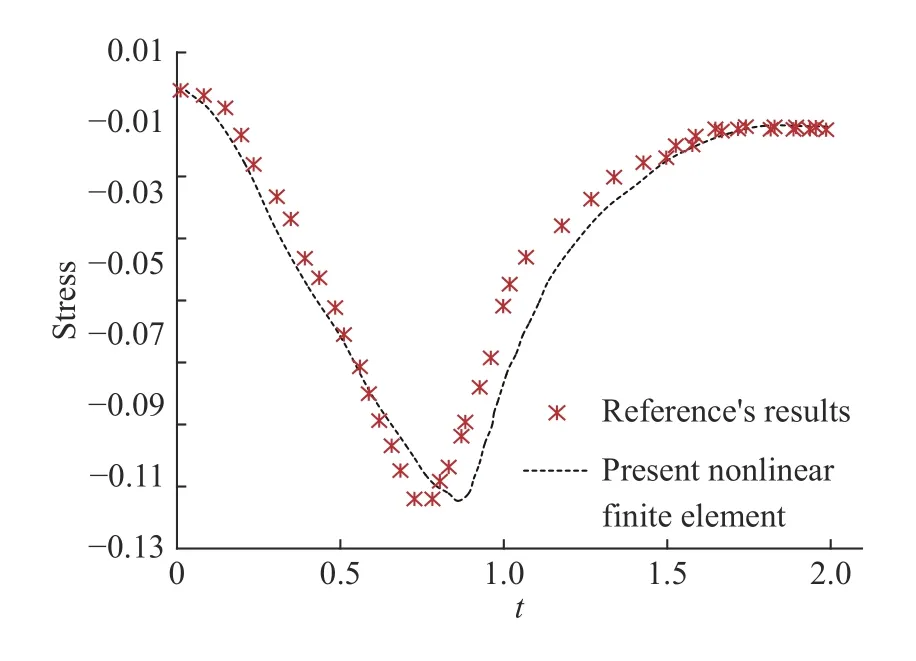
Fig. 2. A comparison between stress variations in a half-space subjected to thermal shock (x=0.1)

Fig. 3. A comparison between temperature variations in a halfspace subjected to thermal shock (x=0.1)

Table 1 Material properties of steel and geometric parameters [56]

A comparison is conducted between the obtained results from this study and that of Ting and Chen [55]. The comparison proposed a solution for an isotropic half-space under a convection heat transfer. The boundary conditions are expressed as:

In order to compare the results, ξ ,η are considered to be zero. A copper medium is chosen with these properties:

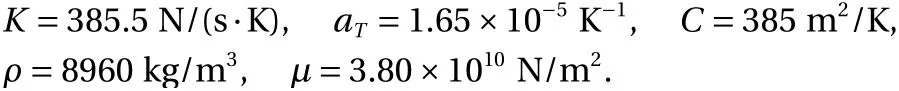
Finally, a reasonable agreement is seen in this comparison which is shown in Figs. 2 and 3.

Fig. 4. Temperature distribution obtained by Lord-Shulman model versus time,τ0=0.01,t=nΔt,b=λ=10×Δt

As can be seen from Fig. 2, the applied temperature variation in the boundary points leads to a stress wave in the medium.Based on Fig. 3, the temperature distributions of the medium increase by time and the temperature converges toward a specific value, as time tends to infinity. The observed trend can be explained by the fact that the first points of the body exposed to the temperature change while the end points of the medium are subjected to ambient convection heat transfer. Hence, the final temperature of the medium gradually tends to a certain value. It is worth noting that the reference results were obtained using linear shape functions whereas in the present research the nonlinear Hermitian elements are applied. Also, the linear strain function was considered in the reference study. This can be the prime reason for the minor difference observed in the comparison.

The results of studying the wave propagation phenomenon in the medium under the influence of laser heat flux are discussed. In the first part, the results are presented by applying Lord-Shulman theory to express the governing thermoelasticity relations. Subsequently, the results of the Green-Lindsay model are presented and compared with the results of the Lord-Shulman Hypothesis. The elements' size is accurate enough that no additional calculations are required. In other word, the results do not change by further reducing of the size of the considered elements. Table 1 presents the required parameters in Eqs. (4)and (6). These parameters include material properties, geometrical parameters, and parameters related to the laser flux and geometry.

Figure 4 demonstrates the time variation of temperature for various points of the body. In numerical time integration process, short time discretization is considered to have more observable reflection of wave propagation. It can be seen from the results that the points in contact with the heat flux experience higher temperature variations.

Based on the laser flux equation (Eq. (11)), it is evident that the applied flux has its highest value at early times and reaches to zero over time. This phenomenon is well illustrated in the results of Fig. 4. It is also clear that the resulting thermal wave is moving along the length of the body over time. As can be seen from Fig. 4, the direction of the arrow illustrates the maximum point of change in temperature at different time which moves progress through an outlined set of time.

Fig. 5. Thermal stress wave propagation obtained by Lord-Shulman model versus time,τ0=0.01,t=nΔt,b=λ=10×Δt

Figure 5 demonstrates the thermal stress distribution resulted by the laser input flux. Based on the findings, the applied flux initiates the stress wave in the medium that moves along the length over time. The numerical results also indicates that the amplitude of the wave decreases with time. This is due to decreased input laser flux over time. Based on the findings in Fig. 5,the applied flux initiates a tensile stress wave. In fact, given the input flux and boundary conditions, the medium initially experiences an expansion and eventually, tensile stress reaches to the endpoints and then the inverse wave (pressure wave) begins to propagate in the body.

The displacement variation of the points affected by the applied flux are also plotted in Fig. 6. The results illustrate that the displacement wave transfers over time. Regarding the applied flux, the starting points (points closer to the laser flux) have the maximum displacement variations. The amplitude of the passing wave decreases as the energy received from the source decreases over time.

In order to gain better understanding of the wave propagation phenomenon, the displacement, distribution along the r direction is plotted in Fig. 7. As can be seen from this figure, the applied flux acts as a shock and makes significant changes in the location of the first points (closer to the boundaryx= 0) compared to the end points of the body. That means the first points on the body experience more heat flux, comparing to the end points which are under the impact of heat convection with the environment.

Figure 8 shows the variation in temperature and stress distribution against time and location, respectively. As can be seen from this figure, the first points (closer to the boundaryx=0) of the medium experience higher temperature variations, and as for the laser input flux profile, this temperature decreases by time. Also, as the end points of the body are affected by the heat transfer of the environment, this variation decreases along the length of the body, which is evident in the results of both Figs. 4 and 8.

In the present research, both nonlinearity of strain and temperature are deemed to derive the governing equations. Figure 9 shows a comparison between the nonlinear results obtained in this research and the linear response obtained by eliminating the nonlinear terms. It can be seen from Fig. 9a-9c that the nonlinear terms in the formulations have increased the system's flexibility. Hence, the terms related to the large deformations indicate substantial impact on the displacement and stress distribution of the system.

Figure 9d is associated with the medium temperature variations compared to the reference temperature. As can be seen from this figure, the nonlinear terms related to the temperature have no effect on the obtained results from the solution of system's governing equations (Eqs. (4) and (6)). Consequently, it is reasonable to employ the assumption of ( (T-T0)/T0＜＜1) to somewhat simplify these equations.

Figure 10 shows the effects of input parameters associated with the laser geometry and the heat flux specified by β0. Based on the results presented in Fig. 10a, the final response of the system is highly affected by the laser geometry and its heat flux.

Figure 10b shows the propagation of the stress wave along the length of the medium in the transient mode from tensile to compressive. The stress wave is converted from tensile to compressive in the period of 1 8 ＜n＜40 that was also evident in Fig.5. In addition, the stress wave is influenced by the ratio of heat flux per laser's radius β0=2Q0/(πa2).

As stated, in the following, the results for Green-Lindsay model of generalized thermoelasticity is presented. Based on the Green-Lindsay model [57-59] and Green-Lagrange strain tensor,the stress can be rewritten in Eq. (29) as below:

Fig. 9. Comparison between system's response predicted by linear and nonlinear thermoelasticity equations

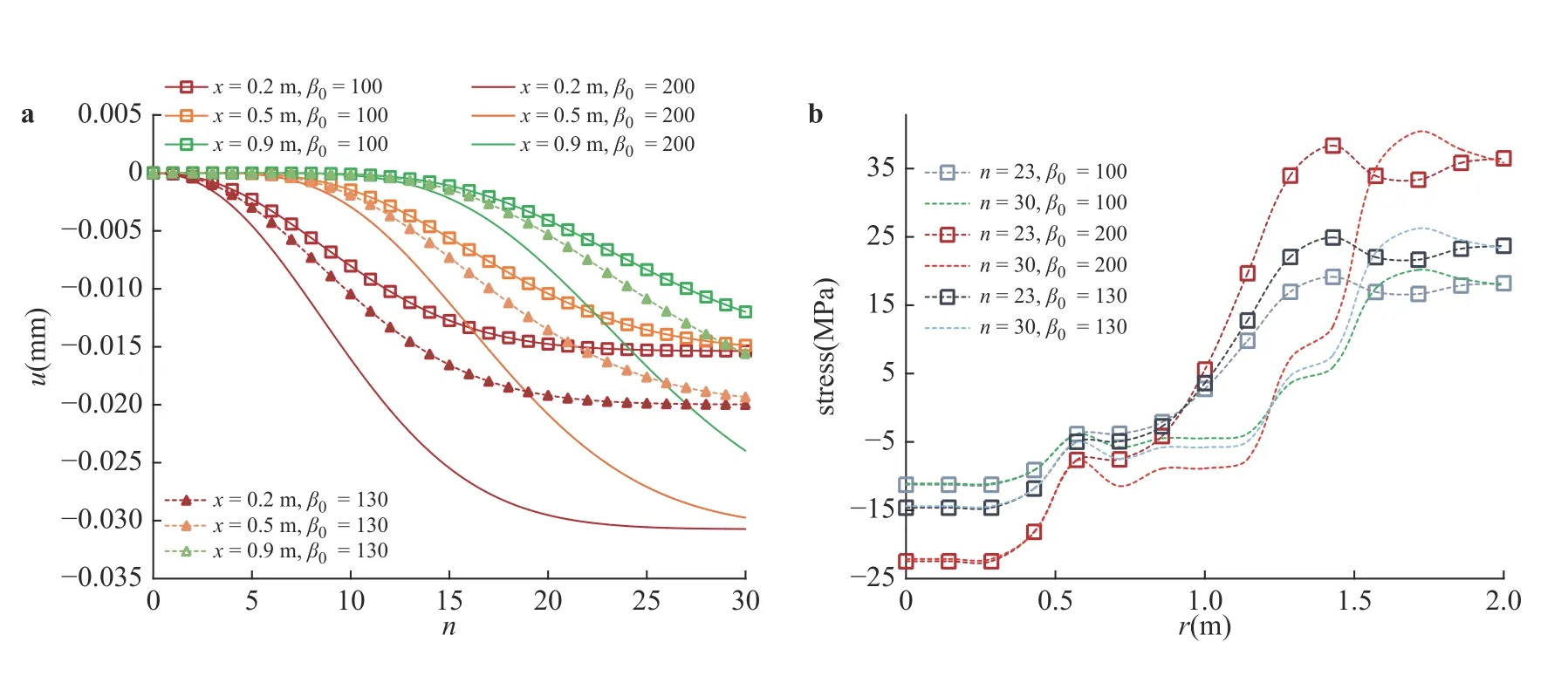
Fig. 10. Displacement and stress wave propagation by Lord-Shulman model versus r

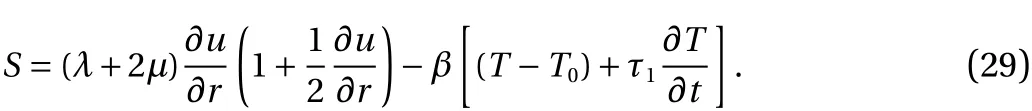
By substituting the stress equation (Eq. (29)) into the coupled equations of momentum and energy (Eqs. (1) and (2)), the relevant equations are rewritten. Finally, multiplying the weight function and integrating over the specified interval, the elements of mass, stiffness, and damping matrix are obtained:

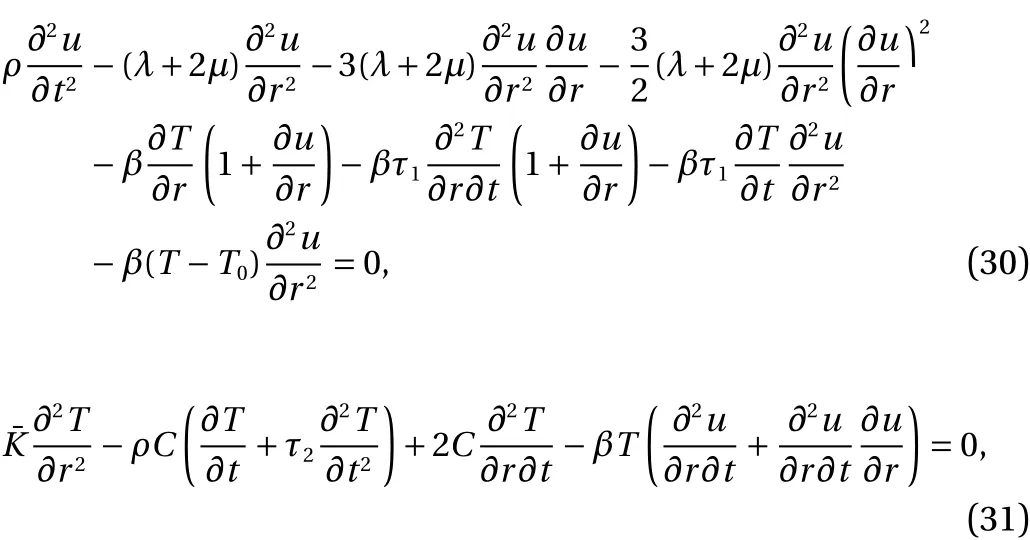
Fig. 11.Displacement distribution versus time in Green-Lindsay generalized thermoelasticy model τ 1=0.01,τ2=0.01,

The results of displacement and temperature for the defined boundary conditions in Eq. (8) (the medium is exposed to the laser heat flux) are shown in Figs. 11-13. As can be seen from these figures, there is a significant difference between displacement distribution in Green-Lindsay model and Lord-Shulman model. It can be inferred that the displacement is damped in Green-Lindsay model quicker than in Lord-Shulman Model,due to the lag time τ in the stress relation which is considered in Green-Lindsay model.

Figures 11 and 12 show the displacement wave distribution in the body. As can be seen from these figures, the first points of the body (closer to the boundaryx=0) have the maximum displacement that moves throughout the body by time (due to the movement of the wave along the length of the body). As evident,the wave propagation is fairly visible when comparing the maximum displacements of the medium atn= 2 andn=14 (nis the number of time increment). The results also demonstrate that in comparison with the Lord-Shulman model, the displacements of the first points in Green-Lindsay model lean towards zero over time due to the lag time considered at the stress equations in Green-Lindsay model.

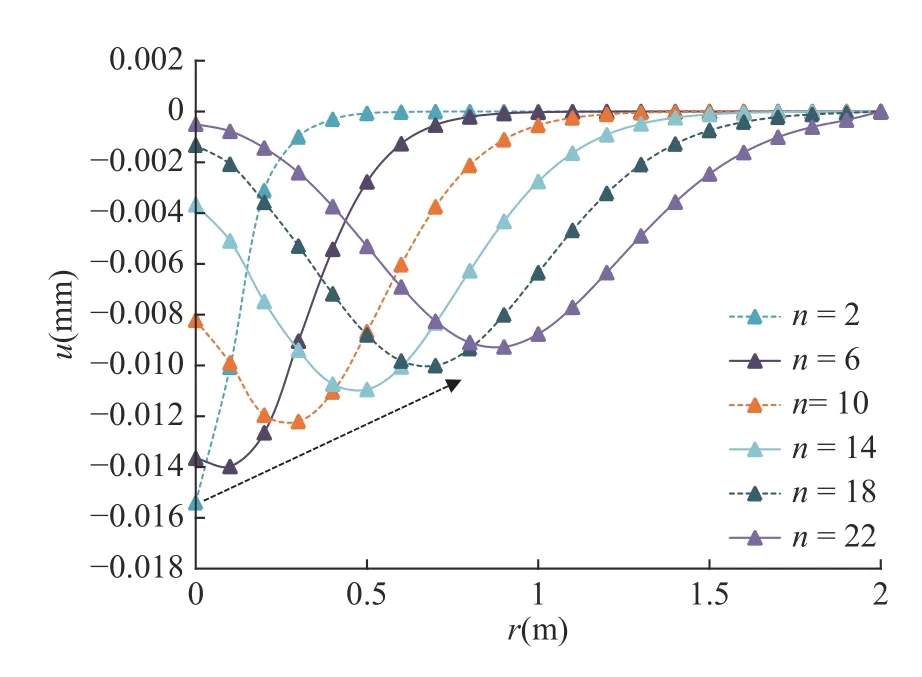
Fig. 12. Displacement distribution versus r in Green-Lindsay generalized thermoelasticy model.

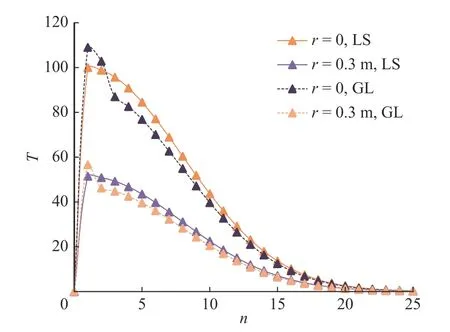
Fig. 13. Comparison between the obtained temperature distributions in two different generalized thermoelasticy models.

Figure 13 compares the temperature variation obtained by Green-Lindsay and Lord-Shulman theories. The results show that the aforementioned hypothesis provides approximately same temperature in nonlinear thermal analysis of laser shock with applied boundary conditions (Eq. (8)).

In this research, the laser pulse heating of a solid surface was studied using a Hermitian finite-element process. The coupled governing equations were derived based on nonlinear Lord-Shulman generalized thermoelasticy and FST. The nonlinear temperature-dependency of thermal conductivity coefficient is considered and the thermal boundary condition was applied according to GCM. The thermoelastic wave propagation in a medium under the thermal shock was investigated and the obtained results were compared with the results of Green-Lindsay model.

Some of the innovations of this study can be summarized as follows:

● Using FST, the nonlinear form of the strain equation in terms of the displacement component was employed to derive the nonlinear coupled equation of Lord-Shulman model for generalized thermoelasticity.

● Temperature variations in the general form of equation was employed to achieve more accuracy

● The nonlinear Hermitian elements were considered to present precise nonlinear finite element solution.

● The impacts of non-linear terms related to the temperature variation and large deformations were explored.

● The study results are summarized below.

● The final deformations in the medium strongly depends on the nature of the laser's thermal shock and its geometry such as beam radius.

● The nonlinear terms related to the large deformations have foremost influence on the final deformation; so, to obtain more accurate analysis of laser, large deformation is recommended.

● The nonlinear thermal analysis related to temperature variations does not result in a notable impact on the responses;hence, using lower temperature changes to simplify the solution is a reasonable assumption

● Comparing the results of Lord-Shulman and Green-Lindsay model indicates that the elastic wave propagation in Green-Lindsay model is more visible than that of Lord-Shulman model which is due to the presence of lag time in the stress relation in Green-Lindsay model.

List of Nomenclature

aLaser beam radius

CSpecific heat parameter

hHeat convection parameter

KThermal conduction parameter

lThe length of elements

nThe number of time increment

P(r) Functional shape

QThermal flux

rLength dimension

SPiola stress

TTemperature

tTime

uDisplacement

Greek letters

αThermal expansion

ΔtTime increment

ρ Density

μShear parameter

λLame parameter

τ0relaxation time

τ1,τ2Green-Lindsay parameters

τ0Lord-Shulman parameter

εStrain

ξ,η Thermal conductivity related parameters