Nonlinear energy harvesting from vibratory disc-shaped piezoelectric laminates

Abdolrez Pshrvesh, Rez Moheimni, Hmid Dlir

aSchool of Mechanical Engineering, Purdue University, West Lafayette, IN 47907, USA

bDepartment of Mechanical and Energy Engineering, Purdue School of Engineering and Technology, Indianapolis, IN 46202, USA

Keywords:Nonlinear resonator Coupled electromechanical modeling Energy harvesting Piezoelectric laminate

ABSTRACT Implementing resonators with geometrical nonlinearities in vibrational energy harvesting systems leads to considerable enhancement of their operational bandwidths. This advantage of nonlinear devices in comparison to their linear counterparts is much more obvious especially at small-scale where transition to nonlinear regime of vibration occurs at moderately small amplitudes of the base excitation. In this paper the nonlinear behavior of a disc-shaped piezoelectric laminated harvester considering midplane-stretching effect is investigated. Extended Hamilton's principle is exploited to extract electromechanically coupled governing partial differential equations of the system. The equations are firstly order-reduced and then analytically solved implementing perturbation method of multiple scales. A nonlinear finite element method (FEM) simulation of the system is performed additionally for the purpose of verification which shows agreement with the analytical solution to a large extent. The frequency response of the output power at primary resonance of the harvester is calculated to investigate the effect of nonlinearity on the system performance. Effect of various parameters including mechanical quality factor, external load impedance and base excitation amplitude on the behavior of the system are studied. Findings indicate that in the nonlinear regime both output power and operational bandwidth of the harvester will be enhanced by increasing the mechanical quality factor which can be considered as a significant advantage in comparison to linear harvesters in which these two factors vary in opposite ways as quality factor is changed.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Development of novel low power electric devices thanks to the recent major progresses in both micro-electro-mechanical systems (MEMS) and microelectronics technologies has put forward the idea of environmental energy harvesting to provide smart devices with a lifetime reliable power supply. The superiority of energy harvesters in comparison to different types of batteries can be better highlighted in applications at which battery replacement is either an impossible or arduous process. Implantable medical devices (IMDs) [1] due to their inaccessibility and wireless sensor networks (WSNs) [2] due to their large number of nodes spreading over a large area are good examples of such systems.

The most important factors which must be addressed to select an environmental energy source as a candidate for energy harvesting are its availability and the efficiency of its conversion to electrical energy. Roundy et al. [3] showed that among various types of sources including thermal, kinetic, electromagnetic,solar, and wind energies, the kinetic one is the most promising candidate considering the mentioned two factors. To extract the kinetic energy content in vibratory motions, some multiphysics mechanism capable of coupling mechanical and electrical domains is needed. Kinetic energy harvesters mostly utilize electrostatic [4, 5], electromagnetic [6, 7], or piezoelectric [8, 9]mechanisms to accomplish the energy transduction.

Nonlinear energy harvesting realized by utilization of nonlinear electromechanical resonators has increasingly become the focus of the researchers’ interest lately. The main reason behind this fact lies in highly limited bandwidths of linear systems which restricts the linear harvester from deployment to real applications. In linear harvesters, the efficiency of the device can be enhanced by limiting the mechanical damping effects and increasing the quality factor of the system. That occurs while a slightly damped resonator due to existence of the sharp peak in its frequency response has a relatively narrow bandwidth [10-15].

It is supported by several researches that mono-stable nonlinear harvesters through the bending created in their frequency response curve are capable to circumvent the so-called “gainbandwidth dilemma” when subjected to a single-harmonic excitation [16-22]. Furthermore, based on experimental observations higher amount of energy may be extracted from randomly vibrating objects by using nonlinear bi-stable harvesters which arises from their noise-assisted jumps between different energy wells [23-25]. The nonlinear behavior of an energy harvester may arise due to the nonlinearity of electroelastic materials employed as an intermediate media in the process of energy conversion [26], or through the connection of the mechanical energy harvesting device to the nonlinear circuits of energy extraction and storage [27]. However, the geometric nonlinearity of the mechanical structure may be considered as the most significant source of nonlinearity in these devices [28]. The investigation of the effect of geometric nonlinearities due to midplane stretching, nonlinear curvature and nonlinear inertia in energy harvesting beams with doubly clamped [29] and cantilevered [30] configurations are among the previously accomplished researches in this field.

In this paper the nonlinear behavior of a piezoelectric harvester composed of a circular laminated plate is investigated. To accomplish this goal an electromechanically fully-coupled nonlinear model of the system considering nonlinearity due to midplane stretching is presented. Extended Hamilton’s principle is exploited to extract the governing equations of the proposed model. The perturbation method of multiple scales is utilized to analytically solve the derived equations. Thereafter, a nonlinear finite element method (FEM) simulation of the system considering the electromechanical coupling effect is performed to verify the analytical results. Subsequently, the behavior of the harvester and its capability in wideband energy harvesting is studied at primary resonance for different excitation levels, mechanical quality factors and connected electrical loads.

Figure 1 shows a schematic of the harvester which is constituted of a clamped circular laminated composite plate composed of a base layer of thickness 2hBenveloped by two piezoelectric layers each of thickness. The harvester is supposed to be excited by the harmonic oscillation of its clamped edge represented by. A concentrated proof massMis connected to the center of the plate for the sake of resonance frequency lowering. The base layer is supposed to be made of some conductive material serving also as a shared electrode for both piezoelectric layers. In addition two conductive circular electrodes with radiusare placed at the bottom and top sides of the plate. These electrodes are supposed to be thin enough so that their effect on the overall stiffness of the plate can be supposed as negligible.The piezoelectric layers are polarized along the thickness and in opposite directions. The generated voltages of the piezoelectric layers are added up by connecting top and bottom electrodes to the loadR.

To formulate the nonlinear behavior of the laminated plate the nonlinear plate theory which uses von Karman strains in conjunction with the classical linear theory based on Kirchhoff’s hypothesis, is used. Employing a cylindrical coordinate system centered on the reference plane of the plate and denotingr,θ andzcoordinates by 1, 2 and 3 respectively, the only nonzero components of strain in an axisymmetric circular plate will be:

wheree1ande2denote the strain components on the reference plane:

whereuandware displacement components of an observed reference point inrandzdirections respectively and the subscriptrrepresents their differentiation with respect to the radial position of the point.

Extended Hamilton’s principle can be stated as:

whereT, Π andWncrepresent the kinetic, potential and nonconservative energies.

The variation of the kinetic energy is:

Fig. 1. Schematic view of the disc-shaped harvester

Denoting the mass densities of the base layer and piezoelectric materials by ρBand ρP, the mass per unit aream(r) may be written as:

The potential energy stored in each layer can be written in the following general form:

where D is the electric displacement vector, c, h, and β denote stiffness, piezoelectric constant and inverse permittivity represented in Voigt notation. For the base layer one should substitute:

whereEandνdenote Young's modulus and Poisson’s ratio of its constitutive material. Therefore the variation of the total potential energy can be written as the following form:

Substituting Eq. (1) into Eq. (8), one obtains:

where

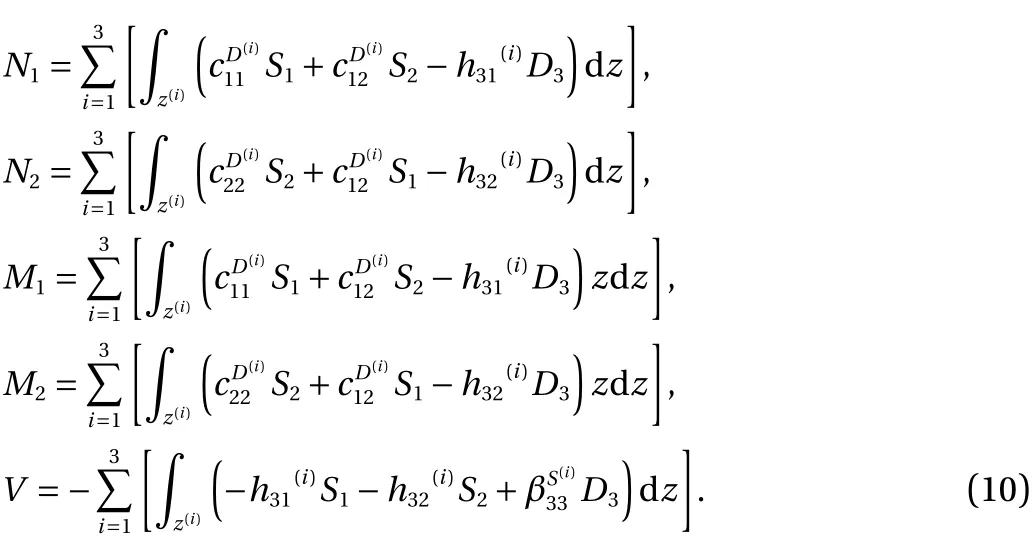
The variation of the nonconservative energy can be written as:

where the nonconservative force is the summation of inertia and damping forces:

wherecis the effective damping coefficient representing air or material damping.

According to Gauss’s law the surface charge density σ stored on the upper electrode is:

Substituting Eqs. (12) and (13) into Eq. (11), one obtains:

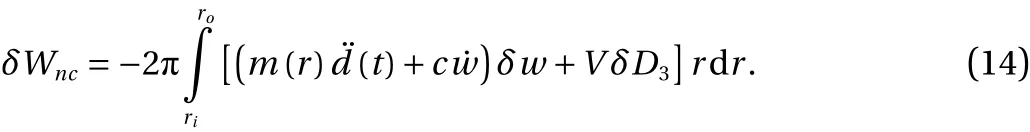
Finally by substitution of the derived energy variations into Eq. (3), the governing equations of the system are found as:

Also the boundary conditions are derived as:

Substituting Eq. (1) into Eq. (10) and calculating the integrals assuming the piezoelectric layers to be orthotropic and to have identical material properties denoted by cD, h, and β, one obtains:

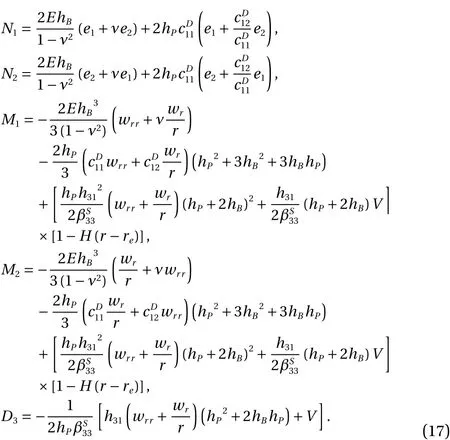
Neglecting the in-plane inertia, Eq. (15a) can be satisfied by introducing the stress function Φ (r,t) defined by:

Writinge1ande2as functions of force resultantsN1andN2from Eq. (17), substituting into Eq. (2) then eliminatinguandw,the following compatibility equation is derived:

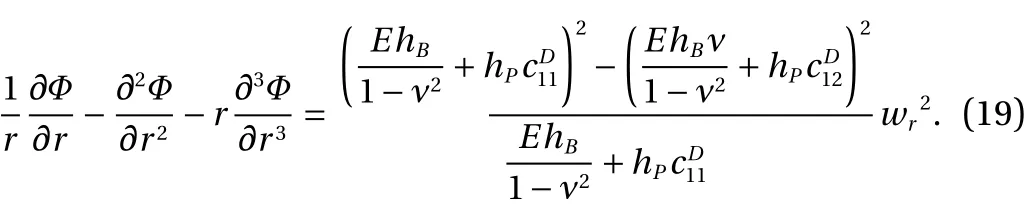
Also the boundary conditions on Φ (r,t) can be found by settingu=re2=0 at the clamped edge as:

Substituting Eqs. (17) and (18) into Eq. (15b) the differential equation of motion is found as:

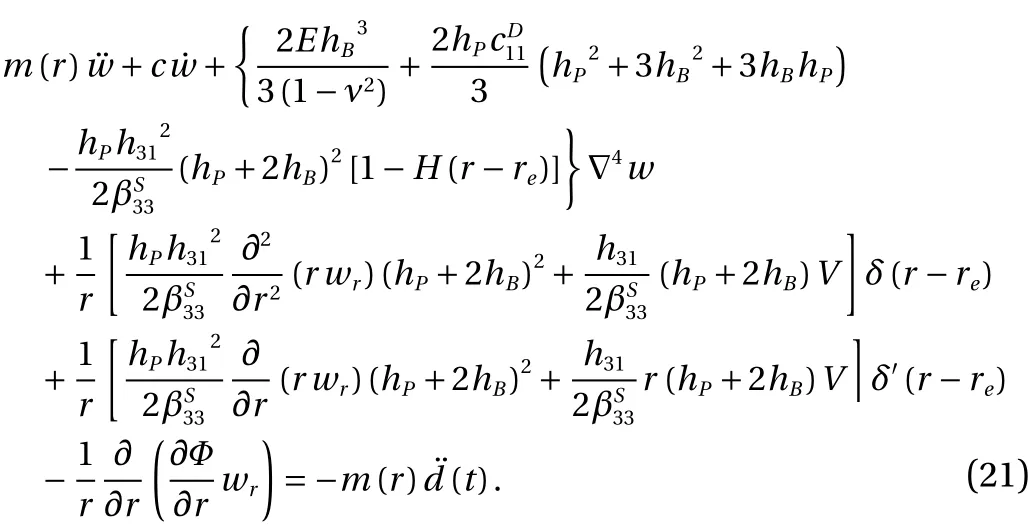
The Galerkin procedure can be used to reduce the above distributed parameter equation into a single nonlinear second-order ordinary differential equation. To this end using a one mode assumptionw(r,t) can be written as:

where φ (r) is the first mode shape of a clamped circular plate[31]:

whereJ0andI0respectively denote regular and modified Bessel functions of the first type.

Substituting Eq. (22) into Eq. (19), the solution of that equation can be written as:

Therefore ψ (r) should satisfy the following equation and boundary condition:

where

The following expansion can be used for ψ′:

By substitution of the above solution into the boundary condition of Eq. (26), the following equation for ξkis derived:

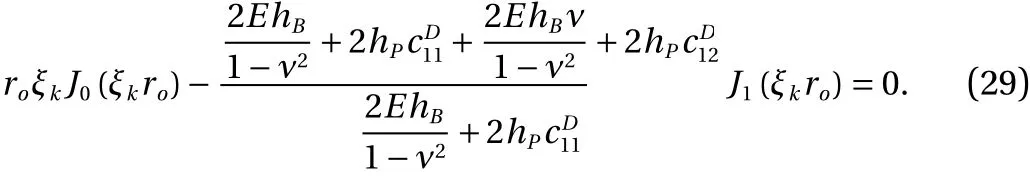
Substituting Eq. (28) into Eq. (25), multiplying byJ1(ξkr) then integrating the result with respect torfromr=0 tor=ro, results in:

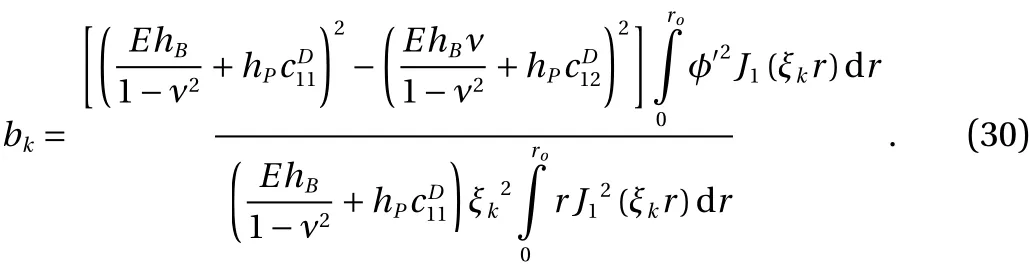
Substituting Eqs. (17), (18), (28) and (30) into Eq. (15b), multiplying the result by 2 πrφ(r) and integrating fromr=0 tor=ro,the ordinary differential equation of motion is found. Also calculating the charge density from Eq. (17), integrating it over the electrode area then using Ohm’s law leads to an equation governing the output voltage. Therefore the coupled electromechanical nonlinear equations of the harvester can be written as:

where base motion is supposed to be a single harmonic with excitation frequency Ω (= 2πfexc):

The solution of Eq. (31) may be derived by employing the perturbation method of multiple scales as:

where amplitudeaand phase γ are the solutions of the following set of equations:

where ωE= 2πfEin the above equation is the short-circuit (E=0)linear resonance frequency of the system:

The average output power of the harvester can be calculated by integrating the instantaneous power delivered to the external load:

Finally, substitutingVfrom Eq. (33) into the above equation,one obtains the following expression for the output power:

The maximum power will occur at the peak vibration amplitude:

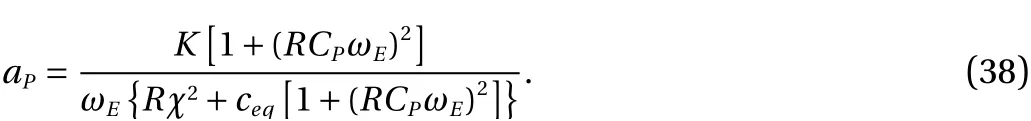
Also using the frequency response function in Eq. (34), the half power or 3db bandwidth of the harvester in the nonlinear regime is obtained as:ment necessitatesC1continuity for variablewtogether withC0continuity for variablesuandD3. Therefore a two-node ele-

To verify the above-described analytically calculated results,a numerical solution to the nonlinear problem employing the FEM is presented in this section. To this end firstly using the variational form given in Eq. (9), a structural element possessing both mechanical and electrical variables as degrees of freedom is developed. According to this equation, compatibility requirement requires four degrees of freedom at each node including radial displacement (u), transverse displacement (w), slope(∂w/∂r) and electric displacement along the thickness direction(D3). A schematic view of the element together with the degrees of freedom is shown in Fig. 2a. Actually, this element presents a thin-walled ring within the disk as shown in Fig. 2b and the value of the variables at each node refers to their value on the inner and outer surfaces of the ring.

The variables are interpolated within each element using Hermite polynomials as shape functions:

where q is the vector presenting the nodal values of the variables:

and H is the matrix containing the shape functions:

一是在指导思想上，必须长期坚持以人为本的原则，坚决抛弃 “重工程、轻移民，重搬迁、轻安置”的传统思维，把维护移民合法权益、保障移民长远发展放在更加突出的位置。二是在工作目标上，必须更加重视移民收入翻番、农业现代化和移民新农村建设，重视移民生活水平的全面提高。三是在工作重点上，必须加大工作力度，在深入推进城乡发展一体化、加快发展现代农业、着力促进移民增收、加强社会建设、建设移民美丽家园等方面工作取得新突破。四是在工作路径上，必须明确移民工作方向，找到破解移民工作难题的有效路径，坚持工业反哺农业、城市支持农村和多予少取放活方针，加大强农惠农富农政策力度，切实让广大移民共享现代化成果。

Substitutingu,wandD3from Eq. (40) into Eqs. (9) and (17),one obtains:

The mass matrix can be derived similarly by substitution of Eq. (40) into Eq. (4) as:

Finally substituting Eq. (40) into Eq. (14) the total virtual work done by the nonconservative forces can be written as:

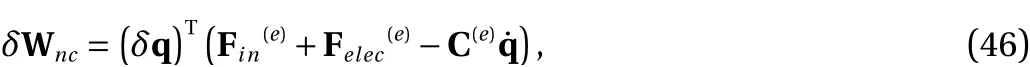
in which nodal inertial force vector, nodal electrical force vector and mechanical damping matrix are as follows:

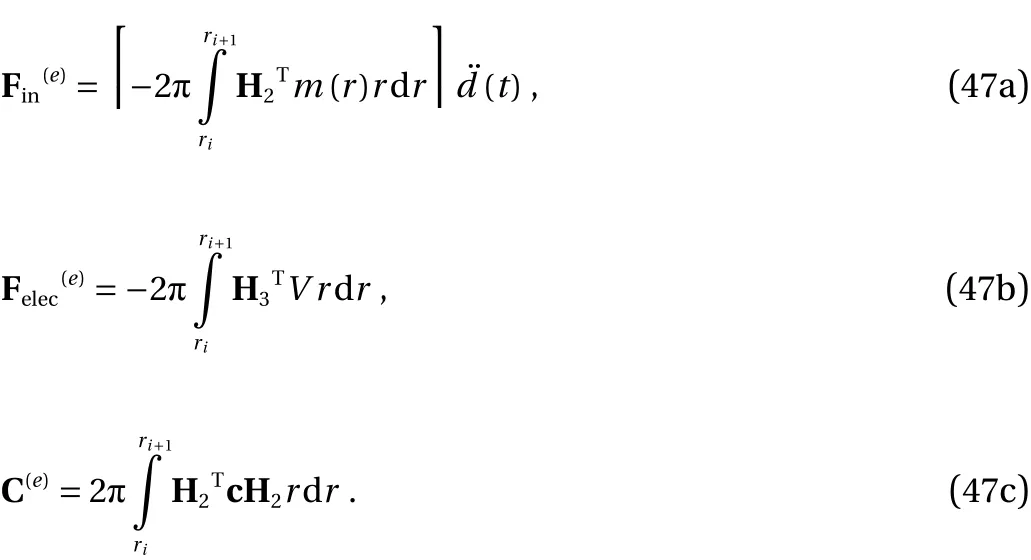
According to Eq. (13) the total charge stored on the electrodes can be calculated by integration of the component of the electric displacement vector along the thickness (D3) over the area which is covered by the electrodes. Ohm’s law indicates that the output voltage of the harvester equates the time derivative of the total stored charge multiplied by the resistance of the connected load. Therefore:

wherenedenotes the total number of the elements which are covered by the electrodes. SubstitutingVfrom the above equation into Eq. (47b), one concludes that the effect of the harvested power which is consumed by the connected resistive load may be presented by a damping matrix as follows:

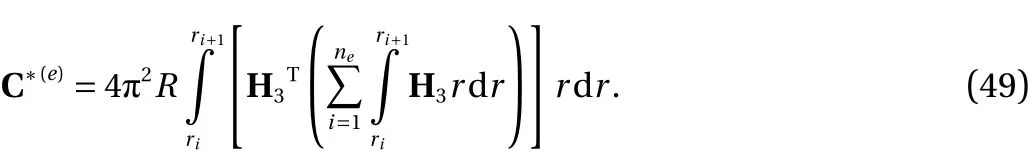
Fig. 2. Structural element used in the FEM simulation a schematic view and b thin-walled ring which is presented by the element

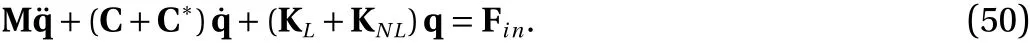
It should be noted that in addition to mechanical boundary conditions which are given in Eq. (16), an electrical boundary condition which indicates thatD3vanishes at nodes which are not covered by the electrodes, should be imposed after assembling the stiffness matrix.

Equation (50) is a nonlinear time-dependent ordinary differential equation which can easily be solved using the explicit finite difference method. To do that the time domain is discretized by introducing a uniformly partitioned mesh and then the derivatives are replaced by their backward difference approximation. Also the nonlinear stiffness matrix is approximated by its value at the previous time step. The following equation is derived for calculating the nodal values at each time step:

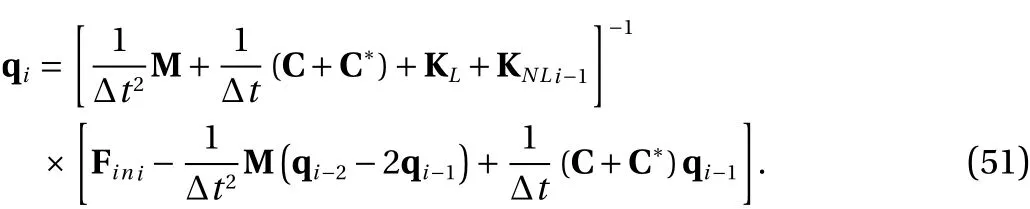
In this section the behavior of the disc-shaped harvester in nonlinear regime is investigated in accordance with the developed model and derived solutions. To this end a laminated piezoelectric circular plate with a brass base layer covered by PZT-5H layers is considered as case study. The geometric properties of the harvester are given in Table 1.

Figure 3 shows the frequency response of the system at the primary resonance. As expected the response curve is bended toward higher frequencies as a result of the hardening nonlinearity due to midplane stretching. The most significant charac-teristic of this nonlinear response curve is that due to bending the slope of the curve changes smoothly and consequently considerable amount of power is generated in a wider frequency interval. This effect leads to enhancement of the operational bandwidth of the nonlinear harvester in comparison to linear types.To examine the validity of our analytical solution the results of the performed FEM simulation are depicted in this figure together with the analytically calculated response curve where a good agreement is observed between them.

Table 1 Geometric properties of the harvester

Fig. 3. Comparison of analytical and FEM solutions at primary resonance (Q =400,R=20 kΩ,ABase=0.5 g)

Figures 4 and 5 depict the frequency responses of the proof mass displacement and output power of the harvester for different values of the input acceleration, respectively. As can be seen in these figures due to nonlinear behavior of the response curves the operational bandwidth of the harvester enhances as the excitation amplitude is increased. However, it should be noted that according to coexistence of two low and high energy stable solutions at excitation frequencies in the neighborhood of resonance frequency, this bandwidth enhancement occurs provided that the system response is converged to the high energy node on the upper branch of the response curve.

For a nonlinear resonator the stable node that the system converges to is dependent on the trajectory of the excitation. In many environments such as industrial machinery the vibration frequency ramps up when the motor is turned on and the machine starts to work. In such environments the response of the harvester automatically falls on the higher energy branch. In general, according to the coupling phenomenon of mechanical and electrical domains in kinetic harvesters, they may be perturbed from the low energy branch to the high energy one either mechanically or electrically employing an external control system [32, 33].

Fig. 4. Frequency response of proof mass displacement (Q=400,R=20 kΩ)

Fig. 5. Frequency response of output power (Q =400,R=20 kΩ)

Figure 6 illustrates the effect of the mechanical quality factor on the frequency response of the system. One other significant advantage of a nonlinear harvester in comparison to linear counterparts can be distinguished from the results presented in this figure. As can be seen in this figure, in a nonlinear harvester the bandwidth increases similar to the peak harvested power as the mechanical quality factor of the system enhances. While in linear devices the harvested power and the bandwidth vary in opposite ways as quality factor changes which necessitates an upper limit on the system efficiency in order that a minimum value of bandwidth is achieved.

As can be concluded from Eq. (38), in the nonlinear regime of operation the peak amplitude of the vibration changes linearly with respect to both excitation amplitude and the mechanical quality factor (which is in turn proportional to the inverse of the damping coefficient). In addition from the governing equations it can be deduced that the excitation frequency is approximately a parabolic function of the vibration amplitude. Due to these facts as evidenced by Fig. 4, the backbone curve of all the curves shown in the figure has a parabolic behavior and also the magnitude of the peak amplitudes change linearly with respect to the applied base acceleration. Since the output power of the harvester as indicated by Eq. (37) is a function of the square of the vibration amplitude, the backbone curves in Figs. 5 and 6 are straight lines. It should be noted that while the peak generated power changes proportional to the square of the applied excitation amplitude as shown in Fig. 5, due to effect of energy harvesting on the vibration damping of the disc, the peak output power is not a function of square of the mechanical quality factor anymore.

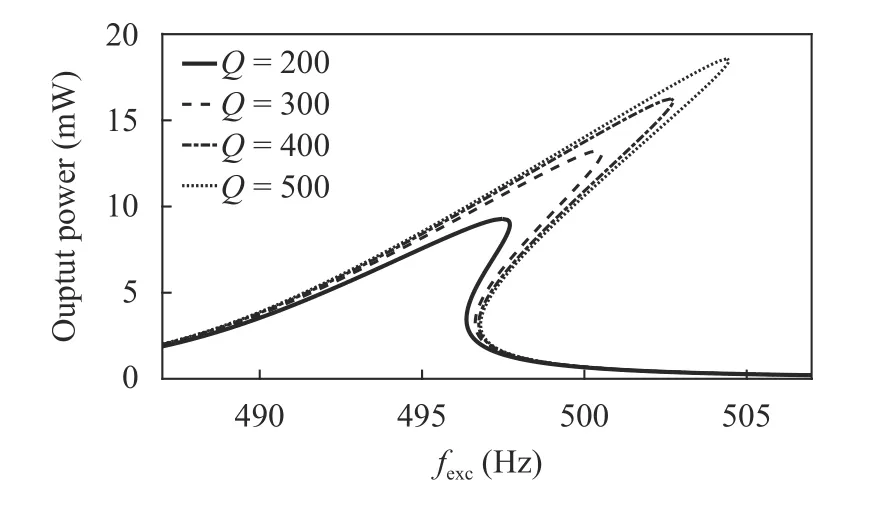
Fig. 6. Effect of mechanical quality factor on the frequency response of output power ( ABase=1 g,R=20 kΩ)

Fig. 7. Effect of mechanical quality factor on the half power bandwidth of the harvester (R =50 kΩ)

Figure 7 shows how the half power bandwidth of the harvester varies as the quality factor of the system changes. For small values of quality factor under a specific amplitude of excitation the system operates in the linear regime and consequently its bandwidth declines as the quality factor increases. When the quality factor reaches a minimum value in accordance to the applied excitation, the system transits to the nonlinear regime.Beyond this point as expected the bandwidth of the system will be enhanced when the quality factor is increased. As can be seen in the figure the transition from linear to nonlinear regime occurs at lower quality factors as the amplitude of input acceleration is increased.

The effect of impedance of external load on both the output power and half power bandwidth of the harvester is presented in Fig. 8. As can be seen in this figure the curve regarding to the output power has two relative maximums occurring at load impedances for which the damping ratio due to harvesting electrical energy from the system equates the mechanical damping ratio. The bandwidth curve has an absolute minimum which occurs when the external impedance connected to the harvester equates the impedance of the equivalent capacitance of the piezoelectric layer at resonance frequency. At this point the peak amplitude of plate vibration is minimized and consequently the effect of nonlinearity on enhancing the operational bandwidth of the system is declined.

To show the effect of nonlinearity on the behavior of the device, the response of the system while neglecting the geometric nonlinearity is presented in the figure as well. As can be seen while the nonlinearity does not have a considerable effect on the harvested power, it has largely enhanced the bandwidth of the system. That’s because the high bandwidth of the nonlinear device is due to the bending of the response curve which does not occur in the linear counterpart. Furthermore, unlike the nonlinear device in a linear harvester as damping increases the resonance peak gets more flattened and therefore the bandwidth increases.

Fig. 8. Peak output power and half power bandwidth as functions of the external load impedance (solid line: nonlinear system,dashed line:linear system)

Nonlinear behavior of a disc-shaped piezoelectric laminated plate implemented as a vibrational energy harvester due to midplane stretching effect is investigated. Coupled electromechanical partial differential equations governing the vibration of the system and the output voltage are extracted exploiting extended Hamilton’s principle. Subsequently, employing Galerkin’s method the derived PDEs are order-reduced to find the ordinary differential equations which are able predict the behavior of the system with a high accuracy. The derived equations are then analytically solved through using perturbation method of multiple scales. Results show that as the system enters the nonlinear regime the operational bandwidth is enhanced considerably due to bending of the frequency response curve. In the nonlinear regime increasing the mechanical quality factor of the system leads to enhancement of both output power and bandwidth of the harvester which makes design and fabrication of high efficiency wideband harvesters possible. Effect of various parameters including quality factor, excitation amplitude and external load impedance on the response of the system is investigated.Verification of the analytical results using a nonlinear electromechanical FEM simulation of the system shows an agreement to a large extent between them. According to the obtained results the considered harvester when operating in nonlinear regime may be efficiently used as an alternative to conventional linear harvesters through effective elimination of the narrow bandwidth characteristic from which linear harvesters suffer.