On plane Λ-fractional linear elasticity theory

K.A. Lazopoulos, A.K. Lazopoulos

a14 Theatrou Str., Rafina, 19009 Greece

bMathematical Sciences Department, Hellenic Army Academy Vari, 16673 Greece

Keywords:Plane elasticity problems Λ-fractional linear elasticity theory Λ-fractional derivative Λ-fractional space Biharmonic function Fractional beam bending

ABSTRACT Non-local plane elasticity problems are discussed in the context of Λ-fractional linear elasticity theory. Adapting the Λ-fractional derivative along with the Λ-fractional space, where geometry and mechanics are valid in the conventional way, non-local plane elasticity problems are solved with the help of biharmonic functions. Then, the results are transferred into the initial plane.Applications are presented to homogeneous and the fractional beam bending problem.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Fractional calculus was originated by Leibniz [1] and in essence, further developed by Liouville [2], Riemann [3],Gründwald [4], and Letnikov [5]. Of course numerous other scientists did minor or major contributions to this ambitious discipline but the five prementioned mathematicians and mechanists contributed the cornerstones of the field. The applications of this mathematical field are vast and touch every aspect of scientific activity: Fractional calculus is vividly present and mostly reliable in problems concerning many scientific fields from Mechanics to economics and from control theory to biomedical sciences and biology [6-11].

The main advantage of this field is non-locality: Fractional Derivatives do not have a local character; they are non-local.Therefore non-local particle interactions may be expressed in a very clear and meaningful way using Fractional derivatives. Especially in micromechanics, Eringen [12] in his excellent treatment pointed out the various reasons of non-local behavior of material deformation.

The other main characteristic of this valuable field is flexibility, since it is often easy to slightly alter the order of the fractional derivative so that the results from the analysis fit experimental data with the most effective way, see Mouzakis and Lazopoulos [13].

Until now, Fractional Mechanics exhibit time fractionality,introduced by Bagley and Torvik [14], and space fractionality, introduced by Lazopoulos [15]. Time fractionality in mechanics has to do mainly with the study of viscoelastic phenomena,Atanackovic and Stankovic [16], and control problems, while space fractionality has to do with the non-local fractional strain with strong non-local character, Lazopoulos [15], contrary to the local character of the conventional strain [17].

However, all the well known fractional derivatives feature an operator's character, instead of a derivative's one. Indeed, no fractional derivative satisfies the prerequisites for defining a derivative according to differential topology [18]

The well-known fractional derivatives violate one or more of the above properties and thus their use in mathematics and physics is questionable.

Eringen [12] in his excellent treatment concerning the Nonlocal theories of continua states in the introduction “Non-localcontinuum field theories are concerned with the physics of material bodies whose behavior of a material point is influenced by the state of all points of the body. The non-local theory generalizes the classical field theory in two respects i) the energy balance law is considered valid globally (for the entire body) and ii) the state of the body at a material point is described by the response functionals”.

Based upon the Λ-fractional derivative and the corresponding Λ-space, the fractional bending beam problem, Lazopoulos[19] has been presented along with the fractional buckling and post-buckling problem of a beam under axial loading [20]. In the present work, the fractional plane elasticity problems will be discussed with the help of the Λ-fractional biharmonic function. In fact the various problems are transferred from the initial plane to the Λ-space, where the initially fractional derivatives are transformed to conventional ones with all the properties of the common derivatives, corresponding to differentials and generating geometry. Solving the plane problem in the Λ-space, the results are transferred to the initial one. Strains may not be transferred into the original space, since they are derivatives having no meaning in the original space.

Since the Λ-fractional derivative is a new idea, some outline of the Λ-fractional theory will be first presented and then the general Λ-plane fractional elasticity theory will be introduced.The theory is applied to homogeneously Λ-fractional deformations in the Λ-space along with the fractional beam bending problem.

Of course one might ask, is there any experimental evidence for the proposed non-local theory? The answer is given by Truedell and Noll [21] in page 4 of Sect. 2. Truedell states, “of course physical theory must be based on experience, but experiment comes after, rather than before theory. Without theoretical concepts one would neither know what experiments to perform nor be able to interpret their outcome”.

Leibniz initiated fractional calculus in 1695, looking for the possibility of defining the derivative dng/dxnwhenn=1/2. In fact he had in mind the extension of his definition of the local derivative to the non-local one. Although Leibnitz was looking for a non-local derivative, satisfying the prerequisites of differential topology, just to correspond to a differential, various fractional derivatives were shown up without those properties. In fact many fractional derivatives appeared and used in physics,mechanics, economics, control etc., without correspondence to differentials and hence unable to generate geometry. Although the need for a non-local derivative was imperative, their inability to generate geometry, due to the lack of the differential kept off many scientists from their use. In fact, although fractional calculus was flourished, the proposed fractional derivatives were in fact operators. Nevertheless many times were used as having the properties of derivatives, able to fulfill principles demanding the existence of differentials. Recently fractional analysis has become a branch of pure mathematics with many applications in physics and engineering.That analysis is non-local, contrary to the conventional one.

The detailed properties of fractional derivatives can be found, among others, in Kilbas et al. [6], Podlubny [8], Samko et al. [7]. Starting from Cauchy formula for then-fold integral of a primitive functionf(x)

It is assumed, in Eqs. (6) and (7), thatγis the order of fractional integrals withm＜γ ≤m+1, consideringΓ(x) = (x-1)! withΓ(γ) Euler's Gamma function.

Yet, some of the most established books in fractional analysis are referred [6-11], just to compare the present version of the fractional analysis to the existing one. In addition, the analysis is simplified when0＜γ＜1. In that case, theγ-multiple integral is defined by

withΓ(γ) Euler's Gamma function.

Furthermore, the left Riemann-Liouville (RL) derivatives are defined by

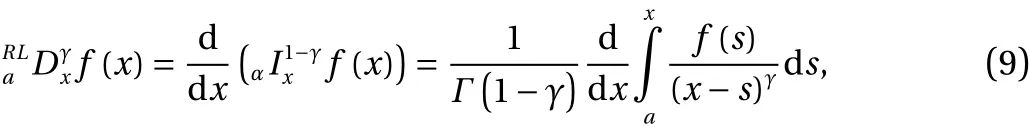
with similar definitions for the right fractional integrals and derivatives [8]. Moreover, the Λ-fractional derivative is defined by

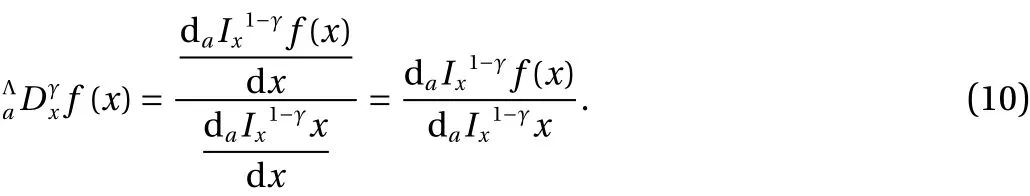
In addition the results from the Λ-space may be transferred to the initial space through the relation

Let us point out that functions may only be transferred from the fractional Λ-space to the initial one. No derivatives may be transferred since fractional derivatives do not exist in the initial space.

The main disadvantage of the existing fractional derivatives is that they fail to satisfy Leibnitz and composition (chain) rules.Therefore they cannot define a differential. Let us point out that Leibnitz in 1695 and many other famous mathematicians, like Liouville, Lagrange, Euler, Riemann and many other scientists as well, were looking for fractional derivatives satisfying the prerequisites of differential topology, generating fractional differential geometry. As a consequence, the use of the various fractional derivatives in mathematical, geometrical and physical problems is questionable. On the other hand, the proposed formulation yields derivatives defining differentials, fulfilling all the necessary conditions demanded by a derivative, according to differential topology. Hence, the proposed fractional Λ-derivative generates a fractional differential geometry, not in the original coordinates but in a coordinate system, which will be defined below.

Following that procedure, various fractional mathematical analysis areas, such as fractional differential geometry, fractional field theory, fractional differential equations etc may be established. The proposed Λ-fractional derivative satisfies Leibnitz's rule for the product of theI1-a f(x) andI1-ay(x). Indeed,

Furthermore, the fractional derivative of a composite function is defined by

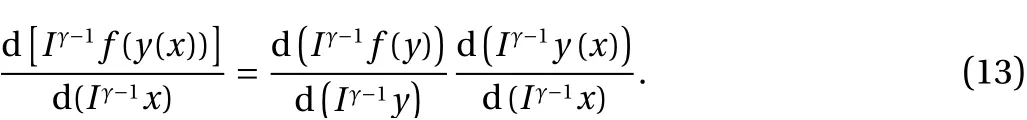
The linearity properties along with Leibnitz's and composition rules, Eqs. (12) and (13), satisfy all the differential topology requirements, Chillingworth [18], for the definition of a differential and fractional differential geometry as well. In fact the nonlocal mathematical analysis is established with derivatives having non-local character.

Let us point out that functions may only be transferred from the fractional Λ-space to the initial one. No derivatives may be transferred since fractional derivative does not exist in the initial space.

Further information of the Λ-derivative and Λ-space with applications to specific functions may be found in Lazopoulos and Lazopoulos [22].

Consider a material bodybwith its boundary ∂bat its undeformed initial placement inxspace. Its current (deformed) configuration isδwith the boundary ∂δ. Α material pointxin the reference placementbtakes the placementψin the current configurationδ, see Fig. 1. Hence, the local deformation is defined by Refs. [17, 23]

In addition, the linear strain tensor is expressed by

where H = F-I is the displacement gradient tensor.

Proceeding to the deformation and strain definitions in the fractional Λ-space, the reference placementband the deformed oneδare represented by the configurationsBandΔin the Λspace through the transformation, see Eq. (8)

In addition the transformationΨ, see Fig. 2 of the current placementψin the fractional Λ-space is given through the help of Eq. (8) by

Hence, the Λ- fractional gradient of deformation is expressed by

Furthert the Λ-fractional linear strain tensor is defined by

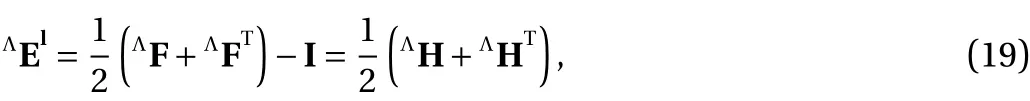
withΛH the Λ-fractional displacement gradient in the Λfractional space.

The various deformation tensors in the Λ-fractional space may be transferred back to the original space through the transformation

The procedure is clarified in the application that follows.

In the conventional plane linear elasticity theory in rectangular coordinates, the solution is defined by the biharmonic equation

with the stress components defined in terms of the stress functionφthrough the relations

Therefore, in the Λ-fractional space, the homogeneous elasticity linear Λ-fractional problem is defined by the biharmonic function

with the Λ-stresses defined by

Since for any constantΘin the fractional Λ-space (X,Y), the corresponding valueθin the initial space (x,y) equals to

Therefore,

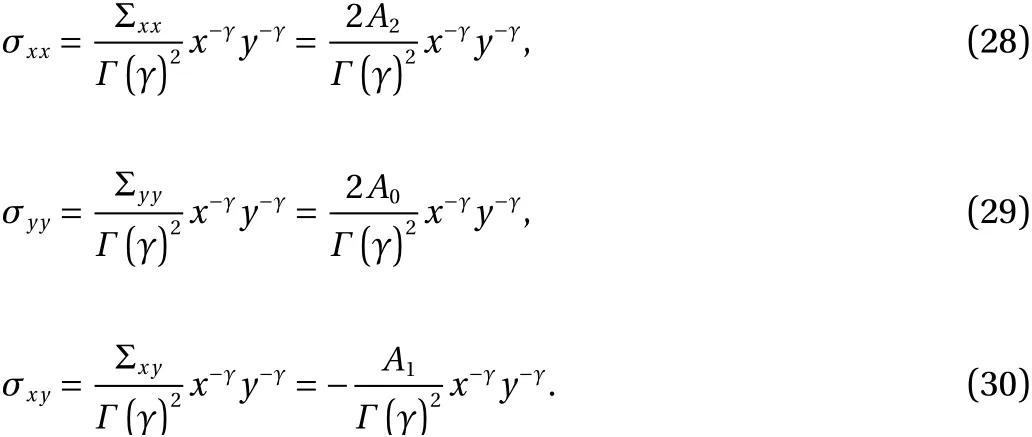
Hence, the traction applied on a body in the initial plane should be governed by Eqs. (28)-(30). Proceeding to the definition of the displacement field the strain in the Λ-space is defined for the plane strain problem by

withνdenoting Poisson's ratio andEYoung's modulus. For zero displacement atx= 0 ory= 0, the displacement functions in the Λ-space are defined by

Since,

Recalling Eq. (20), the displacements (U,V), Eq. (33) in the Λ-fractional space correspond to the displacements (u,v) in the initial plane (x,y) by

Performing the algebra the displacementuequals

It is pointed out that strains may not be transferred in the initial space, since geometry and differential do not exist in that space.

Let us consider a rectangular beam, Fig. 3 subjected to a transverse force f at the free endx=aand built in at the endx=0.The horizontal boundariesy=±bare traction free. In Sect. 5.2.1 of Ref. [23], describes the solution to the problem with the help of biharmonic function.

Following Barber [23], the biharmonic function

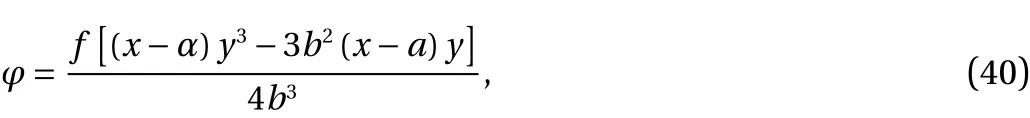
with

Applying the fractional Λ-derivative theory to the present beam bending problem, the Λ-space, see Fig. 4, may be formulated with, see Eq. (34)

Applying the plane elasticity theory with the biharmonic function in the fractional Λ-space we get, see Eqs. (22) and (24)

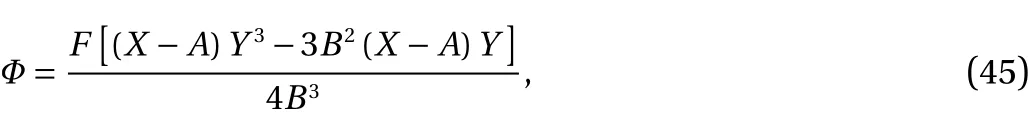
with

Considering Eqs. (20) and (34), the various stresses may be transferred from the Λ-space to the original one. Indeed the stresses ΣXX, ΣXYmay be expressed in thex,yvariables using Eq.(20)

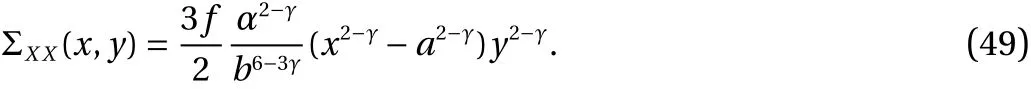
The stresses are transferred in the original space through Eq. (20). Indeed,

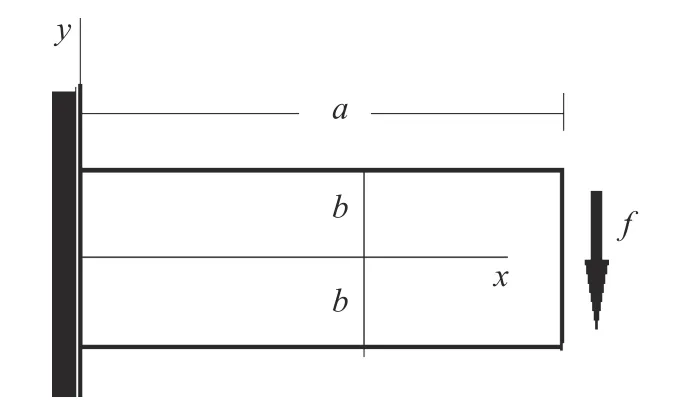
Fig. 3. Initial space of a beam cantilever with its load.

Fig. 4. Λ-space of the cantilever beam.

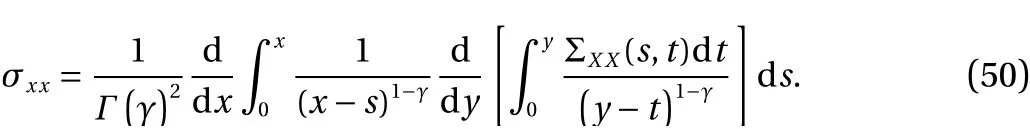
Performing the algebra, the stressσxxis equal to

In Fig. 5-Fig. 7 below, we can see the results for a specific application whereα= 200 μm,b= 5 μm,f= 50 N/m andy=b= 5 μm.

Following the same procedure, the shear stress in the crosssection of the beam is expressed by

Fig. 5. σxx distributed through the length of the beam along the upper fibers for γ=0.8.

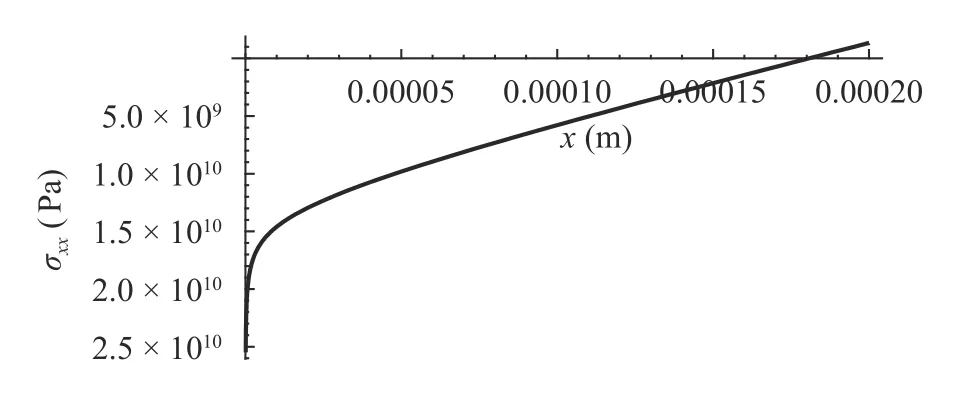
Fig. 6. σxx distributed upon the length of the beam along the upper fibers for γ=0.9.

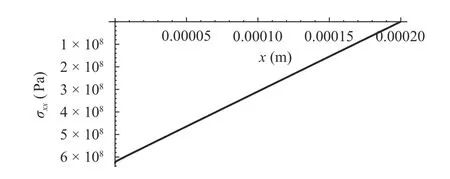
Fig. 7. σxx distributed upon the length of the beam along the upper fibers for γ ≈ 1.0 (conventional case).

Stresses and displacements of plane elasticity problems are calculated using Fractional Analysis. For the calculation of those stresses, the Λ-Fractional Derivative is employed along with the corresponding Λ-Fractional Space. The equation describing the equilibrium of the system in the Λ-Fractional Space is biharmonic, which has the Airy function as its solution. The procedure described in this article is to solve the biharmonic equation in Λ-Space, find the stresses in that space and then transfer the results to the initial space using the proper fractional transformation formulae. Applications are presented to the homogeneous deformations in the Λ-space and the bending of a cantilever beam under force application upon the free end. Further, the displacement fields in the initial space have also been defined in the problem of homogeneous deformations serving as an example for the definition of the displacement fields in the initial space.