Deformation and failure in nanomaterials via a data driven modelling approach

M. Amir Siddiq

a School of Engineering, University of Aberdeen, AB24 3UE, Aberdeen, UK

Keywords:Data driven computational mechanics Nanomaterials Carbon nanotubes Nanocomposites

ABSTRACT A data driven computational model that accounts for more than two material states has been presented in this work. Presented model can account for multiple state variables, such as stresses,strains, strain rates and failure stress, as compared to previously reported models with two states.Model is used to perform deformation and failure simulations of carbon nanotubes and carbon nanotube/epoxy nanocomposites. The model capability of capturing the strain rate dependent deformation and failure has been demonstrated through predictions against uniaxial test data taken from literature. The predicted results show a good agreement between data set taken from literature and simulations.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Material constitutive modelling at various length scales has been under investigation for many decades, however several challenges still exist which are under rigorous research to date.Some of these challenges include, formulation of complex material constitutive models [1-6] which incorporate underlying physical mechanisms, and identification of a large number of material parameters [7-11]. Presently, no unified material constitutive model exists which incorporates all physical mechanisms and their interactions. This is due to the complexities associated with the active mechanisms and their interactions. Therefore, depending upon the active mechanisms and length scales different material constitutive models exist. These models can be classified into many different types, for example due to mathematical principles being used (for e.g. variational principles [4]), or to incorporate specific microscale phenomenon [12], or to simulate specific type of manufacturing process [13, 14].

Recently, a number of researchers have developed data driven (DD) computing in the context of boundary value problems[15-21] and nonparametric regression approach [22]. Such approaches directly use the experimental data and eliminate the efforts, uncertainties and errors induced during inverse modelling to generate stress-strain curves. Kirchdoerfer and Ortiz [15,21] presented a new paradigm of data driven computing by eliminating material constitutive modelling and using experimental data directly. Nguyen and Keip [18] presented a similar approach to nonlinear elasticity. Leygue et al. [16, 23] used experimentally measured strain fields to build a database of stressstrain fields which were then used to predict the behaviour of one- and two-dimensional solids.

In the present work, data driven approach presented in Refs.[20, 21] is extended and implemented in the context of boundary value problem using linear finite element methods. As compared to previous works, this research deals with more than two state variables, i.e. stresses, strains, strain rates, and failure, of nanomaterials.

The classical formulation has been discussed elsewhere (for details see Refs. [15, 20, 21]) and is not repeated here for brevity.A brief summary of the model with emphasis on the extension is discussed in the following. Data driven framework is implemented in the context of linear finite element methods. Starting with the corresponding phase space for three-dimensional boundary value problem, which comprises of set () of stresses,strains, strain rates, and failure stress, respectively. For the threedimensional problem the corresponding phase space is assumed to be 19 dimensional with σ, ε, and ε˙ are six dimensional each whereas σfis scalar.

A discretised finite element model with linear elements of a nonlinear elastic solid is considered as a starting point. Each element (e) is comprising ofNnodes andMgauss points. The discretised model undergoes displacements u which is given by u=ξa(x,y,z)uawith sum onaanda= 1,2, ...,N.Where uabeing nodal displacement due to appliednodal forces fa,andξaare the interpolation (shape) functions which are based on linear element.

For a known material dataset, i.e. local phase space (Me),data driven framework searches for optimal local state of each element of the material or structure while at the same time satisfying compatibility and equilibrium, viz.

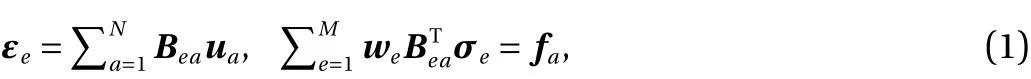
where Beais strain matrix and corresponds to the finite element mesh geometry and connectivity.

As mentioned above, material data set (Me) can be comprised of a number of state variables (βi,i= 1, 2, …,n). For the present workn= 19, i.e. stresses ( σ), strains ( ε), and strain rateswith six components each, and scalar failure stress ( σf), respectively, are known material states.

For the current multi-state data set, following penalty functionFeis used

with the minimum is searched for all local states in the data set(Me). HereCiis a numerical value and does not represent a material property. Overall objective of the solver is to minimise the globalFby enforcing conservation law and compatibility constraints

withwebeing the weight factor which is the volume of the elementein undeformed configurationVoe.

Equations (2) and (3) eliminate the traditional material modelling step which requires material constitutive law,comprising of a number of unknown material parameters which are required to be identified through inverse modelling [8, 9, 11, 24, 25].

Finally, general form of equilibrium constraint is given by

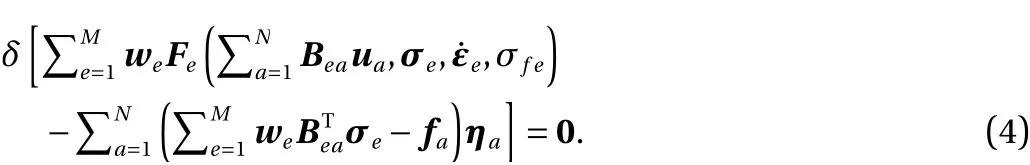
Following standard procedure of taking possible variations, a system of linear equations is obtained for nodal displacement,the local stresses and the Lagrange multipliers and is given by

Note: For dynamic analyses, inertia can be incorporated separately as

Once all optimal data points are determined, Eq. (5) is used to define nodal displacements, the local stresses and the Lagrange multipliers.

The applicability of the presented formulation is demonstrated by performing simulations on deformation and failure in carbon-nano-tubes (CNT) and CNT/Epoxy based nanocomposite materials. All simulations are based on static analyses in the context of finite element methods using Eq. (6) and linear interpolation (shape) functions. Brief description of individual experiments, molecular dynamic simulations and results are presented in the following.

Kok and Wong [26] performed molecular dynamics (MD)studies on single-walled carbon nanotubes (SWCNT) and double-walled carbon nanotubes (DWCNT) to evaluate their mechanical properties. Mechanical properties were estimated for various aspect ratios and strain rates. For the present study,MD results for (5, 5) armchair SWCNT at different strain rates were used. For model application purposes and to check the handling of data size by presented model, data for different strain rates was used to generate the stress strain curves for unknown intermediate strain rates (see surface plot in Fig. 1). At continuum scale, carbon nanotubes have been modelled as shells [27], beam [28], and a combination of many truss elements [29] (for details and other literature please see references there in). To demonstrate the application of the presented data driven formulation a similar approach has been used, i.e. by modelling the SWCNT as a single truss element under tensile loading. Comparison between MD generated stress strain response and model predictions for three different strain rates are shown in Fig. 1. Results show a very good agreement between MD simulations and DD model response for multi-state material dataset.

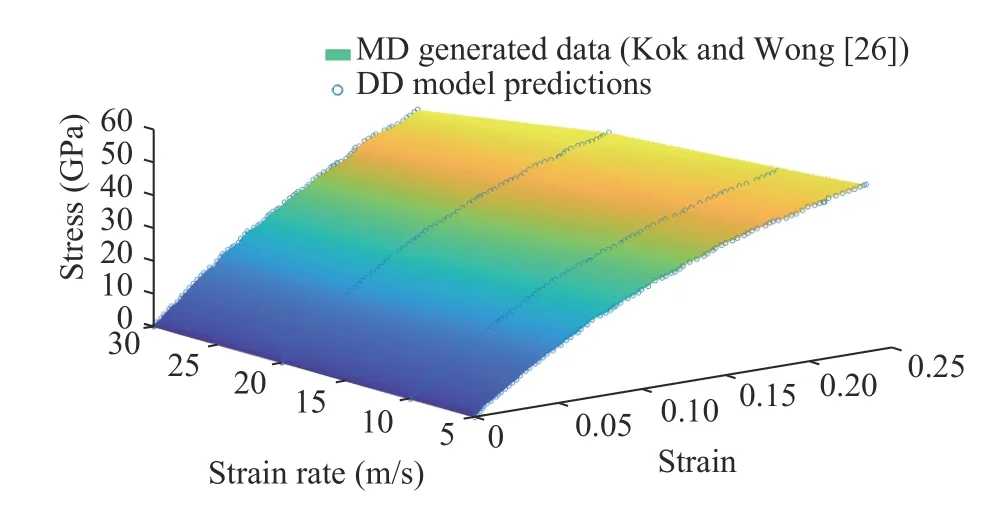
Fig. 1. Comparison of data driven model prediction and MD generated data of SWCNT from Kok and Wong [26]

Nahm [30] performed tensile testing of MWCNT using a nanomanipulator and sub nano-resolution force sensor in scanning electron microscope (SEM). As explained previously, MWCNT was modelled using a truss element. Comparison of experimental and predicted stress-strain response are plotted in Fig. 2 showing a very good agreement up to the final failure of the nanotube without using any material constitutive model and directly using experimental data.

Yu and Chang [31] performed experimental studies to understand tensile behaviour of MWCNT-reinforced epoxy-matrix composites. Effect of the weight fractions and diameters of CNT's on stress-strain behaviour, and strength was investigated.For the model application purposes, CNT/epoxy composite with 1% MWCNT weight data is used. Uniaxial tension test is simulations using three-dimensional eight node cube element with one integration (gauss) point. A comparison between model predictions and experimental results are presented in Fig. 3 showing a good agreement.

Finally, in order to demonstrate the application of the proposed data driven model to finite elementbased analysis and to show the models ability to capture realistic fracture patterns during deformation; a finite element model of dog-bone sample is used. The sample is based on ASTM D638 which was used by Yu and Chang [31] in above example. Experimental data from Fig. 3 is directly used without using any material constitutive model or material parameters. Model was discretised using 4488 reduced integration eight node hex elements. Displacement boundary condition of 1.0 mm/min as used during experiments was prescribed. Contour plots of the von Mises stress at different stages of the deformation are plotted in Fig. 4 showing the presented DD model's capability of predicting the stresses and macroscopic fracture without any numerical difficulties.

A data driven computational method for predicting mechanical response for nanomaterials was extended and used to predict the deformation and failure in nanomaterials. Numerical predictions were presented using the developed data driven model and showed a good agreement with the data set taken from experiments and molecular dynamics simulations. Presented model is applied in the context of nanomaterials, however it can be applied to any length scale. As a future work, the model is further extended to account for plasticity in the context of microscale slip in single crystals. Current crystal plasticity models require a large number of parameters which can be avoided if material data set can directly be used to account for microscale plasticity which is under development and will be reported in near future.

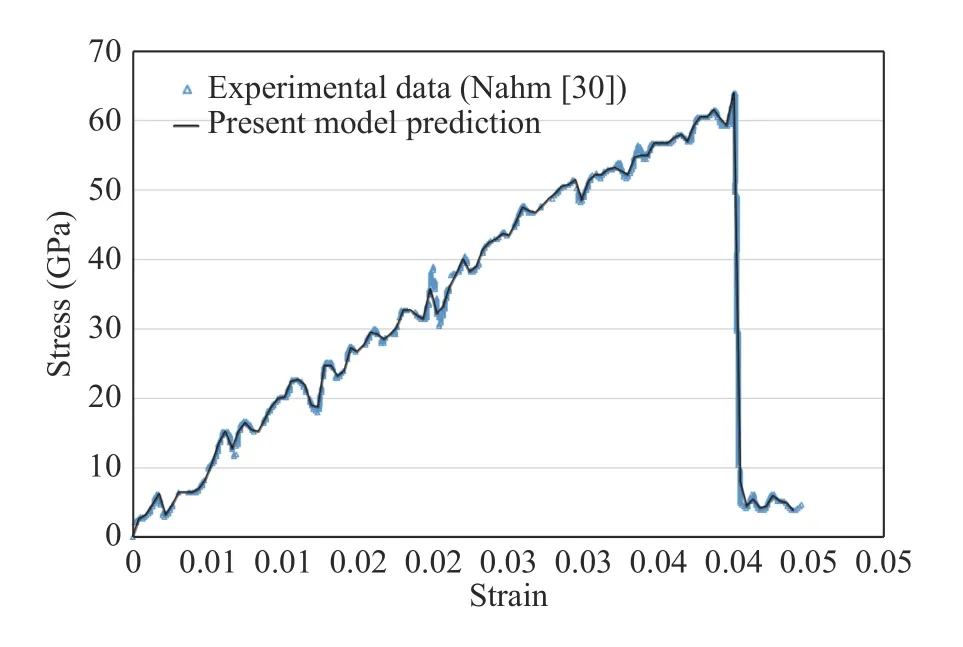
Fig. 2. Comparison of data driven model prediction and experimental data reported in Nahm [30] for MWCNT

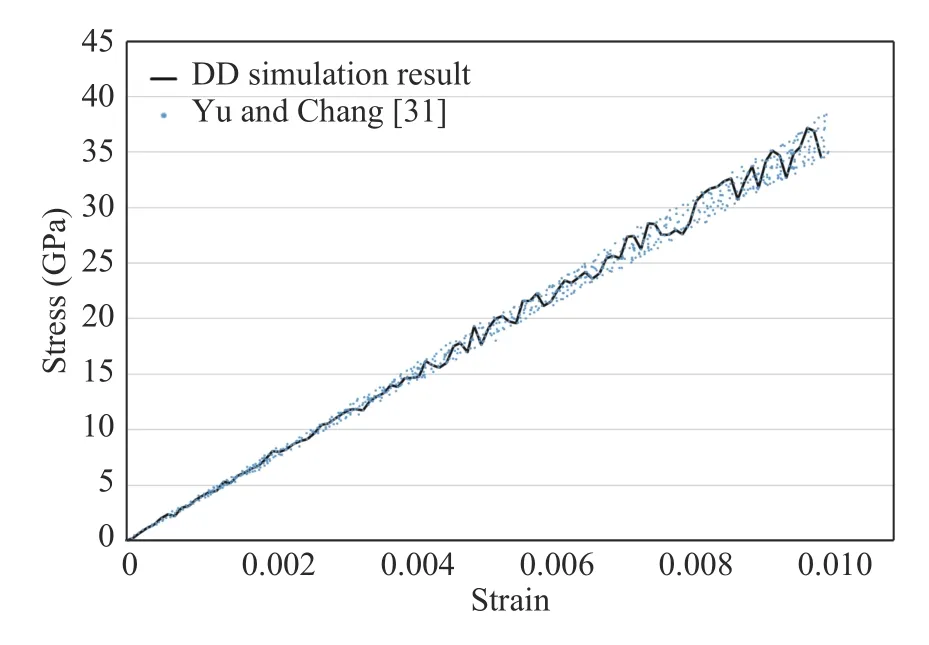
Fig. 3. Comparison of data driven model prediction and experimental data of CNT/epoxy composite (1% MWCNT weight fraction)reported in Yu and Chang [31]

Fig. 4. Mechanical response and failure in CNT/Epoxy Composite with 1%wt fraction of CNT under uniaxial tensile loading