Particles-induced turbulence: A critical review of physical concepts,numerical modelings and experimental investigations

Guodong Gi, Abdellh Hdjdj, Sergey Kudrikov, Olivier Thomine

aDEN-DM2S-STMF, CEA, Université Paris-Saclay, France

bUniversity of Normandy, INSA, CORIA UMR-6614 CNRS, 76000 Rouen, France

Keywords:Particle-induced turbulence Turbulence modulation Physical and numerical modeling

ABSTRACT The presence of solid particles or water droplets in continuous fluid flow can either induce turbulence attenuation or amplification. The modification of the state of the turbulence depends on the characteristics of the particles, such as volume fraction, mean diameter, mass density, or carrier phase flow properties. In this brief review, the main physical concepts related to the most important physical aspects of turbulence modulation are summarized. Different criteria used to distinguish the enhancement or the attenuation effects of the particles on the carrier phase flows are recalled. For the interest of large-scale industrial applications, several theoretical,experimental and empirical approaches are discussed, which provides an interesting framework for the study of the effect of particles on turbulence behavior modification.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

In particle-laden flows, the presence of particle cloud can have two opposite effects on the turbulence state of the carrier flow: either attenuation or enhancement. The modulation of turbulence in the presence of particles can be regarded as a phenomenon induced by several factors such as the distortion of the carrier phase velocity gradient, the streamline curvatures, the vortex shedding of the particles or the damping of turbulence motion by particles induced drag forces [1]. Experimental investigations on dispersed two-phase media mainly focused on the measurements of the mean flow velocity and the Reynolds stresses of the carrier-phase flow. Higher-order statistics such as Lagrangian particle-velocity correlations, carrier-phase turbulent dissipation and phase-phase velocity correlations are also studied [2].

In terms of experimental measurements, the hot-wire anemometry technique was widely used in gas-droplet jets [3] to measure the flow velocity in the particle-laden flow. An example of a water spray and a spray-induced turbulence vortex under an injection nozzle is given in Fig. 1. Later on, a Laser Doppler Velocimetry (LDV) technique was used to better characterize the topology of turbulent flows in the presence of particles. This technique relies on the use of small-particle seeds as tracers to measure the motion of the carrier flow. It was shown that larger dispersed particles produce a stronger signal, that can be discriminated from the carrier phase. For the gaseous carrier phase,the tracers typically have diameters of O (1) μm, while the dispersed particles have larger diameters of O(10-1000) μm [2].

Kulick et al. [4] studied experimentally the effects of particles on the fully developed turbulent pipe flows for different particles with sizes smaller than the Kolmogorov length-scaleη. The particles were found to attenuate the turbulence when increasing the Stokes numberStand the mass loading. Reduction in turbulence intensity was found to be larger in the cross-flow direction compared to the stream-wise direction. The experiments were modeled by Yamamoto et al. [5], with particular emphasis on particle-particle and particle-wall interactions. It was shown that these two interactions played a key role in the turbulence attenuation. Other experiments were also conducted by Paris [6] in a vertical fully-developed channel flow with particles smaller thanη. It was found that the mass-loading ratio increases the effect of turbulence attenuation at low particle Reynolds numbersRepwhose definition is given in Eq. (1). The latter was revealed to be an important parameter for turbulence attenuation. It was concluded that modifications of the carrier-phase turbulence structure by particles are significantly important in turbulence attenuation of particle-laden channel flows.

Measurements of air and particle velocities of the two-phase flow in a vertical pipe were also performed by LDV [7]. It was seen that large particles increased the air turbulence throughout the pipe section, while small particles reduced it [8]. The turbulence was amplified around the pipe center and damped near the wall, which was also reported in Refs. [9, 10]. Kussin and Sommerfeld [11] came to the same conclusion for particles with a diameter larger thanηin horizontal pipe flows.

From experimental point of view, five key factors appear to contribute to the turbulence modulation induced by particles[1]. (1) Surface effects: particle size normalized by a length scaledp/lt; (2) Inertial effects: flow Reynolds numberReand particle Reynolds numberRep; (3) Response effects: particle response timeτpor Stokes numberSt; (4) Loading effects: particle volume fractionαp; (5) Interaction effects: particle-particle, particlewall.

In the following, we will discuss different parameters used for the classification of turbulence modulation.

Gore and Crowe [8] summarized the experimental investigations of turbulence modulation, including jets, pipes, gasparticle and gas-liquid flows. A general trend indicates that small particles (dp＜ 200 μm) contribute to turbulence attenuation,while large particles (dp＞ 200 μm) tend to enhance turbulence.The criterion proposed by Gore and Crowe [8] is based on the ratio of particle diameter to turbulence length scale,dp/lt.

The summarized data is shown in Fig. 2. For various types of particle-laden flows, a fairly distinct valuedp/lt≈ 0.1 was noted below which the particles enhance turbulence dissipation and above which the turbulence is amplified. The behavior of particles in turbulent flows is thought to be similar to grid-screen turbulence. This rough criterion is widely approved in Ref. [12].Many researchers report that the attenuation of turbulence occurs fordp/lt＜ 0.1 [1]. A wide range of experimental observations is made in Ref. [8] including jet and pipe flows with various orientations, at flow Reynolds number ranging from 8000 to 105,density ratio between 0.0012 and 2500 and volume fraction between 10-6and 0.2.

Elghobashi and Truesdell [13] proposed a length-scale ratio ofdp/η, which was also used as a classification parameter in Refs. [2] and [14]. It is widely agreed that the particle size plays an important role in the turbulence modulation [15] and the particles ofdp/η≪ 1 have little influence on the turbulence modulation of the particle-laden flows. Sato et al. [16] claimed that the interparticle spacing can also be considered as a critical parameter for turbulence modulation.

The particle Reynolds number,Rep, which is the ratio of inertial to viscous forces is much used when dealing with particle turbulence modulation. Clift et al. [17] argued that, in a particleladen flow, the wake instability occurs atRep≈ 130 and the vortex shedding starts atRep≈ 270. Hetsroni [10] used the experimental data of Ref. [8] and proposed another criterion based on the particle Reynolds number, defined as

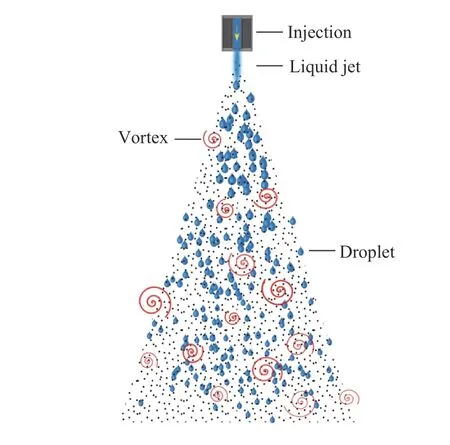
Fig. 1. Schematic representation of a liquid jet spray issuing from an injector nozzle and inducing spray-turbulence generation with vortex formation.

Fig. 2. Percentage change in the turbulence intensity as a function of the ratio of particle size to turbulence length scale, dp/lt, from a wide range of experiments. Adopted from Gore and Crowe [8].

whereµis the dynamic viscosity,ρis the mass density,uis the velocity,dpis the diameter. The subscriptspandfdenote particle and fluid properties, respectively. Hetsroni [10]suggested that flows with high particle Reynolds numbers,Rep＞400, would induce vortex shedding instability that enhances the turbulence intensity. The energy from the average velocity is transferred to higher frequencies. However, it was reported by Geiss et al. [18], that evident turbulence production can also be observed atRepless than 400. A lower critical value of vortex sheddingRep≈270 was proposed as the value which distinguishes the two opposite effects. Despite this difference in critical values ofRep, the study of Ref. [18] confirms the order of magnitude estimated in Ref. [10]. It was argued that the vortex shedding cannot be the only explanation for the enhancement of turbulent intensity [12].

The Stokes number characterizes the behavior of particles evolving within a carrier flow. It is defined as whereτpis the particle response time andτkis the Kolmogorov time scale defined asτk= (ν/ε)1/2,νbeing the kinematic viscosity andεthe mean rate of dissipation per unit mass of fluid. The smaller particles just follow the streamline and behave like tracers of the carrier phase, while the larger particles separate from the carrier flow. Ferrante and Elghobashi [19] used the Stokes number to characterize the turbulence modulation. It was shown that for particles withSt≪ 1, the viscous dissipation rate is larger than those in particle-free turbulence. In this case,the particles denoted ghost particlesSt≈ 0.25 are considered to bring neither amplification nor attenuation to the turbulent kinetic energy (TKE). For larger Stokes numberSt＞ 1, both turbulent length and time scales grow faster. For particles withdp/η≈ 1, the observations yield an increase in the rate of TKE dissipation and a corresponding reduction of turbulence [20].

It was argued that the Stokes number is not the main-driver parameter of turbulence modulation [21, 22], since the turbulent intensity can be attenuated even forSt＜ 60.

The volume fraction of particles,αp, is a parameter widely used to describe the number of particles in a given volume,closely related to the interparticle distance and the particle mass loading. An illustrative classification in terms of volume fraction is given by Elghobashi [23] and shown in Fig. 3.

Three regimes of turbulence modulation are proposed [23].Forαp＜ 10-6, there is a large distance between the particles to have a significant effect on the carrier phase and the interaction is governed by a one-way coupling. The individual effects of the particles are considered. For particle volume fractions in the range of 10-6to 10-3, the amount of particles starts to influence turbulent modulation or modification of the carrier phase. This is referred to the two-way coupling regime. For clouds withαp＞10-3, the interactions among particles such as collisions or droplets coalescences become an important factor in the turbulence modulation. This is known as four-way coupling regime.

Other researches [24-26] argued that even with a very small volume fraction, the dispersed phase can still influence the turbulence in the carrier phase. However, the volume fraction solely cannot clearly discern the attenuation or the enhancement of turbulence.

Tanaka and Eaton [21] mapped out 30 experimental databases, from the open literature with different values ofReandSt(see Fig. 4). The particle momentum number,PaSt, was proposed in Ref. [21], by solving dimensionless particle-laden Navier-Stokes equation [27, 28]

The collapsed turbulence modulation data for various particle-laden flows show that turbulence attenuation occurs for 103＜PaSt＜ 105, whereas turbulence augmentation was lower forPaSt＜ 103and higher forPaSt＞ 105. A weakness in the experimental databases is noted, since there are no turbulence modulation experiments at higher Reynolds number than 3×104.Moreover, it can be mentioned that only the Stokes drag force is considered for the turbulence modulation, which is not able to describe the effects of the vortex shedding [29]. Using the relation between the turbulent length scale and the Kolmogorov length scalelt/η≈Re3/4, Lohse [30] suggested that the particle momentum number can be written as

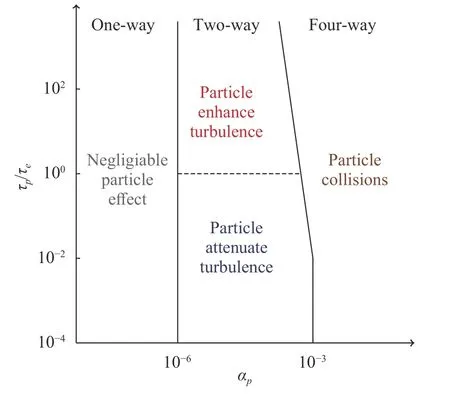
Fig. 3. Map of different regimes of interaction between particles and turbulence [23]. τp is the response time of particles, τe is the turn-over time of large eddies defined as τe=lt/urms where lt is the integral length scale is the root-mean-square velocity.

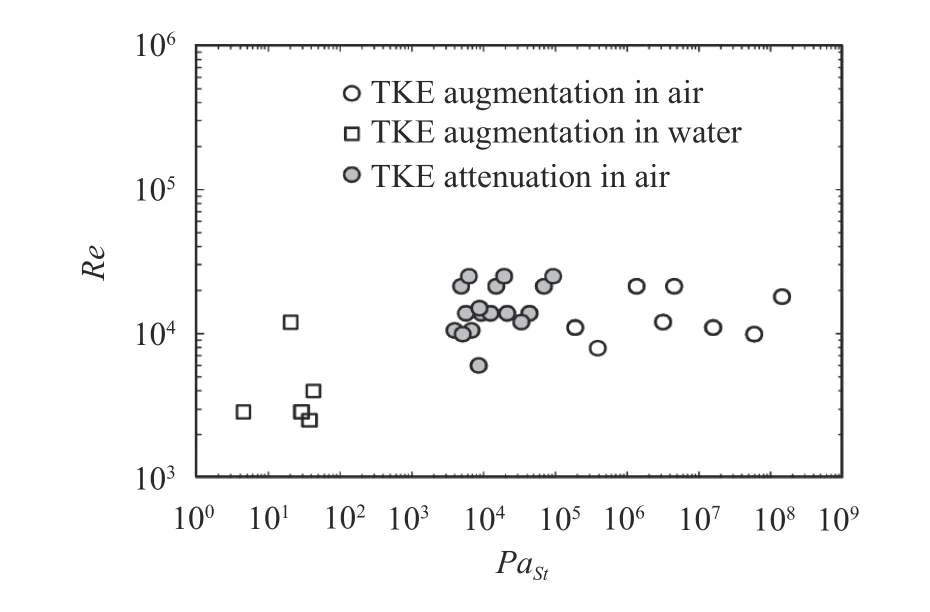
Fig. 4. Mapping of the turbulence modulation experiments based on PaSt and Re [21].

Another rescaling of the particle momentum number is proposed by Luo et al. [29]. The ratio ofStoverPaStis used as a critical parameter to distinguish the attenuation and the enhancement of turbulence

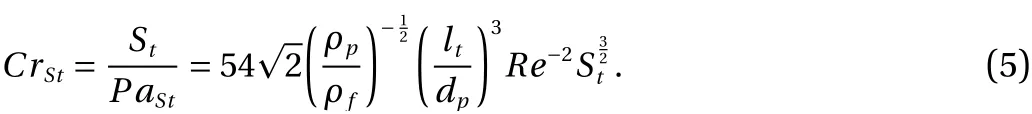
In general, as discussed by Tanaka and Eaton [21], more data is required before a decisive conclusion can be made. At the moment, there exists no broad consensus in Ref. [20] regarding a unique dimensionless number that can perfectly describe the influence of particles in turbulence modulation.

Several numerical approaches have been developed to study turbulence modulation associated with dilute particle-laden flows. However, there is still a lack of suitable models that can account for most important physical factors [31]. The mechanisms of turbulence modulation are not well understood [1] as a result of the complex process of fluid-particle interactions. According to Crowe et al. [1], the actual research trend has focused mainly on the development of either two-equation, or full Reynolds stress models. For large scale industrial applications, the Reynolds-averaged Navier-Stokes (RANS) models are still applicable. However, the use of more sophisticated modeling approaches such as large eddy simulation (LES) or direct numerical simulation (DNS) is prohibitive given the excessive amount of required computational resources. Therefore, reduced-order modeling strategies taking into consideration the main effects of turbulence modulation are of great interest for large-scale engineering applications.

Yuan and Michaelides [32] developed a rather simple mechanistic model for the prediction of turbulence modification in particle-laden flows based on the interaction of a single particle with turbulent eddies. Two predominant mechanisms of turbulence modulation are identified: (1) the dissipation of energy from a turbulent eddy that damps the turbulence; (2) the flow velocity redistribution disturbance due to vortex shedding is important for the enhancement of the turbulence. The derived model is based on the particle size, the relative velocity, the Reynolds number and the density differences between the two phases. The mean rate of turbulent dissipation of the carrier phase flow by the acceleration of the particles is given by

whereltis the eddy size, estimated experimentally [33].

The mean turbulent energy production rate is given by

where G(Lw) is a length-scale function linked to the region behind the particle, andLwis the effective length of the wake[17]. It was reported by Crowe et al. [1] that the production term in Eq. (9) is related to the direction and the magnitude of the relative velocity between the two phases. However, the particle concentration effects are not described. The source term acting on the turbulence modulations given by

which describes the turbulence energy variation due to the presence of particles. This source term can be used to characterize the modification of the carrier phase turbulence intensity in large-scale simulations. The resulting model was reported to show good agreements with the experimental data of Tsuji et al. [7] as depicted in Fig. 5a.

Yarin and Hetsroni [34] proposed a simplified theory to study the effects of particle size on the turbulence modulation in dilute particle-laden flows. Two sources of turbulence are considered: (1) the carrier fluid velocity gradients and (2) the turbulent wake behind coarse particles. The modified mixing-length theory and the turbulent kinetic-energy balance were combined together to derive a simplified model to quantitatively describe the process of turbulence dissipation and generation in particleladen flows

whereu′ is the fluid fluctuating velocity,is the particle relative velocity,γis the mass content of the particles in the fluid element,ρpf=ρp/ρfis the particle to carrier phase density ratio,Ceis an empirical constant andCDis the drag coefficient expressed asEquation (10) can give an estimation of the modification of the carrier-phase turbulence in presence of particles. The effects of particle size are given by the relation [34]

whereΩ≈ 1 is an empirical constant. Equation (10), referred as the “4/9-power” law by Yarin and Hetsroni [34], indicates that particles with larger diameters can enhance the turbulence intensity of the carrier phase. This relation holds only for dilute particle-laden flows, with a small volume fraction of particles.Figure 5b shows the dependence of the carrier fluid velocity fluctuations on. The prediction given by Eq. (10) shows a good agreement with the experimental data of particle-water flow [35] and particle-air flow [36].

For fully developed dilute particle-laden flows in a vertical pipe, Crowe [37] simplified the volume averaged turbulent kinetic-energy equation by taking into account the turbulence generation of velocity gradients (VG), generation by particle drag (PD)and the viscous dissipation (VD), and obtained

whereαis the volume fraction andρis the fluid density. As mentioned above,fandpdenote the properties of the carrier phase and the particles, respectively.iandjare tensor notations.〈ui〉 is the volume averaged velocity and 〈 δui〉 is the deviation from the volume averaged velocity, F is the ratio of the particle drag to the Stokes drag and 〈 ε〉 is the mean viscous dissipation rate of the turbulent energy. For high Reynolds number flows,the drag factor F can be approximated as [37]

whereτpis the response time of the particles andgis the gravity acceleration.

By assuming that the volume fraction of the particle is very small,αp≪ 1 (αf→ 1), the ratio of the inherent length scaleLiand the hybrid length scaleLhgives [37]

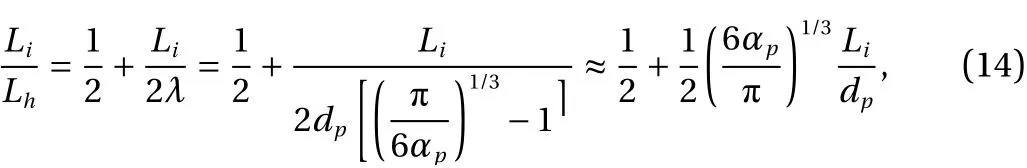
with the hybrid length scale defined as [38]

andλbeing the mean inter-particle distance of the dispersed particles.

Combing Eqs. (12)-(14), the author obtained the turbulence energy modulation given by

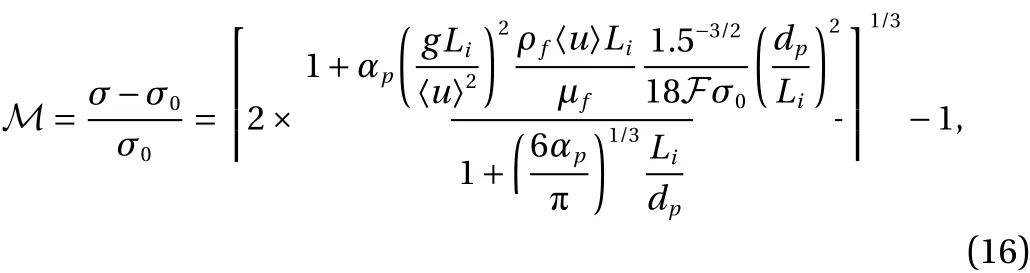
where 〈u〉 is the velocity of the carrier phase, σ =u′/〈u〉 is the turbulence intensity of the particle-free flow andσ0represents the intrinsic turbulence intensity without spray. Positive and negative values of the turbulence modulation factor M correspond to the enhancement and the attenuation of the carrier phase turbulence, respectively. It should be emphasized that, using the hybrid length scale definition Eq. (15), the Eq.(16) has a difference of factor 2 with the one proposed by Ref.[37].

It can be noted from Eq. (16) that the ratio of particle size to turbulence length scale,dp/Li, plays an important role in the turbulence modulation, in accordance with the observations made by Gore and Crowe [8]. Moreover, the gravity of particles has also an important effect on the turbulence modulation through the Froud number,Fr=gLi/u2. One can also see the effects of volume fraction,αp, in Eq. (16). Figure 6 compares the model performance with the experimental data. It is seen that the model can predict the general trend of the turbulence modulation,supported by different experimental data [37].

Equation (16) is used to compare the model prediction with experimental results in Ref. [12]. The parameter M in Eq. (16)seems to provide a poor fit to the experimental data for small values ofdp/Li. An exponential decay term is added to M , such as

where C=-7 ×10-6.It is seen that the modified parameter Mmprovides a better fit with some of the experimental data of Mandø [12].

Fig. 5. a Comparison of Yuan model and experimental values for a pipe flow [32]. b Carrier phase fluctuations of homogeneous turbulence prediction by Yarin theory [34].

Mandø [12] have investigated the effects of large spherical particles (900 μm ＜dp＜ 2000 μm) on the turbulence modulation of the gaseous carrier phase. An empirical correlation based on the compilation of a large amount of experimental data is proposed for the estimation of the modulation strength due to the presence of solid particles in gaseous flow. This correlation is expressed in terms of M as

wherem˙pis the particle mass flux defined asm˙p=αpρpupAswithAsbeing the cross-sectional area of the particle stream. This correlation is claimed to be valid for volume fraction between 2 × 10-5≤αp≤ 1 × 10-3, mass loading between 0.5 to 1.7; particle diameter between 0.9 mm and 1.8 mm anddp/ltratios between 0.1 and 0.5.

Luo et al. [29] have made efforts to obtain quantitative description of the turbulence modulation through the multivariable linear regression formulation of selected experimental data[4, 7, 11, 39]. An empirical formula is obtained for the estimation of the magnitude of the turbulence modulation

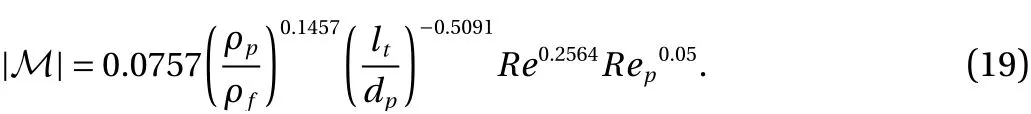
This correlation is reported to match the experimental data with a relative error lower than 25%. Both attenuation and enhancement effects due to the presence of particles can be distinguished by either the particle momentum numberPaStorCrSt.However, the direct comparison between empirical formulations and experimental data was not provided.

Fig. 6. Comparison of model predictions and experimental data for turbulence modulations for particle-laden flow in a vertical pipeis the mass ratio of dispersed particles to the carrierfluid.

Kenning and Crowe [38, 40] proposed another simple mechanistic model to account for the turbulence modulation through the turbulent kinetic energy balance. As shown in Fig. 7, four sources of turbulent energy of the carrier phase are considered:the inherent turbulence of the carrier phase, the turbulence generated by the dispersed particle motion, the inherent viscous dissipation of the carrier phaseand the dissipation due to the drag of dispersed particles. The transport equation of TKE rate is [38]

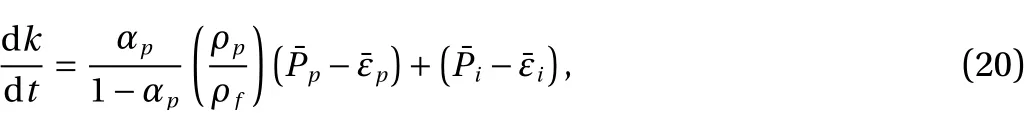
wherekis the turbulent kinetic energy. The expressions for production and dissipation terms can be found in Ref. [38].

Considering that the particles cannot only generate turbulence but also change the dissipation of the carrier flow, Kenning [38] proposed a formalism of turbulent energy dissipation by particles such as

Using M as a dimensionless parameter, one can note that the turbulence is attenuated if M ＜0 and strengthened if M ＞0.Mcan be deduced from

The Kenning's model predicts that the turbulence can be attenuated with small value ofLh. A comparison of the turbulence intensity ratioMand the experimental data of Refs. [7, 39, 41]shows good agreements. However, an extension of the model is needed for comparison with more recent experimental data [37].

In this study, two examples of calculations are performed to investigate the effects of these parameters. The results are shown in Fig. 8(a, b), where the evolution of the turbulence density is plotted as a function of the mean diameter of particles using Kenning's model [38].

It is found that small particles with higher slip velocities can have more important mitigation on the carrier flow (see Fig. 8a).

Figure 8b shows the influence of the volume fraction of particles present in the two-phase flow. The range of water spray density varies between 10-5≤αp≤ 10-3, which is commonly used in the nuclear power plant spray systems for different accident scenarios. It is interesting to notice that the evolution of the turbulence modulation parameter is more sensitive to smaller volume fraction of particles. The attenuation and enhancement effects become more evident in this case.

The particle momentum number,PaSt, is calculated and compared with Kenning model. The transition from attenuation to enhancement with the increase of particle diameterdpis shown with a red dashed line in Fig. 8b.

Fig. 7. Schematic model for turbulence modulation [40].

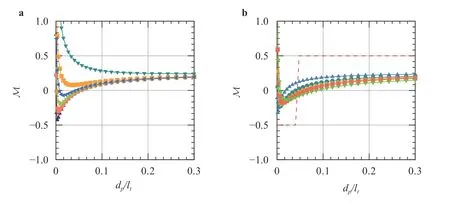
Fig. 8. Results from current numerical simulations of turbulent modulation as a function of mean particle diameters for a different. a Relative velocities = 5.0 m/s. b Volume fractions of particles αp = 1 × 10-5, αp = 2 × 10-5, αp = 3 × 10-5, αp = 4 × 10-5, αp = 1 × 10-4, and αp = 1 × 10-3, Tomohiko model.

Finally, the Kenning's model is seen to be no longer applicable for quite small values ofdp/ltratios.

This brief report provides an overview of the most important physical concepts and experimental data of particle-induced turbulence. One can conclude that the turbulence modulation cannot be fully characterized by a single parameter. The existing criteria such as the length-scale ratio,dp/lt, and the particle momentum number,PaSt, need further experimental/numerical data for full validation and assessment. Several existing physical and theoretical models have been applied to predict turbulence modulation. Among them, the mechanistic model of Kenning is the easiest to implement and provides reasonable results. We believe that this simple model can be reasonably used for the turbulence modulation prediction in large-scale applications of spray systems and that further numerical simulations are required to assess the model.

Acknowledgement

The authors gratefully acknowledge the financial support from Electricité de France (EDF) within the framework of the Generation II & III nuclear reactor research program.