Review on charging model of sand particles due to collisions

Li Xie, Junjie Li, Yakui Liu

College of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China

Key Laboratory of Western Disaster and Environmental Mechanics Attached on Education Ministry of China, Lanzhou University, Lanzhou 730000, China

Keywords:Charging model Sand particles Contact electrification

ABSTRACT In this paper, the models describing the charge transfer between two sand particles due to collisions are reviewed. By comparing the experimental results and the calculated results by the models carried on an individual particle due to a single collision, it indicates the Mosaic model is more reasonable to describe the collision charging mechanism. The Mosaic model cannot only describe the dependence of the collision charges on the relative collision speed and the particle size, but also reveal the relationship between the collision charges with the environmental temperature, the relative humidity and the material parameters, e.g., the absorption energy. Based on the Mosaic model, the model to describe the charges transfer due to multiple collisions is also developed, which can be used to calculate the charges carried by sand particles due to multiple collisions in the wind blown sand flux.

©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

In Baddeley's paper, he wrote that he had the pleasure of observing the electric fluid passing from one wire to anther during the passage of a small dust-storm, at Labor in 1847 [1]. It might be the earliest work to study the electricity happened in dust/sand storm. The studies indicate that the moving sand particles can carry some charges, and when the sand particles carrying net charges are in the air, an electrostatic field can be generated, which is called Aeolian electric field. Since then on,Baddeley [2] did many works to investigate how the electric current generated, usually onward, during the passage of a dust storm, and he found that whirlwinds appear to be composed of a number of electrically charged spiral threads. To some extent,these works promote the wind-sand electrification study, including that how much the amount and what polarity of the net charges carried by the sand particles [3-15]; what affects the amount/polarity of the net charges carried by sand particles[11-13, 15, 16]; how strong the Aeolian electric field generated is during the sand/dust storm [11, 13-15, 17-27]. All the works to answer these questions are boomed out at same time. One of the earliest studies on the polarity of the sand particles by Phillips [8]indicated that sands are prone to make the potential increase after sliding down from a tin plate, a paper plate and a wooden plate. In 1913, Rudge [11] had observed the atmosphere electric field in south Africa, and the atmosphere electric field was recorded by a Bendrof recording electrometer during a sand/dust storm passaging. The results showed that an extraordinary variations of the atmospheric electric field are caused by the presence of dust in the atmosphere, and the atmosphere electric field can reach the value of 5-10 kV/m when the dust is thick.Later Kamra et al. [20, 23-25] studied the characteristics of the electrification in dust storms in field at different places in the southwestern United States, and the wind speed, size distribution of dust particles, atmospheric temperature and relative humidity are also measured to investigate the effect of these factors on the electrification in dust storms. Up to now, there have been so many studies on the wind-sand electrification conducted out,and many results have been achieved. It was found that the polarity of charges carried by sand is not only related to particle size [11-16], but related to the particle size distribution [13, 16],e.g., Greeley and Leach [12] observed that the particles with size larger than 60 μm carry positive charges in a wind tunnel, and vice verse, while Zheng et al. [13] observed that the sand particles higher than 500 μm in particle diameter carry positive charges, but the sand particles less than 250 μm in diameter carry negative charges. The Aeolian electric field in wind sand flux is investigated both in field [14] and in wind tunnels [13, 15],and it was found that the Aeolian electric field is upward and exponentially decreases with the height away from the sand bed in field, which is also related to the particle size and the wind speed[13-15], and the Aeolian electric field generated by mixed sand particles is much stronger than the one by uniform sand particles [13].

Because of the net charges carried by the moving sand particles and the Aeolian electric field generated, an electrostatic force will act on a charged sand particle in the wind blown sand flux/storm. Therefore the trajectories of the sand particles will be changed compared to the ones of neutral particles, and the transport rate of sand particles is also changed such that the characteristic height of saltationz50(the height below which 50%of the mass transport occurs) simulated including the wind-sand electrification approaches to the measurement results [28]. The studies indicate that the threshold speed is much reduced due to the electrostatic force acted on the charged sand particles positioned into an electric container [29-31]. In addition, as rapid development of the wireless technology, many electromagnetic waves (EMWs) need to propagate through a dust/sand environment. Due to the scattering and absorption of EMWs by dust/sand particles, the electromagnetic (EM) signal qualities must be affected, such that the cross-talk is occurred [32, 33]. In 1883, Haddad et al. [34] measured the specific attenuation of EMW with a frequency 9.35 GHz propagating through a mimic sand storm, and they found that the measurement value is much higher than the predicted one. This clear discrepancy between the measurement value and the theory is resolved by Zhou et al.[35]. They firstly proposed a scattering model by considering the contribution of the net charges carried by sand particles, which make the specific attenuation significant increase to approach the measurement.

To sum up, the charges carried by sand particles moving in air will not only reduce the threshold wind speed of sand particles, and change the trajectories and the transport rate of sand particles, but also strengthen the attenuation of EMWs' signal when the EMWs propagate through the dust/sand flux/storm. In order to reveal the effect of charges and Aeolian electric field mentioned above on the wind-sand transportation and the attenuation of the EMWs, it is necessary to clear the mechanism of charge generation of sand particles, including how to be charged of a sand particle, and what kind of the charges carried by the sand particles, and how much amount of charges carried by a sand particle, and what affects the amount of charges carried by a sand particle.

There are many works to reveal the charging mechanism of sand particles. In 1994, Kanagy et al. [36] summarized all reviewed electrical properties of some kinds of sand and inferred 7 potential mechanisms for non-uniform charging of sand grains,including (1) polarization by Earth's atmospheric electric field,(2) triboelectrification, (3) contact electrification, (4) cleavage/fractoelectrification, (5) radiation (X-rays, gamma rays, UV and visible) and charged particle bombardment electrification,(6) pyroelectrification and (7) piezoelectrification. Many researchers infer that the collisions/impacts between the sand particles play an important role in charging mechanism [28, 37,38]. Because of the sand/dust particles being tiny, it is difficult to measure the charges carried by an individual particle. Considering the main constituents of sand particles is SiO2, recently the charges carried by soda-lime glass under 5 charging mechanisms mentioned above are experimentally investigated, except radiation and charged bombardment electrification, and polarization by atmospheric field, shown as in Table 1. From the experimental results in Table 1, it can be found that the surface charge density due to collision between particles and the rubbing between particle and plate are significantly higher than the ones due to other charging mechanism. We infer that the collision and rubbing between particles mainly cause the sand particles to carry some net charges, because the main constituent of the sand particles is also SiO2.

In addition, in 1913, Rudge found that the polarity of the charges carried by sand particles is size-dependence, and usually the larger sand particles carry positive charges, while the smaller sands carry negative charges [11], which is validated by the experiments [12, 13]. Many studies on the Aeolian electric field indicate that the relative humidity [26, 27], the environmental temperature [23], and the wind speed [13, 14, 24] affect the amount of the charges carried by the sand particles.

On basis of these, the studies on building mathematic model to describe the amount of charges carried by an individual sand particle are conducted out, and there are several models are established in recent 20 years, such as effective contact potential difference model [37], high energy state transferred model [39],high-energy hole model [40], H+transferred model [41, 42] and mosaic model [16, 43-45]. In this paper, we reviewed most of the models.

Two solid objects are brought into contact and then separated, and the net charges will be carried on the contact surfaces.If the materials of two objects are different, it is thought that the charges can be transferred between two contact surfaces due to the difference of the work functions of the materials, whateverthe metal or the insulator [46, 47]. For sand particles, one usually thinks that the material is same in statistics, therefore many other factors are considered to develop the charging mechanism of sand particles, such as the contact area difference between two particles [40] or particle size difference [37], or inductive charging of isolated particles in electric field [48]. Next we will introduce each model.

Table 1 Magnitude of surface charge density (σ) in different particle charging mechanism

I Effective contact potential difference model

In 2008, Kok and Renno [28] simulated the electrostatics in wind-blown sand flux, in which the charging process of each sand particle due to collision among particles during saltation is considered. For any two sand particles named asSandLwith radiusRSandRL, they contact with each other shown as in Fig. 1a.Two particles are not equal in size, and assume thatRS＜RL. The net charges carried by both the particles after a single collision are

whereqIandqstand for the charges carried by particles after the collision and before the collision, and the subscripts “S” and “L”stand for the smaller particle and the larger particle.C1andC2are functions of the mutual capacitances of the two particles as defined by Eqs. (5)-(10) of Ref. [49]. ΔΦis an effective contact potential difference between particle pairs of similar composition but different size. That is ΔΦ=B(RL-RS)/(RL+RS). By comparison of the measured electric field and the simulated electric field, they found thatB= (6±4) V [28].

The physically based numerical saltation model that includes the effect of sand electrification is used to simulate the sand transportation, and the results showed that the sand electrification plays an important role in saltation [28]. They found that the sand electrification can resolve the discrepancies existed between the classical saltation theory and field measurements [28].

II High-energy electron transfer model

Lowell and Truscott [48] think that there exist high-energy electrons trapped in defect states, which cannot equilibrate with nearby electrons in low-energy empty on the same particle. Because the particle size is asymmetric, Kok and Lacks [37] further proposed that the more electrons tunnel from the larger particle to the smaller particle than vice versa. They assume that two particles collide at one point, and the high-energy electrons on one particle can relax to the low-energy states on the opposite particles within a distanceδ0between two particle surfaces around the collision point shown as in Fig. 1a.

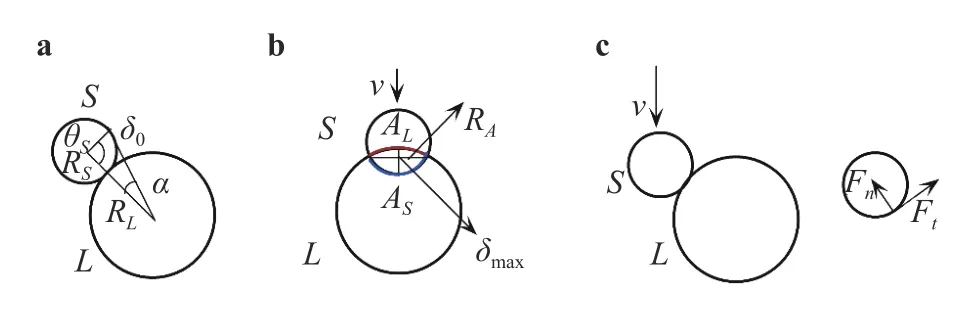
Fig. 1. Schematic of two sand particles colliding. RS and RL are the radii of the smaller particle and the larger particle; δ0 is the distance between two particles, within which the electrons can be transferred from one particle surface to the opposite; v is the relative collision speed; RA is the maximum radius of the compress surface; Fn and Ft are the normal force and the tangential force.

Assume that the initial density of the high-energy states isρH0, to be equal for two particles. The number of the high energy electrons transferred from the smaller particle to the larger particlecan be calculated by

whereθSis the maximum angle from the contact point for which the surface of particleSis within the distanceδ0of the surface of particleL. According to the geometric consideration, shown as in Fig.1a, it has

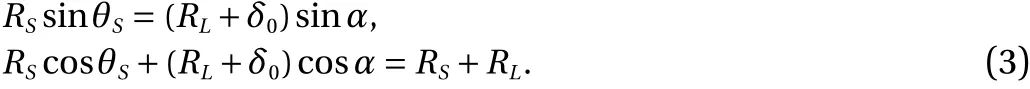
Solving for cosθS, it can be obtained

Substitute Eq. (4) into Eq. (2), the number of the high-energy electrons transferred from the smaller particleSto the larger particleLis

In the similar way, the number of the high-energy electrons transferred from the larger particleLto the smaller particleS,is

The net number of electrons transferred to the smaller particleSisThe net charges carried by the smaller particle,qSII, is

in whicheis the elementary charge of an electron, equal to-1.6×10-19where ℏ is the reduced Planck constant ( ℏ=3.318/π×10-34J·s);mis the electron mass;tcollis the time scale of the collision;ais the radius of potential well corresponding to the electron trap;Ebis the height of the energy barrier between potential wells. In Ref. [37], all these parameters are discussed. They also derived the charges carried by the particles undergoing multiple collisions.According to the charge conservation, the charges carried by the larger particle,

The charging model is applied to predict the surface charge density of sand particles in the dust storms and dust devils, which is in quantitative agreement with the measurements [37].

III High-energy hole model

When two particles collide, a change in shape can be caused due to a load applied to the contact surfaces, but not a point,shown as in Fig. 1b. The areas of the contact surfaces are dependent on the particle material and the relative collision speed.When the relative collision speed is high, a plastic deformation might be occurred in the contact surfaces of particles. As assumed that the charges can be transferred between two surfaces with a distance withinδ0[37], therefore the charges in the contact surfaces can be transferred. In addition, an experiment by Lowell and Truscott showed that the charges due to asymmetric rubbing depend on the total distance of one object rubbed over the other [48]. Therefore, it was inferred that, to study the electrification due to a single collision, the areas of the contact surfaces of the particles should be calculated during collision. Considering two spherical sand particles collide with each other, the areas of the contact surfaces involved into collision are named asALandASfor the larger particle and the smaller particle shown as in Fig. 1b. Assume the charges in the contact surfaces transferred equally from one surface to the opposite surface, and Hu et al. proposed a charging model [40] to calculate the net charges carried by the smaller particle after a single collision as

in whichρ0is the surface charge density. When the elastic collision dynamic process is applied,ASandALcan be calculated by

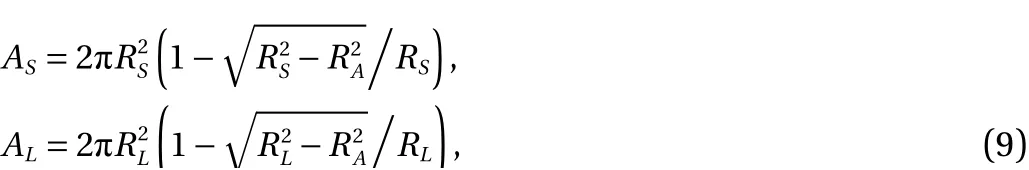
in which, the contact radiuswhereδmaxis the maximum compress. When the relative collision velocity is high, during collision, the compressive stress in some region is high to make the materials have the plastic deformation. For the given material, the upper limit of the compressive stressσmaxcan be simplified to the solution of a flat rigid punch problem, and σmax=(1+π/2)σy, in whichσyis the yield stress of the materials [40]. Usually, when the contact stress exceedsσmax, the plastic deformation occurs. The maximum compressive force happened in the contact surface center, and it is 1.5Fn/(πRA2). Any collision model such as Thorton model applied [50], the compressive force Fncan be calculated. When no charges transferred between the plastic-deformation regions is assumed, the areas of contact surfaces where the charges can be transferred for the smaller and the larger sand particles are equal toin whichRSPandRLPare maximum radius of the region with plastic deformation occurred, and determined by the particle size and the relative collision velocity.

Given the sand particle size and relative collision velocity,the net charges carried by sand particles due to a single collision can be calculated by Eq. (8). The charging model is applied to calculate the charges carried by the glass beads hit by the other glass bead identical in the chemistry. It was found that only if the positive charges transferred between the collision surfaces, the larger particle can be positively electrified [40]. That means when the charges transferred are considered as electrons, the smaller particle will be positively electrified while the larger particle will be negatively electrified. It is inconsistent with the experimental results as that smaller particles carry negative charges while larger particles carry positive charges [40]. Based on X-ray and neutron diffraction studies, there are many defect centers (holes) appearing in the glassy silica and quartz [51]. In sand and dust granular systems, SiO2is the primary chemical composition of sand particles [52-54]. Therefore the hole can be regard as the charge species in sand and dust electrification,such as wind-blown sand/dust storms. Therefore, it was inferred that the transferred charges between the contact surfaces are considered as holes in this charging model.

IV H+ transferred model alerted by temperature difference

In the case of snow/ice, a charging mechanism is proposed by Latham and Mason [55-60], and they thought the temperature difference between two objects resulted in the charges transferred between the contact surfaces. Because the concentrations of H+and OH-go increasing with the increase of the temperature, and the mobility of H+is much faster than the one of OHdue to the mass difference, the more H+transferred along the temperature difference makes the particles electrified after separation. Latham [55] thought it is highly probable that the smaller sand particle is hotter than the larger particle due to the asymmetric rubbing to understand why the sand particles can be electrified. Water content is universal in granular system, and usually a water film can be formed around a sand particle [41].Following Latham's idea, a charging model for sand particles is proposed considering the H+transferred by Gu et al. [41] and Lei et al. [42]. The spherical sand particle oblique collides with another one shown as in Fig. 1c. During the collision, the friction work and some normal compressive energy,Wfmake the internal energy of the sand particle increase. Assuming the conversion efficiency ofWfto the internal energy beafand the internal energy equally partitioned between the two particles, the changes in temperatures of the smaller particle and the larger particles are

where ΔTW,mandchare the temperature change, the mass and the specific heat capacity of the sand particles.

The dynamic collision process is applied, thenWfcan be calculated as following,

in whichεis the restitution coefficient of the sands; Ffand vfare the friction force and the relative speed of one particle sliding over the other along the friction force; Fnand vnare the normal compressive force and the compressive speed.

Usually, a part of the particles' heat energy might be dissipated into the air to make the particles' temperature further reduced during the free movement. Such energy dissipation is related to the area of the particle surface and the contact time with air. Gu et al. [41] and Lei et al. [42] proposed two dissipation models, according to which the changes in particles' temperature are

and

whereψhis the dissipation coefficient,SS/SLandvare the area of the particle surface and the particle's speed;Cis a coefficient related to many constants such as the heat conductivity,Reynolds number and Prandtl number to see Ref. [41] for details.tis the contact time during the collision.

Thus the temperature difference between the smaller particle and the larger particle is

In addition, when there is a potential difference, E, between two particles, which also causes to the charges transfer from one contact surface to the other. The H+flux,J, between the smaller particle and the larger particle is directly proportional to the potential difference and the temperature difference as follows,

in whichαis a coefficient related to the relative humidity [41],andβis a coefficient related to the relative humidity and the ionic product of water [41, 42]. Therefore, the net charges on the smaller sand particle would be produced as

According to the charge conservation, the net charges carried by the larger sand particle

This model is applied into the numerical simulation of the wind sand electrification in the wind sand flux, and it was found that the simulated charge-to-mass of sands and the electric field in wind tunnel agree well with the experimental results [41, 42].

V Mosaic model

In 1931, Mattson [61, 62] attributed the colloidal behavior of soil particle to high surface charges. As a kind of soil, the dry sand particles usually carry net surface charges as a result of substitution of metal ions in the lattice, such as isomorphous replacement of the Si4+by a AL3+in an array of solid SiO2tetrahedron [63, 64]. In addition, the dissociation of functional groups[63] and dangling bonds on the sand surface [65], also make the permanent charges and variable charges developed on the dry sand particle surface. As mentioned above, in nature, sand particles are hydrophilic and have thin layers of water molecules on their surfaces and an electric double layer forms on the sand surface shown as in Fig. 2a, and the net charges on the surface of sand particles would be balanced by the counter ions in the water layer [66, 67] to make them electrically neutral.

Apodaca et al. [68] found that two polydimethylsiloxane(PDMS) plates with the same area could be charged after they contacted on the surfaces. Based on this observation, they proposed that two types of electrical potential centers exist on the PDMS's surface, which could be respectively named charge donor and acceptor and were separated by each other, like a Mosaic pattern. For sand particles, when two solid surfaces with electric double layer are brought into contact, the surface electric double layers will also be brought into contact [69, 70]. In the case of collision contact, contact force acting upon the contact surfaces of two particles could distort the electric double layers.The diffuse layer is like liquid and is easily squeezed aside due to collision, while the stern layer sticks to the solid surface firmly.Therefore, the stern layers on the two spheres' surfaces will be involved in collision contact process [69]. Including counter ions in the stern layer and original surface patches of spheres, there are two kinds of surface sites brought into contact as shown in Fig. 2b. The counter ions adsorbed on one surface transfer to the other surface, and they can be regarded as donors as presented in Ref. [39]. Because the distributions of counter ions and original surface patches could be different on the two contact surfaces,the counter ion transfer occurs when one counter-ion site of one surface meets the original sites (named acceptors) on the other surface during the collision.

The mean number of counter ions transferred from one contacting surface to the other can be calculated to refer to Ref. [44],which are not equal because of the difference in contacting areas that are brought into contact during collision of the two particles. According to Refs. [44, 45], the net number of counter ions (donors) transferred to the particleL, ΔN, between two surfaces of the particlesSandLcan be calculated by the following expression,

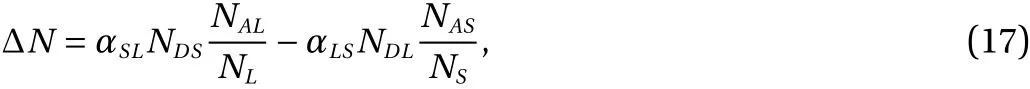
whereNDSandNASare respectively the number of donors and acceptors on the contacting area of particleS, andNDLandNALare respectively the numbers of donors and acceptors on contacting area of particleL. LetNSandNLdenote the total number of sites that are possible to give or accept charges on the contacting areas of particleSandL, respectively, that meansNS=NDS+NASandNL=NDL+NAL.αijstands for the probability that a charge be transferred from surfaceito surfacej(i,j=S,L),which depends on the energy difference between the donors and acceptors and ambient temperature. Because the two contacting particles are of identical material, we assume that,αSL=αLS=1 to see Ref. [44].

Fig. 2. Schematic of a electric double layers on the sand surface, including stern layer and diffuse layer and b charge site distribution on the sand surface

Baytekin et al. [45] pointed out that both the number of donors and acceptors are stochastic variables and obey the binomial distribution. Therefore, the number of the net charges from contact surface of particleSto that of particleLis also a stochastic variable, the mean value of which can be obtained by taking average on both sides of Eq. (17), i.e.

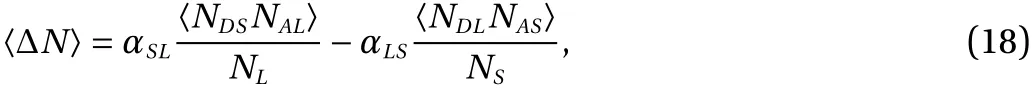
in which 〈·〉 takes average of a variable. Usually, the number of donors on surfaceSis independent on the number of the acceptors on surfaceL. Assume the probability of donors appears on the surfaceSand surfaceLarePDSandPDL,respectively. Thus,〈NDSNAL〉=〈NDS〉〈NAL〉=PDSNSNL(1-PDL)and 〈NDLNAS〉=〈NDL〉〈NAS〉=PDLNSNL(1-PDS). According to the two-phase equilibrium model presented by Hogue et al. [67, 70]for neutral particle before collision, the number of counter ions,i.e. the number of donors, can be calculated as following,

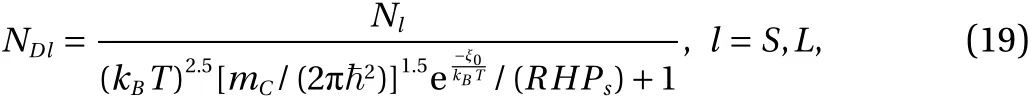
in whichkBis Boltzmann's constant (kB=1.38×10-23J·K-1), andTdenotes ambient temperature in K;mCis the mass of a charge;RHis the relative humidity, and 0 ＜RH＜ 1;Psdenotes the saturated vapor pressure;ξ0is the adsorption energy of the sands. Therefore,

which means

Because the two particles are of identical material, assume that the number densityncof donor sites on the two contacting surfaces are equal andPD=PDS=PDL. Therefore,NS=ncASandNL=ncAL. Therefore, the mean value of the net number of transferred donors is 〈 ΔN〉=ncPD(1-PD)(AS-AL), from which the net charges,carried by the smaller particle after the collision between these two particles is,

Here, according to Langmuir isotherm [71], it is assumed that one site can only adsorb one ion carrying one elementary charge,qc=1.6×10-19C. Lee and Pantano [65] found there were 7.2 dangling bonds per square nanometer on fracture surface of glass. Because dangling bonds are possible to form donors or acceptors, we assume the number densityncin Eq. (21) be of the same order as that of dangling bonds, i.e.nc=1.0×1018m-2. For the given particle size and relative collision velocity,ASandALcan be calculated employing the dynamics to see model III, and further the net charges carried by two particles can be calculated by Eq. (21). According to the charge conversation, the charges carried by the larger particle,

It can be found that all these 5 models mentioned above are related to the particle size. The models III-V are also related to the relative collision velocity. The former two models are independent on the relative collision velocity and the relative humidity. The models IV and V are related to the relative humidity as well. In addition, it is clarified that the charges transferred between the contact surfaces are electrons for models I and II,holes for the model III, and H+for the model IV. In the model V,it is not clear what kind of charges is transferred between the contact surfaces, but the results indicate that the polarity of charges carried by the larger particle is the same as the one of the transferred charges. Next, we will calculate the charges carried by the larger particle applying these five models due to a single collision, for the neutral particles before collisions, and the change of the charges in the radius ratio, the relative collision speed and the relative humidity shown as in Fig. 3.

From Fig. 3a, it can be found that net charges carried by an individual sand particle due to a single collision are not equal in quantity calculated by different charging model, and the trend of charges in particle radius ratioRS/RLis not same. The net charges calculated by models II and IV decrease asRS/RLincreasing, while the charges calculated by models I, III and V go up and then decrease asRS/RLincreasing, and there is peak value in the charge-(RS/RL) curve, which is also observed in experiments [40, 44]. The charges carried by an individual sand particle due to a single collision increase as the collision speed increases calculated by the models III-V to see Fig. 3b. Only models IV and V are related toRH, but the dependence of the model IV onRHis implicated in parametersαandβ, which cannot be identified. The charges calculated by the model V in change ofRHare shown as in Fig. 3c, from which it can be found that the charges-RHdependence is related to the surface absorption energy. As the different absorption energy given, there exist three different situations of the charge-RH, which all have been observed in the experiments [43, 72].

Zheng et al. [73] pointed out that theRHnot only affected the Aeolian electric field, but also affected the charge transfer between sand particles when they collided with each other. Furthermore, by counting in the effect ofRHon the energy barrier in model II, they found that with increasingRH, the amount of charges transferred between two particles during colliding reached a maximum at some value ofRH, then decreased rapidly with further increase of RH, as mentioned in Fig. 3c. And they also found this dependence of the amount of transferred charges depended on the initial energy barrier [73]. This model also revealed that the charge transfer was affected by water layer compression during the colliding process.

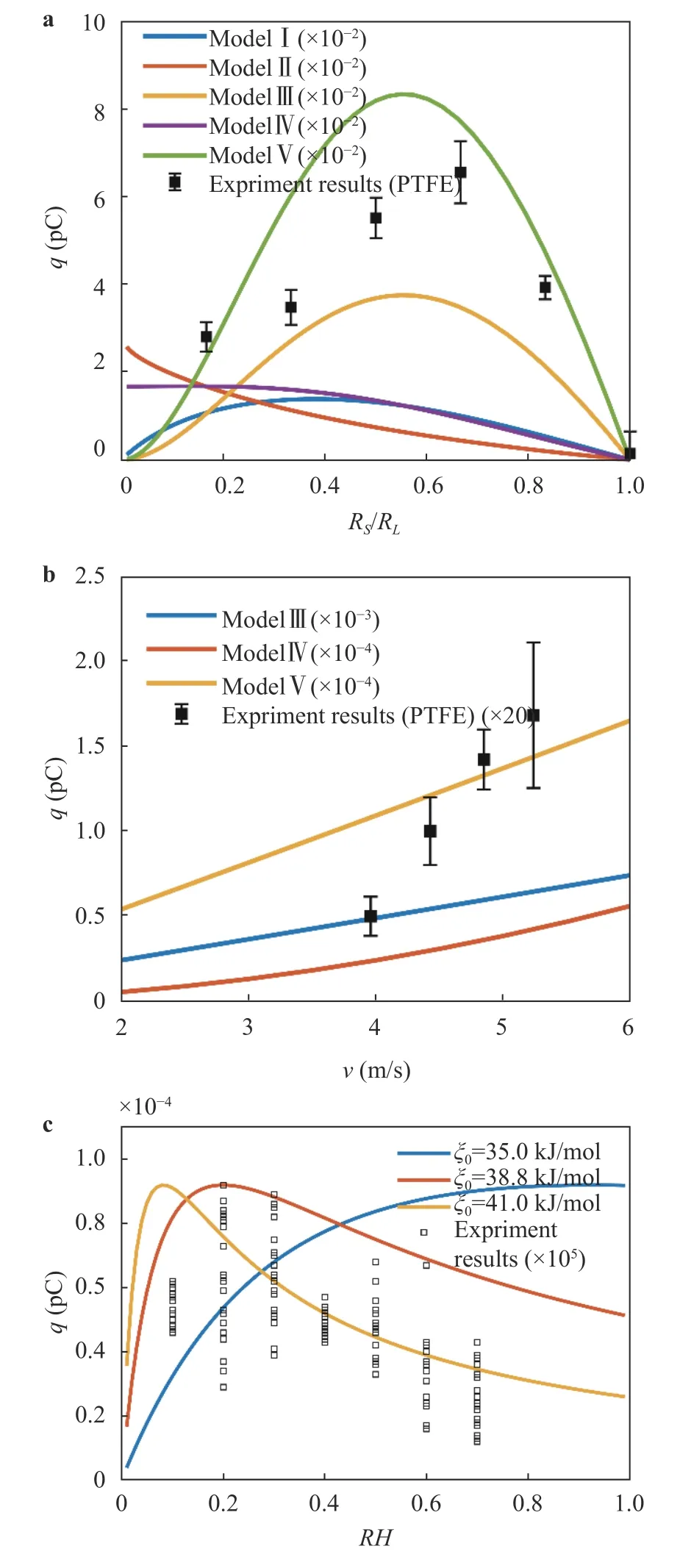
Fig. 3. Net charges carried by the larger sand particle due to a single collision, versus a particle radius ratio, b collision speed and c relative humidity. In a, v=3.0 m/s, RH=0.4 and RL=0.4 mm. B=2 V is used in model I. a=1 Å , Eb=4.5 eV and ρH0=1×1018 m-2 are used in model II.ρ0=0.16 C/m2 is used in model III.αfβe-CS t=αfβe-CLt=7.2×10-15 is used in model IV. nc=1×1018 m-2 and ξ0=38.8 kJ/mol are used in model V. In b, RH=0.2, RS=0.2 mm and RL=0.4 mm. The others parameters used in models III-IV are same as ones used in a. In c, v=3 m/s, RS=0.2 mm, RL=0.4 mm, nc=1×1018 m-2, and T=298 K. The experimental results are shown as solid square, v=3.96 m/s, RL=6 mm,poly tetra fluoro ethylene (PTFE) sphere in a, RS=4 mm, RL=10 mm,PTFE sphere in b, and v=3.13 m/s, Rs=5 mm, RL=10 mm, soda-lime glass sphere in c.

Let's look back to see the mathematic expressions of the model III and the model V, and it can be found that the charges carried by a particle calculated by these model are proportional to the area difference between the contact surfaces involved into the collision. Although the model IV is not directly related to the area difference, the similar dynamics collision process is applied. The area difference is dependent on the relative collision velocity, the particle size and the particle size ratio, based on which the maximum compress stress and strain can be determined. Usually, the higher the relative collision velocity, the larger the strain difference is for the given particles. As Ref. [74], when two objects are brought into contact, the contact surfaces become deformed, which changes the chemical properties of the surfaces [75]. Because of the difference in the deformations of the two contacting surfaces, the changes in the chemical properties of the two contacting surfaces will be different, creating a driving force for a net transfer of charges from one surface to the other. Therefore, the net charges transferred is proportional to the area difference. And it also reveals why the amount of the net charges is related to the relative collision speed, the particle size and the size ratio. The rest parameters except the area difference in the mathematical expressions of the models imply what kind of the charge is transferred, and the relationship of the net charges with the environmental temperature, the relative humidity and the particle material absorption energy. Now the results shown as in Fig. 3 indicate that the model V can describe the relationship of the net charges with the relative collision velocity,the particle size, the relative humidity, the environmental temperature and the material parameters, which is also validated by experimental results. The all results shown in Fig. 3 calculated by the model V, we assume that the transferred charges are H+. But no direct experiment or study indicates that what kind of the transferred charges in model V is. For the model V itself, it doesn't confine the charges transferred which can be electrons,any irons or material patches.

In the wind sand flux, there are frequent collisions happened between the sand particles. One particle will experience many collisions with the other in the air and in the sand bed. The model V can be extended to derive the charges carried by a sand particle after experiencing multiple collisions. Next, we will brief the net charges carried by the particle due to multiple collisions.

Assume that particleSfirst collide with particlek(k=1, 2, …,N,k≠S) to see Fig. 4a. Before the collision, the distribution of donors on the particle surfaces are identical in statistics, as shown in Fig. 4b. It is clear that a single collision between any two particles only occurs within a very limited particle surface,and not the whole particle surface. Therefore, a single collision only changes the distribution of the charge site, such as donor,in a very limited area, as shown in Fig. 4c. However, when multiple collisions are occurred between particles, or a given particle collides with other particles, the collision contact surface will be randomly distributed over the particle surface. Consequently, it becomes very difficult to determine the donor distribution. Here,for simplicity, we assume that the donors are evenly redistributed after each collision and the probability of donor is the same anywhere on the entire surface of the particle as shown in Fig. 4d.Assume before colliding with particleL, particleShas encountering (n-1) collisions and (mL-1) collisions for particleL. According to the conservation of the donor number, the probabilities of donors on particleS,PDS(n), and particleL,PDL(mL), aftern-th collision for the particleSandmL-th collision for the particleL, are

Fig. 4. a N particle system; b the charge size distribution before first collision; c the charge site distribution of the collision surfaces after collision; d the charge site redistributed

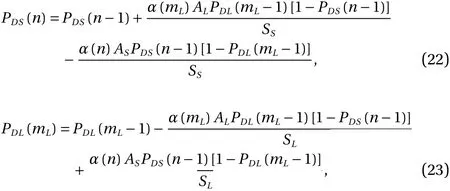
in which,sS=4πRS2andsL=4πRL2. Any particle that has not collided with others, are electrically neutral. Therefore, we can assume thatPDS(0)=PDL(0)=PD, substitute which into Eqs. (22)and (23), the probability of donors on the particleS,PDS(n), and the probability of the donors on the particleL,PDL(mL) can be calculated. Thus, by substituting Eqs. (22) and (23) into Eq. (18),when the particle size, the relative collision velocity and particle material are known, the net charges transferred to the particleScan be calculated as follows, to refer to Ref. [16] for details.

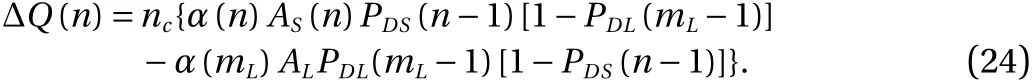
The total net charge carried by the particleSparticle due toncollisions can be calculated by summing the net charges transferred to the particleSafter each collision, and that is

It is noteworthy that when the particles carry net charges before collision, the effect of the electric field onPDS(n) andPDL(mL) needs to be considered as ones given in Ref. [70].

Thus Eq. (25) can be used into the wind sand flux simulation to calculate the charges carried by sand particles due to the multiple collisions. For simplicity, the charges carried by two particles due to repeat collisions are shown as in Fig. 5, from which it can be found that net charges carried by smaller particle and larger particle increase as the collision time increases, and a saturation charges can be achieved finally.α(·) is an important parameter to determine the saturation charges, but there is no study onα(·). As the net charges are getting more on each particle, the transfer probability of a donor should become low,so the charge-dependenceα(·) is chosen in this paper to calculate the net charges carried by an individual particle, that α(n)=[ΔQ(n-1)/Q(n-1)]0.0001n, in which ΔQ(n-1) andQ(n-1)are the net charges transferred for the (n-1)-th collision and the total net charges carried by the particle after the (n-1)-th collision. We hope the further work on simulating the Aeolian electric field in the sand flux by using this charging model. And the dependence of the charge-mass ratio and the Aeolian electric field on the some parameters such as the particle size, the relative humidity can be also analyzed.

Fig. 5. Net charges carried by small particle and large particle due to repeat collision calculated by model V. n is the collision number.T=298 K. v=3 m/s. RH=0.4. RS=0.2 mm and RL=0.4 mm. nc=1×1018 m-2 and ξ0=38.8 kJ/mol.

The models describing the amount of charges carried by sand particles due to a single collision are reviewed. We found that the Mosaic model cannot only describe the dependence of the collision charges on the relative collision speed and the particle size, but also reveal the relationship between the collision charges with the environmental temperature, the relative humidity and the material parameters, e.g., the absorption energy. Based on the Mosaic model, the model to describe the charges transfer due to multiple collisions is also developed,which can be used to calculate the charges carried by sand particles due to multiple collisions in the wind blown sand flux.

There are many other granular systems, such as the drifting snow particles [76, 77], the particle flow in pipelines [78], where frequent particle collisions are involved during the particle transportation. Due to the electrostatic forces acting on charged particles, the dynamics of particle systems could be changed significantly. For example, the Aeolian saltation would be enhanced because of the cohesion between particles [76], and pipelines might be blocked due to the aggregation of powders on the wall of pipes [78]. The models mentioned above are important for revealing the effect of electrostatic forces on the dynamics of particle systems.

Acknowledgement

We are grateful to the National Natural Science Foundation of China (Grants 51435008, 11472122 and 11272139).