导数定义课堂教学的设计与实践

杨德志

（辽东学院师范学院 辽宁丹东 118000）

思考：你会求平均速度吗？

例：甲乙两地之间的距离为200公里，一汽车从甲地到乙地行驶了4小时，请你计算该汽车的平均速度是多少？

学生：平均速度为：200÷4=50（公里/小时）

思考：平均速度能代表瞬时速度吗？

学生：平均速度50公里/小时不能代表某一时刻的瞬时速度，该汽车不一定是匀速行驶的，可能时快时慢，也可能中途停车。

思考：你会求第二个小时内的平均速度吗？

思考：高中时，我们学过通过已知两点去求曲线的斜率。你能求出下图这条割线的斜率吗？

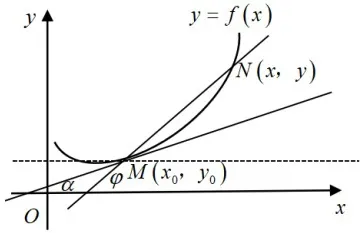
图1 切线斜率图

思考：你知道割线斜率与切线斜率的关系吗？

为了让学生感性认识割线转动到切线的过程，笔者借助大学数学工具箱来演示这一变化过程。

思考：在这一变化过程中，k割与k切有什么关系吗？

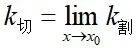
思考：通过上面两个实例你发现了什么？

学生：一个物理上的瞬时速度问题，一个是几何问题切线斜率问题。

思考：抛开物理和几何的应用背景，这两个问题有什么共性？

学生：增量之比的极限。

思考：从数学结构上，其都是研究变化率的极限问题。因此，我们可按照作差、作比值、求极限这三个步骤来概括这类问题！

你能用作差、作比值、求极限这三个步骤来刻画一下这类问题吗？

学生：这三个步骤可概括为：

（1）在x0处给自变量一个改变量：

导数定义在微积分课程中的重要性是不言而喻的，是它开始了微积分的篇章，是它开始使用极限为工具来研究变化率的问题。因此，它是微分学的基石，它是积分学的逆运算，它是高等数学的核心内容。