提高几何直观能力有“四招”
2020-08-06纪金禀
纪金禀

摘 要:几何直观不仅是一种解决问题的方法,还是一种能力。几何直观基于直观感知过程,离不开理性思考。教学中,可以结合学生感知过程的特点、思维的特点,通过引导学生“看”“操作”“想象”“说”,使观察更深刻,思考更深入,从而提高学生的几何直观能力。
关键词:几何直观能力;感知;理性思考
一方面,几何直观是指,借助于见到的(或想象出来的)几何图形的形象关系,对数学的研究对象(空间形式和数量关系)进行直接感知、整体把握的能力[1]。通过几何直观获得的感性认识,能让学生在头脑中产生某种关系,并联系实际问题,使数学问题得到解决。不仅如此,几何直观被认为是一种能力。另一方面,几何直观是在直观感知的感性基础之上所形成的理性思考[2]。可见,几何直观是一种基于感性认识并伴随理性思考的能力。
因此,提高几何直观能力,不仅要从感知过程入手,还应重视理性思考过程,使感知更准确、有效,使思考更清晰、深入。有目的地观察能使感知更准确,操作和想象能在脑海中对图形进行再加工,说理能对感性材料进行更深层次的理性思考。教学中要让学生学会“看”“操作”“想象”和“说”,引导学生达到更高层次的几何直观,提高几何直观能力。
一、学会“看”
几何直观是一种感知活动,对几何图形的感知离不开充分的观察。教学中,存在学生看到几何图形仍无法解决问题的现象,笔者认为在于学生缺乏观察的目的性。观察的漫无目的使学生观察图形时忽略关键因素,造成思维模糊、停滞甚至偏离实际问题。学会有目的地观察,利于学生更快速、更准确地把握几何图形的关键特征,使体验更深刻,理性思考更深入,从而整体把握图形中的某种关系。
【案例1】
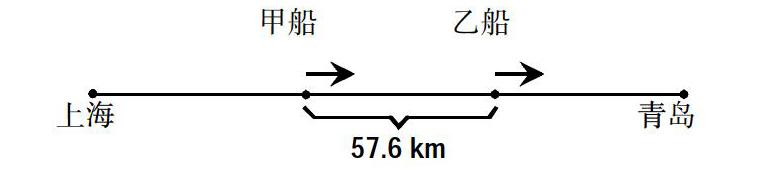
甲、乙两艘轮船同时从上海出发开往青岛。经过18小时后,甲船落后乙船57.6km。甲船每小时行32.5km,乙船每小时行多少千米?(用方程解答)
■
师:从上图中能找出怎样的等量关系呢?
生:甲船落后乙船57.6km。
师:怎么列等量关系呢?
(等待许久,无人回答。)
师:既然甲船落后乙船57.6km。在上图中,甲船和乙船的路程有怎样的关系呢?请你先自己想一想,列出等量关系式,再和四人小组说说你的想法。
生:乙船的路程-甲船的路程=相差的路程
师:还可以怎么列等量关系式?
生:甲船的路程+相差的路程=乙船的路程
由于图中包含运动方向、起始点、相差的路程等信息,学生的第一次观察漫无目的,思路最终转移到图中的数字信息——
57.6km,最终用题干中的“甲船落后乙船57.6km”回答问题,思维停滞不前。第二次引导学生观察两船的路程,学生的思维便集中到图形中,构建起“甲船的路程+相差的路程=乙船的路程”的形象关系。通过让学生有目的地“看”,培养观察的目的性。在往后的学习中,学生能自发地进行有目的的观察和思考,更有效地把握图形中的关系。
二、学会“操作”
学生在动手活动中形成的个体经验是发展几何直观的基础,是感受、理解抽象几何直观的有力支撑[3]。常见的操作活动有:剪、拼、摆、圈、折、量、画等,这些活动不仅要调动视觉感官,还使学生的多种感官协同参与,是一种更全面的感知,对已有图形进行二次加工,使感知更准确。教学中,要让学生感受到操作活动是理解图形的重要方法,更要让操作活动成为在图形启发下的自觉反应,提高几何直观能力。
【案例2】
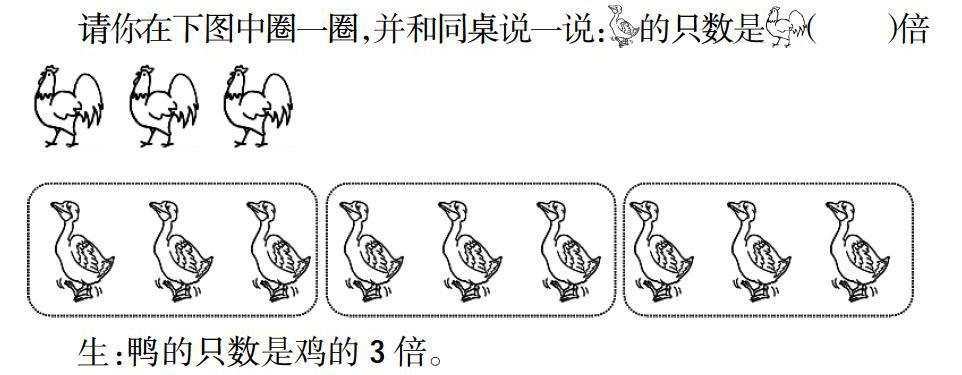
请你在下图中圈一圈,并和同桌说一说:的只数是()倍
生:鸭的只数是鸡的3倍。
师:你是怎么想的?
生:鸡有3只,所以鸭要3只3只地圈,圈三次,有3个3只,所以鸭的只数是鸡的3倍。
师:为什么鸭要3只3只地圈?
生:因为鸡有3只。
师:看来要以鸡的数量为标准来圈呢!那圈三次说明什么呢?
生:圈3次说明有3个3只。
师:你认为把图形圈一圈有什么好处?
生:能更快地看出要以鸡的只数为标准,鸭有3个3只,所以鸭的只数是鸡的3倍。
学生较难从等距排列的鸭子中寻找数量关系,更难理解要以鸡的数量为标准,鸭有3个3只这一本质性关系。通过“圈一圈”这一操作活动,学生能自觉地以鸡的只数为标准,每3只鸭圈一次,使“3个3只”的关系更为突出,发现“圈一圈”能使图形中的关系变得更容易理解。學生感受到操作活动对理解图形关系的积极性,当观察图形遇到困难时,会自觉地对图形进行相关操作,几何直观能力也将得到提高。
三、学会“想象”
几何直观不仅借助平面图形,还借助立体图形;不仅借助静态图形,还借助动态图形;不仅借助单一图形,还借助多个图形甚至无数个图形。因此,在几何直观活动中,时常离不开“想象”。更有研究者指出:发展几何直观,最重要的就是要发展学生的空间想象能力[3]。想象活动有利于突破“二维与三维”“有限与无限”“静态与动态”之间的界限,达到更高层次的几何直观。培养几何直观能力不能局限于观察、操作活动,还要引导学生进行想象。
【案例3】
用小正方体拼成下图中的大正方体后,把它们的表面刷上红色的漆,其中两面涂色的小正方体有多少块?
师:两面涂色的小正方体有几块?
生:这里有两块、还有这里……都是两块(手指着看得的九条棱),一共是18块。
师:想象一下,除了看得到的棱上一共有18块,还有吗?
生:还有后面看不到的这三条棱(手指着那三条棱的大致位置),每条棱上都有2块是2面涂色的。
师:怎么求这些涂色的小正方体有多少块?
生:正方体有12条棱,每条棱上有2块小正方体两面涂色,12×2=24(块)。
学生之所以得出“18个”的错误结论,在于不能将看到的正方体当立体图形看待,没有进行适当的空间想象。通过引导学生想象其余三条棱上小正方体的特点,会发现每条棱上都有2个小正方体是两面涂色的。学生解决问题时不可能每次都拥有实物进行思考,平面呈现的图形结合空间想象是几何直观中常遇到的情况。想象活动有利于思维摆脱二维空间的束缚,在三维空间中有效进行,达到更高层次的几何直观。
四、学会“说”
几何直观基于感性认识,伴有理性思考,但这种思考并不是严密的推理,有时是一闪而过的感悟,或快速而簡单推理的结果,容易出现片面的理解和随意的判断,因此常出现模糊甚至错误的结论。通过“说”的活动,学生能“反刍”对图形的感知过程,边“说”边梳理自己的思路,进行理性层面的深度加工,使感知到的关系变得清晰而确定。“说”具有两方面的意义,一来能深化对图形理解,修正偏差;二来能建立起实际问题和几何图形之间的桥梁,利于解决问题。
(一)在“说”中深化理解
学生对图形的理解有时是模糊甚至是错误的,如果能在大脑中对图形中的关系进行二次加工,进一步思考其中的关系,就有助于形成清晰的认识、修正错误的理解。“说”是一种重要的方法,学生将直观感知到的关系“说”出来,也是在理性层面上梳理感知过程,有利于图形表征与文字表征之间的相互转化,进一步理解图形中的关系,使感知更清晰、更准确。
【案例4】
李伯伯家有一块公顷的地。种土豆的面积占了这块地的,种土豆的面积是多少公顷?
师:结合图形想一想,种土豆的面积是多少公顷?
生:公顷。
师:你是怎么想的?
生:把种土豆的面积平均分成5份,每份就是公顷。
师:看看图,再回想刚才平均分的过程。
生:先把这1公顷平均分成2份,再把其中一份平均分成5份,这样的1份是公顷。
师:仔细回想,刚才你把1公顷平均分了几次?
生:两次。
师:我们把谁看作单位1呢?
生:(学生沉思片刻)应该是公顷,刚才把1公顷看作单位1,平均分成2份后,再把其中的一份平均分成5份,相当于把1公顷平均分成10份,所以是公顷。
通过不断引导学生观察图,回想原本的思考过程,“说”出对图形的理解,学生逐渐理解应把1公顷看作单位1,将两次平均分相结合,准确把握每一份与1公顷的关系。学生的“说”是对思考过程的“反刍”,不仅利于教师把握学生的认知过程,也利于学生在“说”中修正错误,在“说”中深化理解。
(二)在“说”中解决问题
学生利用图形分析问题时,问题的解决过程也在图中进行着,而图形是实际问题的抽象表达,与实际问题之间存在一定的差异,容易造成学生画出了图,却无法解决问题的情况。究其原因,在于学生无法将图形所代表的意义与实际问题相联系。可引导学生将图形与实际问题的联系“说”出来,在图形中进行有效的演绎,从而解决问题。
【案例5】
题目:马路一边栽了50棵梧桐树。如果每两棵梧桐树中间载一棵银杏树,一共要栽多少棵银杏树?
(学生画出了图,却无法解决问题)
师:在这个图里,你用什么表示梧桐树和银杏树?
生:这些(指着竖着的长线段)表示梧桐树,银杏树是这一些短的。
师:要求的是什么?
生:银杏树的数量。
师:银杏树种的位置有什么特点?
生:种在两棵梧桐树之间。
师:能种几棵银杏树跟什么有关?
生:(学生兴奋地说到)间隔!一个间隔对应一棵银杏树,有几个间隔,就能种几棵银杏树!
可以看出,学生已经会用线段图表示种树的情况,但是无法将银杏树数量与间隔数相联系,通过引导学生思考图中画出的每个元素与实际问题的联系,而后学生忽然兴奋地说出答案,说明学生已能将问题与图形相结合,感悟到间隔数和银杏树数量的一一对应关系,使线段图和实际问题建立起桥梁,从而解决问题。
总之,几何直观是基于感性认识的理性思考所致,通过“看”“操作”“想象”使学生的感知更深刻,思考更深入,对图形拥有更高层次的理解,通过“说”深化对图形的理解、沟通图形与实际问题之间的联系,使图形的介入真正利于问题的解决。教学中应引导学生学会 “看”“操作”“想象”和“说”,提高学生的几何直观能力。
参考文献:
[1]孔凡哲,史宁中.关于几何直观的含义与表现形式:对《义务教育数学课程标准(2011年版)》的一点认识[J].课程·教材·教法,2012,32(7):92-97.
[2]唐平,付天贵.义务教育阶段几何直观分析框架[J].教学与管理,2016(30):83-85.
[3]郁军,张佩玲.小学数学核心概念教学研究[M].北京:教育科学出版社,2017:62-68.
