以“数三角形”为例谈数学思想方法在小学数学课堂中的有效渗透

李海涛

摘 要：2011版数学新课标中明确了“基本思想”也就是数学思想方法的价值和地位，现今社会创新型人才的需求要求数学思想方法必须从小学数学课堂抓起。具体到数三角形这个课例，课前从数线段、数角入手铺垫，新授从抛出问题找到困难再到探索研究解决问题，最后及时归纳总结，在无形中润物无声地渗透思想方法。拓展环节巧设题目在争论中打破思维定势，课后留疑为以后独立探索掌握思想方法这一神兵利器留有空间。

关键词：数学思想方法;小学数学教学;化繁为简;有序;渗透;真正发生

一、数学思想方法的价值和渗透数学思想方法的必要性

2011版数学新课程标准明确指出：“学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验……”“基本思想”正式成为“四基”之一。将思想方法列入促进学生在义务教育阶段全面发展的目标之一，在理论上明确了其在小学数学教学中的重要价值和关键地位。

布鲁纳指出，掌握基本数学思想和方法能使数学更易于理解和记忆，领会基本数学思想和方法是通向迁移大道的“光明之路”。数学思想，就是对数学事实与理论经过概括后产生的本质认识，是解决数学问题的基本观点和根本思想方法，也就是我们在现在的小学数学教育中所提出的“通法”。它们含有传统数学思想的精华和现代数学思想的基本特征，能够为小学生解决数学问题能力的培养和数学思维的发展起到奠基性作用。在习总书记的倡导和推动下，培养创新型人才已成为社会共识，数学思想方法的培养是培育创新型人才的关键一招，其培养和渗透必须从小学数学课堂开始抓起。

二、“数三角形”课例展示及思想方法渗透分析

教学内容：人教版四年级下册P71练习题7

1.前置探索，承上启下

师：昨天老师给大家布置了“数一数”的前置作业，下面一起来汇报交流一下。

学生汇报自己数线段、数角时用到的方法。

师：刚才数线段时大家想出了两种不同的方法，可以先1条1条地数，再2条2条地数，依次数下去。也可以先固定一个端点，把从这个端点出发的全部数完，再依次数下去，两种方法都是非常“有序”的。数角的时候大家也用到了类似的方法，在“有序”的引领下做到了不重复也不遗漏。

师：大家数线段、数角都学得非常好。接下来你们还想数什么？

生：平行四边形、长方形、正方形、三角形……

师：今天这节课我们先重点来研究数三角形。

导入环节设计了数线段和数角的前置作业，目的是让学生在自主探索中唤起旧知，回忆起三、四年级数图形教学当中“有序”。经历了先前置探究再课上交流这两次思维火花的碰撞，对“有序”的思想方法进行了有效渗透，为数三角形思想方法的进一步渗透做好了铺垫。

2.探究新授，润物无声

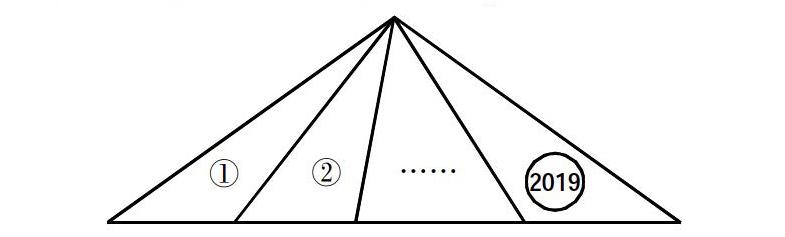
师：图中一共有多少个三角形，开始数吧。

师：你数出来了吗？你遇到了什么困难？

生：数不出来。單个的小三角形有2019个，还有组合起来的三角形，太多了。

师：是呀，单个基本三角形都有2019个，还有2个2个地数，3个3个地数……真的太多了。碰到了这种很复杂的问题，我们要怎样解决呢？

生：要是少一点就好了，就能数出来了。

师：是的，碰到一个复杂的问题，可以先把复杂变简单，从简单入手去研究。听你们的，少一点，少到多少呢？

生：2个基本三角形、3个基本三角形……

师：每个人想要研究的数量不同，为了提高学习效果，小组内分工合作，先定好要研究的基本三角形个数，把三角形画好，再数一数，最后把结果记录下来。

这个环节，首先抛出一个复杂的数学问题让学生独立分析，给学生真正直面问题的机会，面对困难自主开始想方法去解决问题。经历了这样一个让学习真正发生的心路历程，可以更好地激发学生的探索兴趣，引发学生真正思考，提高了后面思想方法渗透环节的可接受性。碰到复杂情况怎么办？这个问题引发学生的大讨论，学生根据生活和学习经验等自然地想到了要变“多”为“少”，把“复杂”变成“简单”，在无形中学生自己提出了解决问题时要“化繁为简”，把数学思想方法在讨论中巧妙地渗透了进去，为以后学生独立解决时唤醒“化繁为简”的思想方法打下了很好的基础，为解决这道题指明了方向。

师：老师巡看时，发现有些同学做得非常好，小组内的同学互相交流一下。

依次请2个基本三角形、3个基本三角形（重点）的同学上来讲怎样数的。

生：先数3个基本三角形，再数由2个基本三角形组成的，再数由3个基本三角形组成的。

师：李老师来当你的助手，你数，我贴。观察一下，李老师为什么要这么摆，你发现了什么？如果我们用算式简单地记录下来，怎么写？

生：这样摆非常有序，可以看出数法。3+2+1=6（个）

师：3个基本三角形的类型，还有不同的数法吗？

生：先固定三角形最左边的边，把含有这条边的三角形全部数出来有3个，再固定第二条边不重复的数有2个，再固定第三条边有1个。

师：两种方法都是3+2+1，这两个3一样吗？这两种方法，又有什么联系的地方呢？

生：不一样，第一个3是三个基本三角形，第二个3是从最左边这条边出发数出来的3个三角形。

生：第一种数法如果竖着摆就是第二种数法，虽然两个3不一样，但数出来结果一样，可以转化一下变得一样。

师：刚刚我们数三角形的时候，想了两种不同的方法。虽然方法不同，但都做到了“有序”思考，成功地解决了问题。而且，大家通过“转化”，使两种方法又联系起来，把“变与不变”分得清清楚楚。

在学生数三角形的时候，抓住3个基本三角形这种类型，让学生讲了自己的两种不同方法，殊途同归，再次凸显“有序”思想方法的价值和普遍适用性，加深学生的认识。两个“3”一样吗，又有什么联系，这一关键问题引发学生仔细地观察和思考，在问题的引导下，学生通过观察发现两者换个方向看可以变得一样，渗透了“转化”的思想。同时，本来不一样又回到一样，经历了这个变化过程，在比较中渗透了“变与不变”的数学思想。数学思想方法的渗透需要有效的载体，选择合理的数学问题可以在同一问题情境下渗透多种数学思想。

师：5个基本三角形的类型，猜一猜，一共有多少个三角形？怎么想的？

生：5+4+3+2+1。根据前面发现了规律，一共几个基本三角形就从几往下一直加到1。

师生一起来验证5个、6个、7个基本三角形的类型。

师：那10个基本三角形的、200个基本三角形的，2019个呢？n个呢？

生：2019+2018+…+2+1。n+（n-1）+……+2+1。

师：这个复杂的问题被我们解决了，我们是怎样把它解决出来的呢？

生：我们碰到了一个复杂的数学问题，把多变成少，从简单入手开始研究，有序思考，探索规律，再运用规律解决问题。

师：其实今天我们的研究方法与大数学家华罗庚先生所说的不谋而合（ppt出示华罗庚的话），也就是以退为进，化繁为简。

学生自己完整经历了解决最开始复杂问题的过程，总结出要多变少，有序地去找规律，在总结中理解了“化繁为简”这一解决复杂问题的核心思想方法。但学生只是一种模糊的感知，没有内化和系统，老师及时地进行小结并且将华罗庚先生“善于退，足够的退，退到原始而不失去重要性的地方，是学好数学的一个诀窍”的名言展示出来，给学生形成系统的认识，加深对化繁为简的理解。数学思想方法的渗透是润物无声的，但又要注意及时地总结和归纳，为学生点亮“思想方法”这盏明灯。

3.拓展延伸，打破定势

师：那现在看这个图形，一共有多少个三角形？谁可以快速地答出来。

……

生1：2019+2018+……+2+1（个）

生2：不对，这里线段不是斜著的，是横着的。上面是一个三角形，下面是梯形，梯形不是三角形。

师：看来有争论，数学课堂就需要这种不同的声音，真理越辩越明！那这个问题要怎样解决呢？

生：可以化繁为简，从简单入手开始研究，去找规律，再验证。

学生动手探索研究，解决问题。

学生在前面习得了“化繁为简”“有序”“转化”“变与不变”等数学思想，但同时得到了n+（n-1）+…+2+1这个规律，形成了思维定势。这道拓展题目摆出来，学生之间就产生了争论，通过生生争论，思维定势和理性思考激烈冲突，学生发现规律不再适用于这个题目。这时候自然而然就会想到要用数学思想解决这个问题。学生用争论打破定势，证明了重要的是思想方法而不是死记结论。数学思想方法是宏观的“通法”，与解决某个具体问题的“解法”不同，具有更好的适用范围，但学生往往会受思维定势等的影响，更容易记住“解法”，通过类似的争论等方法辅助思想方法的渗透，让这盏明灯越来越亮。

4.课后留疑，研精覃思

师：我们今天研究了这两种数三角形的方法。（课件）如果继续数三角形，你觉得可能研究哪一种？

生：一个大三角形里，既有横着加线又有竖着加线的。

师：这节课我们一起研究了数三角形。数学学习重方法，今天你们用到的“有序”“转化”“变与不变、化繁为简”等思想在以后的学习中会像明灯一样点亮你们学习的方向。这些思想在数长方形、正方形、梯形的时候是否也用得上呢？一个大三角形里，既有横着加线又有竖着加线的又怎样解决呢？留给你们课后去探索和研究！

在课堂的最后，引导学生自然抛出“一个大三角形里，既有横着加线又有竖着加线的共有多少个三角形”的问题，为学生课后探索提供素材，让学生可以通过课后的探索练习加深对思想方法的认识。同时是否用得上的问题引发学生思考，为以后学习数其他图形打下基础。数学思想方法不能止于课堂教学，课后也要留有问题，给学生丰富的思考空间，让学生在自己的探索和应用中融会贯通，成为以后数学学习的神兵利器。