基于Dd接线变压器及静止无功发生器的电气化铁路同相供电综合补偿方案
2020-08-06李群湛解绍锋
王 辉,李群湛,解绍锋,张 宇
(西南交通大学 电气工程学院,四川 成都 611756)
我国电气化铁路采用单相工频制(频率为50 Hz),取电于公用电网,目前电能质量问题以负序为主,通常采用轮换相序、分相分区供电的措施降低牵引负荷对电力系统公共连接点(Point of Common Coupling,PCC)处不平衡的影响[1-7]。因此,在分相分区处设置电分相,而电分相的存在会带来机车掉分相及带电过分相等安全隐患,同时带来施工选址受限等问题[8-11]。
国内外研究人员针对负序及电分相等问题进行了大量有益研究。德国电气化铁路取电于自建电厂或者公用电网,可解决负序及电分相等问题,但该供电制式自成体系,成本较高,应用范围有限[7]。俄罗斯等国电气化铁路广泛采用双边供电,该方式省去变电所间分区所处的电分相,但会产生均衡电流,存在穿越功率和继电保护配合等问题[7],同时负序问题仍未解决。日本采用功率融通装置虽然可实现负序等电能质量问题的治理[12-13],但电分相带来的问题仍未被解决。为解决电分相带来的问题,德国、法国和日本等国研究了过分相技术,但仍有不足,列车过分相技术存在列车掉速和过电压等问题,地面自动过分相技术投资相对较高,此外,受装置寿命影响,对施工选址亦有要求[14]。
我国西南交通大学李群湛教授于1988年率先提出同相供电概念[5],先后提出了基于三相一两相变压器构成的同相供电技术[6]和组合式同相供电技术[7]等,先后在成昆线眉山牵引变电所和山西中南通道沙峪牵引变电所成功进行试验,并在“国家示范工程”温州市域铁路S1线工程中成功商用。理论和工程实践表明,同相供电技术在解决负序等电能质量问题的同时,亦能消除牵引变电所出口处电分相带来的不利影响。
目前,青藏线、川藏线等线路电气化铁路建设对牵引供电提出了新的挑战,主要体现在外部电源薄弱,长、大坡道多,不宜过多设置电分相等。而以牵引变电所所群贯通供电技术为代表的长距离无分相贯通同相供电技术可作为解决上述挑战的有效手段之一。其中,负序集中补偿作为牵引变电所群贯通供电系统的关键技术之一,上述有源有功方式不再适用,应采用有源无功方式进行负序集中补偿。与传统使用晶闸管的无功补偿装置相比,静止无功发生器(Static Var Generator,SVG)具有调节速度快、运行范围广等优点[9]。
本文提出基于Dd接线变压器及SVG 的电气化铁路同相供电综合补偿方案,分别从2 端口补偿模式及3 端口补偿模式构建了同相供电综合补偿方案的数学模型,给出了同相供电综合补偿方案的控制策略,并通过仿真验证了同相供电综合补偿方案及控制策略的正确性和可行性。
1 基于Dd 接线变压器及SVG的同相供电综合补偿方案
以牵引变电所群贯通供电系统为代表的长距离无分相贯通同相供电系统的综合补偿方案为例进行分析。采用由Dd接线变压器及SVG 构成的负序补偿装置(Negative Sequence Compensation Device,NCD),对同相供电系统的负序进行集中补偿,牵引负荷均取电于电力系统AB 相,Dd 接线变压器以Dd0 接线方式为例。根据NCD 的结构(如图1所示),综合补偿方案分为2 端口补偿模式和3 端口补偿模式,2 端口补偿模式下无功补偿单元SVG1 和SVG2 分别连接至Dd0 接线变压器次边对应的bc和ca端口,3端口补偿模式下无功补偿单元SVG1,SVG2 和SVG3 分别连接至Dd0 接线变压器次边对应的bc,ca和ab端口。

图1 NCD结构示意图
牵引变电所群贯通供电系统如图2所示。图中:SSi为第i(i=1,2,…,n;n≥2)个牵引变电所;CD 为控制器,用于信号的输入和输出及潮流分析;CTS 为中心牵引变电所(Central Traction Substation),即当PCC 处负序超标时,选择在CTS 处设置NCD 进行负序集中补偿,补偿后PCC点处三相电压不平衡度达到国标要求。如图2所示:将电网同一变电站三相中相同两相(每相同一母线的不同分段)以辐射式结构给n个牵引变电所供电的这n个牵引变电所称为1 个牵引变电所群,群内各牵引变压器原边获得相同相位,次边牵引网贯通连接,构成长距离无分相贯通同相供电;除CTS 外,其余n-1 个牵引变电所为普通牵引变电所。牵引网以直供方式为例,同时也适用于AT 等其他供电方式。

图2 牵引变电所群贯通供电系统示意图
以3 端口补偿模式为例,将图2中的SS1作为CTS,对负序进行集中补偿,CTS 结构示意图如图3所示。图中:CT1和PT1分别为电流互感器和电压互感器,分别用于电压和电流信号的采集。

图3 3端口补偿模式下CTS结构示意图
综上,在CTS 处设置NCD,通过获取n个牵引变电所的牵引负荷情况,将相应牵引负荷的信号输入至CD,CD 输出信号控制NCD 实现负序和无功的综合补偿,构成同相供电综合补偿方案。进一步分析,n=1 时,可以描述为单所同相供电,仅采集CTS对应的牵引负荷数据。
2 同相供电综合补偿原理及数学模型
2.1 基本原理
相关国标规定负序的考核点在PCC[15],同相供电综合补偿方案旨在通过SVG 发出无功电流补偿牵引负荷的负序电流,使PCC 处负序满足相关国标要求[15],同时不会引起新的电能质量问题。以牵引工况下牵引负荷滞后为例,分别对2 端口补偿模式和3端口补偿模式下基本原理进行分析。
设由n个牵引负荷端口的牵引负荷电流合成的总牵引负荷电流IL为

式中:IλL为牵引负荷端口λ(λ=1,2,…,n)处的馈线电流。
1)2端口补偿模式下
2 端口补偿模式下负序补偿原理相量关系如图4所示。图中:UA,UB,UC和UAB,UBC,UCA分别为PCC 处A,B,C 三相电压的相电压和线电压的相量形式,对应的端口单位负序分量依次为U‾A,U‾B,U‾C和U‾AB,U‾BC,U‾CA;φL为IL滞后UAB的角度;I21和I22分别为2 端口补偿模式下SVG1 和SVG2 发出的无功电流,对应的负序电流分别为I‾21和I‾22。该补偿模式下,负序电流I‾21和I‾22合成负序电流-I‾L,即-I‾L=I‾21+I‾22,用来抵消IL产生的负序电流I‾L。

图4 2端口补偿模式下负序补偿原理相量图
2)3端口补偿模式下
同理,3 端口补偿模式下负序补偿原理相量关系如图5所示。图中:I31,I32和I33分别为3 端口补偿模式下SVG1,SVG2和SVG3发出的无功电流,对应的负序电流分别为I‾31,I‾32和I‾33。该补偿模式下,负序电流I‾31,I‾32和I‾33合成负序电流-I‾L,即-I‾L=I‾31+I‾32+I‾33,用来抵消IL产生的负序电流I‾L。

图5 3端口补偿模式下负序补偿原理相量图
对比2 种补偿模式下的补偿原理,区别在于较2 端口补偿模式,3 端口补偿模式增加了无功补偿单元SVG3,以补偿牵引负荷基波电流产生的负序电流。
2.2 综合补偿数学模型
在对PCC 处负序集中补偿的同时伴随着无功补偿,为使补偿后的负序和功率因数均满足相关国标要求[15],需对PCC 处负序及CTS处无功进行约束。在CTS 处进行集中补偿,总负荷产生的负序考核点在PCC 点,同时应确保CTS 处负荷功率因数满足要求。
定义无功补偿度KC作为补偿后CTS 处功率因数的约束因子,为

式中:k为补偿端口的数量,k=1,2,…,m,则2 端口补偿模式下m=2,3 端口补偿模式下m=3;Sk和φk分别为第k个补偿端口处的无功功率和功率因数角;S1L和φ1L分别为CTS处牵引负荷的视在功率和功率因数角。
式(2)中,KC表示为补偿装置的容性无功功率与CTS 处牵引负荷无功功率(S1Lsinφ1L)的比值。若第k个补偿端口处SVG 发出容性无功功率,则φk=-π/2,此时Sk>0;若第k个补偿端口处SVG发出感性无功功率,则φk=π/2。
设补偿前CTS 处牵引侧母线处牵引负荷功率因数为cosφ1L,补偿后为cosφ′1L。忽略损耗,SVG仅发出无功功率,补偿前后负荷有功功率不变,则cosφ′1L为

根据式(2)及式(3)得到KC的另一种表示形式为

式(4)中,当cosφ′1L≥cosφ1L时,KC≥0;当cosφ′1L<cosφ1L时,KC<0。
定义负序补偿度KN对PCC 处负序补偿进行约束[2],为
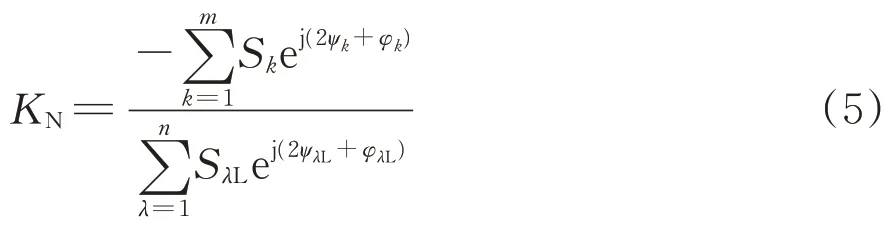
式中:ψk为补偿端口k处端口电压滞后UA的角度;SλL,φλL和ψλL分别为牵引负荷端口λ处牵引负荷的视在功率、功率因数角和端口电压滞后UA的角度。
式(5)中,KN表示补偿后PCC点处负序补偿量(减少量)与原有负荷造成的PCC 点处的负序功率的比值,通常KN取实数。
针对PCC 处负序限值,相关国标对相间单相负荷引起的负序电压不平衡度εU规定[15]为

式中:Sd为PCC 处短路容量;SL为单相总牵引负荷容量。
由式(6)得到负序功率允许值Sε为

补偿后总负荷的负序复功率S‾为

其中,

式中:ψL为总牵引负荷的端口电压滞后A相电压的角度。
根据式(5)、式(7)及式(8)得到负序功率的约束条件为|S‾|≤Sε,进一步表示为(1-KN)×SL≤εUSd,则KN≥1-εUSd/SL,即KN∈[1-εUSd/SL,1]。相关国标对三相电压不平衡度规定了不同的限值[15],为1.3%,2.6%,2%和4%,根据不同的限值及负荷取值可求出对应的KN值。
将式(5)按照实部与虚部展开,并与式(2)联立,得到负序与无功的综合补偿数学模型为

对于2 端口补偿模式综合补偿数学模型,由式(9)知此处KC不做约束,仅作为判断条件,根据式(3)对补偿后的功率因数进行校验。SVG1 和SVG2 发出的无功功率分别为S21和S22,为便于分析,假设φ1=φ2=-π/2,根据式(9)得到2 端口补偿模式下的综合补偿数学模型为

其中,ψ1=π/2;ψ2=-5π/6;θL=2ψL+φL。
由式(10)可得S21和S22分别为

式(11)和式(12)中,若S2k(k=1,2)>0,则表示SVG 发出容性无功功率;若S2k(k=1,2)<0,则表示SVG 发出感性无功功率。由于各端口电压相同,由式(11)和式(12)分别得到SVG1与SVG2发出的电流I21和I22大小分别为

式中:kL为牵引变压器变比;UL为牵引负荷端口电压;kM为Dd0 接线变压器变比;UM为补偿端口电压。
同理,式(13)和式(14)中,若I2k(k=1,2)>0,则表示SVG 发出容性电流;若I2k(k=1,2)<0,则表示SVG发出感性电流。
相较于2 端口补偿模式,3 端口补偿模式下综合补偿数学模型负序电流由SVG1,SVG2 和SVG3 共同进行补偿,SVG1,SVG2 及SVG3 发出的无功功率分别为S31,S32和S33。同理,令φ1=φ2=φ3=-π/2,根据式(9)得到3 端口补偿模式下综合补偿数学模型为
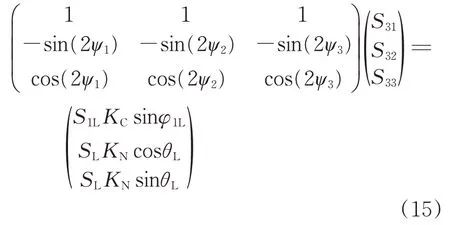
其中,ψ3=-π/6。
由式(15)求解得到S31,S32和S33分别为
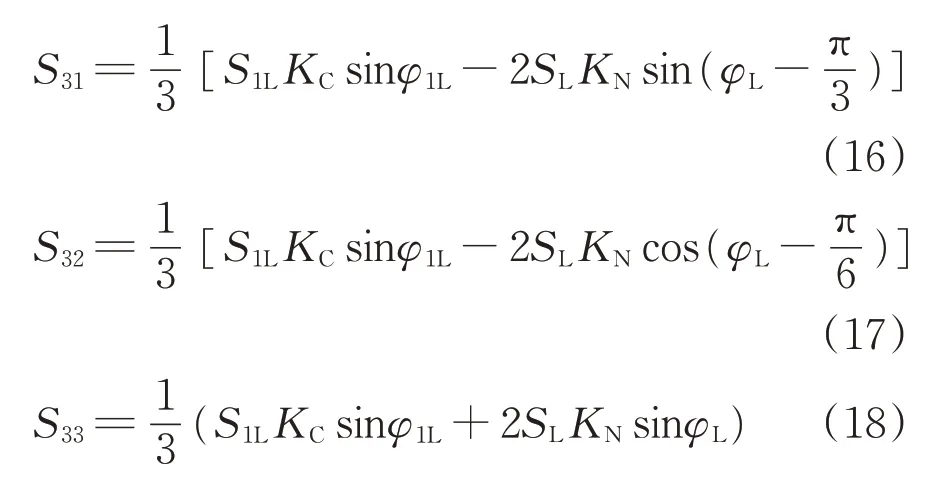
式(16),式(17)和式(18)中,若S3k(k=1,2,3)>0,则表示SVG 发出容性无功功率;若S3k(k=1,2,3)<0,则表示SVG 发出感性无功功率。
同理,由式(16),式(17)和式(18)分别得到SVG1,SVG2 及SVG3 发出的电流I31,I32和I33的大小分别为
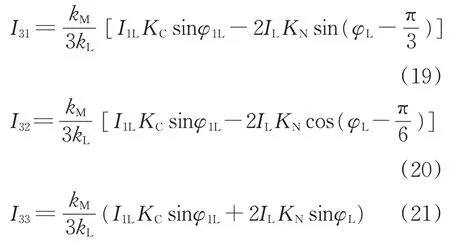
式(19),式(20)和式(21)中,I3k(k=1,2,3)>0,表示SVG 发出容性电流;I3k(k=1,2,3)<0,表示SVG 发出感性电流。对于3 端口补偿模式,由式(16)、式(17)和式(18)知,当负荷功率因数为1时,此时不需在补偿端口增加SVG3,仅仅依靠SVG1 与SVG2 则可以实现负序的完备补偿,同时CTS处的功率因数不受影响。
相关国家标准规定谐波在PCC 处考核[16],因此,上述2 端口补偿模式和3 端口补偿模式可兼顾一定的谐波补偿作用。具体原理如下。
(1)2 端口补偿模式下,通过SVG1 和SVG2分别产生补偿谐波电流I1H和I2H,二者合成与机车谐波电流大小相等、相位相反的补偿电流,达到补偿PCC 点处谐波电流的目的。牵引负荷谐波电流为ILH,根据绕组电流分布情况,得到I1H和I2H分别为I1H=ILHkM/kL和I2H=ILHkM/kL。
(2)3 端口补偿模式下,除采用上述2 端口补偿模式的方法外,只需SVG3产生与牵引负荷谐波电流大小相等、相位相反的补偿电流即可达到补偿PCC 处谐波电流的目的。根据绕组电流分布情况,得到SVG3需补偿的谐波电流I3H=-ILHkM/kL。
因此,在补偿负序电流的同时还具备在PCC处补偿谐波电流的功能。当牵引负荷功率因数为1 时,由式(11)和式(12)知,此时SVG1 和SVG2 的容量相同,1 个容性端口,1 个感性端口,补偿后CTS 处功率因数不变。对于牵引负荷功率因数不等于1 时的负序全补偿,2 端口补偿模式补偿范围是有限的,若补偿后CTS 处功率因数满足要求,则2 端口补偿模式可行,否则采用3 端口补偿模式。对于3 端口补偿模式,设定合适的KN和KC即可实现负序的治理。此外,考虑到负序允许值,当牵引负荷的无功分量产生的负序在规定的范围内,可通过2 端口补偿模式补偿牵引负荷有功分量产生的负序。
2.3 补偿方案的确定
基于计算机仿真获取牵引负荷端口λ对应的不同时刻t1,t2,…,tN1对应的负荷过程数据SλL(t1),SλL(t2),…,SλL(tN1);分别根据式(11)和式(12)确定2 端口补偿模式下补偿端口k对应的SVG 容量S2k(t1),S2k(t2),…,S2k(tN1),分别根据式(16)、式(17)和式(18)计算3 端口补偿模式下补偿端口k对应的SVG 容量S3k(t1),S3k(t2),…,S3k(tN1);定义2 端口补偿模式下和3 端口补偿模式下的最大无功补偿量分别为Q2Σ和Q3Σ,如式(22)和式(23)所示,最大无功补偿量越大,需要的SVG装置也容量越大。

式中:t∈{t1,t2,…,tN1}。
综上,得到确定补偿模式的流程图如图6所示。
3 控制策略
设定牵引负荷端口电压瞬时值uL(t)为

式中:UL1为基波电压有效值;ω为角频率,ω=2πf,f为频率。
设定牵引变电所端口馈线电流瞬时值iL(t)为

图6 补偿模式确定流程图
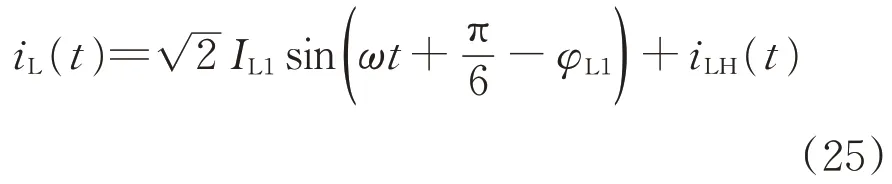
式中:IL1为基波电流有效值;iLH(t)为t时刻谐波电流瞬时值;ILh和φLh分别为h(h≥2)次谐波电流的有效值和相位。
将负载电流iL(t)的基波电流表示成基波有功电流分量iLp(t)和基波无功电流分量iLq(t)的形式,则式(25)可表示为

其中,

式中:ILp和ILq分别为基波电流相量有功分量和无功分量的有效值。
将式(26)分别乘以sin(ωt+π/6)和cos(ωt+π/6),得到瞬时功率pLp和pLq分别为

根据式(26)和式(27),得到pLp和pLq的直流分量p0Lp=ILp/2和p0Lq=-ILq/2,则ILp=ILcosφL=
p0Lp,ILq=ILsinφL=p0Lq。
3.1 2端口补偿模式下控制策略
Ubc,Uca经锁相环PLL 产生同步信号cos(ωt-π/2)和cos(ωt+5π/6),牵引工况下SVG1和SVG2分别为容性和感性端口,可得到对应的同步信号分别为cos(ωt-π/2)和-cos(ωt+5π/6),补偿后SVG1和SVG2的期望补偿电流理论值i′21和i′22分别为

将期望补偿电流理论值与实际电流比较,经PI 环节,利用三角波调制产生控制SVG 的驱动信号[17-18]。综上,得到2 端口补偿模式的控制策略原理框图如图7所示。图中:LPF为低通滤波器。
3.2 3端口补偿模式下控制策略
Ubc,Uca和Uab经锁相环PLL 产生的同步信号cos(ωt-π/2),cos(ωt+5π/6)和cos(ωt+π/6),牵引工况下SVG1,SVG2 及SVG3 分别为容性、感性和容性端口,则同步信号分别为cos(ωt-π/2),-cos(ωt+5π/6)和cos(ωt+π/6),期望补偿电流理论值i′31,i′32和i′33分别为


图7 2端口补偿模式控制策略原理框图

3 端口补偿模式中的SVG 控制原理框图与2 端口补偿模式相似,此处不再详细介绍。综上,3 端口补偿模式补偿电流检测框图如图8所示。
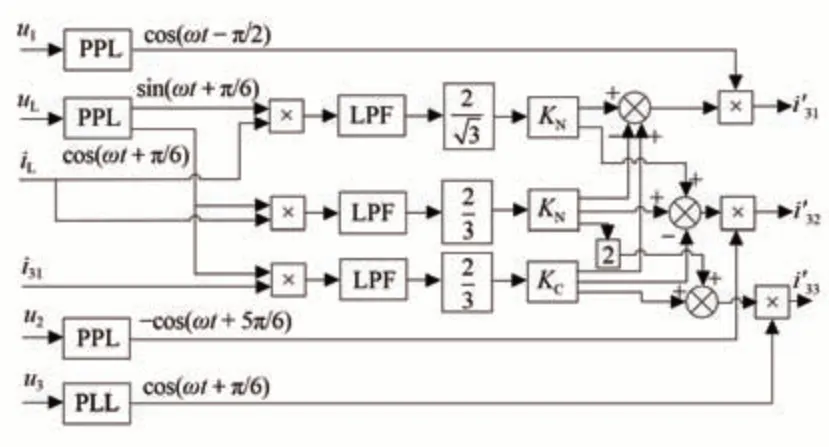
图8 3端口补偿模式补偿电流检测框图
4 仿真分析
为了验证上述综合补偿方案的有效性,分别进行如下仿真分析。
4.1 单所同相供电2端口补偿模式下
单所同相供电仿真条件如下:PCC 处短路容量为1 500 MV·A,牵引变压器为单相变,变比为110 kV/27.5 kV。
不考虑牵引负荷谐波时,设定牵引负荷视在功率和功率因数分别为25MV·A 和0.98,补偿前原边三相电流如图9(a)所示;采用2 端口补偿模式完全补偿(补偿后三相电压不平衡度期望值εU1为0%,即KN=1)和部分补偿(εU1为1.3%,即KN=0.22)后的原边三相电流分别如图9(b)和图9(c)所示。

图9 不考虑牵引负荷谐波时的单所同相供电补偿结果
考虑牵引负荷谐波时,补偿前原边三相电流如图10(a)所示;采用2 端口补偿模式完全补偿(εU1为0%,即KN=1)和部分补偿(εU1为1.3%,即KN=0.22)后的原边三相电流分别如图10(b)和图10(c)所示。
对PCC 处对应的波形数据进行傅里叶分解及相关计算[15],结果见表1。由表1可以看出:不考虑牵引负荷谐波时与考虑牵引负荷谐波时的负序补偿结果基本一致,说明负序补偿与谐波补偿是独立的。
以不考虑牵引负荷谐波仿真结果为例,统计2个补偿端口SVG的容量见表2。由表2可以看出:在满足相关国标要求的前提下[15],采用部分补偿后,就可以降低SVG补偿装置的容量。
对考虑牵引负荷谐波的仿真结果进行分析,统计原边三相处电流与三相电压的总谐波畸变率见表3。由表3可以看出:补偿后谐波电流和电压都有所降低,说明综合补偿方案在补偿负序的同时可以兼顾在PCC处补偿牵引负荷引起的谐波电流。

图10 考虑牵引负荷谐波时的单所同相供电补偿结果

表1 负序及功率因数统计结果

表2 SVG容量统计结果 MV·A
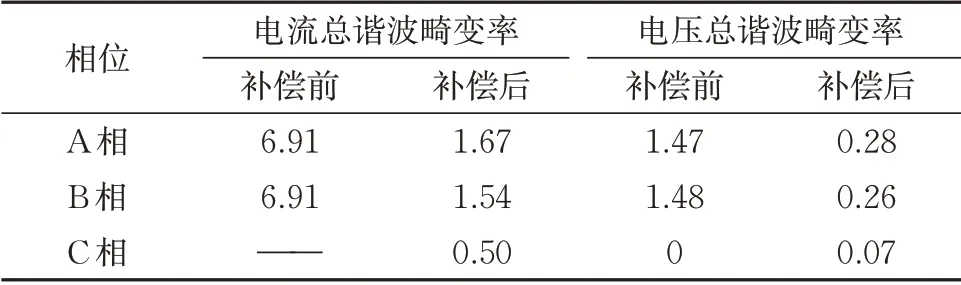
表3 电流与电压总谐波畸变率 %
进一步分析不考虑牵引负荷谐波时的单所同相供电补偿的最大无功补偿量,并绘制对应的功率因数曲线,如图11所示。其中,补偿后的三相电压不平衡度满足:0≤εU≤1.3%,即0.22≤KN≤1。由图11可以看出:不同的KN取值对应于不同最大无功补偿量以及功率因数;因此,通过合理确定KN的值,达到补偿的同时兼顾经济性。

图11 不考虑牵引负荷谐波时的最大无功补偿量和功率因数
4.2 牵引变电所群贯通供电系统补偿仿真分析
部分仿真条件如下:群中牵引变电所数目为3 个,系统短路容量仍为1 500 MV·A;牵引变压器均为单相变,变比均为110 kV/27.5 kV;设定SS1(为CTS),SS2 和SS3 的牵引负荷大小分别为20,23 和25 MV·A,功率因数均为0.98。补偿前PCC点处三相电流如图12(a)所示。
采用2 端口补偿模式完全补偿后(εU1为0%,即KN=1),PCC 处三相电流如 图12(b)所示,SS1 处的功率因数为0.55,SS2 和SS3 的功率因数均为0.98,PCC 处补偿后三相电压不平衡度实际值εU2为0.08%,负序补偿达到期望值。但是SS1的功率因数小于0.9 不满足要求,此时应该考虑3端口补偿模式。
采用3 端口补偿模式,①设定KN=1(εU1为0),KC=0(补偿后功率因数cosφ′1L期望值为0.98)PCC处三相电流如图12(c)所示,补偿后功率因数实际值cosφ′2L为0.97,εU2为0.08%,与预期设定基本一致;②设定KN=0.71 (εU1为1.3%),KC=0(cosφ′1L为0.98),PCC 处三相电流如 图12(d)所示,cosφ′2L为0.96,εU2为1.31%,与预期设定基本一致。
上述结果表明,对于功率因数不为1 的牵引负荷负序的全补偿,2 端口补偿是不完备的,而3 端口补偿是完备的,该情形下推荐3端口补偿模式。
进一步分析3 端口补偿模式的最大无功补偿量,设定补偿后CTS 的功率因数满足cosφ′1L≥0.98,即0≤KC≤1;补偿后的三相电压不平衡度满足0≤εU1≤1.3%,即0.71≤KN≤1,其他参数设置相同,则得到3端口补偿模式下的最大无功补偿量如图13所示。

图12 牵引变电所群贯通供电仿真结果

图13 3端口补偿模式最大无功补偿量
由图13可以看出:当KN与KC不同时,最大无功补偿量也不同,即对应的SVG 容量也不同。因此,考虑到经济性以及设备的容量,应合理配置补偿后的KN和KC。
5 结 语
针对电气化铁路以负序为主的电能质量问题,本文提出了基于Dd变压器及SVG 的电气化铁路同相供电综合补偿方案。将该方案分为2 端口补偿模式和3 端口补偿模式,构建了相应的综合补偿数学模型,定义了最大无功补偿量,将其作为确定综合补偿方案的依据,给出了确定综合补偿方案的流程图,针对不同补偿模式提出了相应的控制策略,通过仿真验证了本文综合补偿方案及控制策略的正确性和可行性。此外,研究表明本文方案在实现公共连接点处负序综合补偿的同时能够兼顾该处牵引负荷可能引起的谐波的补偿。
相较负序全补偿,采用负序部分补偿后,在一定程度上能够降低各端口SVG 的容量,考虑到经济性以及设备的容量,应合理配置补偿后的负序允许值以及功率因数。因篇幅有限,SVG 装置的容量配置将在后续文章中进一步说明。
