精密三角高程代替二等水准测量的研究
2020-08-06杜文举景淑媛
杜文举 张 恒 景淑媛
(四川建筑职业技术学院,四川德阳 618000)
目前,关于三角高程测量方面的论著较多:文献[1]认为,三角高程可以代替一等水准测量,但需要采用高精度电子全站仪及大气稳定或夜间观测的条件下才能达到,且容易超限,目前未见推广使用;而文献[3]和文献[4]表明,全站仪三角高程测量可达三、四等水准测量的精度。在山区,由于受到地形地势的影响,水准测量外业作业特别困难,在极端的地形条件下,有时不能满足二等水准测量的技术要求,造成时间和人力的浪费。以下利用两种不同精度的全站仪,对采用精密三角高程方法代替二等水准测量进行研究和分析。实验及分析表明,在一定条件下,该方法满足二等水准测量的精度要求,可以用于二等水准测量控制网的布设,有利于提高水准测量的效率。
1 三角高程测量原理
三角高程测量是通过观测两个控制点的水平距离和竖直角求定两点间高差的方法。其观测方法简单,受地形条件限制小,是测定大地控制点高程的基本方法。如图1所示,M、N为地面上两个高程控制点,M点架设全站仪,N点架设棱镜,分别量测仪器高i和棱镜高v,在顾及大气折光和地球曲率影响的条件下,M、N两点之间的高差hMN为
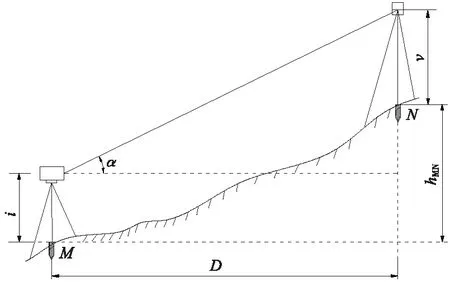
图1 三角高程测量
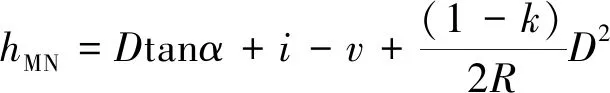
(1)
式中,D为M、N间的水平距离,R为地球曲率半径,α为M、N两点间的竖直角,k为大气垂直折光系数(与气温、气压和大气密度有关,不容易测出)。
2 误差来源分析
根据误差传播定律,对式(1)进行微分,经整理后得
(2)
影响高差精度的主要因素为以下几点。
(1)测角误差mα
测角误差取决于电子全站仪的精度,若采用南方NTS-342R6A,mα可达±2″;为提高测角精度,可选用徕卡TM50全站仪,其测角精度为0.5″,测距精度为(0.6+1×10-6D)mm,通过2个测回的观测,mα可达±0.3″~±0.5″。mα与距离D的平方成正比,故距离D不宜太长,原则上不超过600 m。
(2)测距误差mD
测距误差取决于全站仪的测距精度,若采用南方NTS-342R6A,mD=±(2+2×10-6D) mm,若采用徕卡TS50全站仪,mD=±(0.6+1×10-6D)mm。
(3)大气垂直折光系数k
大气垂直折光系数是光线穿透大气的角度比值,随气温、气压、日照、时间、地面情况和视线高度等因素而改变。通常情况下,k=0.08~0.14,一般取其平均值0.14。垂直角最佳观测时间段为10:00~16:00,可以通过往返对向观测进行气压改正后再取平均值,有利于减少k值的影响。文献[5]表明,折光系数k的中误差为±0.03~±0.05。
(4)仪高i和棱镜高v
在精密三角高程测量中,可以通过建立稳定的观测墩,再量取仪高和棱镜高,采用经过检定的条形钢尺在4个方向上量取仪高和棱镜高。此种条件下,i和v的精度可达0.3~0.5 mm[1-2]。
3 精度分析
在式(2)中,令
则得
m1为测角误差,m2为测距误差,m3为大气折光误差,m4为量取仪器和棱镜高误差。
不同品牌型号的全站仪测角精度不同,若是2″级的全站仪,两测回测角精度可达1.5″[6],若是1″级的全站仪,两测回测角精度可达0.7″~1.0″,若是0.5″级的全站仪,两测回测角精度可达0.3″~0.5″。
当mD=±(2+2×10-6D)mm,mα=±1.5″,mK=±0.04,按距离和竖直角的不同,分别对测角、测距和大气折光引起的误差进行计算,各项误差数据见表1。表1中①、②、③分别表示测角误差、测距误差和大气折光误差。
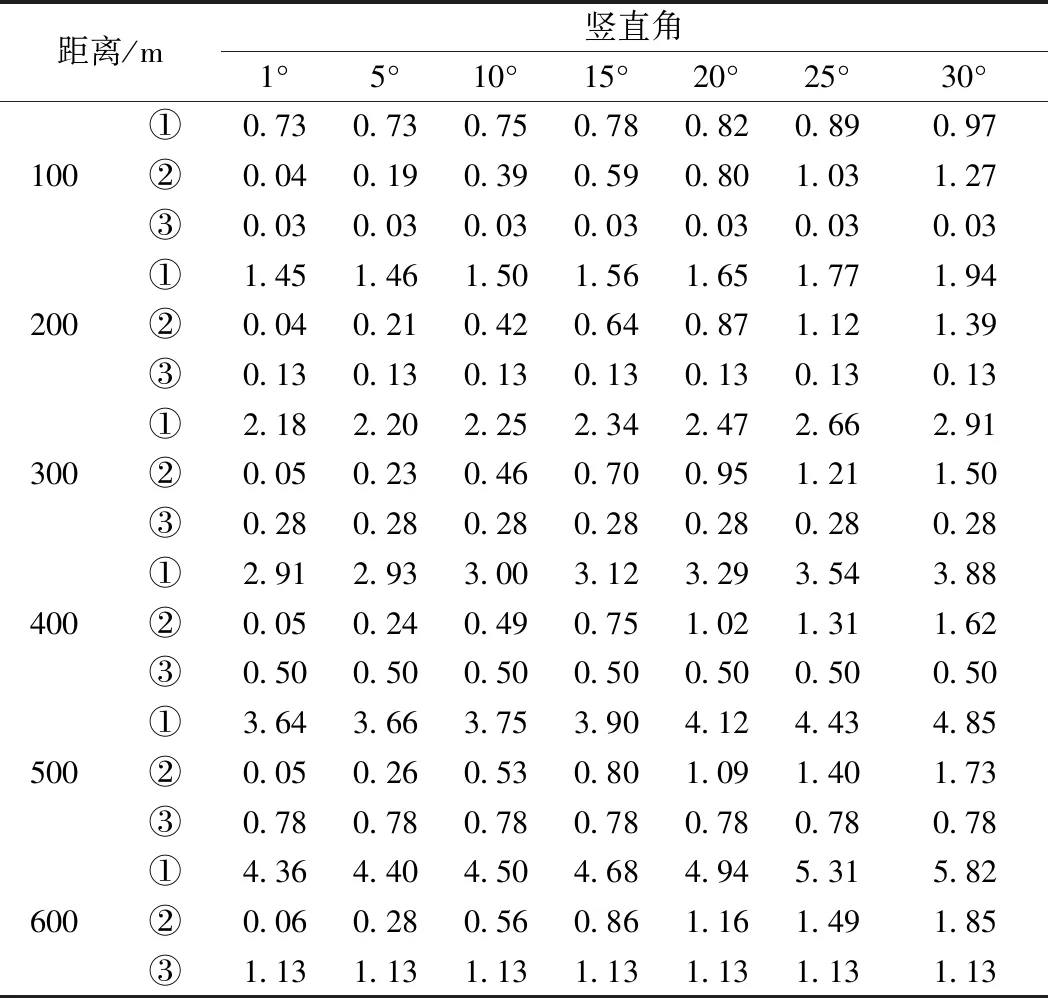
表1 2″级全站仪距离和竖直角变化引起的误差
当mD=±(0.6+1×10-6D)mm,mα=±0.5″,mK=±0.04,按距离和竖直角的不同,分别对测角、测距和大气折光引起的误差进行计算,各项误差数据见表2。表2中①、②、③分别表示测角误差、测距误差和大气折光误差。
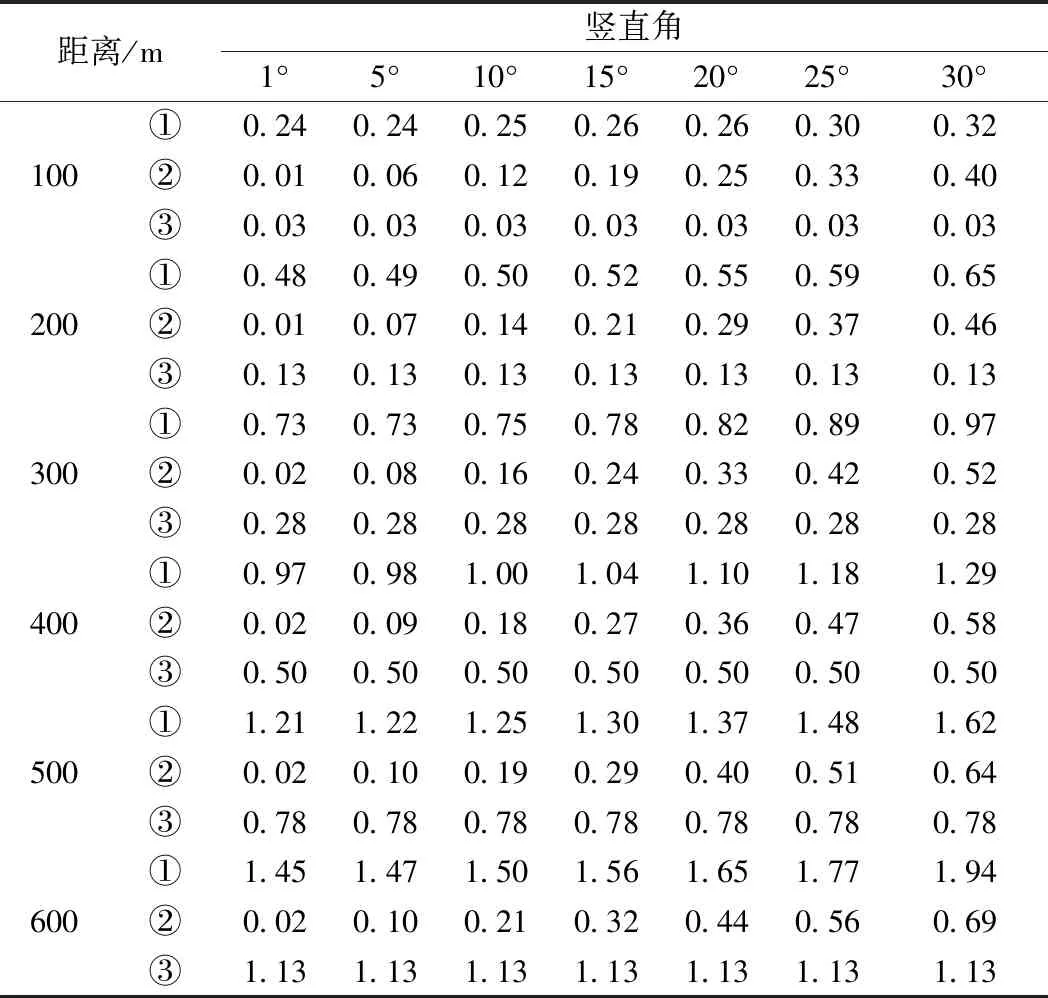
表2 0.5″级全站仪距离和竖直角变化引起的误差
由表1和表2可知,随着竖直角的增加,测距误差变大,但幅度较小;随着距离的增加,测角误差急剧变大,且幅度很大;随着距离的增加,大气折光误差渐渐变大,当距离接近600m时,大气折光误差突然变大;由此看出,和测角误差相比,测距误差的影响较小,测角误差是主要误差来源,故竖直角测量误差是引起高差测量误差的主要因素。因此,提高高差测量精度的关键是减小竖直角测量误差。为提高竖直角测量误差精度,可采用高精度全站仪提高测角精度,也可以通过增加竖直角测回数相对提升测角精度。
4 每千米高差中误差分析
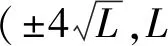
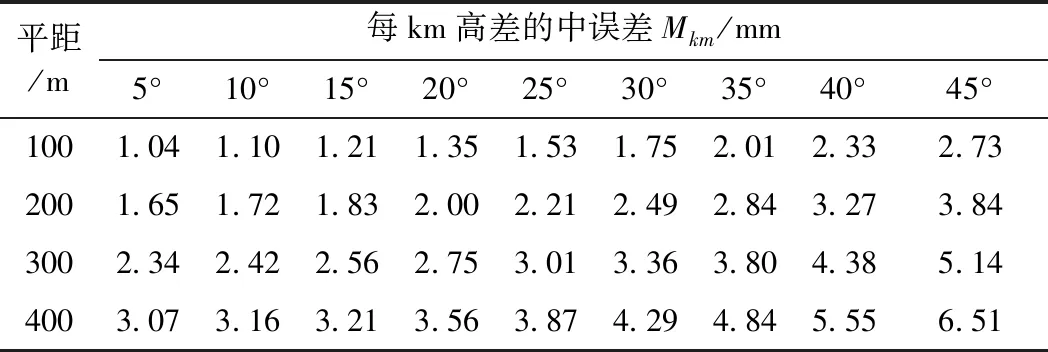
表3 每km高差的中误差
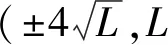
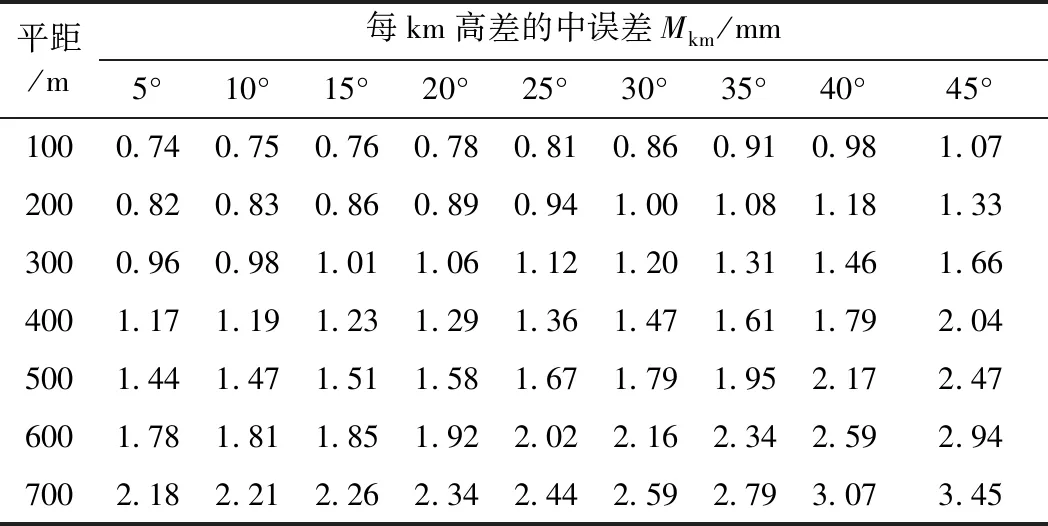
表4 每km高差的中误差
从表3和表4可见,随着竖直角和距离的增加,每公里高差的中误差逐渐变大,而仪高和棱镜高测量误差对高差中误差的影响是固定值,在竖直角和距离较小时影响较大,随着竖直角和距离的增大,影响变小。
5 试验应用分析
选择一闭合导线进行观测,采用2″级全站仪南方NTS-342R6A, 测角精度为±2″,测距精度为±(2+2×10-6D)mm,未采用固定墩,外业观测数据和计算成果如表5所示。
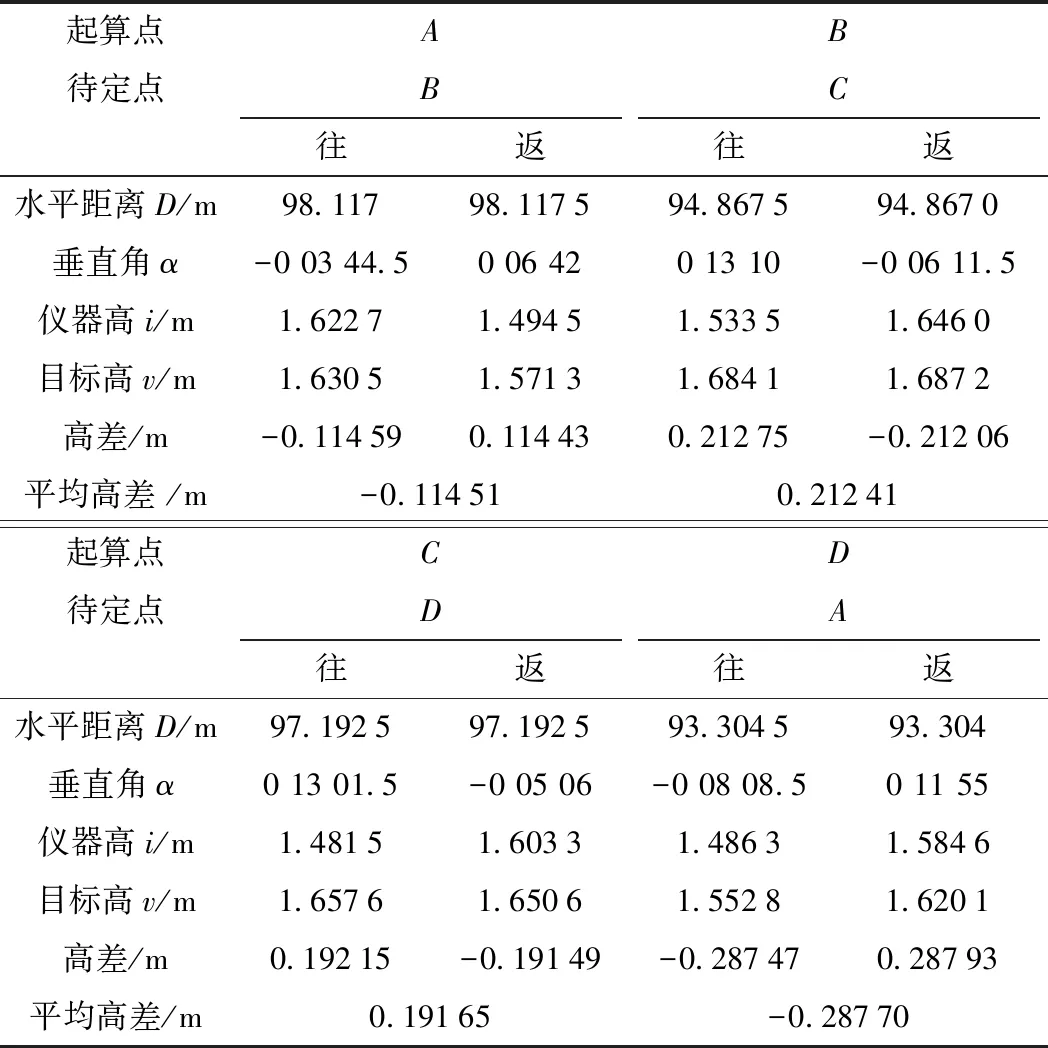
表5 对向观测数据及计算成果
上述路线二等水准闭合差限差为,而实测闭合差为1.8 mm,满足二等水准测量要求。
为了验证TM50全站仪(测角精度±0.5″,测距精度(0.6+1×10-6D)mm)三角高程测量的精度,在德阳东山选择一个高差较大的两处分设A点和B点,首先采用电子水准仪进行往返测量,往测24个测站,返测24个测站。有一个测站两点高差过大,两点距离不足30 m,测站点选择非常难(两测点位于陡坎一上一下,无法满足二等水准视线高度最低观测值的技术要求)。后对陡坎进行处理,勉强实现了前后点数据测量。经过计算,hAB=23.420 95 m,实际测量时间为2 d;而采用TM50全站仪观测,在AB两点之间加设一点,全程采用对向观测[14-15](竖直角不超过14°,最大距离255 m),测得hAB=23.418 83 m,AB两点距离约0.34 km,按二等水准要求,实测三角、水准高程较差为2.12 mm,满足二等限差要求,实际作业时间为0.5 d,时间和效率显著提高。
6 结论
高差误差的来源主要为测角误差。为提高测角精度,应优先选用高精度全站仪。当采用高精度全站仪进行三角高程测量时,需选择早晚气象稳定、外界噪声影响较小的环境下进行,可以保证竖直角和距离测量的稳定性。同时,竖直角观测至少3个测回以上。固定墩表面尽可能平整,以减少棱镜和仪器量测误差及后续高程控制误差。根据中误差公式推导和实验论证,证明在一定条件下,采用精密三角高程测量代替二等水准可以实现。
