幂函数变换的GM(1,1)模型在高铁沉降预报中的应用
2020-08-06范少杰
范少杰
(中国铁路设计集团有限公司,天津 300251)
高速铁路施工过程中,沉降监测与预报是铁路建设、运营、维护的重要环节。高速铁路施工沉降变形一般随着时间推移呈规律性变化,利用高精度的预报模型可以为高铁施工提供可靠的依据。已有许多学者进行了相关研究:甄亚男针对不同区域采用不同模型进行了沉降预报[1];刘生荣用多项式拟合和GM(1,1)模型进行高铁沉降预报[2];周兴华等利用双曲线模型对高速铁路沉降进行预报,发现其结果与实测数据的变化趋势基本一致[3];薛骐等针对沉降预报模型单一、预测结果不稳定等问题,提出采用小波神经网络进行高铁沉降预报[4-5]。之后,张松等利用时间序列对地铁进行短期沉降预报,证明时间序列可以用在短期沉降预报上[6];陈晨等利用灰色模型和Kalman滤波对初始值进行去噪处理及沉降预报,进一步提高了预测的精度[7-13]。
根据高速铁路沉降变化的特点,传统GM(1,1)模型具有一定的局限性:当原始数据观测值波动较大、光滑度不足时,易出现预测结果误差浮动较大的问题。由此可见,传统GM(1,1)模型预测精度取决于初始数据的光滑度[14]。针对这个问题,宋建强在进行货运量预测时,提出通过幂函数变换提高原始观测数列的光滑度,以降低其预测误差[15-16]。
以下结合某高铁沉降监测数据,将其初始观测数列进行平滑处理,利用MATLAB编程,对高铁沉降进行预报,并与传统GM(1,1)模型预报结果进行对比,以验证改进模型在高铁沉降预测中的适用性。
1 灰色理论模型原理与方法
1.1 传统GM(1,1)模型
首先,给定某一预测对象的非负原始数据列
x(0)(t)={x(0)(1),x(0)(2),…,x(0)(n)}
(1)
建立灰色预测模型,对x(0)(t)进行一次累加(1-AGO),生成一次累加序列
x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}
(2)
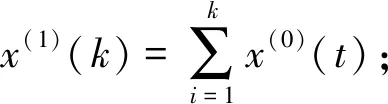
建立一个灰色微分方程,即GM(1,1)模型,有
x(0)(k)+α·z(1)(k)=u
(3)
z(1)(k)=0.5·x(1)(k)+0.5·x(1)(k-1)
(4)
其中,k=2,3,…,n;z(1)(k)为紧邻均值生成序列。
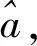
(5)
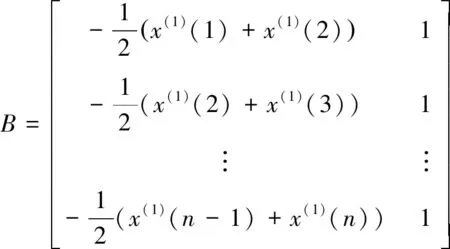
(6)
yn=[x(0)(2),x(0)(3),…,x(0)(n)]T
(7)
将求得的参数α、u值代入时间响应函数,有
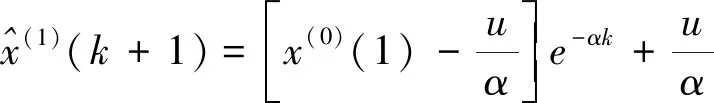
(8)
之后,累减还原得到的预测模型为
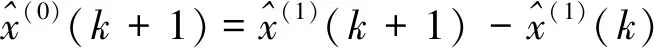
(9)
上述即为传统GM(1,1)模型的基本推导过程,对应高铁沉降预报时,自变量k为沉降监测的期数,应变量x为对应于期数k的沉降量。式(9)为累减还原后的沉降预报结果。
1.2 基于幂函数变换的GM(1,1)模型
针对传统GM(1,1)模型的缺陷,利用幂函数变换法对模型进行改进,以提高原始数据数列的光滑度,进而降低预报结果的预测误差。
基于幂函数变换的GM(1,1)模型的建模过程如下。
首先,设原始数据列为
y(0)(t)={y(0)(1),y(0)(2),…,y(0)(n)}
(10)
对原始数据进行幂函数变换
x(0)(t)={x(0)(1),x(0)(2),…,x(0)(n)}
(11)
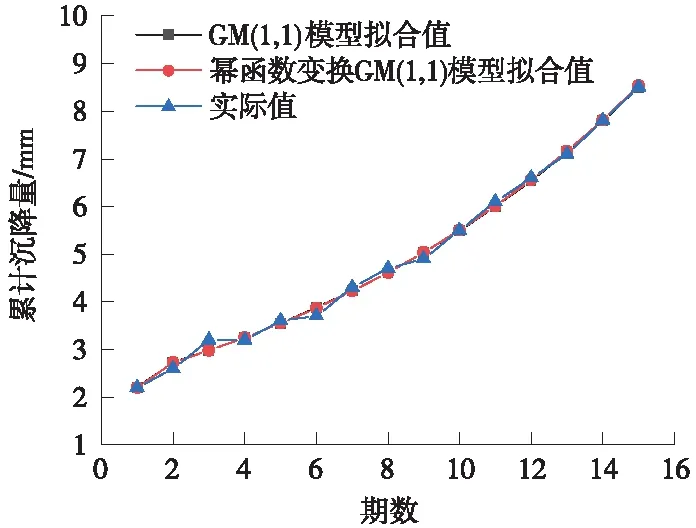
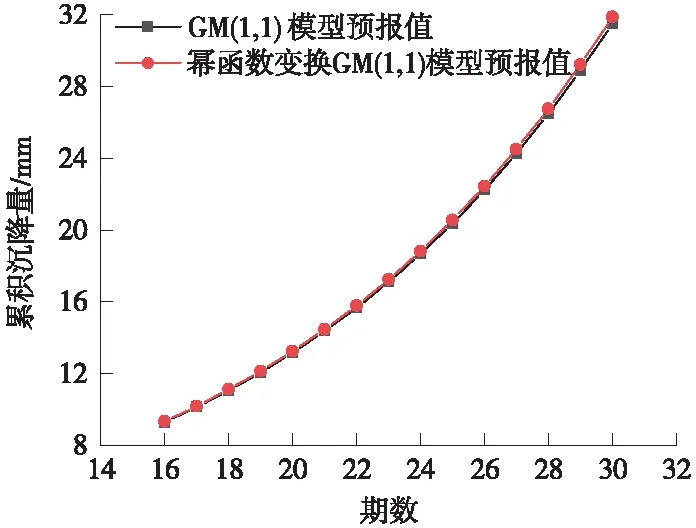
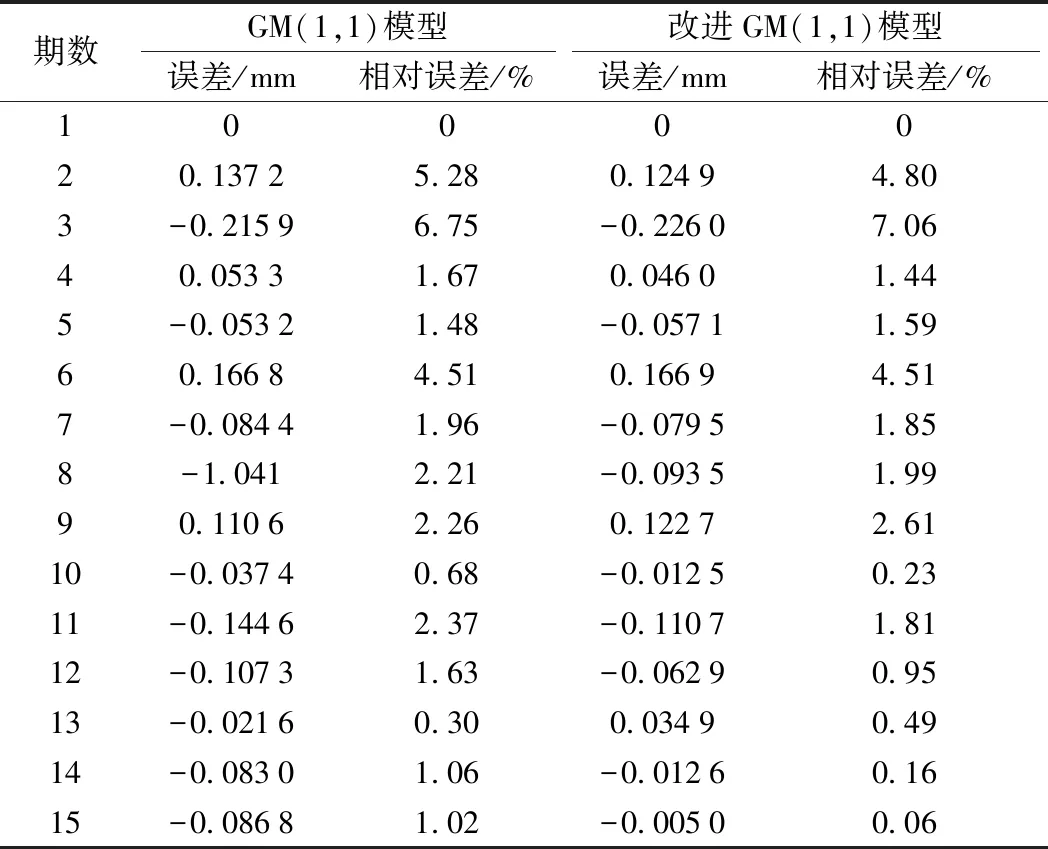
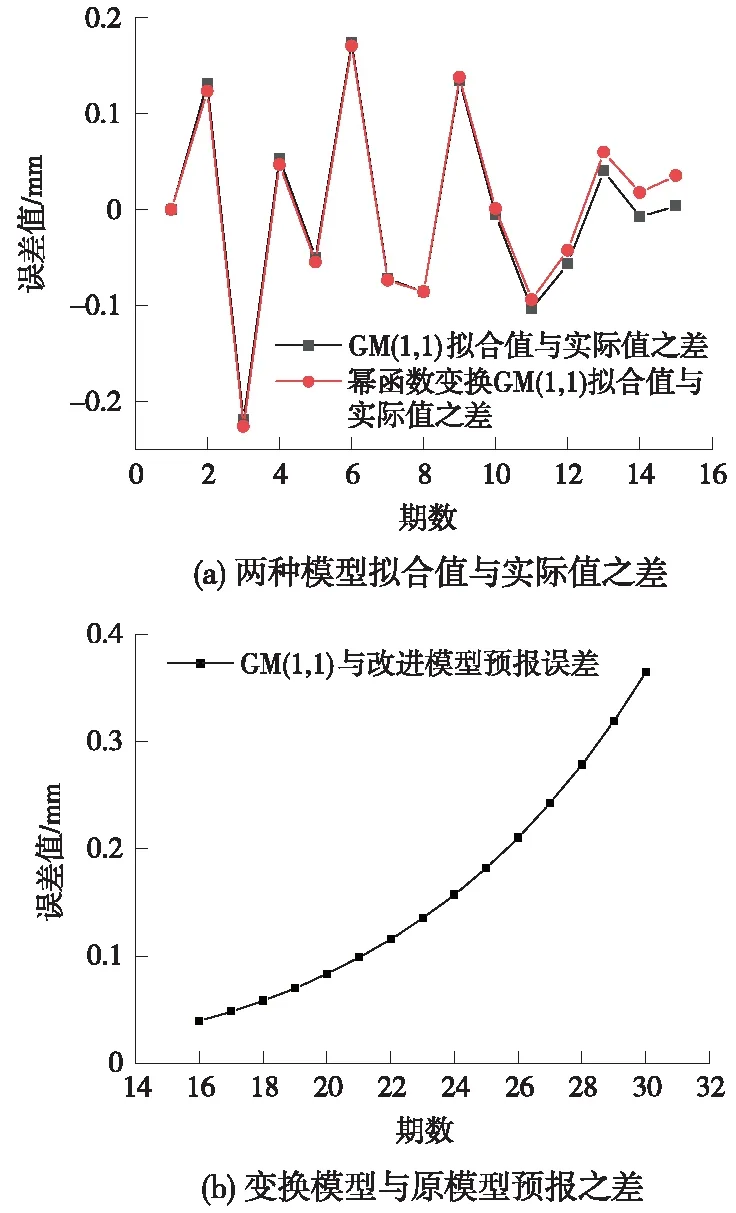
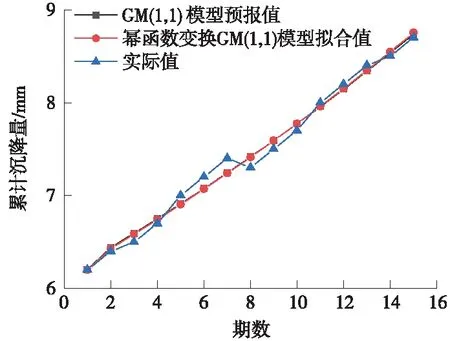
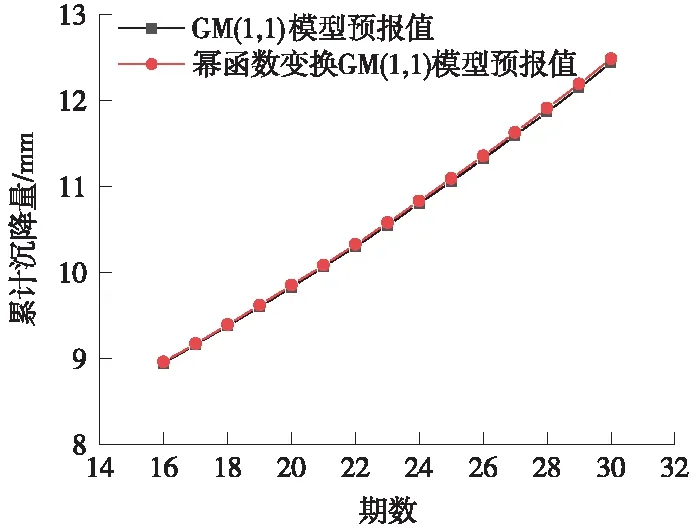
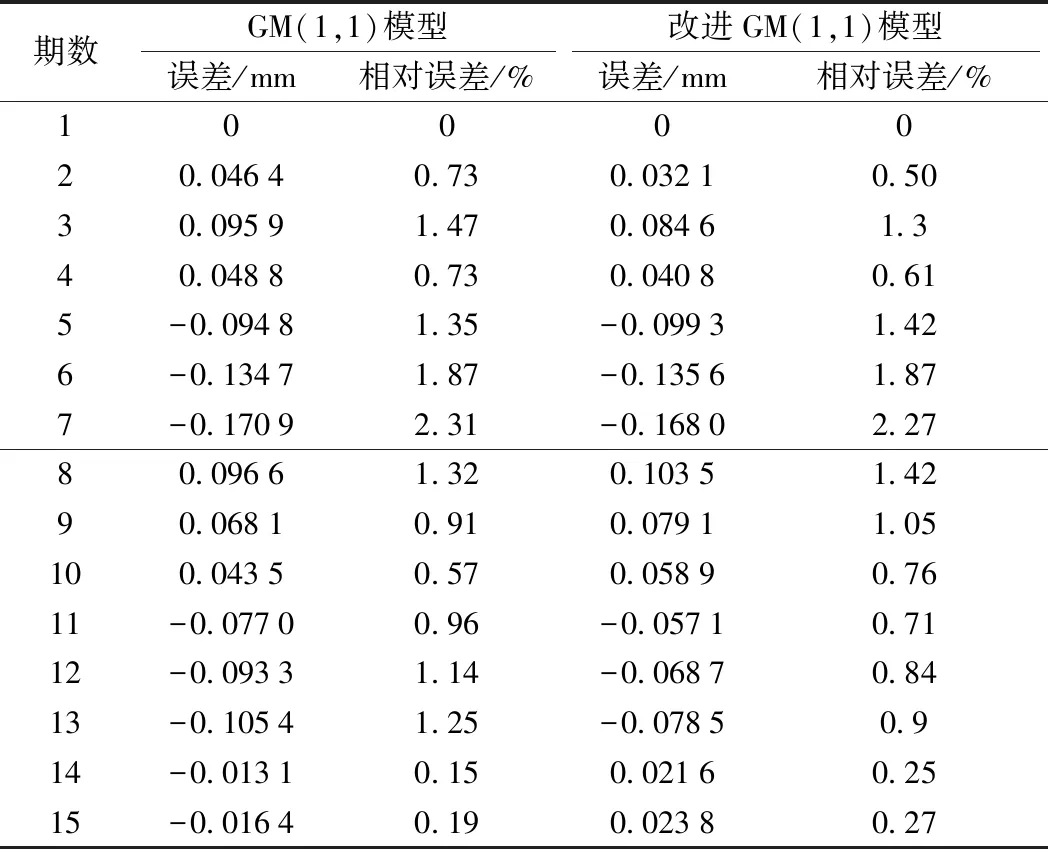
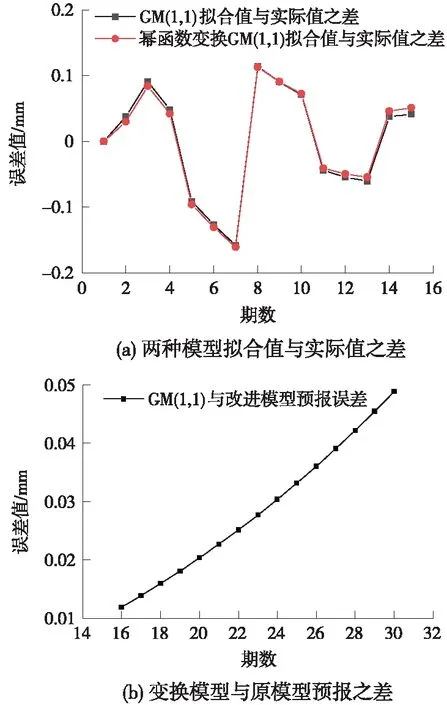
其中,x(0)(t)=[y(0)(t)]-a,t=1,2,…,n,0 其次,对x(0)(t)进行一次累加(1-AGO)生成一次累加序列 x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)} (12) (13) (14) (15) 将求得的参数α、u值代入时间响应函数,有 (16) 累减还原后得到的预测模型为 (17) 最后,将函数还原后即可得到预测数据 (18) 利用幂函数做变换,即可得到改进的GM(1,1)模型,y为高铁基本初始观测沉降序列,x为幂函数平滑处理后的沉降序列,k为沉降观测的期数,式(18)为幂函数还原出的预报沉降结果。 某高铁施工过程中,通过对现场沉降控制点进行监测,得到了各沉降点的变形数据。为检验改进模型的准确性和适用性,选择两个监测地点的各一组1~15期的监测数据作为基础数据,分别以GM(1,1)模型和基于幂函数的GM(1,1)模型对16~30期的沉降量进行预报,并且将拟合结果和实际测量值进行对比分析和精度比较。 原始观测数据见表1。 表1 原始观测数据 mm 根据第一组原始观测数据,利用传统GM(1,1)模型和幂函数变换的GM(1,1)模型分别进行拟合,可以得到如图1、图2所示的结果。 图1 第一组两种模型拟合结果 图2 第一组两种模型预报结果 根据两种模型计算出的结果与实测数据,可以得到如表2所示结果。 表2 第一组数据的预测精度对比 根据表2的误差结果,可以得到如图3(a)所示误差变化趋势,前10期数据中,传统GM(1,1)模型和基于幂函数变换的GM(1,1)模型得出的拟合值相差不大;从第11期开始,基于幂函数变换改进的GM(1,1)模型的精度较传统GM(1,1)模型有明显的提高。传统GM(1,1)模型的计算值平均误差为0.088 7 mm,预测中误差为0.097 3 mm;基于幂函数变换的GM(1,1)模型计算值平均误差为0.030 4 mm、预测中误差为0.059 3 mm。相较于传统GM(1,1)模型,改进模型预测平均误差仅有其34%,预测中误差仅有其60%,预测误差明显降低。由图3(b)可以看出,当预测至30期数据时,改进模型的预测值与原模型最大相差0.3 mm。 图3 第一组模型误差 原始观测数据见表3。 表3 原始观测数据 mm 根据第二组实验数据,利用传统GM(1,1)模型和基于幂函数变换的GM(1,1)模型分别进行拟合计算和预报计算,可以得到如图4、图5所示的结果。 图4 第二组两种模型拟合结果 图5 第二组两种模型预报结果 将两种模型计算出的结果进行统计(见表4)。 表4 第二组数据的预测精度对比 根据表4的误差结果,可以得到如图6(a)所示误差变化趋势。传统GM(1,1)模型的计算值平均误差为0.020 4 mm,预测中误差为0.149 7 mm;基于幂函数变换的GM(1,1)模型计算值平均误差为0.010 7 mm、预测中误差为0.142 5 mm。由图6(b)可以看出,针对第二组波动较大的数据,相较于传统GM(1,1)模型,改进模型预测平均误差仅有其52%,预测中误差为原函数模型的95%,预测误差明显降低。由此可见,改进模型适用性更好,预测精度更高。 图6 第二组两种模型的误差 (1)高速铁路施工沉降监测预报中,传统GM(1,1)模型在拟合和预报方面具有其局限性,当原始观测值波动较大时,会影响其预测精度。 (2)针对GM(1,1)模型拟合和预报时的不足,利用幂函数变换法将初始观测序列进行平滑处理,可提高GM(1,1)模型的拟合精度、预报精度。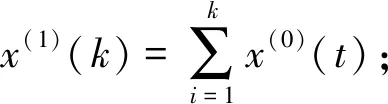
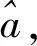
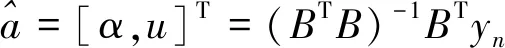
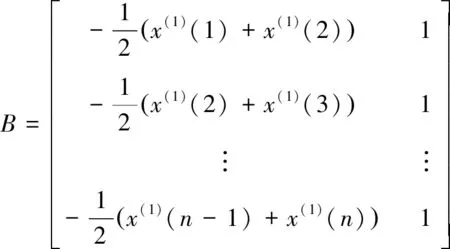
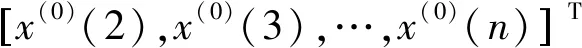
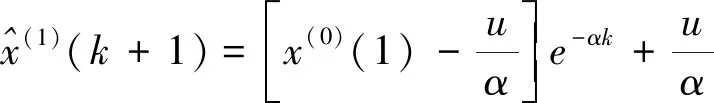
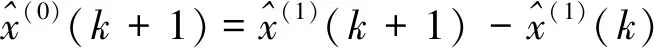
2 实验分析
2.1 第一组数据

2.2 第二组数据

3 结论
