冲击荷载下RC梁的力学性能研究进展
2020-08-06汪祥宇周锡武张文超
汪祥宇 周锡武 张 稳 张文超
(佛山科学技术学院,广东佛山 528000)
冲击是混凝土结构所受动荷载中一种较为危险的荷载形式,在冲击荷载作用下,会造成钢筋混凝土结构破坏乃至失效,从而导致人员伤亡和财产损失[1]。地震、海啸、泥石流、等自然灾害以及爆炸产生的冲击波、船撞桥、飞机失事撞击高楼、车辆撞击等人为灾害都属于冲击荷载造成损害的范畴。
冲击荷载下结构的动态力学性能与静态力学性存在较大的差异,受应变率效应、应力波效应、惯性力效应以及剪切效应的共同作用,钢筋混凝土结构的力学行为变得更加复杂[2-3]。目前的结构设计多以静态力学设计为主,对动力荷载一般采用经验法、等效静力法和扩大容许应力法等,但这些方法都难以精确的预测钢筋混凝土梁的抗冲击能力[4-6]。如何保障结构在强动力荷载下不被破坏,开展钢筋混凝土结构抗冲击性能的研究,是当前土木学科研究的重点。
动态响应和力学行为是梁体抗冲击性能的体现,目前,已有关于冲击力、支反力、惯性力、应变、挠度、裂缝开展、破坏模式,以及局部响应等方面的研究[9-12]。其中,很多学者把冲击力、支反力和挠度作为梁构件抗冲击承载力特征值的评价标准,然而,后续的研究者发现,三者在一定程度上可以体现梁的抗冲击性能,但作为抗冲击承载力的特征值并不准确[20-23]。
研究冲击荷载下梁的力学性能以及抗冲击设计是冲击力学实验最主要的目标,以下总结了大量研究者关于梁在冲击荷载下的理论与实验研究以及相关的数值模拟,并对研究者的研究结果进行讨论[57-59],以期对冲击作用下梁的力学性能研究寻找方向。
1 冲击作用下梁的四大效应
冲击荷载具有时程短、作用集中等特点,撞击体与梁接触过程中会产生明显的作用效应,包括应变率效应、应力波效应、惯性力效应、剪切效应,这些效应共同影响着梁在冲击荷载下的动态响应及力学行为。
1.1 应变率效应
应变率是指应变随时间的变化速率,也称为材料的率敏感性,是影响钢筋混凝土构件动态本构的重要因素。在冲击荷载下,须考虑梁体钢筋和混凝土两种材料的应变率效应。
早在1905年,Hopkinhon.B发现钢材在高应变率下的强度至少是低应变率下的2倍以上。Soroushian[1]对钢材的应变率效应进行了分析,认为钢材的弹性模量不受应变率变化的影响。另外有学者提出,钢筋类型对应变率的影响较小,反复加载下,钢材依然具有应变率效应,但进入强化阶段应变率效应就不明显,高温对材料的影响大于应变率对材料的影响[2-5]。
1917年,Abram[6]发现了混凝土的应变率效应。此后, Bischoff和perry[7]对混凝土动态受压进行了总结,认为在应变率增长界线内,混凝土的单轴抗压强度随应变率的增长而提高,其提高幅度主要取决于混凝土的静力强度和应变率。也有研究者发现,混凝土的受拉强度随应变率的增长而明显提高,应变率对弹性模量和泊松比没有影响[8-9]。欧洲混凝土协会(简称CEB)在2010年修正了动力加载下混凝土抗拉和抗压强度的应变率效应的计算公式[10]
抗拉:
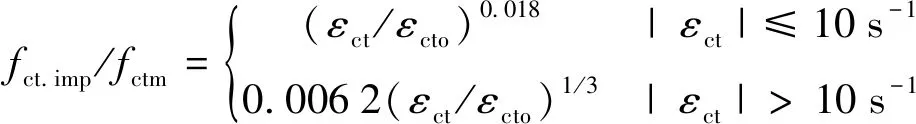
(1)
其中,fct.imp为动力加载时的混凝土抗拉强度,fctm为静力加载时的混凝土抗拉强度,εct为材料应变率,εcto为静力加载时的应变率值。适用范围为10-6~300 s-1。
抗压:
(2)
其中,fc.imp为动力加载时的混凝土抗压强度,fcm为静力加载时的混凝土抗压强度,εc为材料应变率,εco为静力加载时的应变率值。适用范围为-30×10-6~300 s-1。
在冲击荷载下,梁的应变率效应主要体现在梁锤接触区域的局部受压,梁底部纵向钢筋和混凝土的受拉,以及斜截面箍筋和混凝土的抗剪。
1.2 应力波效应
冲击应力波是应力和应变变化而引起的扰动以波的形式在固体中的传播,当载荷作用的时间与应力波传过物体特征尺寸的时间在同一数量级或更小时,需要考虑应力波的影响[11]。冲击荷载作用下,动荷载以能量的形式作用到梁上,除了冲击作用点耗能以外,其他能量均以应力波的形式向四周扩散,在梁短边和高度方向上由于距离较短,应力波作用时间可以忽略不计;在梁长度方向上,由于距离较远,应力波的作用时间较长,往往应力波还没传到梁支座,冲击力峰值已经出现,且应力波传播过程中,惯性力效应也随着应力波的传播向梁两端分布。若不考虑应力波的传播,对高速冲击作用下梁的力学性能分析将会产生严重偏差[12]。关于应力波效应和应变率效应的主要实验装置为霍普金森杆(如图1所示)。
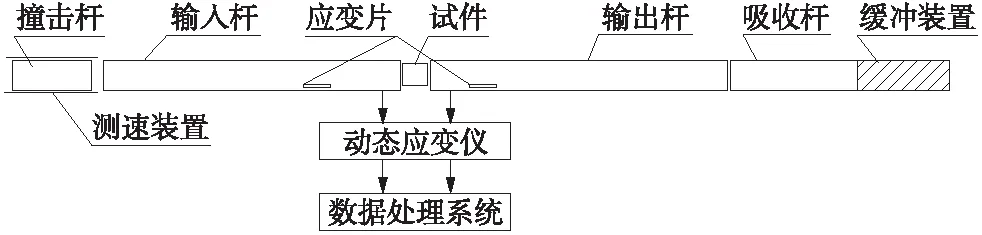
图1 分离式霍普金森实验装置
1.3 惯性力效应
惯性力效应是指冲击作用下,落锤的动能转化为梁体向下的加速度,进而产生向上的惯性力,惯性力也会影响梁的动态力学性能。Bentur[13]发现,在冲击力达到峰值时,惯性力占冲击力峰值的2/3以上。也有学者发现,冲击速度对结构的动态响应主要由梁体自身的惯性力所引起;在高速冲击下,结构的惯性效应占主导作用;在局部响应阶段,梁的冲击力完全由惯性力所抵抗,故梁的破坏损伤主要集中在局部响应阶段[14-16]。其影响过程为:在冲击开始时,荷载所传递的动能通过梁本身来储存和梁体损伤来消耗,这时惯性力效应发挥作用,惯性力随应力波向梁两端传播,储存的能量转化为梁体向下的加速度,使梁在净跨范围内向下移动,又通过梁体变形和裂缝展开来消耗,当梁体加速度为零时惯性力消失。
惯性力在梁长度方向上一般呈曲线或三角形分布,许斌和窦国钦[17-18]通过在梁体布置加速度传感器测得梁的加速度时程,加速度曲线如图2所示;赵武超和Thong M[19-20]采用数值模拟和经验公式推导,认为梁的剪切效应明显,在局部响应阶段梁沿长度方向惯性力分布如图3所示。
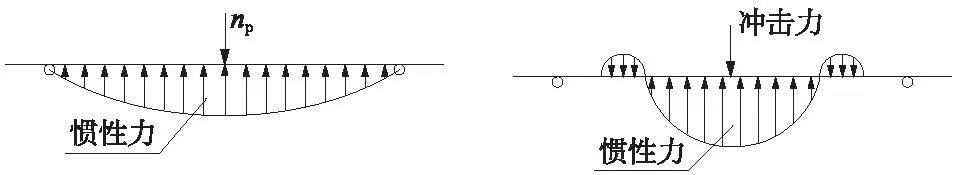
图2 惯性力呈曲线分布

图3 惯性力呈三角形分布
1.4 剪切效应
剪切效应是指在静载下发生弯曲破坏的梁,在冲击荷载下也有可能发生剪切破坏,梁所受到的弯矩和剪力随着加载形式的不同而发生改变。影响梁剪切效应的因素包括冲击速度、接触刚度、梁截面厚度以及梁净跨和悬臂长度等。剪切效应主要作用在梁的局部响应阶段,一方面,由于冲击荷载的瞬时特性,在局部响应还未结束之前,冲击荷载未能向梁两端传播,主要由冲击作用区域承担,梁所受到的剪力也集中在此区域,故易造成剪切破坏[21]。另一方面,跨度较小的梁在冲击荷载下会产生负向支座反力,且梁跨内会有反弯点的存在,这有效降低了梁所受到的弯矩,很大程度上提高了梁剪切破坏发生的可能[19]。因此,应提高梁构件的在冲击作用下的抗剪承载力,以满足可靠性要求。
总之,在梁的冲击试验中,四类效应共同影响着梁的动态响应及力学行为,在不同的实验工况中,这些效应影响效果的强弱也各不相同。
2 冲击荷载下梁的力学性能
动态响应和力学行为是梁冲击力学性能的体现,动态响应过程可分为局部响应阶段、整体响应阶段、回弹变形阶段[22]。局部响应阶段是梁发生破坏的主要阶段,整体响应阶段、回弹变形阶段主要体现梁的裂缝发展和位移变形。梁的力学行为包括梁冲击力、支反力、挠度等,可以定性以及定量的分析梁的冲击性能,可用于评估冲击荷载下梁的可靠性。
2.1 力学行为与冲击承载力特征值关系
梁的冲击力学行为可描述为冲击力、支反力、惯性力、应变、挠度等随时程变化,是梁在冲击荷载下最直观的力学性能体现,以下就力学行为与冲击承载力特征值关系进行总结探讨。
作为构件冲击作用最直观的定量表达,冲击力等效静载承载力已经运用到实际工程中,并提出了相应的冲击力计算公式[19,23,34],然而,通过实验发现,在冲击过程中,冲击力到达峰值时试件才开始发生位移,试件除局部外并未出现较大的损伤,冲击力转化为相应的惯性力和支反力,故用冲击力表达抗冲击承载力特征值并不准确[25]。
Soleimani[26]认为,钢筋混凝土梁在冲击荷载下的支座反力能间接真实地反映梁的截面弯矩。Kishi N[27]通过实验对比,发现采用支座反力比采用冲击力最大值更合理;许斌[28]通过落锤冲击试验,发现在冲击过程中,当支座反力达到第一个峰值时惯性力较大,且两者方向相反,支座反力有一部分被惯性力所平衡;当冲击速度到达一定值后,支反力不再随冲击速度的提高而增大[29]。故采用支座反力表达抗冲击承载力也不准确。
研究者们[30-32]还进行了大量梁的落锤冲击试验,通过采用残余挠度控制梁的破坏,得到了梁的抗冲击承载力的经验公式,但由于梁在冲击荷载下破坏状态复杂,且梁的破坏模式也会影响挠度变化,经验公式和容许挠度的定量相对保守。因此,采用残余挠度描述梁抗冲击承载力也不是一种合适的表述方式。
惯性力是梁体受冲击作用自身加速度的体现,在冲击过程中,支反力还未出现,冲击力完全转化为惯性力,此时达到惯性力峰值,梁体以最大的加速度下降,在惯性力消失时,梁体并未达到极限承载力[25],故采用惯性力表示梁的抗冲击承载力力特征值也不恰当。
钢筋应变达到屈服也是梁构件达到极限承载力的标志,由于局部破坏的影响,跨中受压区混凝土最先破坏,按照静载计算,其抗弯承载力显著降低,冲击速度越大,局部破坏越严重,钢筋屈服也相对延后,甚至梁破坏后,钢筋也未达到完全屈服[33]。因此,采用钢筋应变屈服极限表示梁的抗冲击力特征值也不准确。
尽管梁受冲击作用所得到的冲击力,支反力等作为梁的抗冲击承载力特征值并不恰当,但这些力学特征在一定程度上体现了梁的抗冲击能力。大量实验说明,冲击力峰值增大、惯性力峰值增大、支座反力峰值增大、钢筋屈服应变提高、跨中位移峰值减小,梁的抗冲击力也随之提高,关于梁的抗冲击承载力特征值的描述可以采用多因素共同控制,但其组合方式需要进一步深入研究。
2.2 梁的局部破坏
王明洋等[34-35]通过研究接触类型对局部破坏的影响,认为锤头类型、接触刚度对整体损伤的影响相对较小,但对局部损伤有较大的影响。余芳和付应乾[36-37]通过实验,发现冲击速度越大,梁的局部损伤越大。赵武超[47]认为只有在局部响应阶段梁不发生剪切破坏的前提下,才能保证整体响应阶段的弯曲破坏,同时局部响应阶段的损伤程度也会对整体响应阶段的承载能力产生影响。但局部响应阶段在瞬时发生,很难被捕捉,故该部分的内容须进一步研究。
钢筋混凝土梁破坏模式的改变主要与冲击速度,梁自身抗剪、抗弯能力以及剪切效应等有关。文献[38-40]进行了钢筋混凝土梁的落锤冲击试验研究,发现不同的冲击速度会导致不同的破坏模式。钢筋混凝土梁在低速冲击下发生弯曲破坏,而在高速冲击下却发生剪切破坏。文献[21,41,42]研究了箍筋配筋率变化对冲击破坏模式的影响,在冲击荷载作用下,无论梁发生剪切破坏还是弯曲破坏,剪切机制都发挥着重要作用;随着配箍率的增大,梁从剪切破坏向弯曲破坏转变,裂缝也会相应减少。文献[43-44]研究了纵筋配筋率对梁冲击破坏模式的影响,发现随着配筋率的提高,梁会由弯曲破坏向剪切破坏转变。
梁体裂缝可分为3部分:局部破坏产生的裂缝、底部受弯裂缝、剪切裂缝。局部破坏的程度以及破坏模式的转变对梁裂缝的开展具有重要影响。冲击荷载下,梁的裂缝多集中在碰撞区域,支座处一般为斜裂缝,且产生时间晚于碰撞区域[17,25,28]。
2.3 数值模拟以及理论分析
梁受到的动载作用为非线性,在数值模拟过程中,通常采用有限元LS-DYNA以及ABAQUS的显示算法来计算梁的冲击问题。目前,碰撞混凝土本构模型一般选用HJC模型以及弹塑性损伤帽盖模型[45-46],钢筋本构模型可采用双线性弹塑性以及弹塑性随动强化模型等。数值分析一般用于试验工况难以研究和相对繁杂的内容或对比实验结果是否准确,如赵武超[47]通过数值模拟,研究梁锤的接触刚度,锤头类型等对梁冲击力学性能的影响,并提出了损伤因子的概念;宋敏[43]在数值模拟中考虑了应变率效应,对高速冲击下梁的力学行为进行研究。
理论研究一般会涉及到碰撞模型的选择,Feldman[48]提出混凝土梁在冲击作用下抗弯计算的SDOF模型,被后续研究者[49]广泛用于分析冲击荷载下梁的动态响应以及梁在冲击荷载作用下的损伤评估。在此基础上,欧洲混凝土委员会(CEB)提出了单质点和双质点模型,但这几种模型均没有涉及应力波的传播以及惯性力效应。因此,在一些需要考虑惯性力效应以及应力波效应的实验中,该模型并不准确。
刚塑性模型也是碰撞理论计算的一种常见模型,将受冲击荷载的梁简化成理想刚塑性体,即忽略梁的弹性变形阶段以及应变强化效应和应变率效应。模型简化有一定的合理性,因为在冲击作用下,荷载所做的功大部分转化为梁的塑性变形能(在塑性变形阶段被消耗掉),而弹性变形只承受很少一部分荷载所做的功,对整体计算而言,忽略此部分能量并不会造成较大的误差,且大大简化了冲击过程中的数学以及物理计算[50]。在刚塑性模型运用的基础上,学者们又提出了塑性铰的概念:当梁所承受的弯矩大于或等于极限弯矩时,表明梁已经屈服,且梁跨内的曲率可以无限增大,相应的截面可以随意转动,像一个铰一样。塑性铰的形成和位置对梁的冲击力学行为有较大的影响[51]。但刚塑性模型在应变率效应明显以及弹性恢复力较大的构件中并不适用。
其他方面,宋春明等[52]对半无限粘弹性混凝土梁进行低速撞击试验,考虑了撞击对局部损伤的影响,建立了局部损伤与整体变形的关系式,推导梁在低速冲击下的撞击力和跨中挠度计算公式。王明洋[53]研究锤头形状对梁局部响应的影响,对梁在冲击破坏过程中的弹塑性和塑性阶段阶段建立冲击简化模型,得到梁在低速冲击下的计算公式。周泽平[54]推导出梁在冲击过程中所处的不同阶段的变形刚度,利用拉格朗日方程推导梁在弹性和塑性阶段的运动方程。李智[55]对冲击受损后梁的力学性能进行研究,拟合出冲击受损后梁的残余承载力和残余刚度公式。
3 梁抗冲击性能研究
梁的抗冲击性能是当前学者们研究的重点,也是梁构件承受动荷载抗力设计的主要目标。
Kishi[56]设计27根无腹筋混凝土梁的落锤冲击试验并提出了无腹筋梁抗剪计算公式
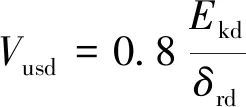
(3)
其中Vusd为梁静载抗剪承载力,Ekd为冲击能量,δrd为梁残余挠度。
Tachibana[57]对21根发生弯曲破坏的钢筋混凝土梁进行落锤冲击试验,提出了梁抗弯冲击力的经验公式
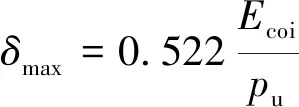
(4)
其中δmax为梁峰值挠度,Ecoi为冲击能量,Pu为梁静载抗弯承载力。
Kishi[58]为了得出基于性能的梁的抗冲击设计的经验公式,进行了钢筋混凝土梁的落锤冲击实验。研究表明:峰值挠度约为残余挠度的1.5倍(即Dmax=1.5δrs);并得到峰值挠度Dmax和残余挠度δrs关于冲击能量Ekd和梁静载抗弯承载力Pusd的两个抗冲击经验公式
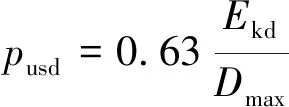
(5)
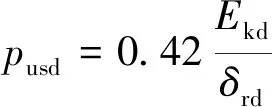
(6)
赵武超[19]在研究冲击荷载下梁的局部响应的同时,提出了梁截面内力计算公式
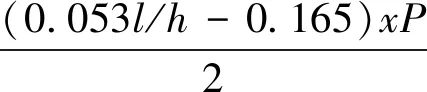
(7)
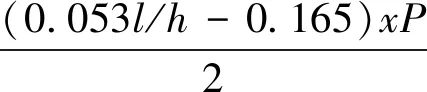
(8)
其中:P为冲击力;x为计算截面与支座之间的距离;a为悬臂长度;l为净跨长度;γ为负向支座反力合力与惯性力的比值。
在进行梁的抗冲击设计时,需要确定动荷载产生的弯矩和剪力分布。与静载不同的是,动荷载是关于时程的变化量,在不同的时程,动荷载影响梁的内力分布不同。图4是冲击作用前期(应力波未传至支座)不同学者[18,25,59]试验所得到梁的内力分布,此时梁主要受冲击力和惯性力作用。
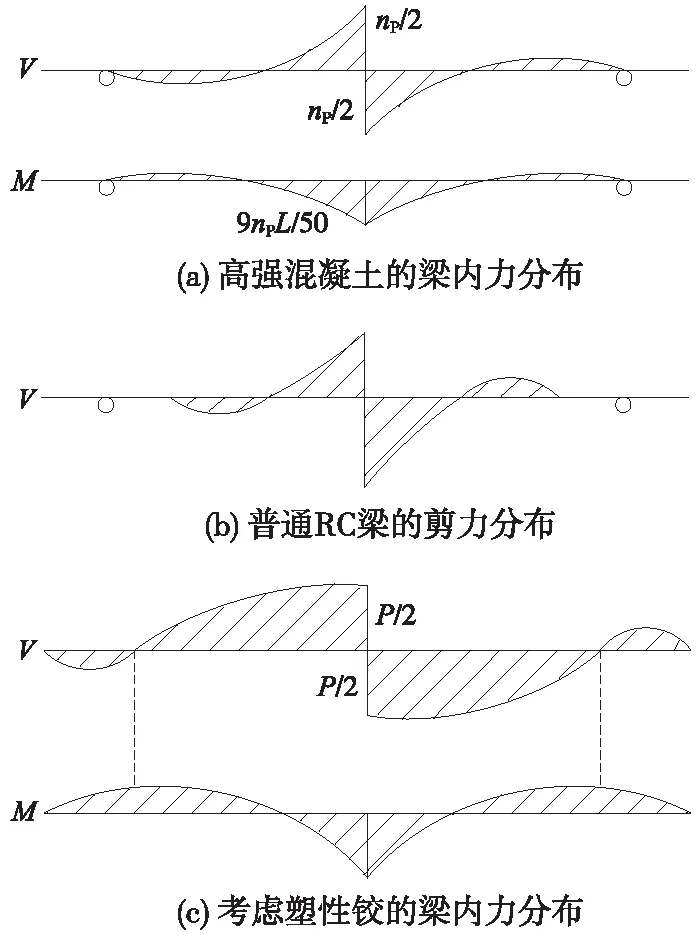
图4 冲击作用前期梁内力分布
由于动荷载作用下梁的力学行为非常复杂,梁的抗冲击能力的相关公式建立需要考虑局部响应、破坏模式,以及时程变化等因素,还需要学者们进行大量的实验及理论研究。
4 结论
(1)梁在冲击荷载下受四类效应的影响,在不同的实验工况下,四种效应对梁的动态性能的影响强弱不同,在实验过程中应抓住主要的效应,以提高冲击作用计算的准确性。
(2)冲击承载力特征值采用冲击力、支反力、挠度等因素表达有不恰当之处,但这些因素能在一定程度上反应梁的抗冲击能力。
(3)梁的局部响应对整体响应的影响很大,在实验中应加以考虑;梁的破坏模式受冲击速度、局部刚度以及梁的抗弯抗剪强度等多因素共同控制。
(4)根据冲击力以及挠度等建立的梁的抗冲击经验公式仅处于实验阶段,并没有太多的工程运用,且这些公式有一定的适用条件,其准确性也需要进一步验证。
