赏析临界法在解析几何中的运用
2020-08-05刘华荣
刘华荣
(江苏省泰州市姜堰区溱潼中学,225500)
解析几何的综合题是学生图形分析、推理演绎、数据处理以及交错运算的综合能力展示.而对于选择题或填空题无需呈现详细的解答过程,我们若能根据题型的特点选择精巧的方法,往往会让解题事半功倍.本文介绍的临界法就是解题中常用的巧法,意在寻找题干中满足某一几何特性的动态变化的对象,例如变化的点、线、三角形、圆等,根据其变化寻找相应的临界位置,找出满足题意的数量关系,使问题获解.下面笔者借助例题做一些浅陋的分析.
一、求离心率的取值范围
离心率问题是圆锥曲线题中频繁出现的问题,常见题型是圆锥曲线上存在一动点满足某一几何特性(比如角的大小、三角形的形状或其他数量关系),需要结合已知条件找出动点的运动与几何特性变化的关系,而临界法易于从动点的临界位置探索出其关键要素,使解题过程事半功倍.
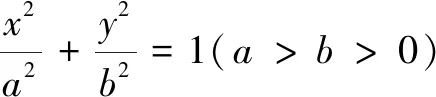
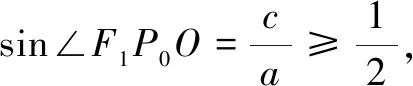

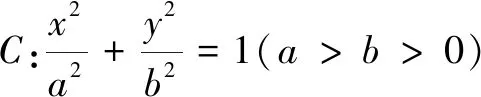
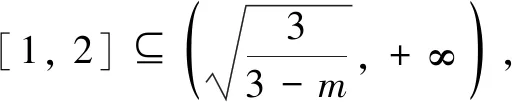
反思实际上,根据苏教版《数学(必修1)》中对于函数最值的定义,设函数y=f(x)的定义域为I,如果存在常数M满足:① 对于任意的x∈I,都有f(x)≤M;② 存在x0∈I,使f(x0)=M,那么M是函数y=f(x)的最大值(最小值类似可定义).所以,函数的最值问题实际上蕴含了不等式恒成立的思想,故可以采用类似不等式恒成立的方法通过寻找必要条件,利用定义域中某些特殊点的值,进一步缩小参数范围,简化解题过程.
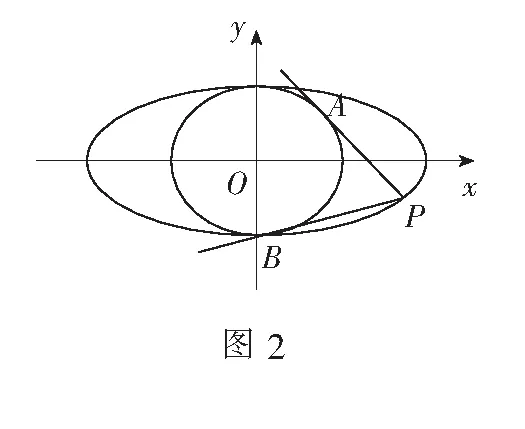
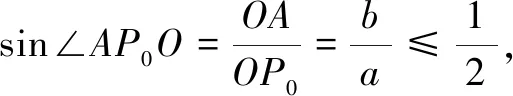
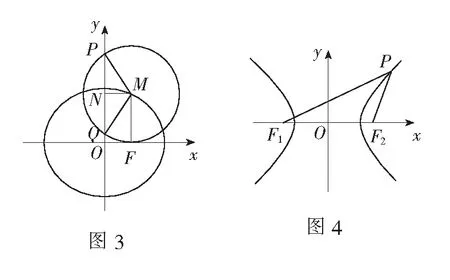
解∆PMQ是钝角三角形的临界情况为直角三角形. 如图3,过点M作MN垂直于y轴于点N,只要∠PMQ≥90°,即∠PMN≥45°即满足题意.
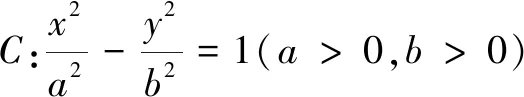

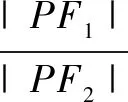
二、求值问题

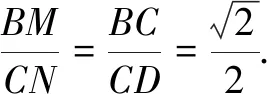
例4已知圆C:x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是______.


三、求参数的取值范围
例5已知直线l:3x+4y+a=0,圆C:(x-2)2+y2=2.若圆C上存在两个不同点P,Q,且直线l上存在点M,使得∠PMQ=90°,则实数a的取值范围是______.
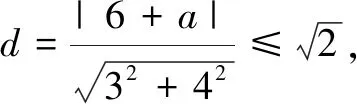
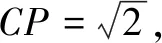
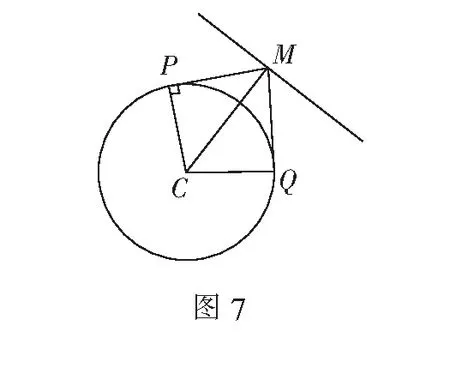
综上,实数a∈[-16,4].
通过以上实例分析,我们发现临界法在解几问题求解中屡建奇功,解题效率不容小视.
