挖掘必要条件 优化解题过程——例谈恒成立问题中的参数求值策略

王 颜 常国庆

(江苏省扬州市仙城中学225000) (江苏省扬州市新华中学，225009)

不等式恒成立问题作为近年来高考的热点题型,是高三复习课不等式部分的重点内容,其中不等式在某个定区间内恒成立是难点．对于这类问题,笔者发现学生热衷于“代入区间端点”解决问题,殊不知“代入端点”得到的条件只是原命题成立的必要条件,用来解题有失偏颇,很难得到正确答案．但是,是不是这样的解题过程就一无是处呢?正所谓“失败中孕育着成功”,笔者发现通过必要条件的挖掘,虽然不能严谨地得到答案,但完全可以优化解题过程．这个方法或许不是不等式恒成立问题一般意义上的通性通法,但是对于较为复杂的不等式恒成立问题或者函数最值问题来说,不失为一个打开思路的重要辅助工具．实际上,笔者认为,对于通性通法的认识应当是相对的,如果一个问题的“特性特法”被发现能够为一类问题的解决提供重要的解题思路,完全可以提升到通性通法的地位．下面通过几个例子说明问题．

例1(2008年江苏高考题)已知函数f(x)=ax3-3x+1,对于x∈[-1,1],总有f(x)≥0成立,则a=______.

分析要使f(x)≥0恒成立,只需使f(x)min≥0成立即可.通过导数求最小值,注意对参数a的讨论.

解法1f′(x)=3ax2-3.

(1)当a≤0时,有f′(x)<0恒成立,f(x)单调减.令f(1)≥0,得a≥2,舍去.

综上,a=4.

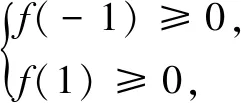
反思解法1是解决恒成立问题的通性通法,是基本方法,必须要掌握. 但在教学过程中,有学生使用解法2得到了,虽然不能求出a的值,但利用了恒成立的特点(即在一些特殊值处成立的必要条件)缩小了参数取值范围,并结合原有方法减少分类讨论的类别,简化了解题过程.

那么,特殊值的选择通常应当如何考虑呢?事实上,如下例2表明除考虑区间端点外,还可以考虑一些常见特殊值(如单调区间端点及0或±1等特殊点),进一步缩小参数取值范围.

例2设函数fn(x)=-xn+3ax+b(n∈N*,a，b∈R).

(1)若对任意x1，x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,求a的取值范围;

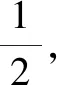
①

②

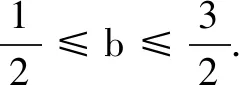
反思本题从必要条件所带来的结果中受益更大,不仅在题(1)中避免了通法引起的繁琐的讨论,而且给题(2)一个巧妙的解题思路.不过,由于必要条件自身的局限性,笔者觉得不能仅仅局限于代入端点,一定要在缩小参数范围的基础上,二度审视原题,确定最后的答案.

那么,这样的方法是不是只适用于不等式恒成立问题呢?能不能推广这种方法呢?下面,笔者想再通过两道函数最值的问题,再次说明这种方法的妙处.

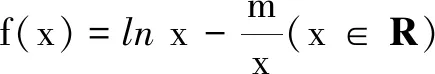
解法1若m≥0,则函数f(x)单调增,有f(1)=4,得m=-4(舍).

当-m<1,即m>-1时,f(x)在[1,e]单调增,有f(1)=4,得m=-4(舍)；当-m∈[1,e],即m∈[-e,-1]时,f(x)在[1,e]先减后增,f(-m)=4,得m=-e3(舍);当-m>e,即m<-e时,f(x)在[1,e]单调减,有f(e)=4,得m=-3e.

综上,m=-3e.

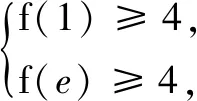
由此可跳过解法1的复杂分类讨论,直接得到f(x)在[1,e]单调减.由f(e)=4,迅速解决问题,得答案m=-3e.

例4已知函数f(x)=(m-3)x3+9x,若函数f(x)在区间[1, 2]的最大值为4,求m的值.

分析本题与例3类似,可通过对m分类讨论使问题获解,但解题过程较为繁杂.利用最值的定义，可得如下简便解法.