图象变换多维融合 数形结合凸显素养*——从2019年全国II卷理科第12题谈起

侯 军 卜大海

(中央民族大学附属中学海南陵水分校，572400) (广东省汕头市澄海苏北中学，515829)

在2019年的高考中,出现了一道以分段函数的为载体的图象多维变换问题,并在2020年的各类模拟试题中得到了广泛的拓展,形成了高考备考的新热点．本文对这一类问题进行探究和解读,希望对高三复习迎考有所帮助．

一、等间距伸缩变换

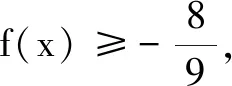
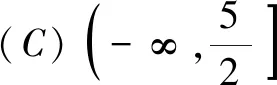
解依题意，因为f(x+1)=2f(x),所以f(x)=2f(x-1).

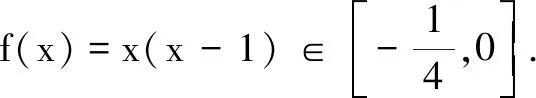
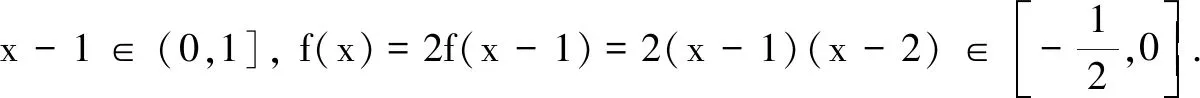
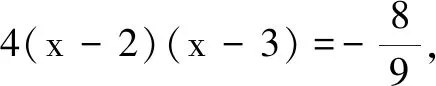
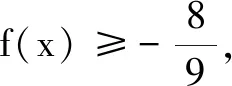
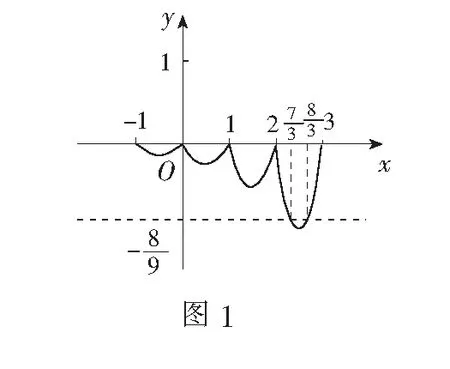
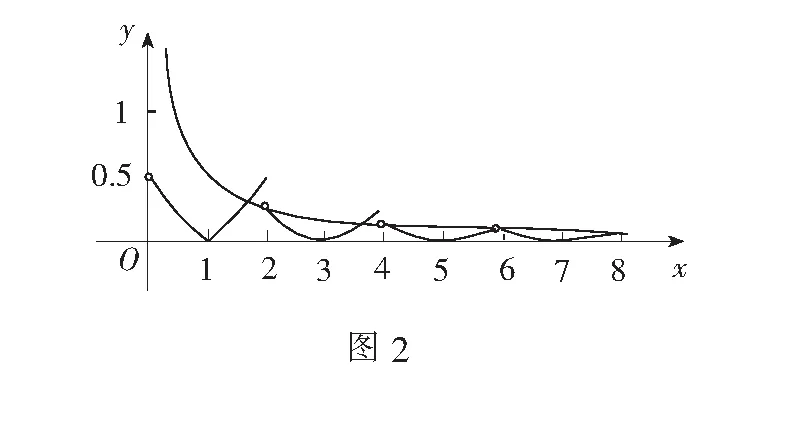
反思上述解法采用分类讨论、数形结合解决问题，做法耗时，且分段作图时易出错.我们考虑通过图象变换的方式达到快捷解题的目的．

更一般地,对于形如f(x+a)=bf(x)(a>0,b>0),可用如下两种形式快速作图.

方法1由f(x)=bf(x-a),其代数解释为:

x∈(x1,x2)时，f(x)=bf(x-a);

x∈(x1+a,x2+a]时，f(x)=b2f(x-2a);

…

x∈(x1+(n-1)a,x2+(n-1)a]时，f(x)=bnf(x-na).

其图形内涵是函数图象每向右移动a个单位,图象高度同时变为上一段图象的b倍．

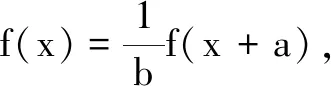
两种方法，本质相同.

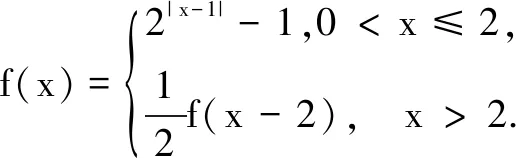
解当x=0时,易知g(0)=-1.

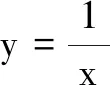
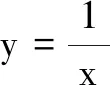
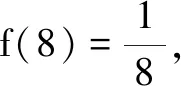
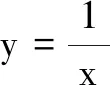
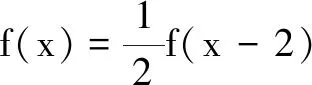
二、等间距平移变换

一般地,对于形如f(x)=f(x+a)(a>0)的函数f(x),可知f(x)以a为周期,其函数图象呈周期性重复,这类周期函数可视为函数已知段图象的等间距平移变换.

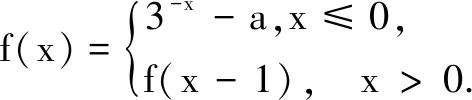
关于x的方程f(x)=x有且仅有两个不等实根,则实数a的取值范围是______.

解根据题意，当x≤0时,函数f(x)=3-x-a的图象是由y=3-x的图象向上或向下平移a个单位而得.

当x>0时,f(x)在[0,1]的图象是由f(x)在(-1,0]的图象右移一个单位得到;f(x)在(1,2]的图象是由f(x)在(0,1]的图象右移一个单位得到，…依此类推,可得到f(x)在y轴右边的各段图象,如图3所示.

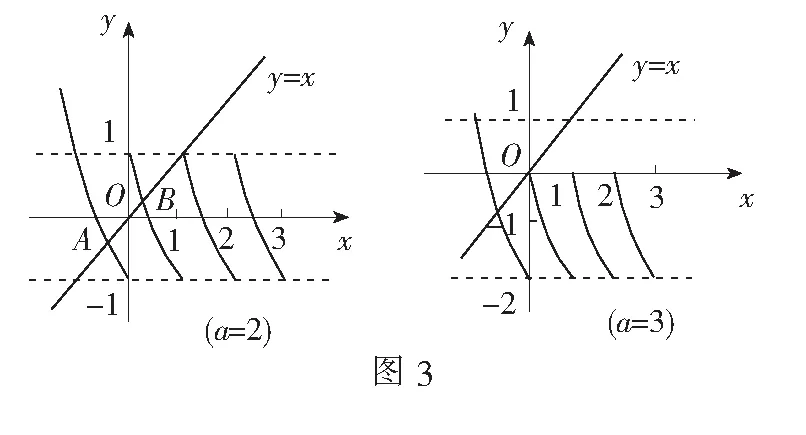
当a=2时,y=f(x)与y=x的图象恰好有且仅有两个交点.A,B.在此情况下，将函数y=f(x)图象向上微小平移一点,两图象就有三个不同的交点;向下平移一小段时,有两个交点,但向下平移超过一个单位(即a≥3)时,图象只有一个交点.

因此,当两个图象有且仅有两个交点时，a的取值范围为[2,3),此时方程f(x)=x有且仅有两个不等实根.

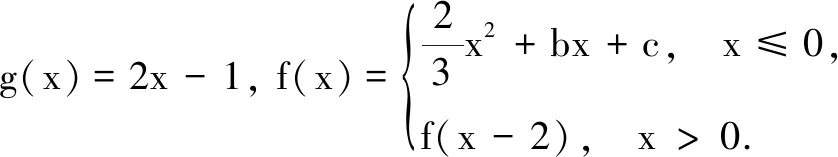
(A)2n+2 (B)2n2+n-1

(C)2n2+3n+1 (D)n2+4n+1

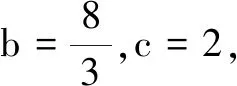
f(x)在(-2,+∞)的图象可由(-2,0]的图象向右以2为单位依次平移得到,如图5所示.

于是，f(x)在R上的所有零点为2k-3(k∈N),y=f[g(x)]在(-∞,2n](n∈N)上的零点为方程2x-1=2k-3(k∈N)的解,其中x≤2n.不难解得x=k-1(0≤k≤2n+1,k∈N),故所求零点之和为

评注本题有两个难点,一是函数图象的绘制,我们可以通过抛物线弧段等间距向右平移完成;二是对零点之和的求解,需由复合函数等价转化.事实上,作为选择题,还可以对n赋值,分析选项即可得到正确答案.

三、变间距伸缩变换

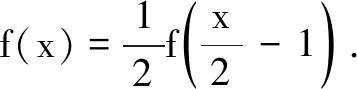
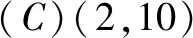
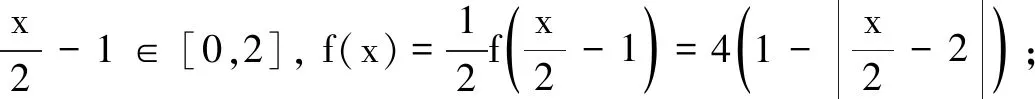
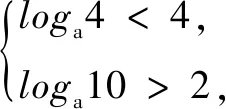
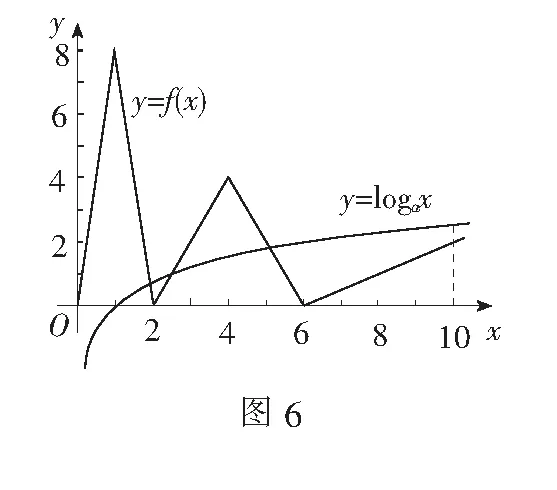
四、对称翻转变换

一般地,若函数f(x)满足f(x)=f(2a-x),则y=f(x)关于直线x=a对称;若函数f(x)满足f(x)+f(2a-x)=2b,则y=f(x)关于点(a,b)对称.这两个结论在分段函数中常有应用．

例6已知函数

关于x的方程f2(x)-af(x)=0有四个不同的实数解,则实数a的取值范围是______.

解由f2(x)-af(x)=0，可得f(x)=0或f(x)=a.

由f2(x)=af(x)恰有四个不同的实数