谐波齿轮柔轮中面曲线的几何特征拟合表达
2020-08-05邢静忠石立腾姚云鹏陈晓霞
邢静忠,石立腾,姚云鹏,陈晓霞
(天津工业大学 机械工程学院,天津 300387)
1 引 言
谐波齿轮是基于弹性变形原理发展起来的一种新型的机械传动装置,其中波发生器使柔轮产生可控的弹性变形并与刚轮啮合实现运动和力的传递。谐波减速器具有传动比大、传动精度高、回差小等优点被广泛应用于机器人、雷达及航空航天等精密传动领域[1-3]。谐波齿轮独特的工作原理使其传动精度、负载能力与轮齿齿廓、柔轮变形密切相关。齿圈中面曲线的准确表达[4-5]是齿廓设计的基础,对谐波齿轮的研究至关重要。
谐波齿轮传动装置的创始人Musser在进行齿廓设计时仅把柔轮中面曲线(中性线)变形考虑为沿径向的移动,未考虑周向移动和法线转动[1]。目前对计算截面上柔轮中面曲线变形普遍采用基于力学小变形假定下的圆环理论以径向位移、周向位移和法线转角来表达[6],这种方法对柔轮变形进行了全面分解,是一种较为准确地近似计算方法。
陈晓霞等[7]提出一种基于柔轮装配变形的共轭精确算法,用于求解周向位移引起的转角以及齿廓对称线相对于径矢的转角。为进一步描述柔轮变形,Chen等[8]基于胡克定律提出由周向力引起的周向伸长对中面曲线变形的影响。Dong等[9]通过双三次样条函数对有限元接触分析模型所得柔轮变形离散数据进行拟合得出变形函数。杨勇等[10]提出一种基于柔轮弹性变形和运动学关系的共轭精确算法,用于求解椭圆波发生器作用下柔轮中面曲线的变形函数。Ma等[11]提出一种研究驱动速度对柔轮变形特性影响的试验方法,为柔轮变形在运动学方面的研究提供了实验依据。
上述研究中对柔轮变形的研究分别基于圆环理论、有限元分析和实验。通过把变形分解为径向位移、周向位移和法线转角进行求解,叠加在变形前的模型上表示最终形状。此类方法虽然简化了计算,但是忽略了力学小变形假定带来的误差。并且叠加顺序不同也将对极角结果产生不同的影响。
凸轮类波发生器是目前应用最普遍的一种结构形式。现有计算理论求解获得的双偏心圆弧凸轮波发生器作用下的圆环在包角内的中面曲线曲率半径并非恒值。这种显然与自身模型相矛盾的现象,主要源于曲率计算应用了近似公式。已有研究[8]还发现:现有理论计算中的中面曲线存在远大于实际的周向伸长。这两种情况下径向和周向位置的近似表达,会显著影响后续齿廓设计和啮合性能评价。
柔轮齿圈中面曲线变形前为圆环,在双偏心圆弧凸轮波发生器作用下,柔轮中面曲线在长轴处固定,在短轴处所受力和弯矩的作用下中面曲线逐渐紧密贴合在理论计算圆弧上形成一定包角的接触区。柔轮变形量相对于齿圈壁厚属于大变形问题范畴,且涉及接触力学问题。在包角较大时,大多数工程结构问题中普遍采用的线性能量法显现出局限性。力学大变形求解复杂且有限元大变形求解也需耗费大量机时。因此,本文将变形贴合过程分解为两段分别处理,包角内按照等距线直接固定在凸轮上,其中包角为未知量,只保留包角外的变形段进行小变形研究。通过基于变形后的形状在端点处的斜率和曲率条件,采用多项式曲线来拟合中面曲线。并基于变形后中面曲线的长度变化,获得其在包角外的曲线形状。
2 谐波齿轮柔轮变形模型
在未装配时,柔轮齿圈中面曲线是以O2为圆心,rm为半径的圆弧AC(虚线);在装配凸轮后,圆弧段AC发生变形,分为接触区CB′和非接触区B′A′(如图1)。柔轮变形后的回转中心为O1,接触区圆弧CB′(实线)紧贴在以O3为圆心R为半径的波发生器理论计算圆弧上;非接触区为光滑曲线B′A′段(实线);e为圆弧的偏心距;u0为柔轮长轴处的最大径向位移;γ为柔轮关于O1对波发生器的包角;φ为以y轴为起始关于O1的极角;M1和N1分别为柔轮中面曲线A′处的弯矩和周向力,由柔轮变形的对称性可得,A′处的剪力为零。
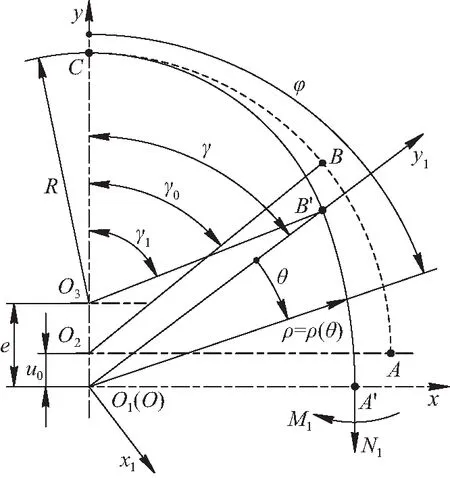
图1 柔轮中面曲线变形图Fig.1 Deformation diagram of flexspline neutral line
2.1 柔轮变形模型各参数的关系
根据谐波齿轮传动装置的结构特征,波发生器理论计算圆弧的半径为R=R1+sc+s1/2,其中R1为圆弧半径,sc为衬环厚度,s1为柔轮齿圈厚度;偏心距为e=rm+u0-R。依据弧长条件,包角γ转换到未装配时圆弧AC上,所对应的包角为:
γ0=γ1R/rm.
(1)
根据图1的几何关系,接触区圆弧CB′段在圆弧上所围弧度为:
γ1=γ+arcsin[(esinγ)/R],
(2)
则接触区CB′弧长为:
CB′=γ1R.
(3)
在平面直角坐标系O1-xy中,设点B′的坐标为 (xB′,yB′),根据几何关系可知:
xB′=Rsinγ1,yB′=e+Rcosγ1.
(4)
3 柔轮中面曲线变形函数
如前所述,现有的理论计算方法不能保证足够的求解精度。为尽可能地准确求解出包角以及柔轮中面曲线变形后的几何形状,采用几何学方法对力学小变形假设理论表达的柔轮变形进行几何特征拟合。以O1为坐标原点,O1B′所在直线为y1轴建立平面直角坐标系O-x1y1如图1所示。
3.1 接触区变形函数
由图1可知,接触区CB′段的函数:
x2+(y-e)2=R2,x∈[0,xB′],
(5)
式中xB′为关于包角γ的函数。在该几何特征拟合表达法中包角γ为未知量,需要和后续非接触区变形函数表达式进行联立求解。
3.2 非接触区变形函数
依据图1可知,接触区CB′圆弧段和非接触区B′A′曲线段在平面直角坐标系O1-xy中的极角范围分别为0≤φ≤γ和γ≤φ≤π/2,其中φ角的起始点在y轴上方向如图1所示。由于柔轮齿圈中面曲线非接触区B′A′段为光滑曲线且满足一定的约束条件,为了方便数学模型建立和求解,故设该曲线段的表达式在平面直角坐标系O-x1y1中为极坐标形式的多项式函数。其中θ角的起始点在y1轴上的方向如图1所示,记作η=π/2-γ,则极坐标形式的多项式函数为:
(6)
依据图1的几何关系和波发生器类型,可得非接触区B′A′曲线段的6个几何约束条件:B′处的连续性条件;B′处的光滑(斜率)条件;B′处的曲率条件;A′处的斜率条件;A′处的曲率条件;非接触区的弧长条件。
为了唯一确定式(6)中的系数,约束方程个数应等于未知量的个数。由于包角γ为未知量,故只能确定式(6)中的5个系数,即n=4。根据式(6),可得非接触区极坐标形式的多项式函数如式(7)所示:
(7)
式(7)关于θ的一阶、二阶导数分别为:
(8)
(9)
对上述6个约束条件分别建立约束方程:
(1)B′处的连续性条件
根据连续性条件,点B′为接触区与非接触区的分界点,即点B′在式(7)和式(4)中的坐标位置相同:
(10)
根据式(10)和图1中的几何关系有:
(11)
(2)B′处的光滑(斜率)条件
由于在双偏心圆弧凸轮波发生器的作用下,接触区CB′圆弧段与非接触区B′A′段在点B′处光滑连接。可知两曲线段在点B′处的斜率相等,即k1=k2。根据图1的几何关系,在坐标系O-x1y1中接触区CB′段在点B′处的斜率为k1=-tan(γ1-γ);非接触区B′A′段在B′处的斜率为k2,则依据式(7)可得:
(12)
式中,x1=ρsinθ,y1=ρcosθ。
在θ=0时,联立式(7)、式(8)和式(12)可得:
C1=-C0tan(γ1-γ).
(13)
(3)B′处的曲率条件
由于接触区CB′段半径为R,其曲率半径为R1,则R1=R;非接触区B′A′段在B′处的曲率半径为R2。根据柔轮齿圈中面曲线变形特征两曲线段在点B′处的曲率半径相等,即R1=R2。B′A′段在式(7)表达下,其任意位置的曲率半径:
(14)
依据式(9)可得,ρ″(0)=2C2,则点B′处的曲率半径为:
(15)
由式(15)可得:
(16)
(4)A′处的斜率条件
根据柔轮齿圈中面曲线变形特征整个齿圈中面曲线为光滑连续的曲线,点A′处于短轴处,则该点处的切线与x轴垂直。根据图1,在坐标系O-x1y1中点A′处的斜率kA′=-1/tanγ,则式(7)所求该点处的斜率:
(17)
由式(17)得:
(18)
(5)A′处的曲率条件
由于柔轮中面曲线变形问题属于力学大变形和接触问题,对于变形后短轴处点A′的精确位置求解相当复杂,故对该点处做近似处理。为减小近似处理带来的误差,取力学小变形假定条件下短轴处的曲率作为约束条件。
力学小变形假设条件下的位移叠加表达法对柔轮齿圈中面曲线的变形计算,通常取u0,rm和R为已知量,包角γs为未知量。由式(19)求解包角γs,即:
(19)
式中:A1=η1-sinγscosγs,B1=(4/π)(cosγs-η1sinγs),η1=π/2-γs。
在位移叠加表达法中柔轮齿圈中面曲线非接触区在极角φ处的径向位移u(φ)和极径ρ1分别为:
(20)
ρ1=ρ1(φ)=rm+u(φ).
(21)
式(21)关于φ的一阶、二阶导数分别为:
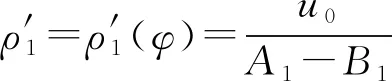
(22)

(23)
在极角φ=π/2的点A′处,通过位移叠加表达法求得曲率半径为:
(24)
非接触区B′A′段在极坐标形式的式(7)表达下,由式(14)求得在点A′(即坐标系O-x1y1中θ=π/2-γ)处的曲率半径为:
(25)
式中:A2=[ρ2(η)+ρ′2(η)]3/2,B2=ρ2(η)+2ρ′2(η)-ρ(η)ρ″(η)。
综上可知,式(11)、式(13)、式(16)、式(18)和式(25)均为关于包角γ的函数。将式(11)、式(13)、式(16)和式(18)代入式(25)可得只含未知量C4和包角γ的非线性方程,记为:
C4=g(γ).
(26)
(6)非接触区的弧长条件
在坐标系O-x1y1中非接触区B′A′段弧长由多项式函数式(7)求解得:
(27)
基于柔轮齿圈中面曲线变形前后伸长条件,四分之一模型中柔轮中面曲线总伸长量ΔS为[3]:
(28)
联立式(3)、式(27)和式(28)得,
(29)
式(29)为含未知量C4和包角γ的非线性方程。
联立式(26)和式(29),以包角γ为迭代变量,通过迭代进行求解。由式(19)求出小变形假设条件下的包角γs,可以缩小迭代包角γ取值范围,进而减少所需迭代次数。
4 模型求解与验证
4.1 双偏心圆弧凸轮波发生器和圆环接触模型
为减少模型参数对求解结果的影响,采用控制变量法选取算例,依据式(19)把柔轮齿圈中面曲线半径和最大径向位移设置为定值,改变圆弧的计算半径从而产生不同包角的模型。本文选取15个波发生器作用下的算例如表1所示。中面曲线半径rm= 61.7 mm,最大径向位移u0=0.7 mm,柔轮齿圈厚度s1=1.4 mm。

表1 不同包角的算例参数Tab.1 Illustration parameters under different wrap angles
4.2 几何特征拟合法对模型求解
依据表1中各算例的参数(除小变形理论包角γs以外)联立式(26)和式(29)进行迭代求解,结果如表2所示,其中中面曲线弧长迭代误差限ε=1×10-6。
4.3 有限元模型验证
由本文所研究对象为柔轮齿圈理论计算截面中面曲线变形属于平面问题,在ANSYS中建立齿圈和波发生器的有限元分析接触模型,通过设置位移载荷使该有限元模型属于平面变形没有锥度的变化并分别打开大变形和小变形开关进行求解。提取各算例在有限元分析(Finite Element Amalysis,FEA)模型中柔轮齿圈的接触比压,选取接触比压的波峰所在的极角作为模型的包角与理论解进行对比分析。
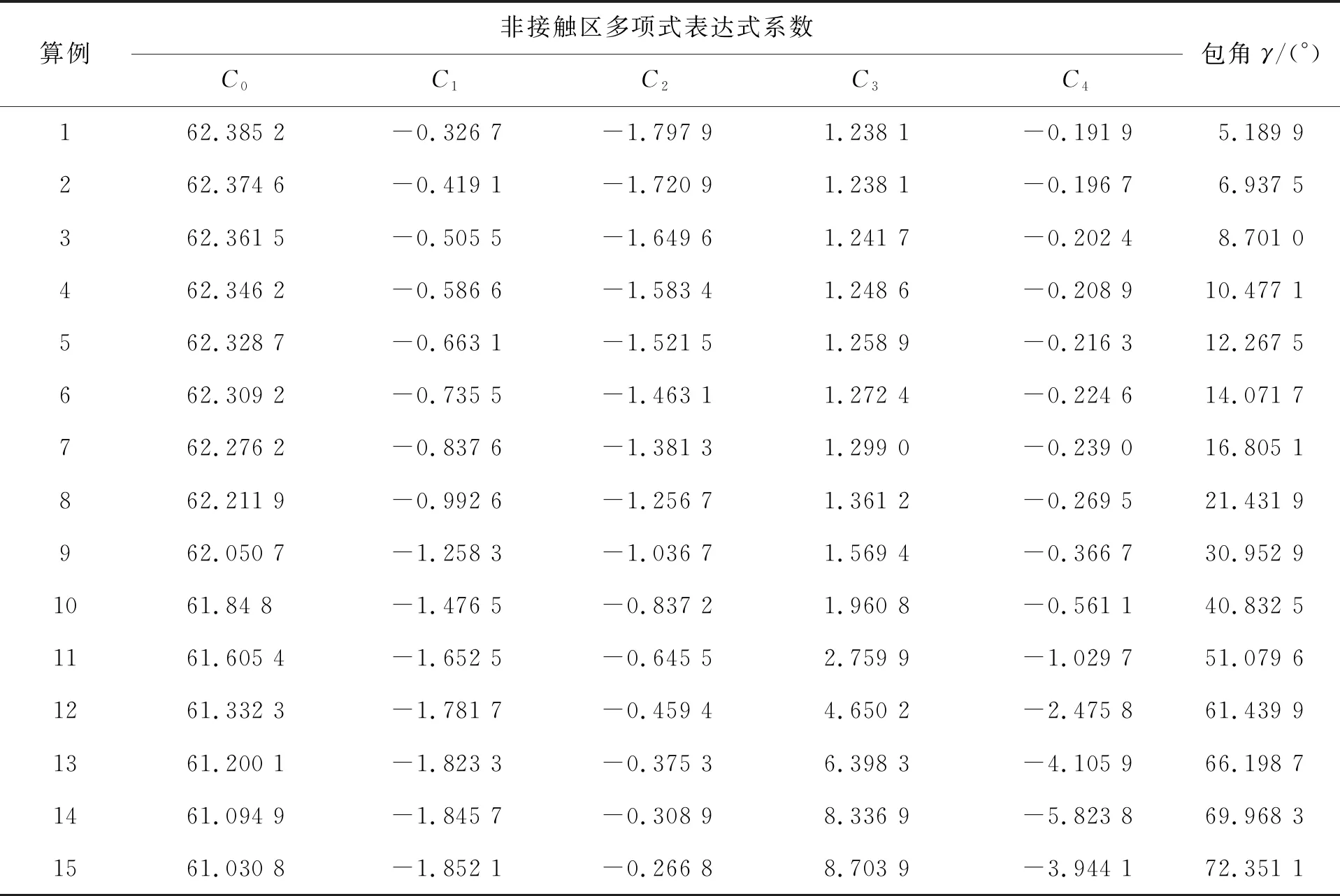
表2 不同包角算例的计算结果Tab.2 Results under the specified wrap angles
力学小变形理论的位移叠加表达解和FEA解中的极角是相对于变形前的柔轮回转中心O2如图1所示,为了方便进行比较对本文方法求解的包角γ由式(1)和式(2)转换为γ0。
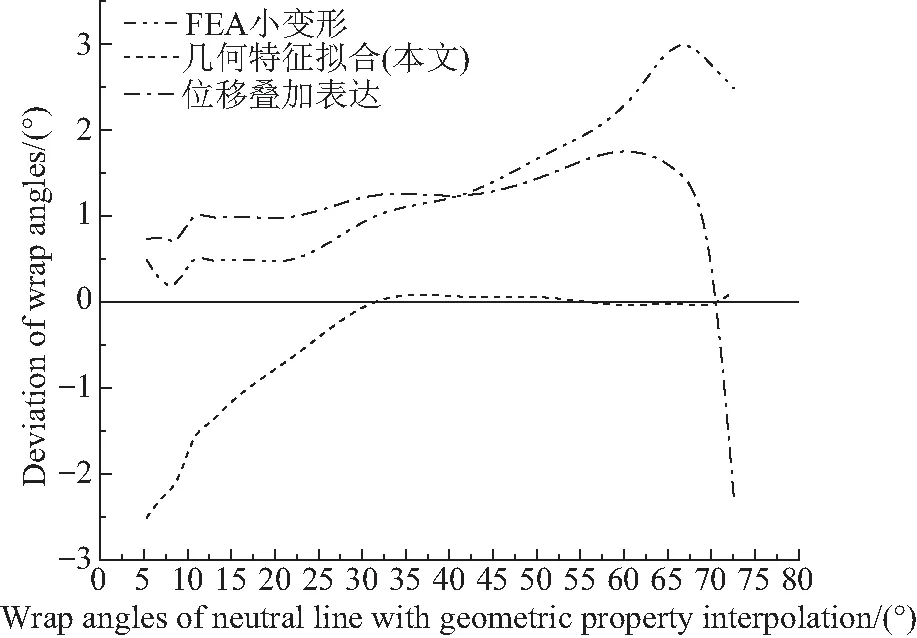
图2 不同模型在4种求解方法下所求包角Fig.2 Wrap angles of different models from four methods
由于柔轮的变形属于大变形接触问题,相比于其他小变形理论FEA大变形结果更接近实际,以其求解结果作为分析基准。为了比较直观地反应不同理论求解的差异,对FEA大变形所求包角与其它方法所求包角做差如图2所示,其中横坐标表示本文方法所求不同模型的包角。
从图2可知,随着模型包角的增大,位移叠加表达法的理论结果和FEA小变形的数值结果与FEA大变形的偏差越来越大。而本文方法的结果和FEA大变形的结果基本相同;在模型包角小于25°左右时位移叠加表达法和FEA小变形结果所求包角偏差分别稳定在1°和0.5°左右,而本文方法在此范围内具有显著偏差。
由于各算例下中面曲线变形后长轴长相等,为了进一步分析和验证各种理论方法适用性,对各模型在不同计算方法下的中面曲线变形后的短轴长进行分析比较,求解结果如图3所示。其中横坐标表示本文方法所求不同模型的包角。
由图3看出,随着模型包角的增大,短轴极径的FEA小变形解和位移叠加表达法解与FEA大变形的结果偏差越来越大;本文方法的结果在模型包角约小于65°时与FEA大变形的偏差随模型包角的增大而减小,且包角在25°~65°之间的模型的结果与FEA大变形结果基本相同。
由于谐波减速器属于精密传动装置,有必要对小变形理论假设下的位移叠加表达法引起的轮齿定位偏差进行分析。

图3 不同模型在4种求解方法下所求短轴长度Fig.3 Short axis sizes of different models from four methods
4.4 柔轮轮齿定位参数偏差分析
目前对柔轮轮齿的定位普遍采用变形后的柔轮齿圈中面曲线与轮齿对称线的交点作为定位点[12-14]。在上述方法的基础上对FEA大变形、FEA小变形、位移叠加表达法和本文方法的轮齿定位精度进行对比分析。对变形前的齿圈中面曲线圆环以等弧长进行等分选取定位点[15],按照位置参数极角和极径,分别对上述4种方法下各个轮齿定位点在变形后的位置进行比较。由上述分析可知,本文方法在模型包角在25°~65°时具有较高求解精度。
最低装配应力的最合理包角为20.72°[3]。这里选择30°包角为例,验证本文算法给出的定位参数:极角(如图4)和极径(如图5)。并以FEA大变形为基准与其他方法求解的轮齿定位参数做差,横轴是变形前圆环上轮齿定位点的极角坐标。
由图4看出,4种方法在短轴和长轴处轮齿定位极角几乎没有偏差,其中本文方法的结果在整个区间偏差几乎为零;FEA小变形在包角内的偏差小于0.001°,随着变形前定位点极角的增大,在62.5°左右时偏差达到最大值约为0.004°;位移叠加表达法结果在20°左右时达到包角内偏差最大值约为0.001 6°,极角坐标为65°左右时达到整个区间偏差的最大值约为0.005 8°。
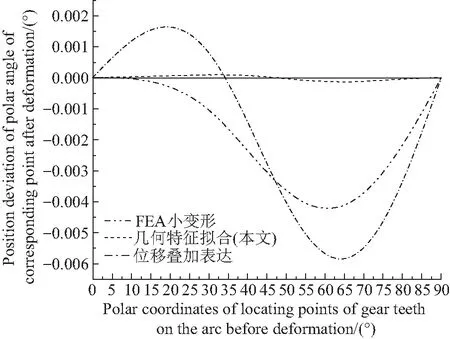
图4 4种方法给出的包角30°算例的极角Fig.4 Polar angles of the 30° wrap angle example in four methods
从图5可以看出,在包角内FEA小变形和本文方法所求极径偏差几乎为0,位移叠加表达法极径偏差最大并随极角的增大而增大;在包角外本文方法结果偏差相对稳定且小于0.001 mm,而FEA小变形和位移叠加表达法极径的偏差随极角坐标的增大而增大,在短轴处极径偏差达到最大值。

图5 4种方法给出的包角30°算例的极径Fig.5 Radial length of 30° wrap angle example in four methods
5 结 论
提出基于变形后的形状对装配状态下理论计算截面柔轮齿圈中面曲线变形进行表达,推导出接触区和非接触区变形函数表达式,并解出包角。模型包角约小于25°时小变形理论假设下的位移叠加表达法具有较高求的求解精度;在模型包角在25°~65°之间时本文方法与FEA大变形结果基本相同,具有较高的求解精度。相比位移叠加表达法的计算结果,在模型包角为30°算例中本文方法求解的极角偏差降低了约0.006°,极径偏差降低了约0.013 mm。
