可见光通信网络节能资源分配策略研究

徐文艳，唐 涛，段田东，杨 森

(战略支援部队信息工程大学，河南 郑州 450001)

1 引 言

近年来，可见光通信[1](Visible Light Communication， VLC)由于其未授权频谱、高效节能照明等特点，发展迅猛。VLC是一种使用高能效的发光二极管(Light Emitting Diode，LED)[2]作为发射机，向用户发射光和信息信号的通信系统，可用于通信消耗的电力也可用于照明，因此VLC网络也被认为是一种节能技术[3]。然而其信息信号的功率必须满足照明要求的范围，并且在LED的物理极限范围内[4]，这就要求在保证QoS的前提下，尽可能地减少通信所消耗的额外电能，以提高系统的能源效率(Energy Efficiency， EE)。而且5G网络需要大量的光接入点(Access Points， APs)和连接设备，设计节能系统的需求变得更加迫切[5]。

当用户随机分布时，室内VLC网络中的每个用户在特定位置可能会接收到来自多个光APs的视距信号，这些信号相互叠加，小区边缘的小区间干扰(Inter-cell Interference，ICI)严重，小区间干扰[6]是降低EE的主要原因。因此提出将多个APs分组到一个光小区中协作传输缓解小区间干扰问题。在高度密集的VLC网络中，当用户数量远小于APs数量时，以用户为中心的VLC网络架构设计是一种合适的小区形成技术[7]。文献[8]研究了VLC的以用户为中心的设计原则，由此产生的用户到网络的关联结构是基于非常规形状的。系统首先聚集用户，然后将APs与分组的用户相关联。文献[9]提出了不同VLC协作传输模式最优用户关联集中式方法和离散线性规划逼近方法。VLC/WiFi混合网络中[10]的切换决策过程中也应用了对偶梯度法。但是为了减少AP选择的复杂性，接收者只能在独立的VLC或WiFi网络中选择链路数据率最高的AP，上述研究均忽略了功率分配对VLC网络的影响，可能会降低系统性能。实际上，功率分配可以缓解网络中用户间的干扰，使总速率效用、比例公平效用和最小速率效用等最大化。文献[11]扩展了工作以增强用户之间的公平性。文献[12]为小区用户分配了功率，目的是最大化分布式小区的EE。以往的大部分研究[13-16]都是针对高效节能VLC系统的系统级优化，分别解决了小区形成和功率分配的问题，但它们是相互联系的问题。在射频(Radio Frequency，RF)网络中，在联合用户关联和功率分配方面已经开展一些工作，文献[17]研究了一种联合功率控制和负载感知的用户关联算法，实现宏小区到微小区的流量分流以及小区间的干扰缓解。文献[18]考虑了蜂窝网络中传输功率、用户调度和用户关联的联合优化，以基于干扰定价方法最大化加权平均。文献[19]提出了一种联合用户关联和干扰管理算法，用于大规模的多输入多输出(Mulitple-input Multiple-output，MIMO)网络中。然而功率分配问题通常是非凸的甚至是NP-hard[20]问题，因此很难获得全局最优解[21]。

本文针对以用户为中心的VLC系统，提出了一种新的高效算法来设计节能的VLC网络，用户在接收机的视场角(Field of View，FOV)范围内的任何地方都可以动态关联Aps，为了提高系统性能，同时研究VLC网络中功率分配与用户关联问题，为了简化问题，本文独立实现了用户的聚类过程，并联合实现Aps选择和功率分配问题。提出了一种新的用户聚类算法，引入BWP(Between-Within Proportion)聚类有效指标，该算法的目标是最小化用户到小区中心的距离以及最大化不同小区间用户的平均距离，不仅能确定最优聚类数目而且减少小区间的干扰。其次为每个AP建立一个度量值，以选择AP关联的合适用户集群。最后，针对功率分配和APs选择的联合问题，提出了一种低复杂度的解决方案，目的是在可接受的EE性能下降的情况下降低计算的复杂度。数值结果表明，在给定的用户聚类和AP关联算法下，存在最优的聚类数量以获得较高的EE。

2 系统模型

假设室内系统由一组NAVLC Aps和Nu用户组成，使用脉冲幅度调制(Pulse Amplitude Modulation， PAM)作为调制方式。如图1所示，用户均匀地分布在房间内，APs固定在房间天花板上。每个VLC AP都配备了多个LED，通过强度调制 (Intensity Modulation，IM)将光信号传输给用户，用户通过光电探测器(Photo Detector， PD)接收信号，同时假设用户在短时间内保持不变，因此VLC链路的信道状态信息(Channel State Information，CSI)在此期间被认为是恒定的。假设用户数量远小于APs数量，本节中主要研究如何构建以用户为中心的光小区。

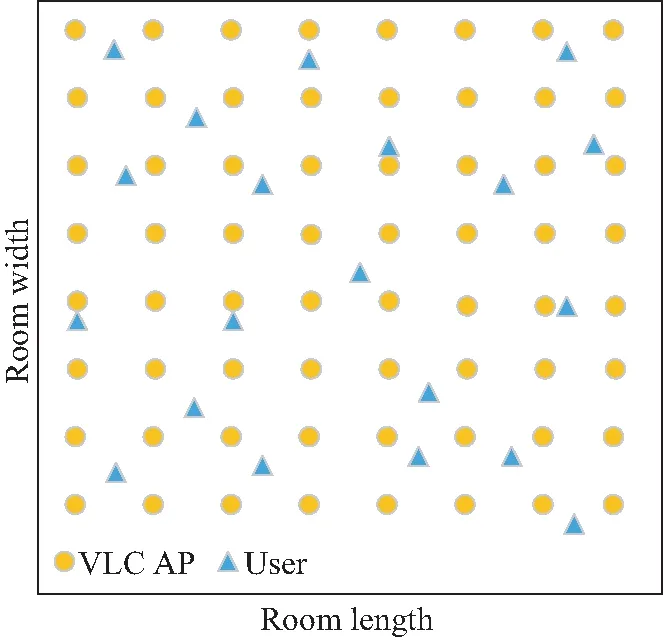
图1 室内VLC AP布局以及用户在水平面投影示例Fig.1 Indoor VLC AP layout and user level projection

2.1 光高斯信道模型

假设室内可见光通信系统中发光二极管(LED)符合朗伯光源模型，则用户i和APj之间的直射信道的直流增益[22]可以表示为：

(1)

其中：m为朗伯辐射阶数，m=-ln2/ln(cosφ1/2)，φ1/2是半功率角，APD为用户等效接收面积，d为光AP到用户接收机之间的距离，φ为LED灯光的发射角，ψ为光信号在LED发射光线的入射角，ψFOV为光接收机的视场角，Ts(ψ)是光学滤波器增 益，g(ψ)是聚光器增益，用式(2)来表示：

(2)

其中κ为折射率。

VLC系统中，采用IM/DD方案对信号调制和检测，发射信号必须是实值而且是非负的，考虑用眼安全，信号也要受到平均光功率的限制。因此，在VLC系统中不能简单地使用射频系统中经典的香农公式。在VLC系统中IM/DD信道通常被建模为加性高斯白噪声信道[23]，但是针对输入信号幅度的约束，目前信道容量还没有精确封闭表达式，只能用几个紧容量边界接近信道容量。信道容量近似用下界来表示[24]：

(3)

其中：ω是常量，ω=e/2π，ρ是光电探测器(Photo Detector，PD)的转换因子，B是调制带宽，Pr是接收的光功率，σ2是高斯噪声功率。该表达式在高信噪比条件下简单且精确，符合参考文献[24]的上界。需要注意的是，由于VLC系统的约束条件不同，与香农公式容量表达式本质上是一致的。

2.2 室内VLC小区构建

本部分提出一种新的用户聚类算法并给出一种新的AP关联算法。用户聚类的目标是最小化用户到光小区中心的距离以及最大化光小区之间的距离，既能确定最优聚类效果又能最大化不同小区边缘用户之间的距离，以减少小区间的干扰。

2.2.1 以用户为中心小区构建

本节中首先将用户分别分组到预定义的K个小区中，根据地理位置将其进行聚类，一方面使小区中所有用户到小区中心的距离尽可能小，有助于提高小区内的能源效率EE，另一方面使小区之间的距离尽可能远，有助于减少小区间的干扰。此场景下选取K-Means算法较为适合，该算法快速简单，其选取欧拉距离作为小区间相似性和距离判断准则，首先计算各用户到小区中心的距离平方和：

(4)

其中：xi，k表示第k个虚拟小区用户i的位置，μk是小区的中心。K-Means聚类算法能够实现用户聚类就是使目标函数J最小，这是一个反复迭代的过程，目标是实现小区内所有用户到小区中心的距离最小化。但是由于K-Means方法初始中心的选择是随机的，这会导致EE变差。而且该算法是在假设用户聚类数目K已知的前提下进行的，如果K值不准确会使聚类效果不佳，因此为了更加精确有效地反映小区之间的分离性以及小区内的紧密性，本部分引入BWP聚类有效指标[25]，BWP指标基于样本的几何结构，以数据集中的某个样本作为研究对象，对聚类效果进行有效性分析，目标是最小化用户到小区中心的距离以及最大化不同小区间用户的平均距离，来确定算法的最优聚类数K。

假设Nu给用户划分到K个用户聚类中，第M个用户聚类中的m用户的类间距离b(M，m)为该用户到其他每个聚类中用户平均值的最小值，类内距离w(M，m)为该用户对象到M类中其他用户对象距离的平均值。定义BWP指标为第M小区的第m个用户的聚类距离与其聚类离差聚类的比值：

(5)

其中：

(6)

(7)

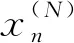
BWP指标反映了单个用户聚类的有效性，对于整体而言，可以通过计算所有用户聚类时BWP指标的平均值avgBWP(k)来分析总体聚类效果，其对应的最大值就是所需的最优聚类数kσ：

(8)

(9)

因此，算法1是本部分提出的聚类算法。

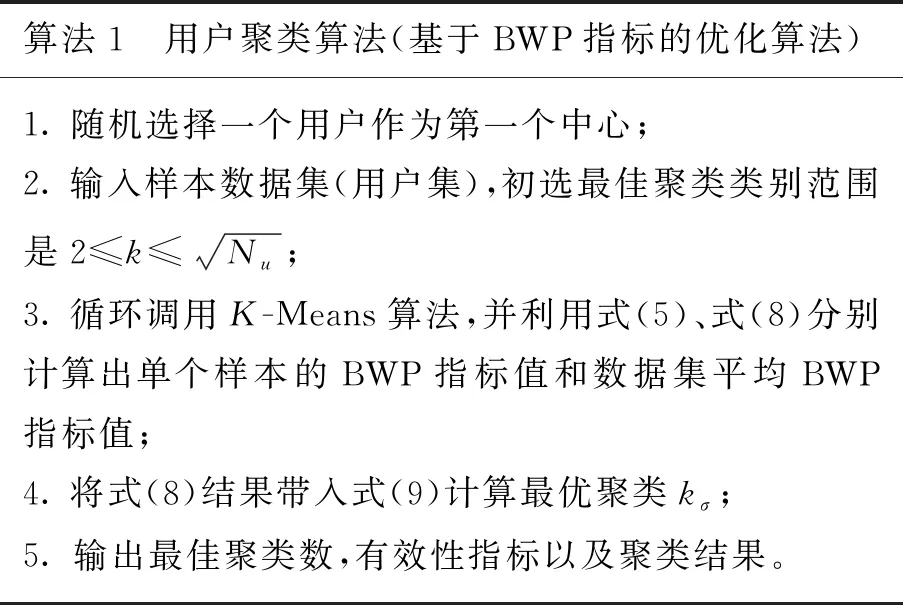
算法1 用户聚类算法(基于BWP指标的优化算法)1.随机选择一个用户作为第一个中心;2.输入样本数据集(用户集),初选最佳聚类类别范围是2≤k≤Nu;3.循环调用K-Means算法,并利用式(5)、式(8)分别计算出单个样本的BWP指标值和数据集平均BWP指标值;4.将式(8)结果带入式(9)计算最优聚类kσ;5. 输出最佳聚类数,有效性指标以及聚类结果。

BWP指标采用线性组合方式来平衡小区间距和小区内距离，并且能够处理小区间距离较小的用户集，由此使聚类效果更佳准确，从而得到准确度更高的聚类数目K。值得注意的是，该算法需要知道用户的位置，APs与用户建立连接，就可以使用光信道模型方程来推断用户之间的距离[26]，因此使用经典定位和跟踪算法来确定用户的位置[27-29]。因此，用户之间的相互距离以及任何一对AP-user的相互距离都是可以计算的，即用户的位置在AP端是已知的，可以在AP端就可以实现用户聚类。

2.2.2 AP关联用户聚类

用户聚类建立后，下面分三个步骤将APs与用户聚类关联在一起。

为了保证虚拟小区中APs数量不小于用户数目，首先计算APs与连接的用户之间的信道增益，并找到其中的最大值，从而利用最大值为每个用户选择最近的AP。此时有：

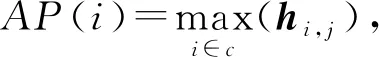
(10)

如果多个用户选择同一个AP，此AP选择最近的用户。直至每个用户成功选择唯一的AP。

每个AP在一定的范围内进行扩展，扩展过程中，对于用户聚类c，计算剩余每一个APs到该聚类c的用户平均信道增益，则有:

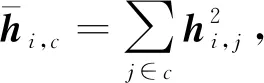
(11)

如果信道增益大于平均信道增益的APs与用户聚类相关联，小于等于平均信道增益的APs关闭。这样做的目的是为了提高本小区内的传输效率并减少对其他小区的干扰。

3 资源分配算法

本节要解决的问题是如何选择能增强EE的APs来为小区内用户分配功率。在第2节的虚拟小区形成之后，首先解决功率分配问题，然后提出一种联合解决功率分配和APs选择的算法。在K个虚拟小区中任意小区c中，假设AP发送给用户终端的数据向量为xc∈RNA，c×1，则接收到数据向量为yc=ρHcWcxc+nc，ρ是PD的响应度，Hc是信道矩阵，Wc表示预编码矩阵，nc代表高斯白噪声。

3.1 功率分配方案

本部分目标为保证虚拟小区中每个用户的公平性以及能够实现照明要求，在一定的QoS和最大可用功率约束下，使整个网络的能源效率EE最大化。EE函数定义为每消耗单位能量或功率所能提供的数据速率[30]，即：

(12)

其中：PT表示发射机消耗的功率，RT表示为总数据速率，即系统获取的性能，Pb表示维持发射机基本运行的功率，PS表示除发射功率之外其他电路系统所消耗的总功率，本文在公式EE中只考虑通信的损耗，故PS可忽略为零。对于每个光小区EE，假设为ηc，则整个网络中平均每个小区的EE为：

(13)

其中：

(14)

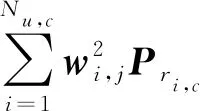
(15)

公式(15)通常使用集中化方式进行优化，而公式(13)支持分布式方法，简化一些处理，通过优化每个小区的平均EE，则能实现整个网络系统EE最优化，这样减少优化问题的复杂度，且能在每个小区中独立实现，则优化问题可以表述为：

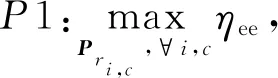
(16)

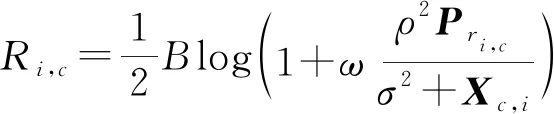
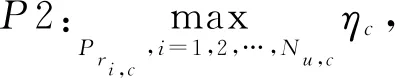
(17)

P2问题必须在每个小区中独立实现才能使得整个网络中各个小区的EE之和最大化。该问题不易解决，因为小区间干扰和功率分配是相互影响的。为了解决这个问题，首先假设在极端情况下解决这个问题，当所有APs都在以最大功率进行传输时，干扰也会达到最大值。P2目标函数是两个函数的比值，分子是凹函数，分母是线性函数，该问题是线性-凹分数规划问题。为解决该非凸问题，采用经典的参数化方法即Dinkelbach算法[32]来求解。该算法核心是将非凸问题转化为凸的子问题，求解子问题的最优解作为原问题的全局最优解.根据Dinkelbach算法将分数形式转化为减法形式的问题：

(18)

当且仅当满足式(19)的条件时，有式(2)成立：

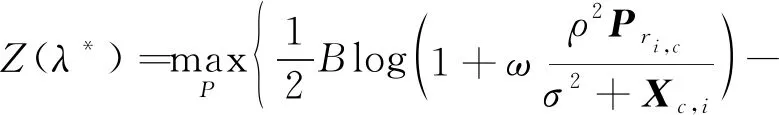
(19)

(20)

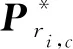
算法2 Dinkelbach算法1.初始化:设置误差精度δ,迭代索引t=1,初始化令λ(t-1)=0;2.在给定λ(t-1)的条件下,通过求解优化问题P3获得目前的解P(t-1)ri,c;3.While |Z(λ)|>δ,do4.t=t+1;5.基于P(t-1)ri,c计算λt;6.基于λt求解优化问题P3,直到获得最优解P*ri,c,终止;否则,λ=∑Nu,ci=112Blog1+ωρ2Pri,cσ2+Xc,i ∑NA,cj=1∑Nu,ci=1w2i,jPri,c+Pb,跳到步骤2,继续求解,直到Z(λ)≤δ为止;7.End while。

λ*求解后，P3的优化问题就是一个具有全局最优解的凹问题，凹问题具有很强的对偶性，可以利用对偶问题得到最优价。因此利用拉格朗日对偶性，P3中的问题的对偶性问题可以表示为：

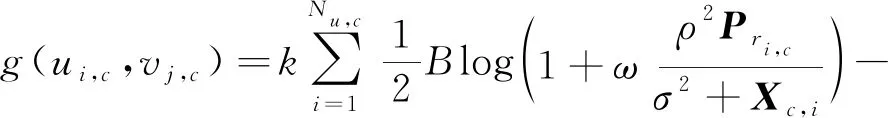
(21)

其中：ui，c是用户i数据速率约束的拉格朗日乘数，vj，c是总功率约束的拉格朗日乘数。则对偶域的优化问题可以表示为：

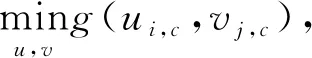
(22)

由于对偶域问题g(ui，c，vj，c)关于对偶变量ui，c，vj，c是线性关系，因此该问题是凸优化问题，可以使用次梯度法进行求解。次梯度法的关键是设置合适的步长，在次梯度法方向上拉格朗日乘数更新方法为：

(23)

(24)

其中：l表示迭代次数，yl表示拉格朗日乘数ui，c迭代的步长，zl表示拉格朗日乘数vj，c迭代的步长。只要步长设计的符合式(25)～式(26)的要求，就能够使用次梯度法将式(22)的解收敛直至最优：

(25)

(26)

在给定了ui，c，vj，c拉格朗日乘数值的基础上就可以得到原问题P3的最优解，根据Karush-Kuhn-Tucker(KKT)条件可知[33]：

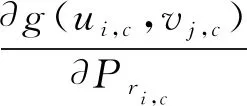
(27)

可以得到最优功率分配结果为：

(28)

3.3 联合功率分配与APs选择

本节中，在最优功率分配策略下优化参与通信的APs，一方面增强小区内EE，另一方面尽量减少小区间的干扰。显然，如果增加小区中APs的数量将增强该小区EE，但是同时也增强了其他小区的区间干扰。因此本部分提出一种新的AP关联技术，在光小区中，根据功率分配优化AP的选择，把APs分配给小区中的用户，打开带来增益的AP，关闭带来干扰的AP，目标是对于每个AP选择可能服务的关联用户或者尽可能增加EE的最佳虚拟小区。

AP的选择高度依赖于所分配的功率，因为用户分配功率的同时也在AP上传输功率，因此AP的选择和功率分配问题是相互关联的，本部分提出一种迭代算法，找到两者的联合解。首先优化参与通信的APs以最小化小区间干扰。在最优功率分配策略下，当增加传输中参与APs时，只要忽略小区间干扰，EE就会增强。因此，先将APs进行分类：对所有用户没有连接的APs(关闭)；对本小区关联用户有连接但对其他小区的用户没有连接的APs(打开)；与本小区用户连接但对其它小区用户也有连接的APs。对于上述3类，第3类APs需要仔细选择打开或者关闭。因此，针对第3类APs，本部分引入一个权值，利用该权值来决定AP是否参与通信：

(29)

ξc，i值越大，说明用户i从APs接收的有用信号远大于接收的干扰，反之亦然。下面给出算法3交替求解功率分配与APs选择，直到收敛为止。

算法3 联合AP选择和功率分配,实现EE最大化1.指定所有APs,根据计算得到的ξc,i值进行排序,假设R为干扰APs的个数;2.对于i=1:R;3.更改AP i的状态,如果AP i是状态on,则关闭它,反之亦然,同时保持满足每个小区中活动AP数量大于用户数量;4.执行功率分配,并检查EE是否得到改善,如果没有,返回AP之前的状态;5.循环直到收敛。

算法3中对APs通过排序进行取舍，一方面能保证小区内APs的数量高于用户数量，另一方面也能明显提升收敛速度。执行该算法时需要注意在步骤4，要保证小区中的干扰完全消除，如果APs数量小于用户数，则无法保证。此外，由于本文是假设用户数量低于APs数量，通过对APs的排序可以避免有些小区用户数量大于APs，有些小区只有少数用户，因此对APs建立度量值也可以避免或者减轻VLC系统的负载不平衡，并能尽可能减少小区间干扰。

算法3保证收敛，随着步骤3中AP状态的每一次改变，EE要么改进，要么保持不变。此外，随着迭代次数的增加，该方法可以保证得到最优解。在每次迭代中，所提算法通过对每个AP执行功率分配问题来测试所有的干扰AP，这意味着算法3尝试了所有可能的解决方案来得到最好的解。重复测试干扰AP的原因是APi的最佳状态(开或关)取决于所有其他干扰AP的给定状态，特别是靠近APi的干扰AP。

3.4 复杂度分析

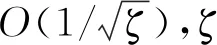
4 仿 真

本节模拟一个室内可见光通信系统，室内用户数目少于Aps数量，在保证照明的前提下评估上节提出的节能方案。假设室内长12 m，宽12 m，高3 m，64组LED阵列，20个用户。如图1所示，笛卡尔坐标系统原点为天花板中心，用于指定用户终端和LED阵列的位置，假设所有的用户在同一个接收平面上，高为0.75 m。使用蒙特卡洛仿真评估本算法的性能，在每次迭代过程中，生成一个均匀的随机用户分布。仿真参数如表1所示。

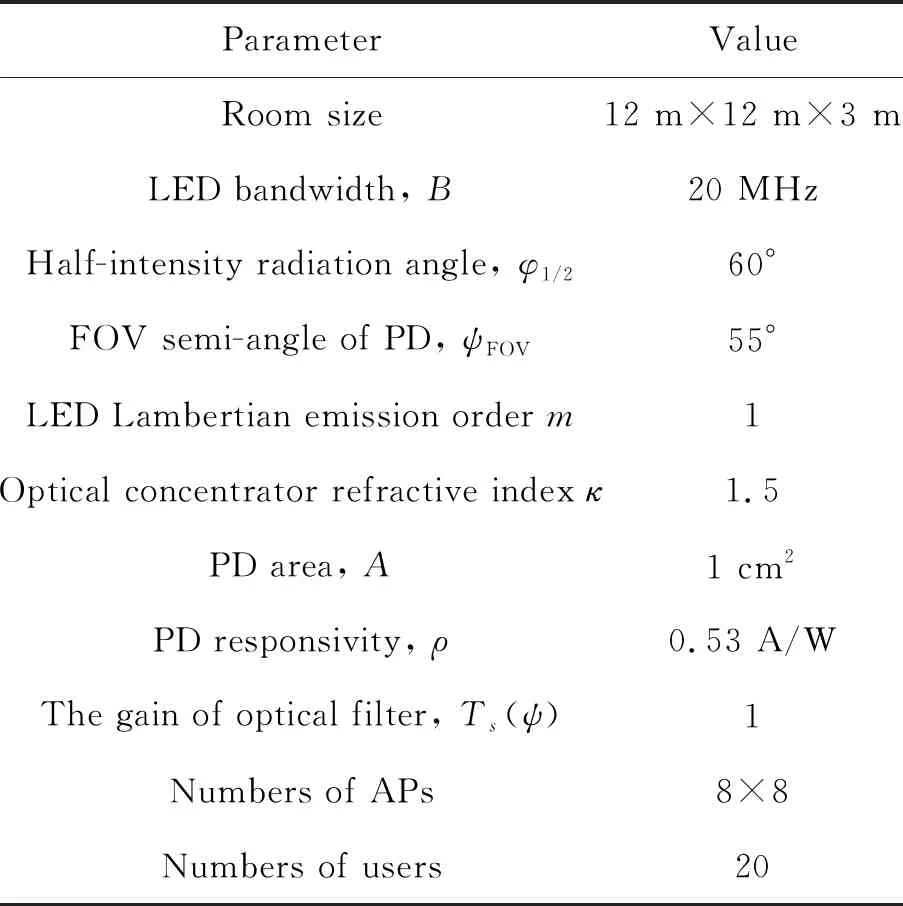
表1 系统仿真参数Tab.1 System parameter used for simulation

图2描述了能量效率与迭代次数的关系，从图中可以看出，当所有APs参与通信时，随着迭代次数的增加EE也随之增加，并且随着迭代次数的增加，增加的速率变小，这是因为每次迭代，都需要在每个虚拟小区中实现功率分配的问题，这意味着增加迭代的次数会增加复杂性，但是会显著提高性能。从图2中也可以看出了本算法的收敛性，算法3需要最多三次迭代来收敛，系统的能量效率达到最大，系统性能也趋于稳定，而且收敛所需的迭代次数不依赖于系统的虚拟小区数量。此外可以看到，只有前两次迭代在系统的EE方面产生了显著改进，特别是在虚拟小区数量K较大的情况下。与K-means++聚类算法相比，明显可以看出本算法的优越性。

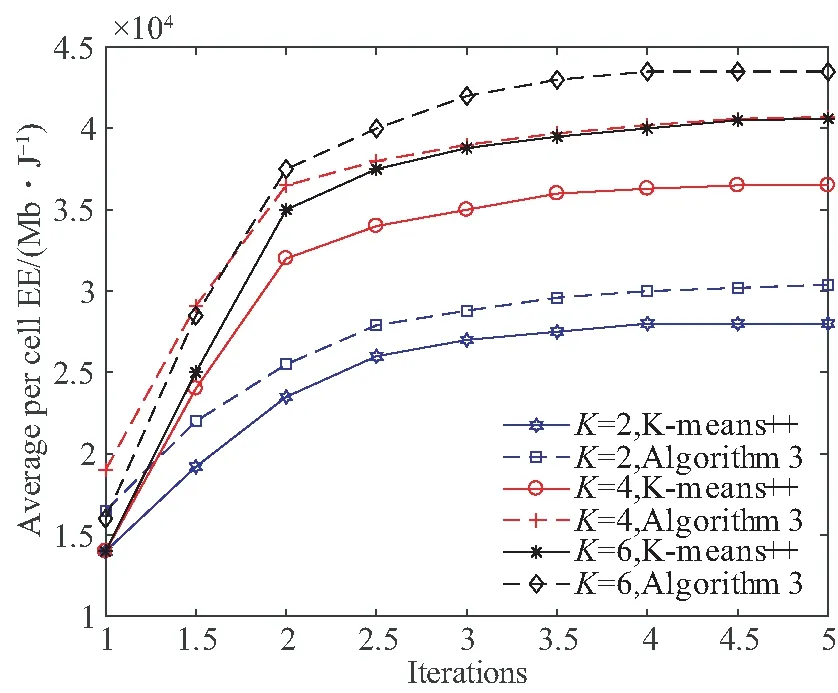
图2 不同虚拟小区数量(K)和不同用户小区下能源效率与迭代次数的关系

图3描述了平均EE与小区数目的关系，与所有AP参与传输相比，算法3中的EE有了显著改进。理论上来说，当小区数增加时小区间干扰也会增加会导致EE降低。但是，图3显示小区平均EE随着小区数量的增加而增加然后又少量减少，这说明当小区数量增加时，还有一个因素可以帮助提高小区的平均EE。这个因素是小区内的用户数量，随着小区数量的增加，每个小区下的平均用户数量会减少，意味着随着小区数量的增加，每个小区所需的传输功率降低，从而提高了每个小区的平均EE。当小区间干扰较小时，即小区数目较少或者FOV较小时，这一因素影响会比较大。

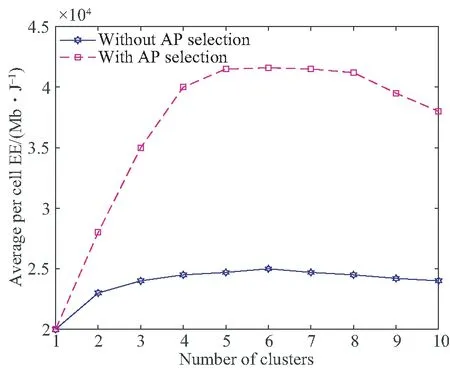
图3 比较算法3对AP进行选择及所有APs参与通信时的EE

图4表明GEE随着小区数量的增加而减少，这是因为整个系统中用户的数量对GEE有较大的影响。需要注意的是，本文所提算法是在输出功率分配的基础上，针对最大化平均每个小区的平均EE而建立的。当增加小区数量时，增加的干扰较小，这是主要因素，导致每个小区平均EE随着小区数量的增加而增加。GEE的计算可以通过公式(15)来计算，GEE减少，原因从小区平均EE与GEE的定义可以推导出。如图所示，算法3在GEE计算方面有了显著改进。而且本文所提出的用户聚类算法也优于K-means++算法。

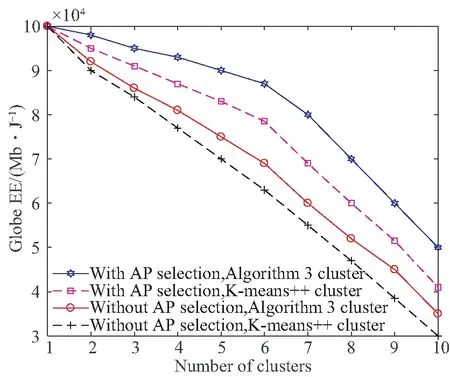
图4 比较算法3对AP进行选择及所有APs参与通信时的GEE

图5反映了基本运行功率与GEE之间的关系，对参考文献[16]与本文算法3做了对比。从图5可以看出，基本运行功率增高，GEE会随之降低，这是因为随着基本运行功率的增大，如果维持GEE效率，发射机需要的传输时间也会增加，反过来降低了GEE。

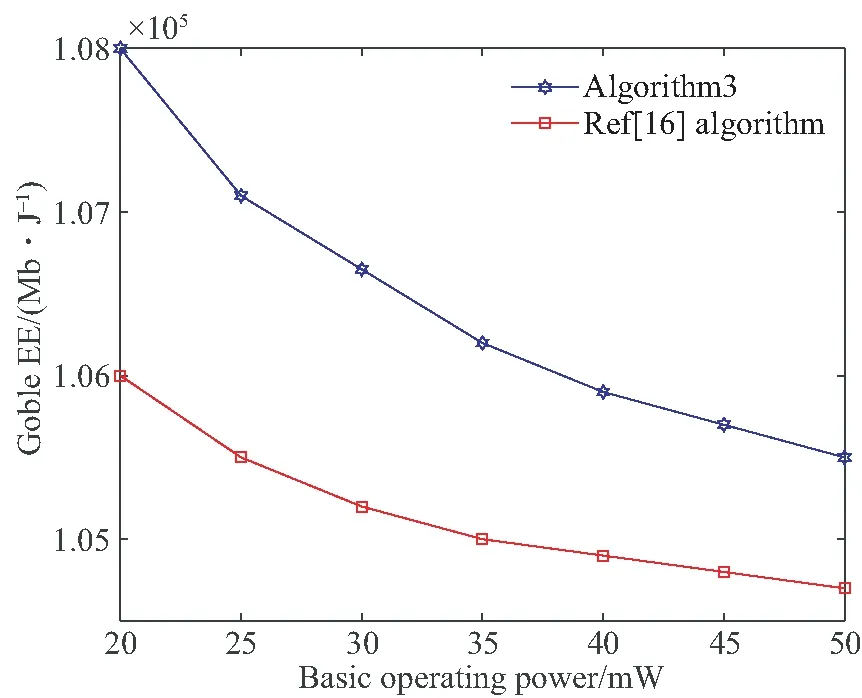
图5 基本运行功率与GEE的关系Fig.5 Relationship between basic operating power and Goble EE

在图6中，将本文APs关联算法与参考文献[16]中提出的算法进行了比较。采用相同的用户聚类算法、相同的功率分配算法，并进行了200次蒙特卡罗仿真。本研究中是联合处理功率分配问题和AP关联问题，参考文献[16]中是分别解决这两个问题。此外，根据每个AP对小区用户的平均信道增益，为每个AP建立了一个权值标准，目的是选择最佳的小区服务并减少小区间的干扰。然而参考文献[16]中提出的算法可以简单解释为，为每个用户选择目标AP后，其余的APs扩展在一定范围。如果APi有多个小区满足此条件，则必须关闭此AP以减少干扰。这种方法的缺点是，增加或减少范围可能打开有害APs和关闭有帮助的，因为它只取决于距离而不受不同因素影响，比如接收机FoV，发射机覆盖等。因此，如图6所示，本文算法在光小区平均EE方面明显优于参考文献[16]算法。

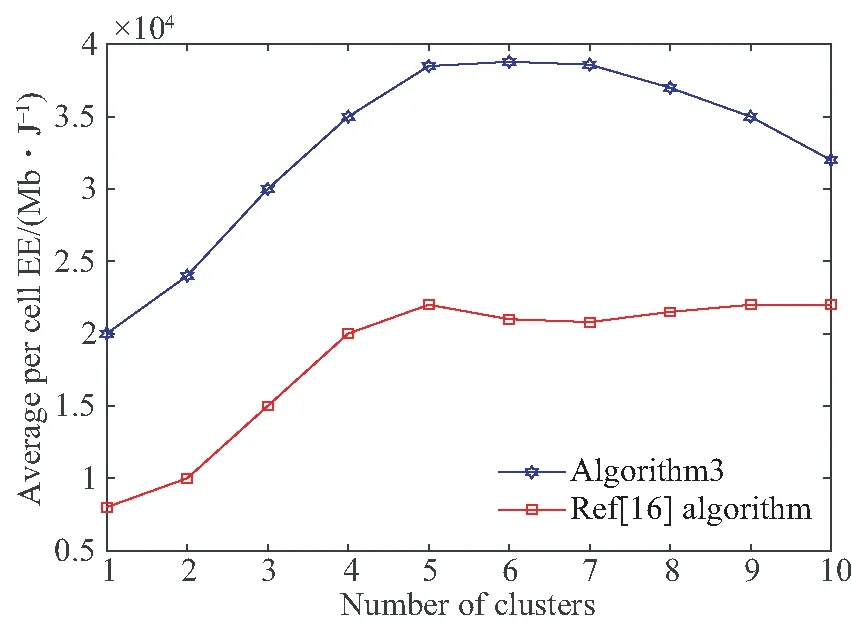
图6 本文算法与参考文献[16]算法在平均EE方面比较

5 结 论

本文基于以用户为中心的可见光网络，设计了一种联合功率分配和关联APs选择的高效节能网络，文中提出一种基于BWP聚类指标的算法，最小化用户到小区中心的距离以及最大化不同小区间用户的平均距离，找到最佳聚类数目，在APs与用户聚类关联时引入了新的度量值，进一步减少小区间干扰。此外，建立以最大化系统能效为目标的分式优化问题，基于Dinkelbach算法以及拉格朗日对偶域梯度求解方法进行求解，获得了可见光系统中高能效资源分配方案，并对计算复杂度进行了分析。仿真结果表明，考虑小区间干扰问题，设计合理的用户聚类算法，根据分配的功率进一步选择服务的APs，能显著改善EE最大化问题。